KONDANSATÖRLER
Herhangi bir yolla negatif olarak yüklenmiş B levhasını bir iletken telle yüksüz bir
elektroskopun topuzuna birleştirdiğimizde B levhasındaki yükün bir kısmı her ikisinin de
potansiyelleri eşit oluncaya kadar elektroskopa geçer ve yüklenen elektroskopun yaprakları açılır.
Başlangıçta yüksüz olan bu A metal levhasını, B metal levhasına yaklaştırdıkça, aradaki uzaklığa bağlı
olarak elektroskoptaki yaprakların açıldığı biraz azalırken A metal levhası da indüksiyonla B’nin
yüküne eşit ve pozitif olarak yüklenir. Bunun sonucu olarak B levhasının potansiyeli azalmış ve yük
alma özelliği artmıştır.Levhalar arasındaki d uzaklığı değiştirmeden areadaki hava ortamı yerine
mika, cam gibi yalıtkan ortamlar konulunca elektroskopun yapraklarının biraz daha kapandığı
görülür.O halde levhaların yük alma özelliği levhalar arasındaki yalıtkan ortamın cinsine bağlı olarak
değişir. Böyle, aralarında yalıtkan bir ortam bulunan iki iletkenden meydana gelen sisteme
kondansatör adı verilir. Kondansatörler elektrik depo etmeye yarayan düzeneklerdir. İletken
levhalara kondansatörlerin armatürleri denir.Armatürler, bir üretecin kutuplarına bağlanırsa,
kondansatör yüklenmiş olur. Üretecin negatif kutbuna bağlanan armatür –q, pozitif kutbuna
bağlanan armatür ise +q yükü kazanır. Kondansatörün yükü denildiğinde armatürlerden biri
üzerindeki yük miktarı anlaşılmalıdır. Kondansatörler belli bir kapasitenin üzerinde yükle yüklenirse,
aradaki dielektrik madde yalıtkanlığını kaybederek iletken hale gelebilir. Kondansatörler kıvılcım
patlaması ile boşalabilir.
Armatürler arasındaki potansiyel farkı V, yükü q olan bir kondasatörün sığası, C= q / V
bağıntısından hesaplanır. Armatürleri düzlem levhalar şeklinde olan kondansatörlere, düzlem
kondansatör adı verilir.
Bir düzlem kondasatörü armatürlerinden birinin yüzölçümü (A), yalıtkan tabaka kalınlığı(d),
dielektrik katsayısı () ise kondansatörün sığası;
A
C= ------- bağıntısından hesaplanır.
d
Armatürlerin birinin yüzölçümü (A), dielektrik kalınlığı (d) ve dielektrik katsayısı () C=
(A/d) olur.
Düzlem kondasatörünün sığası ;
1. Armatürlerin yüz ölçümü (A) ile doğru orantılıdır
2. Levhalar arası uzaklık (d) yani dielektrik kalınlığı ile ters orantılıdır.
3. Dielektrik sabiti () ile doğru orantılıdır.
Kondansatörlerde yalıtkan madde olarak hava,cam,ebonit,mika..... vb kullanılır. Düzlem
kondansatörlerde armatür yüzey alanı , dielektrik sabiti, armatürler arası uzaklık ve sığa ile ilgili
semboller ve birimler Tabloda verilmiştir.
1
Nicelik
Sembol
Birim
Armatürler Arası
Uzaklık
d
m
Ortamın Dielektrik
Sabiti
F/m
Armatürlerden birinin yüzey
alanı
A
m²
Sığa
C
F
Kondansatörler genel olarak elektrostatik deneylerde alternatif akım radyo ve televizyon
devrelerinde kullanılır.
Kondansatörlerin Bağlanması
Birden fazla kondansatörün oluşturduğu sistemin sığasına eş değer sığa denir.
Kondansatörlerin Seri Bağlanması
Kondansatörlerin birinin negatif armatürü diğerinin pozitif armatürüne gelecek şekilde art
arda
bağlanmasına kondansatörlerin seri bağlanması denir.
Seri bağlı kondansatörlerin yükleri birbirine eşittir. Bu da sistemin eş değer yüküdür.
Seri bağlı kondasatörlerin uçları arasındaki potansiyel farkların toplamı , sistemin
potansiyeline eşittir.
Eğer değerleri yerine yazarsak ;
Formülü ile ikiden fazla kondansatörlerin seri bağlanması
sonucu oluşan C değerini buluruz.
Kondansatörlerin Paralel Bağlanması
İki veya daha fazla kondansatörün negatif işaretli armatürlerinin bir noktaya , pozitif yüklü
armatürlerinin diğer bir noktaya bağlanmasına kondansatörlerin paralel bağlanması denir.
2
Eğer sistemde ikiden fazla kondansatör paralel bağlanırsa eş değer sığa C= C1+C2+C3+ ....+ Cn
Sistemin eş değer yükü her bir kondansatörün ayrı ayrı sahip olduğu yüklerin toplamına eşittir.
qt = q1 + q2
Kondansatörlerin uçları arasındaki potansiyel farkları aynı olup sistemin potansiyeline eşittir.
V = V1 + V2 ..
ÖRNEK :
Şekilde verilen seri bağlı kondansatörlerin sığaları C= 8uF
Ve C=12uF ise devrenin ;
a) Eş değer sığasını
b) Eş değer yükünü
c) Her bir kondansatörün yükünü
d) Her bir kondansatörün potansiyelini bulalım.
ÇÖZÜM :
a)
C = 4uF
b) q= C.V = 4. 24 = 96uC
c) Seri bağlı kondansatörlerin yükleri birbirine eşit olıp o da sistemin yüküne eşit olacağından q =
96uC olur.
d) V + 16 = 24 V= 8 volt
Yüklü Bir Kondansatörün Enerjisi
Yüksüz bir kodansatörün levhaları arasındaki potansiyel farkı sıfırdır. Düzgün olarak
kondansatöre yük verilirse doğru orantılı olarak potansiyel enerjisi
artar. Yük kazanan kondansatörün potansiyeli V olur. Buna göre
ortalama potansiyeli de Vort = V / 2 ile bulunur. Kondansatör
yüklenirken elektriksel kuvvetlere karşı yapılan iş kadar bir enerji
kazanacağından bu enerji ;
İfadeleri ile bulunur.
Grafikte yükün potansiyel ile değişimi gösterilmiştir. Grafikte taralı alan
kondansatörün elektriksel potansiyel enerjisini verir. Bu enerji de kondansatörü yüklemek için
yapılan işe eşittir.
ÖRNEK :
Sığası 4uF olan düzlem kondansatörün levhaları arasındaki potansiyel farkı 15 volttur.
Kondansatörün yükü ve enerjisinin ne olacağını bulalım.
ÇÖZÜM :
C=4uF q= C.v= 0,00006
W= 1 / 2 (0,000004) 15 15 W= 0,00045 J olur.
ÖRNEK : Bir fabrika hangarında 220 V / 40W lık 200 adet flouresans lamba aydınlatma için
kullanılacaktır. Her bir lambanın balast gücü 8W dır. A) cos = 0,4 b) cos = 1 iken ana hattan
geçen akımları ayrı ayrı bulunuz.
ÇÖZÜM :
a) Her bir lambanın balastı ile birlikte güç çekişi 48 W 200 adet lamba için etkin güç 200x48 =
9600W olur.
Cos = 0,4 için görünen güç ;
3
S = P / cos = 9600 / 0,4 = 24000VA = 24 kVA
220 V gerilim altında geçen akım :
I = S / U = 24000 / 220 = 109 A
b) cos = 1
S= P / cos = 9600 / 1 = 9600VA I = S / U = 9600 / 220 = 43,6 A
Buradan cos = 0,4 iken cos = 1’e değinle en az ından 2,5 misli çapta bir ana hat kablosuna
gereksinileceği çıkartılabilir. Tepkin gücün görünen güce oranı tepkin faktörü ya da reaktif faktör
olarak tanımlanır. Sinüzoideal alternatif akımda reaktif faktör sin ye eşittir.
KAPASİTE
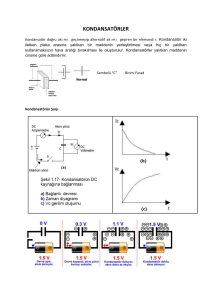
1. DOĞRU AKIM DEVRESİNDE KONDANSATÖR
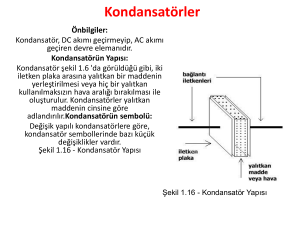
Esas olarak bir kondansatör iki metal plaka ve bu plakalar
arasında dielektrik diye anılan bir yalıtkan maddeden oluşur.
Şekilde görülen devre modelinde bir kondansatör, devredeki
komitatör şalteriyle doğru akım üreten bir gerilim kaynağına (G)
bağlanabilecek durumdadır. Kondansatöre seri olarak ibresi skala
ortasında duran bir mikroampermetre (uA) bağlıdır.
Komitatör şalteri önce şarj yönünde çevrilip akım devresi
kapatıldığında mikroampermetre ibresinin kısa bir süre saptığı ve
sonra sıfıra döndüğü görülecektir. Şayet komitatör bu durumda deşarj yönüne çevrilir ise , bu
kez ibrenin aksi yöne saptığı ve yine sıfıra döndüğü izlenecektir.
Kondansatörün şarj anında kısa bir süre şarj akımı geçer. Bu sürenin bitiminde
kondansatör doğru akımı geçirmez.
Kondansatörler Doğu Akımı Engeller .
Şarj anında gerilim kaynağı bir emme basma tulumba gib çalışarak bir plakadan elektronları
emer ve bunları diğer plakaya pompalar. Bu nedenle bir plakada elektron azlığı , diğer plakada
elektron fazlalığı ortaya çıkar. Bunun sonucu plakalar arasında uygulanan gerilimin aksi yönünde bir
gerilim oluşur. Bu gerilimin nedeni ile deşarj anında kondansatörden şarj akımının aksi yönünde bir
deşarj akımı ya da dengeler akımı akar.
Kondansatörler Elektrik Yüklerini Depolar.
Bir kondansatörün elektrik yükü depolama niteliği Elektriksel Kapasite olarak bilinir.
Kapasitenin birimi Farad’tır. Farad birimi çok büyük olduğundan uygulamada yalnız azkatları
kullanılır. Bunlar mikrofarad, nanofarad , ve piko farad’dır. Şekil için anılan sınama bu kez, önce iki
misli gerilim uygulayarak ve sonra iki misli kapasitede başka bir kondansatöre koyarak
tekrarlandığında ampermetre sapışının ikişer misli daha büyüdüğü görülecektir.
Kondansatörün kapasitesi ve uygulanan gerilim ne denli büyük olursa depolanan elektrik yükü
o değin büyük olur.
Q=CxU
Q= Yük , C= Kapasite , U=Gerilim
Elektirk yükünün birimi Coulomb’dur. Ancak uygulamada Amper saniye (As) birimi de
kullanılır.
1 Coulomb = 1 Amper saniye
ÖRNEK :
Kapasitesi 50uF olan bir kondansatörün plakaları arasında 220 V luk bir doğru gerilim ölçülmüştür.
Plakalara depolanan Elektrik yükünü bulunuz.
ÇÖZÜM :
Q = C . U = 0,00005 x 220 = 0 ,011 As
4
1. Kapasitenin Hesabı :
Kondansatörlerin kapasitesini ölçen aletlere kapasitörmetre denir. Bu değin bir ölçü aletiyle
örneğin iki levha karşı karşıya getirilerek ;
a) Levha yüzeyleri büyütülmek ,
b) Levhalar birbirine yaklaştırılmak ,
c)
ve levhalar arasına çeşitli yalıtkan maddeler
sokulmak suretiyle ölçümler yapılmıştır. Elde edilen
sonuçlara göre a-) , b-) ve c-) de sıralanan ögelerin
kondansatörün kapasitesi üzeinde tek tek etki ettiği
saptanmıştır. Nitekim ya da plaka yüzeylerinin
büyütülmesi, transfer edilen elektronlara daha büyük
yerleşme yüzeyi sağlar. Plakalar arası uzaklık küçüldükçe
plakalar üstündeki farklı yükler daha çok birbirini
çekerler. Bundan dolayı uygulanmış gerilim daha çok
sayıda elektrik yükünü kondansatör içine sürükliyecektir.
Buna göre dielektirikin molekülleri kondansatör plakaları arasında oluşan yapısı , molekülün bir
yanında pozitif yükler , diğer yanında negatif yükler ağır basacak şekildedir. Bu yapıda bir molekül
moleküler dipol olarak tanımlanır. Elektrik alanı içinde moleküller dipoller birbirini hizalar. Bu oluşum
dielektriki Polarizasyon olarak ya da Tesirli elektiriklenme olarak adlandırılır.
Bu polarizasyon nedeni ile yalıtkan maddenin cinsine göre kondansatör plakalarında bulunan
elektrik yüklerinin belirli bir miktarı nötr durumuna geçer. Bundan dolayı kondansatör plakaları ,
plakalar arasındaki eski gerilim durumuna erişilinceye kadar, daha çok sayıda elektrik yükünü kabul
edebilecektir. Daha çok sayıda elektrik yükünün kabul edilmesi kapasitenin büyümesi sonucunu
getirir.
Bir kondasatörün plakaları arasında hava yerine başka bir yalıtkan maddenin kullanılmasıyla,
kapasitenin ne kadar büyüceğini veren sayı o yalıtkan maddenin dielektrik katsayısı (=eplison)
olarak anılır.
Bir kondansatörde plaka yüzeyleri ile dielektrik katsayısı ne denli büyük ve plakalar arası
uzaklık ne denli küçük olursa, kapasitesi o değin büyük olur .
C= Kapasite (pF)
A= Plak yüzeyi (cm²)
d= Plakalar arası uzaklık (cm)
= Dielektrik katsayısı
Formülde görülen 0.0085 katsayısı elektriki alan sabitesidir (o)
ÖRNEK :
Bir kondansatörde karşılıklı plakaların birbirini gören yüzeyi 30 cm² dir. Plakalar arası uzaklık 0,05
mm olduğuna göre, dielektrik a) hava b) Fiber olduğu halde bu kondansatörün kapasitesini
hesaplayınız.
ÇÖZÜM :
a) C= 0,0885 . 1 . 30/0,005 = 53pF
b) C = 0,0885 . 4 . 30 / 0,05 = 212pF
2. Zaman Sabitesi
Bu deneyde daha önceki deneylerden farklı olarak , kondansatöre bir direnç seri bağlanıp
tekrarlanmıştır.
Seri direncin değeri büyütüldükçe ampermetre ibresinin şarj anında daha yavaş ve daha uzun
süre saptığı izlenecektir. Kondansatör kapasitesinin büyütülmesiyle de aynı sonucun ortaya çıktığı
görülecektir.Bir kondansatörde , kapasitesiye ve öndirencine bağlı olarak şarj zaman süresinin
ölçüsü zaman sabitesidir.
5
(tau) Bir kondansörün uygulanan gerilimin % 63 ‘ne şarj edebilmesi için ne kadar süre
gereksindiğini zaman sabitesini verir.
= Zaman sabitesi
C = Kapasite
R = Direnç
= C . R
Her kondansatör 5. süre sonra uygulanan gerileme yaklaşık tam şarj olur.
ÖRNEK :
Kapasitesi 10uF olan bir kondansatöre 100 k æ luk bir direç seri bağlanmıştır. Kondansatörün tam
şarj olabilmesi için geçecek süre nedir.
ÇÖZÜM :
Şarj zamanı = 5 . = 5 . C . R = 5 . 10 . 0.000001 . 100000 = 5saniye
2.
ELEKTRİK ALANI :
Şekilde görüldüğü gibi yüklü 2 kondansatör plakası arasında
ince ipek iplikle kehribar bir bilya asılmıştır. Bilya kısa bir süre
plakalardan birine değdirilirse, bu plakadan itildiği ve karşı plakaya
çekildiği ; karşı plakaya değdiğinde aynı şekilde ilk plakaya doğru
itildiği ve bu hareketin bir sarkaç gibi bir süre gittiği izlenecektir.
Bilya örneğin negatif plakaya değdiğinde, buradan elektron
olarak plaka potansiyelinde yüklenir. Aynı yükler birbirini
iteceğinden bu plakadan itilir. İtme hareketinin eylemsizliği ile karşı
plakaya sürülür. Karşı plakaya vardığında taşıdığı elektronları,
elektron azlığı olan pozitif plakaya transfer ederek, kendisi de
elektron az yani pozitif duruma geçer.
Bunun sonucu pozitif plakadan itilerek , salınım hareketi iki plaka arasında bir süre gider. Bu
salınım hareketi iki plaka arasında yükler dengelendiği zaman durur.
Bilyanın bu değin bir salınım hareketi plakalar arasında bir kuvvetin varlığını ortaya
koymaktadır. Bir mıknatısın kutupları arasında olduğu gibi kondansatör plakaları arasında da bir alan
vardır, ancak bu alan manyetik alana farkla elektrik alanı olarak tanımlanır.
Elektrik alanı, manyetik alan içinde
demir tozlarına benzer şekilde , örneğin cam
pamuğu , alçı tozu ve ince kum tanecikleri gibi
izole cisimlerle görülür duruma getirebilir.
Elektrik alanı içine serpilmiş bu cins izole
tozlar alan etkisi altında arka arkaya dizilerek
çizgiler
oluştururlar.
Yüklenmiş
metal
parçacıklarında elektrik alan çizgileri kutup
yüzeylerine daima dik girecek ya da çıkacak
şekilde tertiplenirler.
Elektrik alanı yalıtkan cisimler içinde
oluşur. Örneğin iki iletken arasındaki havayı
verebiliriz. Yüklenmiş iki paralel plaka arasında bu alan tek tip şiddeetlidir, yani homojendir. Bu
nedenle elektrik alan şiddeti iki plaka arasında sabit kalır.Elektrik alanını doğuran neden elektrik
gerilimidir. Hiçbir akım geçmiyecek şekilde plakalara olan bağlantılar çıkartılırsa bile
kondansatördeki gerilim seviyesi ve bununla birlikte elektrik alanı yerinde kalır. Plakalar arasındaki
elektrik alanı , plakalar arası uzaklık oranında uygulanmış gerilime eşittir.
6
E = Elektrik alanı (V/cm)
U = Gerilim (V)
d = Uzaklık (cm)
Elektrik geriliminin bulunduğu her yerde elektrik alanı vardır.
Elektrik alan çizgileri manyetik alan çizgilerine karşın kapalı devre çizgileri değildir.
Çizgilerin yönü, örneğin iki kondansatör plakası arasında pozitif plakadan negatif plakaya doğrudur.
Alan çizgileri pozitif yükten başlarlar, negatif yükte biterler. Alan çizgilerinin tek tip şiddetli
olduğu alanlar üniform alan olarak anılır. Elektrik alanının kurulması için elektrik enerjisi gereklidir.
Örneğin bir kondansatörün şarjından sonra bu enerji elektrik alanı içinde depolanır. Deşaj anında da
alan içinde depolanmış enerji tekrar serbest hale geçer.
Bir yalıtkan malzemenin elektrik gerilimine karşı
dayanımı elektrik alan şiddetine bağlıdır. Örneğin kuru
hava 30 000V/cm lik bir alan şiddetinde dayanımını
yitirir ve bu oluşum için yalıtkan delinmesi deyimi
kullanılır. Yalıtkan malzemelerinin elektrik alan
şiddetlerine karşı dayanımları dielektrik dayanımı olarak
tanınmaktadır.
Yalıtkan bir maddenin delinmesi ya da dielektrik
dayanımını yitirmesi, onun bir deyimle iletken haline
geçmesinden başka bir şey değildir. Bir yalıtkanın
iletken hale geçmesi suretiyle oluşan elektrik akımı
elektrik arkı yanıi bir kıvılcım şeklinde ortaya çıkar.
Bir yüksek gerlilim – zincir izolatöründe ortaya çıkan bu değin bir elektrik arkı
görülmektedir.Yalıtkanların dielektrik dayanımları ortamın tozlu, kuru, nemli olmasına ve ısısına göre
değişir. Örneğin nemli bir havanın dielektrik dayanımı düşer.
Bazı durumlarda elektrik alanı elektrik arkı oluşturmadan da ortamın dielektrik dayanımını
delebilmektedir. Örneğin çok yüksek gerilim ileten hatların hemen yakınlarındaki hava iyonize olur
ve bu nedenle hattın etrafında oluşan ışıklı tabaka karanlıkta görülebilir. Bu oluşuma korona olayı
denilir. Korona olayının nedeni, hattın hemen yanındaki bir noktada elektrik alan şiddetinin havanım
dielektrik dayanımından daha büyük olmasıdır. Ancak teller arasındaki her noktada alan şiddeti bu
kadar büyük olmadığından bir elektrik arkı oluşmamaktadır.
Yer altı kablolarında ve kondasatörlerde dielektrik dayanımı söz konusudur. Bu nedenle
yalıtkan cisimler işletme gerilimine göre güvenlikli seçilmelidir.
Kondansatörler üzerinde verilmiş olan gerilimler güvenlikli seçilmiş işletme gerilimlerinidr.
Bir kondansatörün işletme gerilimi o kondansatörün dielektrik dayanımı ve plakalar arası uzaklığına
göre hesaplanmış en büyük dayanım geriliminin en az yarısıdır.
Bu nedenler kondansatörler üzerinde yazılı işletme gerilimlerinin en az iki misli geçilmedikçe
kolay kolay delinmezler.
3. KONDANSATÖR YAPI ŞEKİLLERİ
1.SABİT KONDANSATÖRLER :
a) Kağıtlı Kondansatör :
Bu kondansatörler iki adet metal tabakandan oluşmuş i letken yüzeylerden meydana
gelmiştir. Metal tabakalar arasında dielektrik olarak emprenye edilmiş (öz suyu çekilmiş) izole
kağıt kullanılmaktadır.
7
Yerden kazanç sağlamak amacı ile metal tabakalar rulo şeklinde üstüste sarılmıştır. Sarma
anında tabakalar arası kısa devreyi engellemek amacıyla, ikinci bir kat izole kağıt kullanılır. Sarılmış
halde kondansatör bir borucuk ya da alüminyum bir kap içerisine sokulur ve zift dökülerek ağız
kısımları kapatılır. Aynı kap içine bu değin sarılmış birkaç kondansatör konulabilmektedir. Rutubetli
ortamlarda kullanılacak kağıtlı kondansatörler üzerine ikinci bir izole kılıf geçirilir.
Bugünkü standartlara göre kondansatörler üzerinde şu veriler yazılı olmalıdır.
Anma Kapasitesi (Örneğin 10uF )
Tolerans (Örneğin (+) veya (-) %10 ; bir tolerans değeri yazılı değilse (+) veya (-) %20
anlaşılacaktır )
Anma Gerilimi (Örneğin 500V) ; Bir kondansatörün anma gerilimi, o kondansatöre 40C lik bir
çevre ısısında uygulanacak gerilim değerdir; alternatif gerilim yazılı ise, bundan etkin gerilim
anlaşılacaktır.
Yapı Şekli (Örneğin : Kondansatör uçları ile tabakalar arasındaki bağlantı şekli) Bu amaç için
çeşitli simgeler kullanılır. Örneğin : Alman standartlarına göre hazırlanan anlamları şöyledir:
<<k>> işareti : Kaynak lehim ya da metal püskürtme yöntemleri ile oluşturulmuş yapı şekli,
<<d>> işareti : Sarsıntıya dayanıklı çok bağlantılı yapı şekli
işaretsiz
: Pres bağlantı yapı şekli
b ) Metal – kağıt kondansatör : (MP-kondansatör)
Kağıttan şeritler vakumda (havasız ortam) örneğin,
çinko buharına tutularak üzerleri ince bir metal tabaka ile
kaplanır. Bu türde iki şerit üst üste sarılmak suretiyle MP –
kondansatörü elde edilir. Çok katlı yapı şekillerinde metal
tabakalı şeritler arasına izole tabakalar konulmuştur. Bu
şekilde oluşturulan metal tabakalı şeritler karşı karşıya
gelecek şekilde yerleştirilir ve sargıların alın kısımlarına
metal püskürtülür. Püskürtülen metal tabakası metal kaplama
ile uçlar arasında bağlantıyı sağlar. Her iki kaplamanın
sargıları
direkt
uçlara
bağlandırğından
MPkondansatörlerinde hemen hemen endüksiyon etkisi görülmez.
MP- kondansatörlerin özellikler kendi kendilerini onarma nitelikleri büyük bir yarar sağlar.
Bilinen alümunyum tabakalı kağıt-kondansatörlere değinle MP-kondansatörlerdeki metal kaplama
oldukça incedir. (0,01mm kadar) Herhangi bir şekilde bir kısa devre oluştuğunda bu kısa devrenin
ortaya çıktığı yerderki metal kaplama elektrik arkı nedeni ile buharlaşır.
Böylece ksıa devrenin oluştuğu yerin çevresindeki iletken metal uzaklaşarak devamlı bir bağlantı
hali önlenmiş olur. MP-kondansatörler , işletme güvenliğinin büyük ölçüde istendiği yerlerde,
özellikle kullanılmaktadır. Dış boyutlarının küçük olması nedeni ile büyük kapasite değerine (örneğin :
Her yapı ünitesi başına 50uF a kadar) ulaşılabilmektedir.
c) Sentetik tabakalı kondansatörler (simgesi = K )
Bu kondansatörlerde dielektrik olarak sentetik maddeden bir tabaka kullanılmıştır. Bu tabaka
üzerine ya alümünyum bir tabaka geçirilmiş ya da metalize edilmiştir (=metal buharına tutulmuştur).
Metalize sentetik tabakalı kondansatörler ek olarak M simgesini alırlar ve bunlar MPkondansatörler gibi kendi kendilerini onarabilirler. Dielektrik olarak amaç ve kullanmaya göre
aşağıdaki sentetik maddelerden yararlanılmaktadır.
Polikarbonat (Simgesi = C)
KC- kondansatörleri 220pF . – 1uF kapasite değerlerinde 50 V ... 630 V luk gerilimler için yapılırlar.
Politereftalat (Simgesi = T)
KT – kondansatörleri 1000pF ..... 0,33uF kapasite değerlerinde 100V .... 400Vluk gerilimler için
yapılırlar. MKT – kondansatörlerde üzeri metalize edilmiş bir politereftalasit esteri tabakası
dielektrik olarak kullanılır.
8
Bu tür kondansatörler 0,01uF .... 10uF kapasite değerlerinde 100V .... 630 V luk gerilimler
için yapılırlar.
Polistrol ( Styroflex) (Simgesi = S)
Özellikle kayıpsız ve kapasite kararlı olan KS- kondansatörleri 1pF .... 0,5Uf kapasite değerlerinde
30 V.... 500V luk gerilimler için yapılırlar.
d ) Seramik kondansatörler :
Bu kondansatörlerde dielektrik olarak seramikten bir madde kullanılır. Seramik maddenin
her iki yanı bir soy metalin buharına tutularak kaplanmıştır. Boru , tabla , şapka ve disk şeklinde
yapılan kondansatörlerin işletme gerilimleri 700V ‘a kadardır. İşletme gerilimi 12kV ‘a kadar
dayanıklı yüksek gerilim kondansatörleri çanak ve plaka şeklinde yapılırlar. Ayrıca 60kVA ‘lık anma
güçlerine kadar serkamik güç kondansatörleri bulunmaktadır.
e) Mika Kondansatörler :
Bu kondansatörler mikanın dielektrik olarak kullanıldığı tabakalı kondansatörlerdir. Mika
mineralinin çok küçük bir kayıp faktörü ve yüksek dielektrik dayanımı (40-60kV / mm) olup çok
büyük işletme sıcaklıklarında güvenlikle kullanılabilir. Mikalı kondansatörler özellikle yüksek frekans
ve ölçme tekniği için yalıtkandır.
f) Elektrolitik Kondansatörler :
Elko diye de tanınan bu kondansatörlerde kullanılan dielektrik, milimetrenin birkaç binde biri
kalınlığında yalıtkan bir oksit tabakasıdır. Bu kondansatörün pozitif elektrodu (anod) üzerine
elektrokimyasal bir yöntem ile alimünyum oksit kaplanmış bir alimünyum tabakasıdır. Diğer elektrod
(katot) ise elektrolitik bir maddedir. Elektrolitik madde ile taması bağlantı elektrodu sağlar.
Bağlantı elektrodu olarak bir metal kap kullanılır. Bu kap aynı zamanda anod ile elektrolit içine
alarak korur. Bazı elektrolitik kondansatörlerde plaka yüzeyini büyütmek amacıyla anod özel olarak
oluklu halde yapılmıştır. Kullanılan elektrolit sıvı , nemli ya da kuru ( örneğin nişasta gibi dolgu
maddeleriyle kıvamlandırılmıştır) olabilir.
Genellikle kuru elektrolitik kondansatörler kullanılır. Çinkü bunların montaj anında konum
şekli önemli değildir. Bunlarda elektrolit özel bir kağıda emdirilmiştir. Bu özel kağıt okside
alimünyum tabaka ile metalik alüminyum tabaksı arasına yerleştirilir ve hep birlikte sarılır. Çok ince
oksit tabakası nedeni ile bu değin bir sargının aynı büyüklükteki bir metal – kağıt sargısına nazaran
çok daha büyük bir kapasitesi vardır. Elektrolitik kondansatörlerin kutupları gerilime yanlış
bağlanırsa çok ince oksit tabakası indirgenerek bozulur. Bunun sonucu işletme gerilimi kısa devre
olur ve ortaya çıkan kısa devre akımı kondansatörü ısıtarak patlatır.
Elektrolitik kondansatörlere alternatif gerilim uygulanmaz.
Kutuplu – elektrolitik kondansatörlerin dışında alternatif gerilimde çalıştırabilecek
kutupsuz – elektrolitik kondansatörler vardır. Bunlar aynı kutupları birbirine seri bağlanmış iki adet
kutuplu elektrolirik kondansatör gibidir. Bu nedenler , örneğin anodaları bir araya bağlanmak ve
diğer uçları açıkta kalmak koşulunda iki adet kutuplu kondansatörden bir adet kutupsuz kondansatör
oluşturulabilir. Ancak bu kez , kapasite değeri yarıya iner.
Uzun süre kullanılmıyan elektrolitik kondansatörlerin kapasitesi kendi kendine azalır. Bu tür
kondansatörler kullanılmadan önce formasyon işlemine tutulur.Formasyon işleminde kondansatör
önce alçak gerilim altında uzan süre tutulmakta ve sonra yavaş yavaş gerilim arttırılarak anma
gerilimine ulaşılmaktadır.
Böylece kapasitenin azalmasına neden olan oksit tabakası bozuklukları onarılmaktadır.
Elektrolitik kondansatörler gerilime doğru bağlandıkları sürece oluşabilecek kısa devreleri kendi
kendilerine derhal onarabilirler.
9
Elektrolitik kondansatörler + %40 ile - % 20 toleranslar arasında ve 1000V’luk işletme
gerilimine kadar 4uF – 10000uF arası kapasitelerde yapılabilmektedir. Bu tür kondansatörlerin
kapasitesi çevre ısısına ve işletme süresine göre değişebilir. Elektrolitik kondansatörlerde devamlı
bir kaçak sızıntı akımı söz konusu olduğundan işletme anında ısınırlar.
g) Tantal kondansatörler :
Bu kondansatörler elektrolitik kondansatörlerin geliştirilmiş şeklidir. Tantal kondansatörler
de kutuplu kondansatörlerdir. Bunların kapasitesi sıcaklık ve gerilim değişmelerine karşı oldukça
duyarsızdır. Anod olarak ; tabaka , tel ya da sinterli levha şeklinde Tantal metali kullanılmıştır.
Katotda sülfirik asit ya da manganoksitten bir elektrolit bulunur. Kullanlılan dielektrik tantal
oksittir. Tantal kondansatörler modern elektronik teknolojisinin duyarlı aygıtlarında sık sık
kullanımaktadır.
2. Değişken kapasiteli kondansatörler.
a) Varyabl Kondansatör :
Bu kondansatörler genel olarak , birbirlerinden yalıtılmış plaka bloklarından oluşmuştur.
Bloklardan bir sabit olup kondansatör gövdesine izolatörlerle oturtulmuştur. Hareketli blok bir mil
üzerinden döndürülebilir olup gövdeye elektriksel bağlantılıdır. Milin döndürülmesiyle hareketli blok
plakalar , sabit plakalar arasına girip çıkarak kapasite değeri ayarlanabilir.
Aynı mil üzerine birkaç hareketli blok plaka ve bunların karşılarına sabit plakalar
yerleştirilmek suretiyle tek gövde üzerinde birkaç varyabl kondasatör elde edilebilir. Bu tür imal
edilmiş varyabl kondansatörler örneğin Ganglı varyabl kondansatör olarak tanınır. Genellikle varyabl
kondansatörlerde dielektrikolarak hava ve ender olarak mika ya da fiber kullanılmaktadır.
Bugün radyoların ve telsizlerin frekans ayarında büyük ölçüde
kullanılan varyabl
kondansatörlerin havalı tipleri gang başına azami 600pF lik bir kapasite gösterirler.
b) Trimer kondansatörler :
Bu kondansatörlerde biri hareketli , diğeri sabit olmak üzere iki seramik disk bulunur.
Diskler metal buharında yarım daire şeklinde , örneğin gümüş kaplanmıştır. Hareketli disk çevrilmek
suretiyle bu yarım daireler az ya da çok üstüste getirilerek kapasite ayarlanır. İnce ayarlar için
kullanılan trimer kondansatörlerin kapasiteleri 5pF .... 75pF arasındadır.
Osilatör ve dalga bobinlerinde yoğun ölçüde sabit ayarlar (Kalibrasyon) için kullanılan trimer
kondansatörler disk , şapkalı ve tüp şekillerinde boy boy imal edilmektedir.
4 . ALTERNATİF AKIM DEVRESİNDE KONDANSATÖR :
1) Kapasitif reaktans :
Bir doğru gerilim kaynağı bir Kutup çevirici üzerinden 4uF
lık
bir
kondansatöre
bağlanmıştır. Akım devresine seri olarak alternatif akım ölçen bir ampermetre bulunmaktadır. Bir
motorun kollektörüne benzeyen kutup çevirici döndürüldüğünde doğru gerilim, alternatif gerilime
dönüştürülür ve devreden alternatif akımın geçtiği görülür. Kutup çevirici daha hızlı döndürüldükçe
geçen akımın yükseldiği izlenir.
Kutup çeviricinin döndürülmesiyle , bunun çıkışında doğru gerilim devamlı polarite değiştirir
ve bunun sonucu kondansatöre bir alternatif gerilim uygulanmış olur. Bir kondansatöre alternatrif
gerilim uygulandığında, plakaları değişken bir şekilde pozitif ve negatif yüklenir. Bu farklı
yüklenmeler alternatif gerilimin iletken üzerindenki ritmi ile pozitif ve negatife doğru salınır. Bunun
sonucu iletkenlerden kondansatöre doğru bir alternatif akım akar. Gerçekte bir kondansatörde
alternatif akımın aktığı varsayılır. Bu nedenle buna bağıl akım ya da izafi akım denilir.
Alternatif akım devresindeki bir kondansatör geçen akıma bir direnç gibi karşı koyar.
Bu tür bir direnç kapasitif reaktans (Xc) olarak anılır. Kapasitif reaktansa bazı çevrelerde
kapasitans ya da kapasitif tepkin direnç de denilmektedir. (Reaktans = Reaktif Rezis tans =Tepkin
Direnç)
10
Frekans ne denli yüksek olursa , kapasitans o değin küçük olur .
Yukarıda anılan sınamada 4uF lik kondansatör yerine önce 8uF lik sonra 16Uf lık
kondansatörler konulduğunda devreden geçen akımın yükseldiği görülecektir.
Kapasite ne denli büyük olursa , kapasitans o değin küçük olur.
Xc = 1 / C
Xc = Kapasitans (æ) = Açısal frekans ( rad ) C = Kapasite (F)
Örnek : 50 Hz ‘ lık bir alternatif gerilimde 10uF lik bir kondansatörün kapasitansını hesaplayınız.
Çözüm : Xc = 1 / 2 f C = 100000 / 2 . 3,14 . 50 = 318,5
Kapasitans bir direnç gib düşünülürse Ohm yasası burada da uygulabilir.
Ic = U / Xc
Örnek : Kapasitansı 1600æ hesaplanmış bir kondansatöre 50Hz ve 220 V luk bir gerilim
uygulanmıştır. Devreden geçen akımı bulunuz.
Çözüm : Ic = U / Xc = 220 / 1600 = 0,137 A
2. Kondansatör Devreleri :
a) Paralel devre :
Bir çok kondansatörün paralel bağlanması plaka
yüzeyinin büyütülmesi gibidir. Bu nedenle C eşdeğer
kapasitesi paralel kapasitelerin tek tek toplamıdır.
Bir çok kondansatörün paralel bağlanmasında
eşdeğer kapasite tek tek kapasitelerinin toplamında
eşittir.
C = C1 + C2 + .......Cn
Örnek : 1000pF ; 0,02uF ve 5nF lık üç kondansatör paralel bağlanırsa eşdeğer kapasite ne olur?
Çözüm : C = C1 + C2 + C3 = 100 + 20000 + 5000 = 26000pF = 0,026uF
b) Seri Devre :
Bir çok kondansatörün seri bağlanmasında eşdeğer kapasitans seri kapasitanslarının
toplamına eşittir.
Xc = Xc1 + Xc2 + Xc3
+
....
Bir çok kondansatörün seri bağlanmasında eşdeğer kapasitenin ters değerliği tek tek
kapasite değerlerinin toplamına eşittir.
11
Seri bir devrede eşdeğer kapasite en küçük seri kapasiteden daha küçüktür.
Kondansatörlerin seri bağlanması plaka ara mesafelerinin büyütülmesi gibidir. Seri bir devrede
bulunan her kondansatörde toplam gerilim bölündüğü için , tüm seri devrenin gerilim dayanımı her
bir kondansatörün tek tek gerilim dayanımından büyüktür.
Yalnız iki kondansatörün seri bağlantısında, eşdeğer
kapasite :
Örnek : 10uF ve 2uF lik seri bağlanmış iki kondansatörün eşdeğer kapasitesini bulunuz.
Çözüm :
C = 10 . 2 / 10 + 2 = 20 / 12 = 1,66 uF
3 ) Kondansatörlerde faz kaynası :
Şekilde de gçrüldüğü gibi bir ölçme devresi kurulmuştur. Devrede seri olarak bir
ampermetre ve kondansatöre paralel bağlı bir voltmetre bulunmaktadır. Tüm devre akım devresine
bağlanmadan önce bütün ölçü aletleri sıfırı göstermektedir.
Bu devre 10 V’luk bir doğru
gerilim kaynağına ilk bağlanma anında
kondansatör plakaları arasında ölçülen
gerilim sıfırdır. Uygulanan gerilim ile
(şarj gerilimi ) kondansatör gerilim
arasında çok büyük bir fark olduğu için ,
şarjın başlangıcında kondansatöre doğru
büyük bir akım akar ve ampermetre en
büyük değeri gösterir. Şarj ilerledikçe
kondansatör gerilimi de artaya başlar.
Bunun
sonucu
şarj
gerilimi
ile
kondansatör gerilimi arasındaki fark
azalır ve kondansatöre doğru akan akım
düşmeye başlar. Kondansatör tam şarj edildiğinde kondansatör gerilimi ile sarj gerilimi birbirine
eşit olur ve şarj akımı sıfıra düşer. Alınan bu evreleri kolaylıkla izliyebilmek için devreye seri halde
bir direnç konulmuştur.
Buradan bir kondansatörde , ancak bir şarj akımı ile önceden şarj edilebildiği taktirde bir
gerilimin bulunabileceği anlaşılmaktadır.
Saf kapasitans gösteren bir alternatif akım devresinde akım 1 / 4 periyot kadar gerilimin
önündedir. Bu nedenle gerilim ile akım arasındaki faz farkı açısı 90 dir.
Kondansatörlerde akım gerilimin 90 önünden gider .
Şekilde görülen devre bir kutup çevirici
üzerinde bir doğru gerilim kaynağına (G) bağlıdır.
Kutup çevirici döndürüldüğünde , paralel devrede
önce kondansatör (C) ayağına bağlı lamba ; sonra
direnç (R) ayağına bağlı lamba yanacaktır. Buradan
bir alternatif akım devresinde bir kondansatörün
bir bobine göre aksi yönde bir fdaz farkı
oluşturduğu anlaşılır.
4 ) Kondansatörde kayıplar :
Kondansatörlerin hepsine işletme anında kayıplar ortaya çıkar. Bu nedenle kondansatörler saf
kapasitans gösterememektedir. Bu kayıpların bir kısmı , her yalıtkanın bir ölçüde iletken olmasından
doğar. Bir kondansatörde alternatif gerilim uygulundığında dielektrik içindeki moleküler dipoller
devamlı döner. Bu nedenle enerjinin bir kısmı ısı halinde yitirilir.
12
Bu özellikten yararlanarak yüksek frekanslarda yalıtkan maddelerin dielektriksel ısıtması
yapılır. Örneğin plastik maddelerin yapıştırılması, kerestelerin kurutulması ve kızartma fırınları gibi.
Sargılı kondansatörlerde bağlantı uçları tabakaların başlangıç kısımlarına bağlı olduğu için,
şarj akımı şerit şeklindeki sargılar boyunca akmak zorundadır. Bu nedenle bu metal tabakarın da
ohmik bir direnci vardır.
Bir kondansatörde anılan bütün bu kayıp türleri kayıp direnci (R) adı altında toplanabilir.
Bütün kayıplar ısı halinde ortaya çıktığından R kayıp direnci etkin bir dirennçtir. Bu etkin direnç bir
Iw kayıp akımını oluşturur. Bir kondansatörde bu değin bir etkin direnç kayıpsız kondansatöre
paralel bağlanmış bir direnç halinde düşünülür.
Kayıpları da göz önüne alarak kondansatörer birbirine paralel bağlı
kapasitans ve etkin dirençlerle gösterilir. Dielektrik içindeki kayıplardan
dolayı gerilim ile akım arasındaki faz açısı tam 90 olmayıp daim 90 den
küçüktür. 90- kadarlık bir fark kayıp açısı açısı olar anılır. İyi kaliteli
kondansatörlerde kayıp açısı bir derecenin 60 – 50 de biri kadardır.
Uygulamada genellikle kayıp açısının tanjantı kullanılır. Kayıp
açısının tanjantı kayıp faktörü
olarak anılır. Paralel bağlantılı bir
devrede kol akımları , üzerinden geçtikleri dirençler ile ters orantılıdır.
Kayıp faktörü frekansa bağlı olarak değişir. Ancak bazı hesap işlemlerinde kolaylık getirmesi
amacı ile, kondansatörler yalnızca kapasitans halinde kabul edilmekte ve kondansatör içindeki
kayıplar ihmal edilebilmektedir.
5 ) Kondansatörlerde güç :
Saf kapasitif bir yüklenmede alternatif akımın güç eğrisi <<u>> ve <<i>> ani değerlerinin
çarpımı sonucu elde edilir. Bu gücün ortalama değeri sıfırdır.
Kayıpsız kondansatörler yalnızca tepkin güç çekerler.
Tepkin güç kondansatör içinde elektrik alanının kurulmasına yarar. Elektrik alanı yol olduğu
zaman bu güç kaynağa geri gönderilir. Bir kondansatördeki enerji kondansatör ile gerilim kaynağı
arasında gidip gelerek salınır.
Bundan dolayı kondansatöre giden iletkenlerden tepkin akım geçer.
ETKİN VE TEPKİN DİRENÇLİ DEVRELER
Bir kondansatör ile bir dirençten oluşmuş bir
seri devreye gerilim uygulandığında R etkin direnci
üzerine bir Uw gerilimi ve X tepkin direnci üzerinde
bir Ubc gerillimi düşer .Güç faktörü kapasitif tepkin
dirence (kapasitans) ait sıfır değeri ile etkin dirence
ait değeri arasında bulunur.
Bulunan gerilimlerin ilgili akımlara bölünmesi
ile gerilim üçgeninden direnç üçgeni elde edilir.
13
Örnek : 10uF lik bir kondansatör 1000æ luk bir direç ile seri bağlanmıştır. Bu seri devreye 220 V /
50 Hz lık bir gerilim uygulanırsa empedansını bulunuz.
Çözüm :Eğer Xc bulunursa yukarıdaki formül ile Z yi bulabiliriz.
Etkin
bir
direnç
bir
bobine
seri
bağlandığında bu direncin bobinin etkin
direnci ile toplanması gerekir.
14