STATİK MAGNETİK ALAN

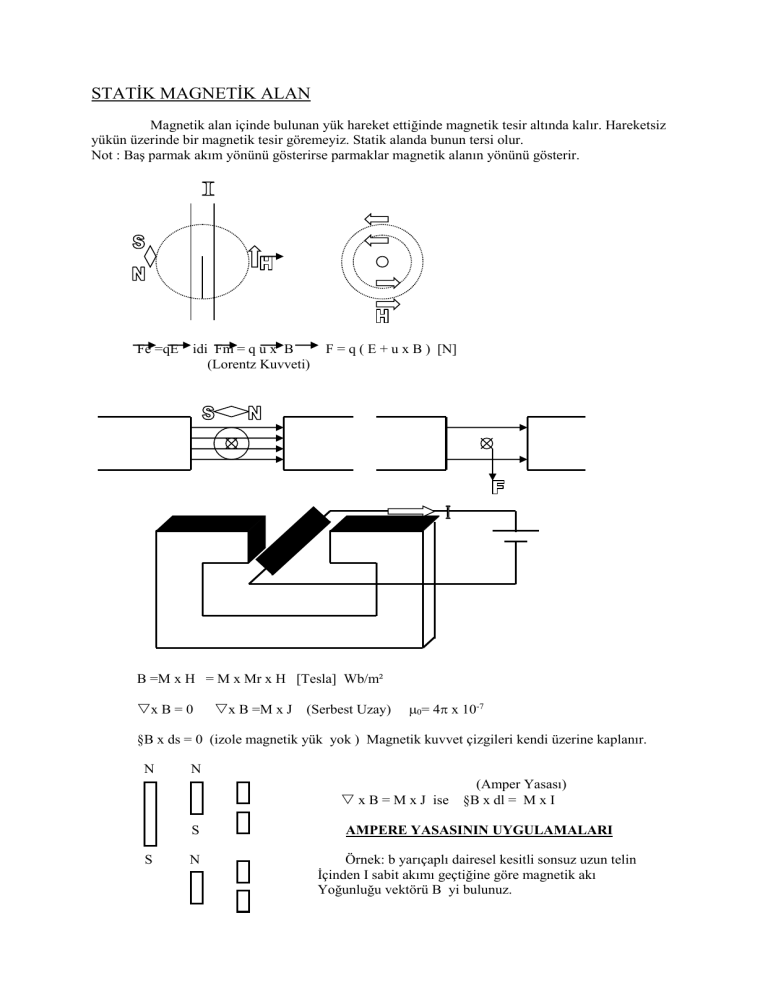
STATİK MAGNETİK ALAN
Magnetik alan içinde bulunan yük hareket ettiğinde magnetik tesir altında kalır. Hareketsiz
yükün üzerinde bir magnetik tesir göremeyiz. Statik alanda bunun tersi olur.
Not : Baş parmak akım yönünü gösterirse parmaklar magnetik alanın yönünü gösterir.
Fe =qE idi Fm = q u x B
(Lorentz Kuvveti)
F = q ( E + u x B ) [N]
B = x H =  x r x H [Tesla] Wb/m²
x B = 0
x B = x J (Serbest Uzay)
0= 4 x 10-7
§B x ds = 0 (izole magnetik yük yok ) Magnetik kuvvet çizgileri kendi üzerine kaplanır.
N
N
(Amper Yasası)
 x B =  x J ise §B x dl =  x I
S
S
AMPERE YASASININ UYGULAMALARI
N
Örnek: b yarıçaplı dairesel kesitli sonsuz uzun telin
İçinden I sabit akımı geçtiğine göre magnetik akı
Yoğunluğu vektörü B yi bulunuz.
a) İletken içinde r<b
B1 =aΦ x BΦ1 dl = aΦ x r1 x dΦ
§B1 x dl = §BΦ1 x r1 x dΦ
R2
B
c1
R1
C2
= 2r1 x B Φ1
c1 in içinden geçen akım I1= r1²/ b² I= ( r1/ b) ² x I o halde ampere yasasından
B1 = aΦ x B Φ1 = aΦ (( x r1 x I ) / 2b² ) r1<b
B
b) iletkenin dışında r>b
B2 = aΦ x B Φ2
dl = aΦ x r2 x dΦ
§B2 x dl = 2r2 x B Φ2
( x I) / 2
B2 = aΦ x B Φ2 = aΦ (( x I ) / 2r2 )
r2>b2
C2 nin içindeki toplam akım I kadar.
Örnek:Toroidal Bobin
a
b
r
c

r
Ferromanyetizma Olayı:
Herhangi bir demir bileşiği, Demir (Fe),Ni,Co vs gibi bazı metaller
nonlineer özellik gösterir.(Nonlineer, bellekli)
B
Başlangıç noktasına dönemez.Buna “artık
mıknatıslanma” denir.Sistemin bellekli ve nonlineer olmasından kaynaklanır.
H
Ferromanyetizmanın Fiziksel teme elektron spini
Elektron spini kendi ekseni etrafında dönüşe tekabül
eden bir akım gibi yorumlana bilir.Mikroskobik bir
manyetik alana sahip.
Histerizis Eğrisi
Alan kaldırılınca tekrar dağılırlar yalnız ferromanyetik malzemelerde alan kaldırılırsa bile şekilleri bozulmaz bir magnetik alan oluşur yani artık mıknatıslanma elektronların yöneliminden kaynaklanır.
Örnek: Sonsuz uzun bobinin oluşturduğu magnetik alan yağ vektörü 5’yi içinden geçen
akım I ve birim uzunluk başına sarım sayısı ne olması durumun içini bulunuz.
1
1
Bir alan
uygulanırsa
dizilirler
B.dl   o I

Biot Sowart
ç
 
Idl sin    I RxL

dB= k
dB 
ç | R |3
r2
B  k
IL sin 
r2
B.L   o nLI  B   o nI
k
Magnetik Vektör Potansiyeli


.B  0  B  xA




xB   o J  xxA  .(.A)   2 A   o J .A  0 seçilir



J
 2 A   o J  o  1 dv1
ç V1 R
2V 
g
1
g
1

dR
1


4  v1 R


B  0   Bd s s  0
 
B
 .ds  
 

x
A
 ds  
Magnetik Akı

 Adl  
[ Wb ]
c
Biot-Savort Yasası ve Uygulamaları
Jdv1=Jsde1=Ide1
  I dl1
A o 
4 c1 R

 M o I dl1 xa R
Wb / m B  xA' dan B 
[ I]
4 c R 2

  o I  dl1 xR 



 yada dB 
 R 3 [T]
4





Diferansiyel akım elemanı (Idl)’nin herhangi bir R pozisyonundaki magnetik akı yoğunluğu



vektörüne etki d B ile gösterilirse R pozisyonundaki magnetik alan B   dB ile hesaplanabilir.


  o I  dl1 xa R

B   dB [I] dB 
4  R 2
c1
p
B = F/(IL)= Kuvvet/(AkımMomenti)
+
dF= IBdLsin 
S
=
N
S
N
F
F = BIL
( Birim akım momenti başına düşen kuvvet )
L: İletkenin boyu
I : Telin içinden geçen akım
B: Manyetik alan
F = (IB)L
dF = (IB)L (Motor Denklemi)
Örnek : İçinden I akımı geçen 2L uzunluğundaki telin orta dikmesi üzerinde oluşan
manyetik akı youğunluğu vektörü B ‘yi
a)) Öncelikle manyetik vektör potansiyeli A ‘yı hesaplayarak
b)) Biot-Savart yasasını uygulayarak bulunuz.
dz
R
a) dl’ = dz’az
A =I/4 dl’/R [ Wb/m]
A = az I/4  dz’/(z’2+r2) = az I/4 [ In ( z’+(z’2 +r2)]
L
+L
-L
z
r
p(r,0,0)
L
A = az I/4 In (L2+r2) +L B= *A = *(azAz)
L2+r2 –L
B= ar1/r  Az/A-aAz/r
Silindirik simetriden dolayı telin etrafında Az/ = 0 olduğuna göre
B = -a /r [A]  B= IL
[T] r<<L  B=a I/2r [T]
2rL2+r2
b) Biot_Savart yasasından hareketle B’nin bulunması
dB=I/4(dl’*R/|R|) [T]
dl’ = azdz’ R= rar-zaz dl’*R = ardz’
dB = I/4 (dl’*R/|R|3) [ [T] dl’= azdz’ R = rar-z’az dl’*R = ardz’
dB = I/4 rdz’/|R|3 a
+L
+L
B=  dB = a/4  rdz’/(z’2+R2)3/2  B = IL a [T]
-L
-L
2rL2+r2
Ödev: İçinden I akımı geçen karesel çevrimin merkezindeki magnetik akı youğunluğu
vektörü B ‘ yi bulunuz .
z
Bir tane w genişliğinde içinden I akımı geçen telin etkisi
B = IL/2rL2+r2 az
W
I
L = r = w/2 ise
B = I/2 w olur.
Diğer 4 farklı içinden I akımı geçen telin etkidisi de aynı olacağından
B = I/2w*4 [T] olacaktır.
54
ikinci ve daha önemli bir özel durumda R >> a ve (1-u)ֿ³′² 1+3u , u<<1
2
2
H= I0
∫ [ aR Z.cos' + ayZsin'- aZ (ysin' + xcos'- a)]  1+3axcos' + 3aysin'd
4R³ '=0
 R²

sin² ve cos² ‘ nin integralinden ,sin' , cos' nin integralinden 0 gelecek.
H= Ia² aR 3xz + ay 3yz – az  3y² + 3x² - 2 
4R³  R²
R²
 R²
R²

Z/R=cos , x/R=sin.cos , y/R=sinsin
ve x²+y² /R² =  r  sin² yazılıp düzenlenirse
 R² 
[ ] = aR 2cos + asin
a²=S ise
H = I.S (aR 2cos + a sin ) = m (aR2cos + asin) [A/m] m=IS ,Mag. Dip. Moment
4R³
4R³
E = P ( aR 2cos + a sin) [V/m] p= o .d,
4€0R³
Elektr. Dip. Momen.
Magnetik Alanlar İçin Sınır Koşulları
.B =0
Magnetik alanın normal bileşeni süreklidir. B1n = B2n, 1H1n=2H2n
.D =s
a n2.(D1-D2) = s
.H = J §H.d=I
=H1.w + H2..(-w)=Jsn.w
H1
H1t – H2t =Jsn [A/m]

w

h
an2 x (H1 – H2) = Js [A/m]
>
H2
an1
Magnetik Enerji
Wm=1/2  B.H.dv = 1/2 H²dv
v
Self Endüktansı
L[H] L=Φ = s B.ds
I
§H.dl
Φ=L.I
Wm=1/2.LI²
Örnek : İçinden I 0 akımı geçen z
self indükktansını bulunuz.
z
r>a
a
ekseni boyunca uzanan a yarıçaplı silindirik telin
 H .de  I  H rd  I
T
0
 H 
I0
r>a
2r
I0  r 2
I0r
 H  rd   a 2  H   2  a 2 r<a
Telin içinde ( r<a ) depolanan enerji ( birim uzaklıkta )
2
a 2
2
1
1
1   2
 I r 
Wm    H d     c  0 2  rddr   c  I 0
2
2 r 0  0  2  a 
2  8 
Wm 

1
2
Lint I 0  Lint  0
2
8
Örnek :
Şekildeki iç içe D uzunlugundaki iki iletken silindir her iki
ucundan kısa devre edilmiştir..iki silindirin arası magnetik
 malzeme ile doldurulmuştur.Buna göre
geçirgenliği
dan
self indksiyonu bulunuz.
z
b
I0

a
 z 2  a
js  
I
 a 2 0

2b
a
js
js
D
 0
 I
H   0
2 r
 0
r b
I0

a
 r 2  r
Js  
I
 a r 0

2 r
ra
ar b
br
sabit
 düzlemden geçen manyetiik akı;
js
D

b
 
z 0 r 0
x
L
ra
I 0
2r
drdz 
DI 0
b
ln  
2  a 
y
sonuç bu yapıda depolanan enerjiden de bulunabilir.

D  b Aynı

L
ln  
I0
2  a 
D b
1
1 DI 0
 I 
b
Wm      0  rdrddz 
ln  
2 b 0 r 0  2  r 
2 2
a
2
Wm 
1
D  b 
2
LI 0  L 
ln  H 
2
2  a 
Seri Bağlama :
D

c
 
z a r a
2
1 I 0
2r
Paralel Bağlama :
Leş  L 1  L2
D
drdz 
b
 
z  a r c
 2I
0
2r
drdz 
1
1
1


Leş L1 L2
DI 0 
c
 b 
1 ln     2 ln  

2 
a
 c 
b
1
a
c
2
zD
z0
KARŞILIKLI ENDÜKTANS
I2
1  L11I1  L12 I 2
 2  L21I1  L22 I 2
I1
L2
indüktans
self
L1
L11, L22
L12, L21
karşıklık endüktas
L12  L21
Örnek : Öz eksen boyunca uzanan üzernden I 1 akımı geçen talin şekildeki dikdörtgen
çevrede oluşturduğu net akıyı ve karşılıklı endüktansı bulunuz.
z
d
w
H 
h d w
I1
2r
 21 
h
I1
 21 
L 21 
 
 0 I1
2r
z 0 r  d
drdz
 0 hI 1
 d  w
ln 

2  d 
0h 
w
ln 1  
2 
d
H 
Örnek : Birim uzunluk başına sarım sayısı N olan sonsuz uzun bbinin self endktansını
bulunuz.
 H.dl  Hl  lNI  H  NI
l
B  NI
   B.ds  B.S  NIS
B
Birim uzunlugun endüktansı
  N
L
Örnek :
L2 , N 2
i
L1 , N1
 N 2 SI

 L  N 2 S
I
I
2b
N 2 sarımlı bobinden I akımı geçtiğine göre karşılıklı endüktansı bulunuz.
12  L12 I
12  B.S2  
N2
.I
l2
B
N2
.I  b 2
l2
12  N112
L12 
12
NN
 L12   1 2  b 2
I
l2
57
MAGNETİK DEVRELER
Ferromagnetik malzemelerden oluşan içinden magnetik akı geçen devrelerdir.
 
   B d s    B S kullanılarak
n
1) Düğüm denklemi

i
i 1
0
Gelen Akılar Toplamı = Giden Akılar Toplamı
Akı akım gibi düşünülebilir.
Sarım sayısı
 
2) Çevre denklemi  H . de  I  H  i  I i . n i
i
Örnek
A
 
Jds

H

 . de
Za
NI = HI  I + Ha  a
I
R
N
a
a
=
B I  I Ba  a

M1
Ma
Magnet,l akının nominal bileşeni sürekli olduğuna
MI
göre
LI
B = BI = Ba = A
Bu durumda
 I
 
 a    Vm  1   2  
 1 A  a A 
NI = 
Vm = magnetomotor kuvveti (Gerilim kaynağı yerine)
 = Reluktans (Direnç yerine)
Akı (Akım yerine)
 B . ds  BA
Örnek : Aşağıdaki şekilde verilen elektromagnetik röle direnci 2.6  olan 138 sarımlı
bobinle 24 V’da uyarılıyor. Dökme çelikten yapılan 0,1 m2 kesitli iki bölümün reluktansları
sırasıyla R1 = 324 H-1 ve R2 = 122 H-1 olarak verildiğine göre
a) İki parça birbirine dokunduğunda (röle enerjilenince) oluşan magnetik devrenin akısını bul.
b) İkinci parça ana gövdeden 1 mm uzaklaştığında devrede dolaşacak magnetik akıyı hesapla
24 V
24 V
138 sarım
1 mm
I=
E ??? 24V

 9,321 A
R
2,6
Vm = N . I = 138 . 9,231 = 1273 . 88A
Soru: L1= 12cm S1= 8cm2 L2
L2= 15cm S2=5cm2
VM,hava= ? ; VM,çelik= ?
B1= 0,8 Wb/m2
N= 1500
S2
0,4cm
L
1
S1
 
Vm   H .dl
Vm N .I  H1 .L1  2H 2 .L2  H hava .Lhava
B1 S1  B2 S 2  Bhava .S 2
0,8.8  10 4  B2 5  10 4  Bhava 5  10 4
B2  1,28Wb m 2 Bhava  1,28Wb m 2
H hava 

1,28
 1019108 A m 2
7
4 10

Vm,hava  H hava .Lhava  4076,4 A.t
B1  0,8Wb m 2  H1  110 A m ; B2  1,28Wb m 2  H 2 475 A m
Vm  N .I  1500.I  H 1 L1  2 H 2 L2  H hava Lhava
 110.12  10  2  2.475.15.10  2  4076,4
 13,2  142,5  Vm ,hava  Vm ,çelik  155,7 A.t
1500.I  155,7  4076,4  4232,1  I  1,8214 A
Soru:
Φ1
Φ1
L1=10cm
S1=1cm2
Φ2= Φ1
L2=3cm
S2=2,4cm2
n=1200 I=9mA
nI  H 1 L1  H 2 L2
9
 H 1 L1  H 2 L2
1000
2 S
10,8  H 1 L1  1 1 .H 1 .L2
2 S2
1200.
B2 S 2  2 B1S1


2 1.10  4
10,8  H 1 10.10  2  1
.3.10  2 
4
 2 2,4.10


2
H 1  86,4 A m  B1  0,434 Wb m
 2 H 2 S 2  2 1H1S1
2
S
H 2  1 H1 1
2
S2
H 2  72 A m  B2  0362Wb m 2
Soru: Bir elektromagnetik röle 10 cm ortalama uzunluklu bir (kesiti 1 cm2) nüve ve 1mm
uzunluklu seri hava boşluklu (röle enerjilenmediğinde) bir yapıya sahiptir. Hava boşluğunun
kesitinde 1 cm2 kabul edilirse Elektomagnetik röle 5000 sarımlı içinden 15mA geçen bobinle
enerjilendiğine göre hareketli parçaya etkiyen kuvvet hava boşluğu ;
a) 1mm
b) 0,4mm
c) 0,1mm
........için bulunuz. ( μr=1500)
Cevap:
Φ = B1.S1 =B0.S1=B.S
N.I = H1.L1 + H0.L0

0,10.10 2
0,1.10 4 
 = 15000 . 15 . 10-5

4
4 

.
1500
.
1
.
10

.
1
.
10
0
 0

N.I = Φ ( R1 + R2 ) = 

F .dl 

75. 0
 941,3 mWb 2
m
0,1000666
B2
2
2
2
s.dl 
dl  F1 

 7054,5 Nt
0 2
0 S
 0 S 4 10 71.10 4

Soru: AE ve FB bölümlerine seri olarak iki bobin bağlanmış ve içlerinden 2A akım
geçirilmiştir. Her bir bobin 400 sarımlıktır. Her hava boşluğunun uzunluğu 2mm ve etkin
kesidi 14,4cm ‘dir. Buna göre boşluktan geçen akıyı kaçak olmaması durumu için hesaplayın.
C
.
A
E
G H
B
F
D
C
A
E
G
H
F
l0
2.10 2
R0 

 11058
 0 .S 0 4 10 7
B
D


Vm
Vm
1273,88


 2,86Wb
 toplam 1   2 324  122
 gap 
l gap
 0 . Agap

0,001
 7957,75H 1
7
4 ..10 .0,1
Vm
Vm
1273,88


 0,078Wb
toplam 1  2  2 gap 324  122  2.7957,75
36,7 kat fark var.Relüktansla direnç arasındaki ilişkinin gösterilmesi

kesiti A
 cu
Cu
l gap
+
V

Rcu
R gap
Rcu
V  ( Rcu  R gap ).
 gap
Rcu 
l cu
 cu . A
R gap 
l gap
 gap . A
A

Vm



+
l gap
0
 gap
l
Vm  N .  (    gap ).
 
l
  .A
 gap 
l gap
 0 .A
ÖRNEK:
Yüksek permeabiliteli demir nüveli iki bobin ve orta kolunda hava aralıklı magnetik devrenin bütün
kolları orta kol hariç A kesitli,orta kol ise  g kesitlidir.Eşdeğer devreyi çiziniz. 1 ,  2 ve  g için
çözünüz.
2
1
l2
3
Vm1
1
a
2
2
1
3
l3
l1
l3
l1
l
; 2  2
; 3 
1 . Ag
1 . A
1 . A
Vm1  (1  23   a ).1  ( a  23 ). 2
 Vm 2  (23   a )1  ( 2  23   a ). 2
1 
l3
1
2
Vm1   1 .1 ; Vm 2   2 . 2 ; 1 
2
1
Vm 2
( 2  2 3   a ) .Vm1  (2 3   a ).Vm 2
1 . 2  (2 3   a ).(1   2 )
 g  1   2
;
a 
la
 0 . Ag
2 
(23   a ).Vm1  (1  23   a ).Vm 2
1 . 2  (23   a ).(1   2 )
Statik Magnetik Alanlarda Sınır Koşulları
Bölüm
Cinsi
A kesit
( m2 )
Ort.Akı
Yoğ.
 Akı
(Wb)
1
2
Dök.Çelik
Dök.Demir
0,16
0,18
3
Dök.Sac
16  10 4
8  10 4
16  10 4
8  10 4
8  10 4
8  10 4
  .
  i .li 
0,28
B
H

0,5 T
1T
275
10000
44
1800
0,5 T
65
18,2
1862,2
 9,31 A
200
Problem : Şekildeki magnetik devre 3 parçadan yapılmıştır.Dökme çelikten geçen  ‘nin 0,5 Tesla
olması için 200 sarımlık s
argıdan ne kadar akım geçmelidir? (Seri magnetik devre)
16 cm
4 cm
4 cm
Ort. Akı Yoğ.
1
20 cm
  .
2
N=200
2 cm
3
4 cm
4 cm
Akı değişmez.  ve  ise ortalama Akı yolu ve kesitin değişme nedeni ile değişir.
Problem : Paralel bağlı manyetik devrede
1
2
+
3
-
  .  
1
1
1
1



 1  2  3
Toplam Akı :   
0 . b
. ln
2
a
L
2
. ln
b
a
Örnek : Sonsuz uzun bobinin self endüktansı N : birim uzunluktaki sayısı
 .dl  .l  l..    .
   .dS = .S  ...S
Birim uzunluktaki endüktans
  .

  ..
L  . 2 .S
Örnek :
Karşılıklı Endüktansı
  .
12  L12 .i
2b L2,N2
2a
12  .S 2 
. 2
l2
. .b 2
12  1.12
i
L1,N1
L12 
.1 . 2
l2
2
.
l2
. .b 2
1  L1 .i1  L12 .i2
Örnek :
2  L21.i1  L2 .i2
l1
1
1
2
. I
3
L12  L21
l2
2
Silikon
çekirdek
Önemli Noktalar
I noktası için düğüm denklemi
2  1  3
l
3
Manyetik Devre
 (Akı)
 i .li
Elektrik Devre
i
Ri . i
n2 . 2  
Vi
Çevre Denklemleri
 .dl  n.
n
n1 . 1    i .Li
i 1
n
n2 . 2    i .Li
i 1
Örnek : l1  l 2  25 cm , l3  5 cm , S=1,3 cm 2 , 1   2  50 , 1  90  Wb ,
 2  120 Wb olması için 1 ,  2 ne olmalıdır? (Silikonlu çelik)(tablodan)
1  90  1 .S  1 .(1,3  10 4 )  1  0,69 Tesla , 1  8,7
ferro man.malzemelerde  sabit değildir ve çok yüksek man. alan depolayabilir.
 2 120  10 6
2 

 0,23 T
S
1,3  10 4
1 .1  1 .l1   3 .l3 (1)
 3  30  Wb
3 
 2  50 A/m
 2 . 2   2 .l 2   3 .l3 (2)
3
 0,92 
S3
 3  140 A/m
Şimdi bunları (1) ve (2) nolu denklemlerde yerine koyarsak
1  0,39
 2  0,75
 3  30 mWb