ANKARA ÜNVERSTES FEN BLMLER ENSTTÜSÜ YÜKSEK LSANS

ANKARA ÜNİVERSİTESİ
FEN BİLİMLERİ ENSTİTÜSÜ
YÜKSEK LİSANS TEZİ
ŞEKİL OPERATÖRÜ VE TEMEL FORMLAR
Merve BAYSAL
MATEMATİK ANABİLİM DALI
ANKARA
2007
Her hakkı saklıdır
Doç. Dr. Mustafa Kemal SAĞEL danışmanlığında, Merve BAYSAL tarafından hazırlanan bu
çalışma 14/02/2007 tarihinde
aşağıdaki jüri tarafından oybirliği ile Matematik Anabilim
Dalı’nda Yüksek Lisans Tezi olarak kabul edilmiştir.
Başkan : Doç. Dr. Mustafa Kemal SAĞEL
Ankara Üniversitesi Fen Fakültesi
Üye
: Yard. Doç. Dr. Nejat EKMEKÇİ
Ankara Üniversitesi Fen Fakültesi
Üye
: Prof. Dr. Baki KARLIĞA
Gazi Üniversitesi Fen-Edebiyat Fakültesi
Yukarıdaki sonucu onaylarım
Prof. Dr. Ülkü MEHMETOĞLU
Enstitü Müdürü
ÖZET
Yüksek Lisans Tezi
ŞEKİL OPERATÖRÜ VE TEMEL FORMLAR
Merve BAYSAL
Ankara Üniversitesi
Fen Bilimleri Enstitüsü
Matematik Anabilim Dalı
Danışman: Doç. Dr. Mustafa Kemal SAĞEL
Bu çalışma üç bölümden oluşmaktadır. Birinci bölümde temel tanım ve kavramlar ele
alınmıştır.
İkinci bölümde Weingarten dönüşümünün matrisinin hesabı ve temel formlarla ilgili
öklid uzayında hiperdüzlem, hiperküre, hipersilindir ve dönel yüzeyler için yapılan
çalışmalar ele alınmıştır.
Üçüncü bölümde ise Lorentz uzayında dönel yüzeyin Weingarten dönüşümünün
matrisinin hesabı ve ortalama eğriliğin temel formlar ile arasındaki ilişkiye ait
çalışmalar verilmiştir.
2007, 47 sayfa
Anahtar Kelimeler: Weingarten dönüşümü, Gauss eğriliği, Ortalama eğrilik ve temel
formlar.
i
ABSTRACT
Master Thesis
SHAPE OPERATOR AND FUNDAMENTAL FORMS
Merve BAYSAL
Ankara University
Graduate School of Natural and Applied Sciences
Department of Mathematics
Supervisor: Assoc. Prof. Dr. Mustafa Kemal SAĞEL
This study has occured three chapters. Basic description and concepts was evaulated in
first chapter.
In second chapter, it was evaluated in calculation of Weingarten map’s matrix and
relation to fundamental forms in euclid space, studies for hyperplane, hypersphere,
hypercylinder and surface of revolution.
In third chapter, it was mentioned that calculation of surface of revolution of
Weingarten map’s matrix in Lorentz space and studies which are relation to mean
curvature with fundamental forms.
2007, 47 pages
Key Words: Weingarten map, Gauss curvature, Mean curvature and fundamental
forms.
ii
TEŞEKKÜR
Bu çalışmanın yapılması fikrinden gerçekleşmesine kadar görüş, düşünce, bilgi ve
deneyimlerinden yararlandığım danışman hocam Doç. Dr. Mustafa Kemal SAĞEL’e ve
Ankara
Üniversitesi
Fen
Fakültesi
Dekan
Yardımcısı
Prof.
Dr.
Ender
YURDAKULOL’a teşekkürlerimi sunmayı bir borç bilirim.
Bu çalışmada bana her açıdan yardımcı olan hocalarım Prof. Dr. Yusuf YAYLI ve Yrd.
Doç. Dr. Nejat EKMEKÇİ’ye, Ankara Üniversitesi Çankırı Orman Fakültesinde görev
yapan Araş. Gör. Melda (BAYSAL) DÖLARSLAN’a, Araş. Gör. Emre Şahin
DÖLARSLAN’a ayrıca çalışmamın her aşamasında ilgi ve desteğini gördüğüm değerli
arkadaşlarım Seçil BATIR, Sevil BATIR, Engin KANIŞ’a ve her zaman maddi manevi
desteğini eksik etmeyen aileme teşekkürlerimi sunarım.
Merve BAYSAL
Ankara, Şubat 2007.
iii
İÇİNDEKİLER
ÖZET ........................................................................................................................................... İ
ABSTRACT .............................................................................................................................. İİ
TEŞEKKÜR ............................................................................................................................İİİ
SİMGELER DİZİNİ .............................................................................................................. Vİ
1. GİRİŞ ...................................................................................................................................... 1
2. TEMEL TANIM VE KAVRAMLAR ............................................................................. 2
3. ŞEKİL OPERATÖRÜ (WEINGARTEN DÖNÜŞÜMÜ) VE TEMEL
FORMLARLA İLGİLİ ÖKLİD UZAYINDA YAPILAN ÇALIŞMALAR ........ 9
3.1 Şekil Operatörü ve Temel Formlarla İlgili Teoremler ........................................ 9
3.2 E3 te Herhangi Bir Yüzey için Weingarten Dönüşümünün Matrisinin Hesabı 13
3.3 Gauss Dönüşümü ve Gauss Eğriliği ile Şekil Operatörü Arasındaki İlişki ...... 28
3.4 En de Bazı Özel Yüzeyler İçin Şekil Operatörü, Temel Formlar, K ve H
Fonksiyonları....................................................................................................... 29
3.4.1 Hiperdüzlemler için şekil operatörü, temel formlar, K ve H fonksiyonları... 29
3.4.2 Hiperküre için şekil operatörü, temel formlar, K ve H fonksiyonları............ 30
3.4.3 Hipersilindir için şekil operatörü, temel formlar, K ve H fonksiyonları ....... 33
3.4.4 Dönel yüzeyler için şekil operatörü, K ve H fonksiyonları ............................. 38
4. ŞEKİL OPERATÖRÜ (WEINGARTEN DÖNÜŞÜMÜ) VE TEMEL
FORMLARLA İLGİLİ LORENTZ UZAYINDA YAPILAN ÇALIŞMALAR 40
4.1 Lorentz Uzayında Dönel Yüzeyin Weingarten Dönüşümünün Matrisinin
Hesabı ile Gauss ve Ortalama Eğriliklerinin Hesaplanması ............................. 40
4.2 Lorentz Uzayında Temel Formlar ile Dönel Yüzeyin Ortalama Eğriliği
Arasındaki Bağıntı .............................................................................................. 43
iv
KAYNAKLAR ........................................................................................................................ 46
ÖZGEÇMİŞ............................................................................................................................. 47
v
SİMGELER DİZİNİ
Grek Alfabesi
A
α
Alfa
B
β
Beta
Γ
γ
Gamma
∆
δ
Delta
E
ε
Epsilon
Z
ζ
Zeta
H
η
Eta
Θ
θ
Teta
Ι
ι
İyota
K
κ
Kapa
Λ
λ
Lamda
M
µ
Mü
N
ν
Nü
Ξ
ξ
Ksi
O
o
Omikron
Π
π
Pi
P
ρ
Ro
Σ
σ
Sigma
T
τ
To
r
υ
Upsilon
Φ
ϕ
Fi
Χ
χ
Şi
Ψ
ψ
Psi
Ω
ω
Omega
vi
1. GİRİŞ
Bu çalışma çerçevesinde, öncelikle şekil operatörü ve temel formlar ile ilgili tanım ve
kavramlar ifade edilecek daha sonra, E3 te herhangi bir yüzey için Weingarten
dönüşümünün
matrisinin
hesabı
verilecektir.
Ayrıca,
hiperdüzlem,
hiperküre,
hipersilindir ve dönel yüzeyler için Şekil operatörü, Temel formlar, Gauss ve Ortalama
eğrilik fonksiyonlarını konu alan çalışmalara değinilecektir. Bununla beraber Lorentz
uzayında dönel yüzeylerin Weingarten dönüşümünün matrisinin hesabı ile Gauss ve
Ortalama eğriliklerin hesaplanmasının yanında, dönel yüzeylerin temel formları ile
ortalama eğrilikleri arasındaki bağıntıya yer verilecektir.
1
2. TEMEL TANIM VE KAVRAMLAR
r
Tanım 2.1: F : E n 
→ E m bir dönüşüm olsun. Eğer v P ∈ TE n (P) ise
r r
r
(F* ) P ( v P ) ∈ TE m (F(P)) de E m nin t 
→ F( P + tv ) eğrisinin t=0 daki hız vektörü
olsun. Böylece tanımlı
(F* ) P : TE n (P) 
→ TE m (F(P))
fonksiyonuna, F nin P∈ E n noktasındaki türev dönüşümü denir (Hacısalihoğlu 1994).
Tanım 2.2: F : E n 
→ E m dönüşümünün türev dönüşümü P ∈ E n için (F* ) P olsun.
Sırasıyla TE n (P) ve TE m (F(P)) de
Φ=
{
∂
∂x1
P
,...,
∂
∂xn
P
}
, Ψ=
{
∂
∂y1
F (P)
,...,
∂
∂y m
F (P)
} standart bazları
için (F∗)P nin karşılık geldiği matris F nin P noktasındaki Jakobien matrisi olarak
adlandırılır ve J(F,P) ile gösterilir.
 ∂ f1
 ∂x
 1
 ∂f 2
J(F,P) =  ∂ x1
 M
 ∂f
 m
 ∂ x1
P
P
P
∂ f1
∂x2
∂f 2
∂x2
M
∂f m
∂x2
P
L
P
L
O
P
L
∂ f1
∂xn
∂f 2
∂xn
M
∂f m
∂xn




P
 dir (Hacısalihoğlu 1994).


P

P
Tanım 2.3: M ve N birer C ∞ manifold ve
f:M
→ N bir C∞ fonksiyon olsun. Eğer f nin f * jakobien matrisi ∀ P ∈ M noktasında
regüler ise f ye M den N ye bir immersiyon denir (Hicks 1974).
Başka bir deyişle rank f = boy M ise f bir immersiyondur (Hacısalihoğlu 1994).
2
Tanım 2.4: N bir C∞ (n-1) manifold olsun.
f : N
→ E n fonksiyonu bir immersiyon ise f(N)=M manifolduna E n in bir
hiperyüzeyi denir (Hacısalihoğlu 1994).
Tanım 2.5: M bir diferensiyellenebilir manifold olsun. M üzerinde bir vektör alanı diye
X : M birebir
 −örten

→
U
TM (P)
P∈M
olarak tanımlanan X fonksiyonuna denir ve M üzerinde vektör alanlarının uzayı χ (M)
ile gösterilir (Hacısalihoğlu 1994).
Tanım 2.6: E n in bir hiperyüzeyi M, χ (M) de M yüzeyi üzerinde vektör alanlarının
uzayı olsun. χ (M) , χ ( E n ) in bir alt uzayıdır. χ ( E n ) deki iç çarpım işlemine göre
χ (M) in ortogonal komplemanı χ (M)⊥ olsun. χ (M)⊥ in bir ortonormal bazı {N} ise N
ye M nin birim normal vektör alanı denir (Hacısalihoğlu 1994).
Tanım 2.7: M bir C ∞ manifold olsun. M üstünde vektör alanlarının cümlesi χ (M) ve
reel değerli C ∞ fonksiyonların halkası da C ∞ (M , IR) olmak üzere,
,
: χ (M) x χ (M) 
→ C ∞ (M , IR)
fonksiyonu,
1) 2-lineer
2) Simetrik
3) ∀ X ∈ χ (M) için X , Y =0 ⇒ Y=0 ∈ χ (M)
özelliklerini sağlıyor ise, M ye yarı-Riemann manifoldu denir (Hacısalihoğlu 1994).
Tanım 2.8: M bir C ∞ manifold olsun. M üstünde vektör alanlarının uzayı χ (M) olmak
üzere,
D : χ (M) x χ (M) 
→ χ (M)
(X,Y) 
→ D(X,Y) = D X Y
fonksiyonu için
3
1) D fX+ gY Z = fD X Z +gD Y Z ,
∀ X, Y, Z ∈ χ (M) , ∀ f, g ∈ C ∞ (M,IR)
2) D X (fY) = fD X Y + ( Xf )Y ,
∀ X, Y ∈ χ (M) ,
∀ f ∈ C ∞ (M,IR)
özellikleri sağlanıyor ise D ye M manifoldu üzerinde bir afin konneksiyon denir
(Hacısalihoğlu 1994).
Tanım 2.9: M bir yarı-Riemann manifoldu olsun. D, M üstünde afin konneksiyon
olmak üzere
D : χ (M) x χ (M) 
→ χ (M)
[
,
,
]:
χ (M) x χ (M) 
→ χ (M)
: χ (M) x χ (M) 
→ C ∞ (M,IR)
fonksiyonları için,
i)
D, C ∞ sınıfındandır.
ii)
M nin bir A bölgesi üzerinde, C ∞ olan ∀ X, Y ∈ χ (M) için
DXY – DYX = [ X , Y ] dir.
iii)
M nin bir A bölgesi üzerinde, C ∞ olan ∀ X, Y, Z ∈ χ (M) ve ∀ P ∈ A için
X P Y , Z = D X Y, Z
P
+ Y, D X Z
P
dir.
Özellikleri sağlanıyor ise D konneksiyonuna M üzerinde bir Riemann konneksiyonu
denir (Hacısalihoğlu 1994).
Tanım 2.10: En in bir hiperyüzeyi M ve M nin birim normal vektör alanı N olsun. En de
Riemann konneksiyonu D olmak üzere ∀ X ∈ χ (M) için
S(X) = D X N ,
4
şeklinde tanımlı S dönüşümüne M üzerinde şekil operatörü veya M nin Weingarten
dönüşümü denir (Hicks 1974).
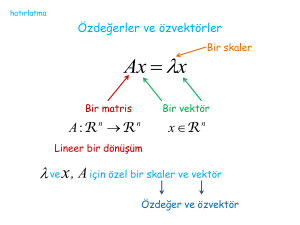
Tanım 2.11: A : V 
→ V lineer dönüşümü için
A( α ) = λ α ,
α ∈ V, λ ∈ R
r
olacak şekilde bir α ≠ 0 vektörü varsa λ reel sayısına A nın bir karakteristik değeri ve
α vektörüne de A nın bu λ karakteristik değerine karşılık gelen karakteristik vektörü
denir (Hacısalihoğlu 1982).
Tanım 2.12: Bir A: V 
→ V lineer dönüşümüne bir A ∈R nn matrisi karşılık gelir. Bu
A matrisi üzerinde tanımlanan
PA ( λ ) = det (A- λ In) = λn + a 1λn −1 + ... + a n −1λ + a n
polinomuna A’nın karakteristik polinomu, PA ( λ ) = 0 şeklindeki denkleme de
karakteristik denklemi denir (Hacısalihoğlu 1982).
Tanım 2.13: E n de bir hiperyüzey M ve M nin şekil operatörü S olsun. M nin bir P
noktasına karşılık gelen S(P) nin karakteristik değerleri M nin bu noktadaki asli
eğrilikleri olarak adlandırılır. Asli eğriliklere karşılık gelen ve karakteristik vektör
denen vektörlerin belirttiği doğrultulara da M nin P noktasındaki asli eğrilik
doğrultuları denir (Hacısalihoğlu 1994).
Tanım 2.14: E n de bir hiperyüzey M olsun. M nin bir P noktasındaki şekil operatörü
S(P) olmak üzere
K:M
→ IR
P
→ K(P) = det S(P)
biçiminde tanımlanan fonksiyona M nin Gauss eğrilik fonksiyonu ve K(P) değerine de
M nin P noktasındaki Gauss eğriliği (total eğrilik) denir (Hicks 1974).
Tanım 2.15: En de bir hiperyüzey M olsun. M nin bir P noktasındaki şekil operatörü
S(P) olmak üzere
5
H:M
→ IR
P
→ H(P) = İz(S(P))
biçiminde tanımlanan fonksiyona M nin ortalama eğrilik fonksiyonu ve H(P) değerine
de M nin P noktasındaki ortalama eğriliği denir (Hicks 1974).
Tanım 2.16: En de bir hiperyüzey M ve M üzerinde bir eğri α olsun. α nın teğet vektör
alanı T ve M nin şekil operatörü S olsun. Eğer T vektör alanı α eğrisi boyunca S nin
karakteristik vektörlerine karşılık geliyorsa α eğrisine M üzerinde bir eğrilik çizgisidir
denir.
Buna göre M üzerindeki eğrilik çizgilerinin diferensiyel denklemi
λ ≠ 0 bir skalar
olmak üzere S(T)= λ T şeklindedir (Hacısalihoğlu 1994).
Tanım 2.17: En in bir hiperyüzeyi M olsun. M üzerinde şekil operatörü S olmak üzere,
M hiperyüzeyi üzerinde q-uncu temel form diye, 1 ≤ q ≤ n olmak üzere,
Iq : χ (M) x χ (M) 
→ C ∞ (M,IR)
(X,Y) 
→ Iq(X,Y)= S q −1 ( X ), Y
şeklinde tanımlı Iq fonksiyonuna denir (Hicks 1974).
Buna göre,
I. Temel Form :
I : χ (M) x χ (M) 
→ C∞ (M,IR)
(X,Y) 
→ I(X,Y)= X, Y
,
II. Temel Form :
II : χ (M) x χ (M) 
→ C∞ (M,IR)
6
(X,Y) 
→ II(X,Y)= S(X), Y
,
III. Temel Form :
III : χ (M) x χ (M) 
→ C∞ (M,IR)
(X,Y) 
→ III(X,Y)= S 2 (X ), Y
şeklindedir.
Burada S2(X) = S(S(X)), S2=SoS dir.
Tanım 2.18: X= ( x 1 , x 2 , ... , x n ) ve Y= (y1 , y 2 , ... , y n ) ∈ IR n olmak üzere Lorentz
uzayında iç çarpım aşağıdaki şekilde tanımlanır:
<,>
L
: IR n x IR n 
→ IR
n −1
(X , Y) 
→ < X , Y >
L
= ∑ x i yi − x n y n
i =1
IR n üzerinde tanımlanan bu simetrik, bilineer ve nondejenere metrik tensöre Lorentz
metriği denir (O’Neill 1983).
Tanım 2.19: < , >
L
{
, IR n de Lorentz metriği olsun. IR n , < , >
L
} ikilisine n boyutlu
Lorentz uzayı denir ve L n ile gösterilir (O’Neill 1983).
Tanım 2.20: X = (x 1 , x 2 ,..., x n ) ∈ Ln ve X’ in normu X
L
= < X , X > olsun.
<X,X>
L
< 0
ise
X’e
time like vektör ;
<X,X>
L
= 0
ise
X’e
null vektör ;
<X,X>
L
> 0
ise
X’e
space like vektör denir ( O’Neill 1983).
7
Tanım 2.21: L n , n boyutlu Lorentz uzayı ve X , Y ∈ L n olsun.
<X,Y>
L
= 0 ise X ve Y vektörleri L n de birbirine ortogonaldir denir ( O’Neill
1983).
Tanım 2.22: X , Y ∈ L3 için vektörel çarpım şu şekilde tanımlanır:
∗ : L3 x L3 
→ L3
e1
e2
− e3
(X , Y) 
→ X ∗ Y = x 1
x2
x 3 (Tsagas and Papantoniov 1988).
y1
y2
y3
Tanım 2.23: ( r , z ) düzleminde bir eğri r = r ( t ) > 0 , z = z ( t ) ile verilsin.Eğer bu
eğri z-ekseni etrafında döndürülürse elde edilen şekle dönel yüzey adı verilir (Richard et
al 1977).
8
3. ŞEKİL OPERATÖRÜ (WEINGARTEN DÖNÜŞÜMÜ) VE TEMEL
FORMLARLA İLGİLİ ÖKLİD UZAYINDA YAPILAN ÇALIŞMALAR
3.1 Şekil Operatörü ve Temel Formlarla İlgili Teoremler
Teorem 3.1.1: En in bir hiperyüzeyi M ve M nin şekil operatörü S olsun.
1) S : χ (M) 
→ χ (M) dir.
2) S lineerdir.
3) S simetriktir.
İspat : 1) M nin birim normal vektör alanı N ise,
N, N =1 dir.
Buna göre X ∈ χ (M) için,
X [ N, N
] = X [1] ,
X [ N, N
] =0,
DX N , N + N , D X N = 0 ,
S ( X ), N + N , S ( X ) = 0 ,
2 S ( X ), N = 0 ,
S ( X ), N = 0 ,
S(X) ∈ χ (M)
bulunur.
Böylece ,
S : χ (M) 
→ χ (M) dir.
9
2) ∀ X, Y ∈ χ (M), ∀ a, b ∈ IR için,
S(aX+bY)=DaX+bYN
S(aX+bY)=aDXN+bDYN
S(aX+bY)=aS(X)+bS(Y) dir.
Bu da S in lineer olduğunu gösterir.
3) S nin simetrik olduğunu göstermek yerine S matrisinin self-adjoint olduğunu
göstermek yeterlidir.
(V, iç çarpım uzayı olmak üzere,
A:V 
→ V
lineer dönüşümü,
∀ x, y ∈ V için,
A(x), y = x, A(y)
önermesini doğrularsa A dönüşümüne simetrik (self-adjoint) dönüşüm denir. )
Buna göre,
∀ X, Y ∈ χ (M) için,
S(X), Y = X, S(Y)
olduğunu gösterelim.
X, Y ∈ χ (M) olduğundan,
X, N + Y, N =0
yazılabilir.
Buradan
10
X, N = 0 ve Y, N = 0 dır. E n de D operatörü Riemann konneksiyonu
olduğundan
Y [ X, N
veya
ve
veya
] =0
D Y X, N + X, D Y N = 0
…(1)
X [ Y, N ] = 0
D X Y, N + Y, D X N = 0
…(2)
yazılabilir. (2) den (1) çıkartılırsa
Y, D X N − X, D Y N + D X Y, N − D Y X, N = 0
elde edilir.
DXN = S(X), DYN = S(Y) olduğundan
Y, S(X ) − X, S(Y) + D X Y − D Y X, N = 0
D bir Riemann konneksiyonu olduğundan
D X Y - D Y X = [X, Y ] ∈ χ (M) dır. O halde
[X, Y], N
= 0 bulunur. Buradan
Y, S(X ) − X, S(Y) = 0 yani
Y, S(X ) = X, S(Y) elde edilir.
İç çarpımın simetri özelliğinden
11
S(X ), Y = X, S(Y)
olur. Bu da S in self-adjoint, dolayısıyla da simetrik
olduğunu gösterir (Hacısalihoğlu 1994).
Sonuç 3.1.1: S dönüşümünün matrisi simetriktir (Hacısalihoğlu 1994).
Teorem 3.1.2: (Cayley-Hamilton teoremi) Her matris kendi karakteristik polinomunun
bir sıfır yeridir (Hacısalihoğlu 1982).
Teorem 3.1.3: E3 ün bir hiperyüzeyi M olsun. M üzerinde I. , II. ve III. temel formlar
sırasıyla I, II, III ve gauss eğrilik fonksiyonu K, ortalama eğrilik fonksiyonu H olmak
üzere,
III – H.II + K.I = 0 dır (Kühnel 2006).
İspat: n=3 için boyM = 2 olduğundan, boyTM(P)=2 dir. O halde,
S : TM (P) 
→ TM (P) şekil operatörünün karakteristik polinomunun derecesi
ikidir. Üstelik S nin karakteristik değerleri olan k1 ve k2 asli eğrilikleri bu polinomun
birer sıfırı olduklarından, S nin karakteristik polinomu
PS( λ )= λ 2 – (k1 + k2) λ + (k1.k2)
şeklindedir. Cayley-Hamilton teoremine göre, S bu polinomun sıfırıdır. Böylece,
S2 - (k1 + k2)S + (k1.k2)I2=0 yazabiliriz.
Diğer taraftan ∀ XP ∈ TM(P) için,
[S2 - (k1 + k2)S + (k1.k2)I2](XP) = 0 ⇒
S 2 (XP) - (k 1 + k 2 ) S(XP) + (k 1 .k 2 ) XP= 0
ve ∀ YP ∈ TM(P) için,
S 2 (X P ) − (k 1 + k 2 )S(X P ) + (k 1 .k 2 )X P , YP = 0 ⇒
12
S 2 (X P ), Yp − (k 1 + k 2 ) S(X P ), YP + (k 1 .k 2 ) X P , YP = 0 yazılabilir. Buradan da
III(XP,YP) – (k1 + k2)II(XP,YP) + (k1.k2)I(XP,YP) = 0 bulunur. Bu da
III - (k 1 + k 2 ) II + (k 1 .k 2 ) I= 0 demektir.
K(P) = k 1 .k 2 ,
H(P) = k1 + k2 değerleri yerlerine yazılırsa ,
III – H.II + K.I = 0 elde edilir.
3.2 E3 te Herhangi Bir Yüzey için Weingarten Dönüşümünün Matrisinin Hesabı
E3 te bir yüzey M olsun. M nin parametrik ifadesi
Φ (u,v) = ( ϕ 1(u,v), ϕ 2(u,v), ϕ 3(u,v))
olsun. χ (M) nin bir bazı {V1 , V2} ise
S : χ (M) 
→ χ (M)
V1 
→ S(V1) = aV1 + bV2
V2 
→ S(V2) = cV1 + dV2
Burada karşımıza iki durum çıkar:
Φ (u,v) fonksiyonunun u ya göre türevi Φ u , v ye göre türevi Φ v olmak üzere;
I. Hal: Φ u , Φ v = 0 ve eğrilik çizgilerinin yüzeyin parametre eğrileri olması hali,
II. Hal: Φ u , Φ v ≠ 0 veya
Φ u , Φ v = 0 ama eğrilik çizgilerinin yüzeyin parametre
eğrileri olmaması halidir. II. hali çeşitli yöntemlerle I. hale çevirebiliriz.O halde I. hali
gözönüne alalım.
13
I. Hal:
Φu ,Φv = 0
olduğundan {Φ u , Φ v } sistemi χ (M ) için bir ortogonal bazdır.
Normlarsak
V1 =
1
Φu
Φu
V2 =
1
Φu
Φv
{V1,V2 } sistemi χ(M )
için bir ortonormal baz olur. M yüzeyinin birim normal vektör
alanı,
N = V1 Λ V2 =
1
Φu Φv
Φu Λ Φv .
O halde ,
S (V1) = D V1 N ,
S (V1) = D
1
Φu
Φu
N ,
S (V1) =
1
DΦu N ,
Φu
S(V1) =
1 dN
Φ u du
Şimdi
......................................................................... (3.1)
dN
yu hesaplayalım :
du
14
Φ uu , Φ u
Φ uv , Φ v
Φ ∧ Φ v + Φ u ∧ Φ uv
dN
− Φu ∧ Φv
− Φu ∧ Φv
= uu
3
3
du
Φu Φv
Φu Φv
Φu Φv
...... (3.2)
Şimdi , Φ uu , Φ uv , Φ vv yi hesaplayalım:
Φ uu = λ 1 Φ u + λ 2 Φ v + λ 3 N .
......................................................................... (3.3)
Burada λ1 , λ 2 ve λ 3 değerlerini bulalım.
Φ uu , Φ u = λ1 Φ u
λ1 =
Φ uu , Φ u
Φu
......................................................................... (3.4)
2
Φ uu , Φ v = λ 2 Φ v
λ2 =
2
Φ uu , Φ v
Φv
,
2
λ 3 = Φ uu , N
2
.
......................................................................... (3.5)
......................................................................... (3.6)
(3.6 ) da N değerini yerine koyalım.
λ3 =
1
Φu Φv
Φ uu , Φ u Λ Φ v
veya
λ3 =
1
Φu Φv
det (Φ uu , Φ u , Φ v ) ..................................................................... (3.7)
Şimdi (3.3) de (3.4), (3.5), (3.6) ve (3.7) değerlerini yerlerine koyalım.
15
Φ uu =
Φ uu , Φ u
2
Φu
Φ uu , Φ v
Φu +
Φv
2
Φv +
1
Φu Φv
det (Φ uu , Φ u , Φ v ) N ........... (3.8)
bulunur.
Φ uv = Φ vu olduğundan
Φ uv = µ1 Φ u + µ 2 Φ v + µ 3 N
......................................................................... (3.9)
burada µ1 , µ 2 ve µ 3 değerlerini bulalım.
Φ uv , Φ u = µ1 Φ u
µ1 =
2
Φ uv , Φ u
Φu
......................................................................... (3.10)
2
Φ uv , Φ v = µ 2 Φ v
µ2 =
2
Φ uv , Φ v
Φv
......................................................................... (3.11)
2
µ 3 = Φ uv , N .
......................................................................... (3.12)
(3.12 ) de N değerini yerine koyalım:
µ3 =
1
Φu Φv
Φ uv , Φ u Λ Φ v
veya
µ3 =
1
Φu Φv
det (Φ uv , Φ u , Φ v ) ....................................................................... (3.13)
16
Şimdi (3.9) da (3.10) , (3.11) ve (3.13) değerlerini yerlerine koyalım.
Φ uv =
Φ uv , Φ u
Φu
2
Φu +
Φ uv , Φ v
Φv
2
Φv +
1
Φu Φv
det (Φ uv , Φ u , Φ v ) N ..... (3.14)
bulunur.
Φ vv = ν 1 Φ u + ν 2 Φ v + ν 3 N ,
......................................................................... (3.15)
burada ν 1 , ν 2 ve ν 3 değerlerini bulalım:
Φ vv , Φ u = ν 1 Φ u
ν1 =
,
Φ vv , Φ u
Φu
......................................................................... (3.16)
2
Φ vv , Φ v = ν 2 Φ v
ν2 =
2
2
,
Φ vv , Φ v
Φv
......................................................................... (3.17)
2
ν 3 = Φ vv , N .
......................................................................... (3.18)
(3.18) de N değerini yerine koyalım:
ν3 =
1
Φu Φv
Φ vv , Φ u Λ Φ v
veya
ν3 =
1
Φu Φv
det (Φ vv , Φ u , Φ v ) ................................................................... (3.19)
17
Şimdi (3.15) de (3.16) , (3.17) ve (3.19) değerlerini yererine koyalım.
Φ vv , Φ u
Φ vv =
Φu +
2
Φu
Φ vv , Φ v
Φv
2
Φv +
1
Φu Φv
det ( Φ vv , Φ u , Φ v )N ...... (3.20)
bulunur.
Şimdi (3.2) de (3.8) ve (3.14) değerlerini yerlerine koyalım.
Φ uu , Φ u
dN
=
3
du
Φu Φv
+
1
2
Φu
Φv
+ Φu Λ Φu
+
2
Φu
Φv
Φu
- Φu Λ Φv
2
Φ uu , Φ v
Φu Φv
3
Φv Λ Φv
det ( Φ uu , Φ u , Φ v )N Λ Φ v
Φ uv , Φ u
1
2
Φu Λ Φv +
3
Φv
+ Φu Λ Φv
Φ uv , Φ v
Φu Φv
3
det ( Φ uv , Φ u , Φ v ) Φ u Λ N
Φ uu , Φ u
Φu
3
Φv
- Φu Λ Φv
Φ uv , Φ v
Φu Φv
3
Gerekli kısaltmalar yapılınca :
1
dN
=det ( Φ uu , Φ u , Φ v ) Φ u
3
du
Φu Φv
-
1
Φu Φv
3
det ( Φ uv , Φ u , Φ v ) Φ v ........................................................... (3.21)
18
Şimdi (3.1) de (3.21) değerini yerine koyalım :
1
S (V1) = -
Φu
4
det ( Φ uu , Φ u , Φ v ) Φ u
Φv
1
-
Φu
2
Φv
3
det ( Φ uv , Φ u , Φ v ) Φ v
veya
S (V1) = -
1
Φu
3
det ( Φ uu , Φ u , Φ v )V1
Φv
1
-
Φu
2
Φv
2
det ( Φ uv , Φ u , Φ v )V2
bulunur. Şimdi benzer biçimde S(V2) yi hesaplayalım :
S(V2) = D V2 N
S(V2) = D
1
Φv
Φv
N
S(V2) =
1
D Φv N ,
Φv
S(V2) =
1 dN
Φ v dv
O halde
......................................................................... (3.22)
dN
yi hesaplayalım:
dv
19
Φ uv , Φ u
dN Φ uv Λ Φ v + Φ u Λ Φ vv
=
- Φu Λ Φv
3
Φu Φv
dv
Φu Φv
Φ vv , Φ v
- Φu Λ Φv
Φu Φv
3
. ......................................................................... (3.23)
Şimdi (3.23) de (3.14) ve (3.20) değerlerini yerlerine koyalım,
Φ uv , Φ u
dN
=
3
dv
Φu Φv
Φ vv , Φ u
3
Φu
Φu
3
Φv Λ Φv
2
Φv
2
Φ vv , Φ v
Φu Φv
3
Φu Λ N
Φu
Φ uv , Φ u
3
Φu
+ Φu Λ Φv
Φv
+ det ( Φ vv , Φ u , Φ v )
- Φu Λ Φv
Φu Φv
N Λ Φv
+ det ( Φ uv , Φ u , Φ v )
+ Φu Λ Φu
Φ uv , Φ v
Φu Λ Φv +
Φv
-
2
Φv
2
Φu Λ Φv
Φ vv , Φ v
Φu Φv
3
ve gerekli kısaltmalar yapılırsa,
1
dN
= det ( Φ uv , Φ u , Φ v ) Φ u
3
dv
Φu Φv
-
1
Φu Φv
3
det ( Φ vv , Φ u , Φ v ) Φ v . .................................................... (3.24)
20
Şimdi (3.22) de (3.24) değerini yerine koyalım.
S (V2) = -
-
1
3
Φu
1
det ( Φ vv , Φ u , Φ v ) Φ v
4
Φu Φv
det ( Φ uv , Φ u , Φ v ) Φ u
2
Φv
veya
S (V2) = -
1
2
Φu
2
Φv
1
-
Φu Φv
det ( Φ uv , Φ u , Φ v ) V1
det ( Φ vv , Φ u , Φ v ) V2
3
bulunur.
S (V1) = aV1 + bV2
S (V2) = cV1 + dV2
Olduğundan
aV1 + bV2 = -
-
cV1 + dV2 = -
1
Φu
3
Φv
det ( Φ uu , Φ u , Φ v ) V1
1
Φu
2
Φv
2
det ( Φ uv , Φ u , Φ v ) V2 ,
2
det ( Φ uv , Φ u , Φ v ) V1
1
Φu
2
Φv
21
1
-
Φu Φv
3
det ( Φ vv , Φ u , Φ v ) V2
olur. Bu taktirde,
a=-
b=-
c=-
d=-
1
3
Φu
det (Φ uu , Φ u , Φ v )
Φv
1
Φ
2
u
2
Φ
1
Φu
2
Φv
2
1
Φu Φv
det ( Φ
uv
,Φ
u
,Φ v )
v
3
det (Φ uv , Φ u , Φ v )
det (Φ vv , Φ u , Φ v )
elde edilir.
a b 
S= 

c d 
1

det(Φuu , Φu , Φv )
3

Φ
Φ
u
v


S= 

1
det(Φuv , Φu , Φv )
−
2
2
 Φu Φv

det(Φuv , Φu , Φv ) 
Φu Φv


 ..... (3.25)

1
−
det
(
Φ
,
Φ
,
Φ
)
vv
u
v 
3
Φu Φv

−
1
2
2
bulunur.
Diğer taraftan I.hale göre yüzeyin parametre eğrileri eğrilik çizgileri ise:
Eğrilik çizgisi tanımından
22
S( Φ u ) = λΦ u
veya
S(V1) = λ ' V1 ,
S( Φ v ) = µΦ v
veya
S(V2) = µ' V2
olacaktır.
Buna gore S(V1) in ifadesindeki V2 nin katsayısı ve S(V2) de V1 in katsayısı 0 olacaktır.
Bu da det ( Φ uv ' Φ u , Φ v ) = 0 olmasını gerektirir.
Böylece, b = c = 0 olacaktır.
O halde I. haldeki yüzeyler için Weingarten dönüşümünün matrisi şu şekildedir:
1

det (Φ uu , Φ u , Φ v )
3
−
Φ
Φ
v
u

S = 


0





 ....... (3.26)


det (Φ vv , Φ u , Φ v )

0
−
1
Φu
Φv
3
(Sağel 1979).
II. Hal : Yüzeyin eğrilik çizgileri parametre eğrileri değil ise :
(u,v)
→
(u ′ , v ′)
biçiminde bir parametre değişimi yapmak suretiyle (u,v)
parametrelerine göre eğrilik çizgisi olmayan parametre eğrileri bırakılarak (u ′ , v ′) yeni
parametreler esas alınır, öyle ki (u ′ , v ′) parametrelerine göre eğrilik çizgileri parametre
eğrileri olurlar. Bu durumda I. haldeki S matrisi doğrudan doğruya alınabilir. Fakat
çoğu zaman (u,v) → (u ′ , v ′) dönüşümü yüzeyin denklemini karışık ifadelere getireceği
için gerekli türevleri hesaplamak zorluk arzeder. Bu nedenle (3.25) i uygularsak daha
yararlı olur (Sağel 1979).
23
→ E3
Örnek 3.2.1: Φ : E2 
(u,v) 
→ Φ (u,v) = (cosucosv, cosusinv, au)
biçiminde verilen M yüzeyinin Weingarten dönüşümünün matrisini hesaplayalım.
Φ (u,v)= (cos u cos v, cos u sin v, au ) ‘nun u ya ve v ye göre türevlerini alalım.
Φ u = (− sin u cos v,− sin u sin v, a )
Φ v = (− cos u sin v, cos u cos v,0 )
olsun.
Φu ,Φv = 0
olduğundan {Φ u , Φ v } sistemi χ (M) için ortogonal bir bazdır.
Normlarsak,
1
V1 =
Φu
=
Φu
V2 =
Φv
= (− sin v, cos v,0 )
Φv
2
a + sin 2 u
(− sin u cos v,− sin u sin v, a )
{V1 , V2} sistemi χ (M) için bir ortonomal baz olur. M yüzeyinin birim normal vektörü
N= V1 ∧ V2
N=
1
a 2 + sin 2 u
(−a cos v,−a sin v,− sin u )
dir.
24
S(V1)= D V1 N
S(V2)= D V2 N dir.
Φ u ≠ 1 olduğundan M üzerindeki u= sabit parametre eğrisinin yay uzunluğu u
değildir, bu yay uzunluğu s1 ile gösterirsek
S(V1)= D V1 N =
dN dN du
=
ds1 du ds1
dir. Burada u= sabit parametre eğrisini
Φ : I →M
u → Φu
ile gösterirsek
V1 =
dΦ dΦ du
=
ds1 du ds1
olur. Buradan normlayarak
1= V1 = Φ s1 = Φ u
du
ds1
veya
1
du
=
ds1 Φ u
bulunur. O halde ,
25
S(V1)=
dN 1
du Φ u
olur. Benzer şekilde
S(V2)=
dN 1
dv Φ v
bulunur. Buna göre
S(V1)=
a cos u
( − sin u cos v,− sin u sin v, a )
(a + sin 2 u ) 5 / 2
S(V1)=
a cos u
Φu
(a + sin 2 u ) 5 / 2
S(V1)=
a cos u
V1
(a + sin 2 u ) 3 / 2
2
2
2
olur. Benzer şekilde
S(V2)=
a
2
cos u a + sin 2 u
V2
bulunur. Böylece,
a cos u

 (a 2 + sin 2 u ) 3 / 2

S= 


0





 bulunur.


a

cos u a 2 + sin 2 u 
0
Şimdi de Bölüm 3.2’de elde edilen yöntemle şekil operatörünü hesaplayalım.
Φ (u,v) = (cosucosv, cosusinv, au) nin u ya ve v ye göre türevlerini alalım.
26
Φ u =(-sinucosv, -sinusinv, a)
Φ v =(-cosusinv, cosucosv, 0)
Φu ,Φv = 0
Φ uv = (sinusinv, -sinucosv, 0)
det( Φ uv, Φ u, Φ v) = 0 olduğundan matris hesabında 1. durum sözkonusudur.
Φ uu ve Φ vv yi hesaplayalım.
Φ uu = (-cosucosv, -cosusinv, 0)
Φ vv = (-cosucosv, -cosusinv, 0)
− cos u cos v − cos u sin v 0
det (Φ uu , Φ u , Φ v ) = − sin u cos v − sin u sin v a = acos2u
− cos u sin v cos u cos v 0
Burada Φ uu = Φ vv olduğundan
det (Φ uu , Φ u , Φ v ) = det (Φ vv , Φ u , Φ v ) = acos2u
Φu =
Φu
3
a 2 + sin 2 u
= (a 2 + sin 2 u )
3
2
Φ v = cosu
Φv
3
= cos3u
Şimdi bulduğumuz değerleri Weingarten dönüşümünün matrisinde yerine yazalım:
27
a cos u

 2
2
 a + sin u
S= 


0


(
)
3



 bulunur.


a

cos u a 2 + sin 2 u 
0
2
3.3 Gauss Dönüşümü ve Gauss Eğriliği ile Şekil Operatörü Arasındaki İlişki
En de bir hiperyüzey M ve bir (n-1) hiperküre Sn-1 olmak üzere
η :M
→ Sn-1 ⊂ E n
n
P
→ η(P) = N ( P) = (P, N P ) =
∂
∑ a (P) ∂x
i
i =1
P
i
biçiminde tanımlanan ve M yi En deki Sn-1 birim hiperküresine resmeden Gauss
dönüşümünü ele alırsak,
→ T n −1 ( η (P))
η* : TM(P) 
S
lineer dönüşümü için
η* =S(P)
olduğunu biliyoruz. Ayrıca TMP deki lineer bağımsız Φ ={X1,X2,…,Xn-1} sistemi için
det( η* (X1), η* (X2), … , η* (Xn-1))=det η* . det(X1, X2, …, Xn-1) dir.
Burada
det η* = detS(P) = K(P) dir.
M nin P deki hiperhacim elementi (alan elementi)
dV = det(X1,X2,…,Xn-1)
ve
28
Sn-1 in η(P) noktasındaki hiperhacim elementi
d V = det( η* (X
 1), η* (X2),…, η* (X
 n-1))
d V =K(P) . dV
K(P)=
olmak üzere
veya
hiperküresel alan elementi
dV
=
dV hiperyüzeyin alan elementi
bulunur (Hacısalihoğlu 1994).
Sonuç 3.3.1: En deki bir M hiperyüzeyinin bir P noktasındaki Gauss eğriliği, M nin
küresel resminin η (P) deki hiperalan elementinin P deki hiperalan elementine oranıdır.
3.4 En de Bazı Özel Yüzeyler İçin Şekil Operatörü, Temel Formlar, K ve H
Fonksiyonları
3.4.1 Hiperdüzlemler için şekil operatörü, temel formlar, K ve H fonksiyonları
Tanım 3.4.1.1: En n boyutlu Öklid uzayının (n-1) boyutlu bir hiperdüzlemi M olsun.
n


M= x x = (x 1 , x 2 , ..... , x n ), f ( x ) = ∑ a i x i − b = 0 , ∇f ≠ 0
i =1


dir ve En deki bir nokta cümlesidir. M üzerinde birim normal vektör alanı N ise
a1, a2, … , an ∈ C ∞ (M, IR) ve ai = sabit olmak üzere
n
N= (a1, a2, … , an) =
∑a
i =1
i
∂
∂x i
yazılabilir (Hacısalihoğlu 1994).
Hiperdüzlem için Şekil Operatörü:
∀X ∈ χ (M ) için,
S(X) = DXN
29
n
=
∑ X[a ]
i
i =1
∂
∂x i
⇒ S(X) = 0 ⇒ S = 0
dır. O halde şu sonuç yazılabilir:
Sonuç 3.4.1.1: En , n boyutlu Öklid uzayının her bir hiperdüzleminin Weingarten
dönüşümü, sıfır dönüşümüdür (Hacısalihoğlu 1994).
Hiperdüzlem için Temel Formlar:
S ≡ 0 olduğundan k ≠ 0 olmak üzere , ∀k ∈ IN için
S k (X) , Y = 0, Y = 0
olacaktır. Buna göre, şu sonuç yazılabilir.
Sonuç 3.4.1.2: En, n boyutlu Öklid uzayının (n-1) boyutlu bir hiperdüzlemi üzerinde,
birinci temel form hariç, diğer bütün temel formlar singülerdir, yani (0) dır
(Hacısalihoğlu 1994).
Hiperdüzlem İçin K ve H Eğrilik Fonksiyonları:
S ≡ 0 olduğundan M nin bütün noktalarında S nin karakteristik değerleri, k1, k2 birer 0
reel sayısından ibaret olacaktır. Bu nedenle M üzerinde her nokta için;
K = k1 k2 = H = k1 + k2 = 0
olur.
Sonuç 3.4.1.3: En ,n boyutlu Öklid uzayının (n-1) boyutlu bir hiperdüzleminin bütün
noktalarında K total eğriliği, H ortalama eğriliği ve dolayısıyla bütün diğer eğrilikler
özdeş olarak sıfırdır (Hacısalihoğlu 1994).
3.4.2 Hiperküre için şekil operatörü, temel formlar, K ve H fonksiyonları
Tanım 3.4.2.1: En n boyutlu Öklid uzayında
30
n
x = (x 1 , ..., x n ) f ( x ) = ∑ x i2 = r 2 , ∇ f ≠ 0 , r ∈ IR , r = sabit
{
S nr −1 =
}
i =1
nokta cümlesine bir (n-1) boyutlu hiperküre veya kısaca (n-1) küre denir. Burada r
hiperkürenin yarı çapını göstermektedir.
P = (P1 , P2, …,Pn) ∈ S nr −1 ve N de S nr −1 in dış birim normal vektör alanı olsun.
O zaman,
NP =
1
r
n
∑
Pi
İ =1
∂
∂x i
P
dir (Hacısalihoğlu 1994).
Hiperküre İçin Şekil Operatörü :
S nr −1 in küresel dönüşümünü gözönüne alacağız.
η : S nr −1 
→ S 1n −1
P 
→ η (P ) = (
1
1
P 1 , . . . , Pn )
r
r
idi. Şimdi, η ∗ dönüşümünü hesaplayalım. S nr −1 üzerinde bir lokal koordinat komşuluğu
{x 1 ,..., x n −1 }olsun.
η∗ (
∂
∂x 1
P
)
, 1 ≤i ≤ n −1
tanjant vektörünü bulacağız.
(η ∗ (
∂
∂x i
P
) ) (xj) =
∂ ( x j oη )
∂x i
1
∂( x j)
r
=
∂x i
η (P) ,
1 ≤ i, j ≤ n − 1 ,
η (P)
31
=
1 ∂
r ∂x i
η (P)
(xj) .
İki fonksiyonun eşitliği tanımından
η∗ (
∂
∂x i
P
1 ∂
r ∂x i
)=
η (P)
, 1 ≤ i ≤ n −1
1
∀X ∈ χ (S nr −1 ) , η ∗ (X)= X
r
Diğer taraftan,
S(X)=η ∗ (X )
dır. O halde,
1
∀X ∈ χ (S nr −1 ) , S(X)= X
r
yazılabilir. Böylece,
1
S= I n −1
r
elde edilir (Hacısalihoğlu 1994).
Hiperküre İçin Temel Formlar:
1
1
S= I ⇒ S k = k I ⇒
r
r
I ( k +1) =
1
I,
rk
dır. Eğer, (n-1) kürenin yarıçapı r = 1 alınırsa, bütün temel formlar birinci temel forma
eşit olur. Herhangi r ∈ IR için k-ıncı temel form olarak
(kI) (X,Y) =
1
r
k −1
X, Y
32
yazılabilir (Hacısalihoğlu 1994).
Hiperküre İçin K ve H Eğrilik Fonksiyonları:
1
S= I olduğundan, S nin karakteristik değerleri olan k i , 1 ≤ i ≤ n − 1 fonksiyonları için
r
ki=
1
, 1 ≤ i ≤ n −1 ,
r
yazılabilir. Dolayısıyla,
n −1
1
K= ∏ k i = ( ) n −1
r
i =1
n −1
H= ∑ k i =
i =1
n −1
r
dir (Hacısalihoğlu 1994).
Sonuç 3.4.2.1: n boyutlu Öklid uzayının bir (n-1) küresi üzerindeki bütün noktalarda
total eğrilik K=
1
r
n −1
1
ve ortalama eğrilik H= (n − 1) dir (Hacısalihoğlu 1994).
r
3.4.3 Hipersilindir için şekil operatörü, temel formlar, K ve H fonksiyonları
Tanım 3.4.3.1: E n , n boyutlu Öklid uzayında bir (n-1) boyutlu hipersilindir
C= {( x 1 , x 2 ,..., x n )
n −1
xi ∈ IR , 1 ≤ i ≤ n ,
∑x
2
i
=1
}
i =1
biçiminde bir nokta cümlesidir. Bu silindir için kısaca bir (n-1) silindir de denir.
C (n-1) silindirinin dış normallerini, C üzerindeki birim normal vektör alanı olarak
düşünebiliriz. Buna göre, P= (p1,…,p n ) ∈ C için
N P =(p 1 ,p2,…,p n −1 ,0)
33
şeklinde tanımlı N vektör alanı, C nin birim normal vektör alanıdır. Üstelik,
N, e n = 0
dır (Hacısalihoğlu 1994).
(n-1) Silindir İçin Şekil Operatörü:
E n in {x 1 , x 2 ,..., x n } Öklid koordinat sistemini gözönüne alalım. Bu sisteme göre C
silindiri yukarıda tanımlandığı gibi olsun. O zaman, C nin, birim normal vektör alanı
n −1
∂
∂x i
N= ∑ x i
i =1
şeklindedir. Şimdi, χ (C) nin bir bazında S nin alacağı değerleri bulacağız.
Silindirin ekseni e n =
∂
∂
olduğundan,
∈ χ (C)
∂x n
∂x n
dir. Halbuki,
S(
∂
) =D ∂ N
∂x n
∂x
n
S(
S(
n −1
∂
) =
∂x n
∂
∂
∑ ∂x [x ] ∂x
∂
) =
∂x n
∑ ∂x
⇒S = (
i
i =1
n
n −1
∂x i
i =1
n
.
i
∂
∂x i
∂
) =0 dir.
∂x n
 ∂ 

 sistemini, (n-1) boyutlu vektör uzayı olan χ (C) nin bir bazına tamamlayalım.
 ∂x n 
Bu baz,
34
 ∂

, x 1 , x 2 ,..., x n − 2 

 ∂x n

olsun. Diğer taraftan,
n −1
X k = ∑ ξ kj
j=1
∂
∂x j
şeklindedir. Halbuki, S(X k ) = D X k N olduğundan,
n −1
S(X k ) =
∑ X [x ]
i
k
i =1
n −1
n −1
i =1
j=1
S(X k ) = ∑ ( ∑ .
n −1
⇒ S (X k ) = ∑ ξ kj
j=1
∂
∂x i
∂x i
∂
ξ kj )
∂x j
∂x i
∂
∂x j
⇒ S (X k ) = X k
 ∂

olur. O halde, χ (C) nin 
, x 1 , x 2 ,..., x n − 2  bazı için,
 ∂x n

 ∂
S 
 ∂x n

 = 0

S (X k ) = X k , 1 ≤ k ≤ n − 2
elde edilir.
Geometrik açıdan {x 1 ,..., x n −2 } sistemini şu şekilde yorumlayabiliriz:
35
n −1


C= (x 1 ,..., x n −1 , x n ) x i ∈ IR ,∑ x i2 = 1
i =1


silindirinde, ∀P = ( P1 , P2 ,..., Pn −1 , Pn ) ∈ C noktası için ilk (n-1) tane bileşenin kareleri
toplamı 1 dir. O halde, n-yinci bileşenin her keyfi ve sabit değeri için E n in
(n-2) hiperküresi elde edilir. Diğer taraftan, bu küre S n − 2 ile gösterilirse χ (S n − 2 ) ile
 ∂ 
n −2

 in ortogonal ve χ(S ) ∈ χ (C ) olacağı açıktır. O halde,
∂
x
 n
S P {x 1 ,..., x n − 2 } = χ (S n − 2 )
olacaktır. Daha açık olarak, C nin
∂
ye dik her bir (n-1) hiperdüzlemi ile arakesiti
∂x n
olan (n-2) kürenin vektör alanlarının vektör uzayı,
S p {x 1 ,..., x n − 2 }
dir.
 ∂

Böylece, Φ = 
, x 1 ,..., x n − 2  bazına göre S nin matrisi de,
 ∂x n

0
Φ = 
0

 dir (Hacısalihoğlu 1994).

I n −2 
0
Silindirin Üzerinde Temel Formlar:
0
S Φ = 
0



I n −2 
0
36
olduğu gözönüne alınırsa, ∀ k ∈ IN , k ≠ 0 için,
Sk = S
ve k = 0 için
S0 = I
elde edilir. Buna göre şu sonuç yazılabilir:
Sonuç 3.4.3.1: n boyutlu Öklid uzayının bir (n-1) hipersilindirinin, birinci temel formu
hariç diğer bütün temel formları, ikinci temel forma eşittir (Hacısalihoğlu 1994).
Silindirin Kve H Eğrilik Fonksiyonları:
0
S Φ = 
0



I n −2 
0
olduğundan, S nin karakteristik değerleri,
k 1 = 0 , k 2 = k 3 = k n− 2 = 1
ve
K = detS = detS Φ = 0
H = izS = izS Φ = (n-2)
dir. Böylece şu sonuç yazılabilir:
Sonuç 3.4.3.2: M boyutlu Öklid uzayında, bir (n-1) hipersilindirin, bütün noktalarında
total eğrilik K = 0 ve ortalama eğrilik H = (n-2) dir (Hacısalihoğlu 1994).
37
3.4.4 Dönel yüzeyler için şekil operatörü, K ve H fonksiyonları
E 2 de bir açık aralık A ve
Φ: A
→ E 3
(u , v) 
→ Φ ( u , v ) = (f (u , v ), g (u , v ), h (u , v )) ve burada f, g, h
reel değerli
fonksiyonlardır.
T u = (f u , g u , h u ) ,
fu =
∂f
∂g
, gu =
∂u
∂u
,
hu =
∂h
∂u
T uu = (fuu , guu , huu)
T uv = (fuv , guv , huv)
T vv = (fvv , gvv , hvv)
yazabiliriz.
 ∂ 
Burada T u = Φ ∗   , Φ ( A ) üzerindeki u parametreli eğrilere diktir.
 ∂u 
Kabul edelim ki T u x Tv ≠ 0 olsun. Böylece Φ , A dan E 3 e bir immersiyon olur.
N=
Tu x Tv
W
,
W=
T u x TV
≠ 0 olsun.
N ye bağlı S Weingarten dönüşümünü hesaplamak için
S (Tu ) = D Tu N = N u olduğundan
< S (Tu ) , Tu > = < N u Tu > = − < Tuu , N > dir.
38
Benzer biçimde < S ( T i ) , T j > = - < T ij , N > i ve j ye bağlı olarak bulunur.
Eğer T u ve T v ortogonal ise
K=
< Tuu , N > < Tvv , N > − < Tuv , N > 2
< Tu , Tu > < Tv , Tv >
 < T , N > < Tvv , N > 
H = −  uu
+

 < Tu , Tu > < Tv , Tv > 
ve
(Hicks 1974).
39
4. ŞEKİL OPERATÖRÜ (WEINGARTEN DÖNÜŞÜMÜ) VE TEMEL
FORMLARLA İLGİLİ LORENTZ UZAYINDA YAPILAN ÇALIŞMALAR
4.1 Lorentz Uzayında Dönel Yüzeyin Weingarten Dönüşümünün Matrisinin
Hesabı ile Gauss ve Ortalama Eğriliklerinin Hesaplanması
Bu bölümde amacımız Bölüm 3.4.4’de verilen dönel yüzeylerin Weingarten
dönüşümünün matrisinin hesabını Lorentz uzayı için genişletmektir.
M, L 2 de bir açık aralık olsun ve,
Φ:M 
→ L3
→ Φ (u , v ) = (Φ 1 (u , v ) , Φ 2 (u , v ) , Φ 3 (u , v ))
(u,v) 
( (u , v ) ∈ M , Φ 1 , Φ 2 , Φ 3 reel değerli fonksiyonlar olmak üzere )
T u = (Φ 1u , Φ 2 u , Φ 3u ) ,
Φ 1u =
∂Φ 1
∂Φ 2
, Φ 2u =
∂u
∂u
, Φ 3u =
∂Φ 3
,
∂u
T uu = (Φ 1uu , Φ 2 uu , Φ 3uu ) ,
T uv = (Φ 1uv , Φ 2 uv , Φ 3uv ) ,
T vv = (Φ 1vv , Φ 2 vv , Φ 3vv )
yazabiliriz.
 ∂ 
T u = Φ ∗   nun Φ(M ) üzerindeki u parametreli eğrilere dik olduğuna dikkat ediniz.
 ∂u 
Kabul edelim ki T u ∗ Tv ≠ 0 olsun. Böylece Φ , M den L3 e bir immersiyon olur.
N=
Tu ∗ TV
Tu ∗ Tv
(
Tu ∗ Tv
L
≠ 0 için ) olsun.
L
40
N’ye bağlı S Weingarten dönüşümünü hesaplayalım:
S (Tu ) = D Tu N = N U olduğunu biliyoruz.
< S (Tu ), Tu >
< N , Tu >
⇒ < N u , Tu >
L
L
L
= < N u , Tu >
=0 ⇒
L
………………………………………(4.1)
∂
< N , Tu > L = < N u ,Tu >
∂u
= − < N , Tuu >
L
L
+ < N , Tuu > = 0
………………………………………(4.2)
Buradan;
< S (Tu ), Tu >
L
= − < N , Tuu >
L
< S (Tv ), Tv >
L
= − < N , Tvv >
L
< S (Tu ), Tv >
L
= − < N , Tuv >
L
< S (Tv ), Tu >
L
= − < N , Tvu >
L
Benzer olarak;
= − < N , Tuv >
L
.
Tu ve Tv nin ortogonal olması durumunda ve
S(Tu) = aTu + bTv
S(Tv) = cTu + dTv
………………………………………(4.3)
iken a, b, c ve d yi bulmaya çalışalım. (4.3) eşitliğinden
Tu
2
L
= − < Tu ,Tu >
L
41
Tu
2
Tu
2
i)
L
=< Tu , Tu >
L
=0
iv)
< S(Tu ) , Tu >
< Tu , Tu >
L
2
=m
L
2
L
=m
L
Tv
L
Tu
L
Tv
2
L
L
2
L
= ± c Tu
2
L
L
2
L
= ± d Tv
< N , Tvv >
L
L
= ± b Tv
< N , Tuv >
= d < Tv , Tv >
L
L
< N , Tuv >
L
2
2
Tu
= c < Tu , Tu >
L
< S(Tv ) , Tv >
Tv
=m
= ± a Tu
< N , Tuu >
L
< S (Tv ), Tv >
d= ±
L
2
< S(Tv ) , Tu >
Tu
=m
L
< S(Tu ) , Tv >
Tv
L
L
= b < Tv , Tv >
L
< S (Tv ), Tu >
c= ±
= a < Tu , Tu >
L
< S (Tu ), Tv >
b= ±
iii)
değerlerini alabilir.
< S (Tu ), Tu >
a= ±
ii)
L
2
L
L
2
L
a, b, c ve d katsayılarını Weingarten dönüşümünün matrisinde yerine yazarsak
 < N , Tuu >
m
2
Tu L

S = 
 < N , Tuv >
m
2

Tu L
L
L


2
Tv L 


< N , Tvv > L 

m
2
Tv L 
m
< N , Tuv >
42
L
Weingarten dönüşümünün matrisini kullanarak Lorentz uzayının Gauss ve Ortalama
eğriliklerini hesaplayalım.
K = det S
 < N , Tuu >
K= m 

L
< N , Tvv >
Tu
2
L
+
L
Tv
L
2
− < N , Tuv > 2
L
L



H = iz S
 < N , T uu >
H= m 
2

Tu
L
< N , T vv >
Tv
L
2
L



(Sağel 1998).
4.2 Lorentz Uzayında Temel Formlar ile Dönel Yüzeyin Ortalama Eğriliği
Arasındaki Bağıntı
Teorem 4.2.1: Lorentz uzayında temel formlar ile dönel yüzeylerin ortalama
eğrilikleri arasında
H=m
III (X p , Yp )
II (X p , Yp )
bağıntısı vardır.
İspat: Lorentz uzayındaki dönel yüzeyin S şekil operatörünün karakteristik
polinomu
PS (λ ) = det(S − λI 2 ) olsun.
 < N ,Tuu >
PS (λ) = λ2 ± 
2
 Tu L
L
+
< N ,Tvv >
Tv
2
L
L

λ

 < N ,Tuu > L < N , Tvv > L − < N ,Tuv >2
m 
2
2

Tu L Tv L
43
L



< N ,Tuu >
PS (S) = S 2 ± 
2
 Tu L
L
+
< N ,Tuv >
Tv
2
L
L

S

< N ,Tuu > L < N ,Tvv > L − < N ,Tuv >2
m 
2
2

Tu L Tv L
L

 =0

olduğundan (Cayley-Hamilton Teoremi)
∀X p , Yp ∈TM (P) için
 < N , Tuu >
< S (Xp ) , Yp > ± 
2
 Tu L
2
L
+
< N , Tvv >
Tv
L
2
L
 < N ,Tuu > L < N ,Tvv > L − < N , Tuv >2
m
2
2

Tu L Tv L
L

 < S(Xp ) , Yp >


 < Xp , Yp > = 0

Temel formun tanımından
I(Xp , Yp) = < Xp , Yp > = 0
(Xp , Yp ∈TM (P) )
II(Xp , Yp) = < S(Xp) , Yp >
III(Xp , Yp) = < S2(Xp) , Yp >
O halde,
 < N , Tuu >
III(Xp , Yp) ± 
2
 Tu
L
L
+
< N , Tvv >
Tv
2
L
44
L

 II X p , Y p = 0

(
)
 < N , Tuu >
⇒
2
 Tu L
L
+
< N , Tvv >
Tv
2
L
L

III(X p , Yp )
 =m
II(X p , Yp )

H = =m
III(X p , Yp )
II(X p , Yp )
45
(Sağel 2002).
KAYNAKLAR
Hacısalihoğlu, H. H., 1994, Diferensiyel Geometri. II. Cilt. Ankara Üniversitesi Fen
Fakültesi Yayınevi, 339, Ankara
Hacısalihoğlu, H. H., 1982. Lineer Cebir. Fırat Üniversitesi Fen Fakültesi Yayınları
No:3, Elazığ
Hicks, N. J., 1974. Notes on Differential Geometry. Van Nostrand Reinhold Company,
London
Kühnel, W., 2006. Differential geometry: curves-surfaces-manifolds (translated by
Bruce Hunt). Providence, R. I. : American Mathematical Society, 380,
New York
Richard, S. M., Parker, G. D., 1977. Elements of Differantial Geometry. Prentice-Hall
Inc. Engelwood Cliffs, New Jersey
Sağel, M. K., 1979. Weingarten Dönüşümü ve Yüzeylerin Diferensiyel Geometrisi.
Yüksek Lisans Tezi, Dicle Üniversitesi, Diyarbakır
Sağel, M. K., 1998. On the curvature of surface of revolution in Lorentz Space. Bull.
Call. Math. Soc: 90, 89-94
Sağel, M. K., 2002. The Relationships between the fundamental forms with the mean
curvature of a surfaces of revolution in the Lorentz Space. Journal of Ins.
Of Math & Comp. Sci. (Math. Ser.) Vol: 15, No: 3, 213-215
Tsagas, G., Parantoniov, B., 1988. On the Rectilinear congruences of Lorentz Manifold
establishing an area preserving representation. Tensor N. S. Vol: 47. pp.
127-139
46
ÖZGEÇMİŞ
Adı Soyadı
: Merve BAYSAL
Doğum Yeri : İstanbul
Doğum Tarihi : 07/11/1980
Medeni Hali : Bekar
Eğitim Durumu
Lise
: Maçka Anadolu Teknik Lisesi (1994-1998)
Lisans
: İstanbul Üniversitesi Fen Fakültesi Matematik Bölümü
(1998-2003)
Yüksek Lisans
:Ankara
Üniversitesi
Fen
Anabilim Dalı (2004-2007)
47
Bilimleri
Enstitüsü
Matematik