Çoklu rasgele değişkenler, ilinti ve kovaryans kavramları, iki

1
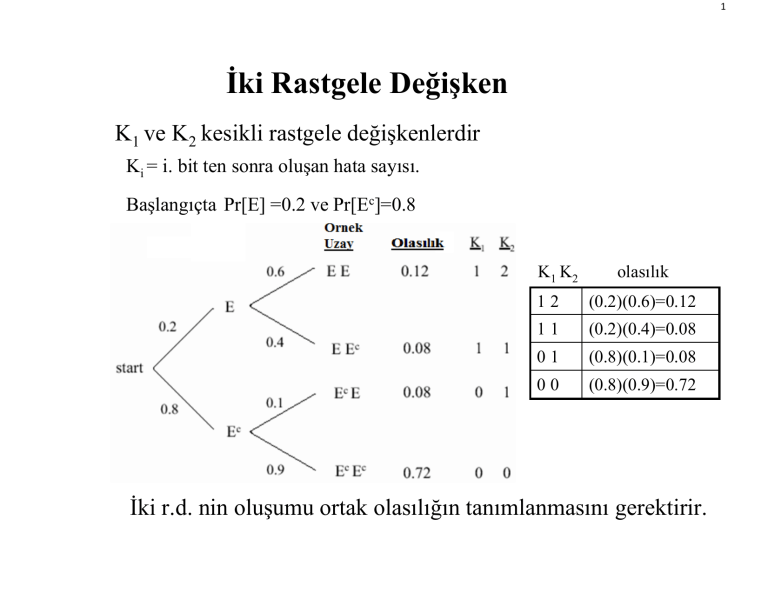
İki Rastgele Değişken
K1 ve K2 kesikli rastgele değişkenlerdir
Ki = i. bit ten sonra oluşan hata sayısı.
Başlangıçta Pr[E] =0.2 ve Pr[Ec]=0.8
K1 K2
olasılık
12
(0.2)(0.6)=0.12
11
(0.2)(0.4)=0.08
01
(0.8)(0.1)=0.08
00
(0.8)(0.9)=0.72
İki r.d. nin oluşumu ortak olasılığın tanımlanmasını gerektirir.
2
K1 K2
Ortak OKF
[k11,,kk22]] = Pr
Pr[[ K11 
ffKK11,,KK22[k
= k11 ,,KK22=kk22]]
∑∑ f
K1 , K 2
[k1 , k2 ] = 1
Marjinal OKF:
ffKK1 [[k
k11]] 
=∑
ffKK1,,KK2[k[k11,,kk2 2]]
1
kk22
1
2
probability
12
(0.2)(0.6)=0.12
11
(0.2)(0.4)=0.08
01
(0.8)(0.1)=0.08
00
(0.8)(0.9)=0.72
3
Rastgele Değişkenlerin Bağımsızlığı
İki rd bağımsız ise
f K1, K 2 [k1 , k2 ] = f K 1[k1 ]  f K 2[k2 ]
f K1 [ k1 ]
k2
0.8
0.2
0
f
K2
[ k2 ]
0
kk11 0.8
0.2
0.72
1
0.16
0.12
0.576
0.144
0.128
0.032
0.096
0.024
k1
1
0.16
0.72
0.12
2
k22
k2
k1k1
bu rd’ler bağımsız mı?
0.720
0
0.080
0.080
0
0.120
4
Şartlı OKF
[k , k ]  Pr[ K1 |Kk2 1=Kk22 ] k2 ]
f K1 |Kf K2 [k
1 ,K
12| k 21] =2Pr [ K1 = k1
Tanım:
Definition:
f K1 f, KK2 K[k[k
1 , 1k,2k]2 ]
f K1 ,fKK2 [|Kk1[k
, k12|]k2] =
f K2f[Kk2[k] 2]
1
1
2
2
2
f K1 |K 2 [k1 | 2]
fK1 K 2[ k1 |1]
fK1 K 2[ k1 | 0]
1.0
1.0
0.5
0.5
0
k1
1
∑ff
Bağıntılar:
0
k1k1
k2
[k11 | k22 ]] =11
[k
KK1 |K
1 | K22
∑ff
k2
1
K |K
[k1 | k22 ]] =??!!?
??!!?
[k
1
1 2
K1 |K
2
k1
0
k1
1
5
OKF ları için Bayes Kuralı
f K2 |K1 [kf2 | k[k
k]f
1 ]f K|1 [
1 ] [k ]
k
1
K
1
K
|K
2
f K1 , K2 [k1f | k2 ][k | k ] =
K |K
1
2
f K2 [k2f] [k ]
2
1
1
1
2
K2

2
f K2 |K1 [k2 | k1 ]f K1 [k1 ]
f

=
[k | k ]f [k ]
]
K22|K
| K11[k 22| k1 ]f
1 K1K[k
1 1 1
∑f
k1
K 2 |K1
[k2 | k1 ]f K1[k1 ]
k1
Check this out for the present example!
6
İki Rastgele Değişken
Sürekli rastgele değişkenler.
X1, X2 gibi iki rastgele değişken olsun,
Ortak oyf
2

FX1 , X 2 ( x1 , x2 )
2
∂ F
f X1 , X 2 ( x1 , x2 ) 
( x1 , x2 )
, x1x2
(
)
f X1 , X 2 x1 , x2 =
1
2
X X
Ortak kdf
Pr[XX 1≤xx,1 ,XX 2≤x x]2 
FFXX1 1, X, X2 2((xx11,,xx22))=Pr
1
2
1
2
x1x1 x2x2
) dzdz2 dz1
=  f f X1 , X(2 (zz,1 z, z)2 dz
∫ ∫
−∞ −∞
X1 , X 2
1
2
2
1
7
KDF ve OYF
8
Ortak oyf nin özellikleri
1.
∞ ∞
 
∫ ∫
−∞
 −∞

dx dx
dx = 1,
ffXX1 ,,XX2 (( xx11,, xx22)) dx
11 22  1,
1
) ≥0 0
ffXX11, X, X22((x1x,1x, 2x)2 
2
2. Pr  a1  X 1  b1 , a2  X 2  b2   
2. Pr [ a < X ≤ b , a < X ≤ b ] =
b1 b2
b b
a11 a22
1
1
1
2
2
2

∫ ∫
a1
a2
f X1 , X 2 ( x1 , x2 ) dx2 dx1
f X1 , X 2 ( x1 , x2 ) dx2 dx1
3. Pr  a1  X 1  a1  1 , a2  X 2  a2   2   f X1 , X 2 (a1 , a2 )1 2
3. Pr [ a1 < X 1 ≤ a1 + δ1 , a2 < X 2 ≤ a2 + δ 2 ] ≅ f X , X ( a1 , a2 ) δ1δ 2
1
2
Not: Benzer özellikler kesikli rastgele değişkenler için de
geçerlidir.
9
Ortak OYF’nin olasılık olarak yorumu
ffXX1 X, X2 ((xx11,,xx22))
1
2
Pr  a  X  b , a  X  b 
Pr [ a11< X 11 ≤ b11, a22 < X 22 ≤ b22]
b1 b2
 b1 b2 f X1 , X 2 ( x1 , x2 ) dx2 dx1
= ∫ a∫1 a2f X1 , X 2 ( x1 , x2 ) dx2 dx1
a1
a2
a2
b2
x2
δ1
a1
δ2
b1
x1
Pr  a1  X1  a1  1 , a2  X 2  a2   2   f X1 , X 2 (a1 , a2 )1 2
10
Marjinal oyf’ler

∞
ffXX11(( x11)) = ∫ f XX11,,XX22 (( x1 , x2 ))dx
dx22
−∞
ff X ((x22 )) =
dx11
X 22
∫ f XX11,,XX22 (( x11 , x22 ))dx

∞
−∞
Hatırlatma:
∞


∞
 = f ( fx )dx
)1dx = 1
 ∫ ff X ( x( x)dx
x
(
1 ) dx
1
X
2
2
∫

−∞
X1
1
1
1

X2
−∞
2
2
2
11
Marjinal oyf’nin projeksiyon olarak yorumu:
ff XX1 ((xx11))
1
f X1X 2 ( x1 , x2 )
x2
x1
X1
∞
f X1 ( x1 ) fX1 ( x1f)X1=, X 2 (−∞
x1 , fxX2 1),dx
X 2 2( x1 , x2 ) dx2


∫
12
Örnek:
 x 2 x

⎧cece− x1 ee−2 x2 ,, 00 ≤ x1 ≤ x2 < ∞
f Xf 1XX ,2X( x(1x,1x, 2x)2 )=⎨
diğer
otherwise
⎩0, 0,
1
1
2
2
(a) c nedir?
x2 x2
∞
 x1 2 x2

∞
(
 x2
2 x2
1  c   e e− x1 dx1dxdx

c
(1

e
)
e
dx
=
c
1
− edx− x22
2 1 2
1 = c0 0 e e
∫∫
0 02 x2
3−2
x2 x2
e
e 
1 c



2

3

0
c
 1 ⎡ e−2 x2c  6e −3 x2
−
16 = c
⎢
⎣−2
c
=1
⇒
0
∫
dx2
−2 x2
0
⎤
⎢
)e
∞
6
13
Örnek: (devam)
0≤ x ≤ x <∞

2 xx22
− x11 −2

⎧6e
6e e ,, 0  x1  x2  
f X11X, X22((xx11,, xx22)) = ⎨
diğer
otherwise
⎩0, 0,
x1 ) nedir?
(b) f X1 ( x1f)'i
bulun
(b)
X1 (
∞
− x −2 x
3 x−3 x1
f X 1f X( x(1x)1=
dx2 2=3e3e
) 66∫ee  x1 ee 2 x 2dx
, , 0  x01 ≤

x1 < ∞
1
2
1
1
x1x1
(c)Find
f X 2 ( x2f)'yi
bulun
(c)
X 2 ( x2 )
x2
f X1 ( x1 )  6  e  x1 e 2 x2 dx1  6e 2 x2 (1  e x2 ),
x2
0
0  x2  
14
Ortak kdf’nin özellikleri
1.1. FFXX1 1,,XX2 2(
, 
) ) =
FXF
(
, x2 ) x2 )F=
−∞
( −∞,
( −∞,
( x1), −∞0 ) = 0
X1 , F
X 2X(1,xX1 ,2 
1 , X 21, X 2
FFXX1 , X, X2 (
, ∞
) ) 1= 1
( ∞,
1
2
2. Marginal cdfs
2. Marjinal kdf ler
( x1), ∞ )
1) =
X 1, (X x
FFXX1 1( (x1x)=
FXF
2 ,
,
X
1
1
2
F
) =FXFX, X1, X(2(,∞,
FXX 2 ((xx22)=
x2 )x2 )
2
1
2
3. If a1 > a2 and b1 > b2
3. Eğer a1  a2 ve b1  b2 
b2,)b )
FX1 , X 2F( a1 , b(1a) ,≥b F) X1 , F
X 2 ( a2 (,a
X ,X
1 1
X ,X
2
2
1
2
1
2
⇒ monotonically
non-decreasing
monotonik olarak
azalmayanfunction
fonksiyon
15
Ortak kdf’nin özellikleri (devam)
4.
lim F X 1 X 2 ( x1 , x2 ) = F X
x1 → a +
X
(a, x 2 ),
lim+ FX X1, XX2 ((x11 , x22 )) 
=F
FXX 1,XX 2 ((x11, b)),
1
2
1
2
x →b
Sağdan sürekli
Üstten sürekli
x22 b
Pr[aa11 <
 XX1 1≤b1b, 1a,2a2 X<2 
(bX1 , ,bX2 ) ( bF1X, b, X2 )(a−1 , F
b2X) , X ( a1 , b2 )
 bF2 X] =, X F
5. Pr
Xb22 ≤
1
2
1
2
 FX , X (b1 , a2 )  FX , X (a1 , a2 )
1
2
1
x2
(a1,b2)
1
− FX1 , X 2 ( b1 , a2 ) + FX 1, X 2 ( a1 , a2 )
2
1
(b1,b2)
b2
a2
(a1,a2)
a1
(b1,a2)
b1
2
x1
2
16
Örnek:
x22b 22 4ac
0.5,
1≤
0.5,
0 0 x≤1 0
x1,
0x11,
x201,
≤0
2x2b<
⎧0.5,
f XffXX1X, X1 ,2xX(12x,(1,xx122,)x=2 )⎨ 
1 2
0, 0, otherwise
diğer diğer
2a
⎩0,

Ortak kdf'yi bulun
(
)
Ortak kdf'yi bulun
Find the joint cdf.
FX1 , X 2 ( x1 , x2 )  Pr  X 1  x1 , X 2  x2   
x1
x2
f
( z , z )dz dz

 Pr
FXF,XX , X( x(1,xx1 ,2 x) 2=) Pr
 −∞f X, X f( Xz1,, Xz 2()zdz1 , 2zdz2 )1dz2dz1
[ X1 X≤ 1x1, Xx12, ≤X x2 2]=x2∫−∞
x
x
 x1 X1 ,xX2 2 1 1 2 2
1
12
2
1
x2
(iii)
(v)
(ii)
(iv)
2
(i)
(i)
Durum i
(i)
1
x1
x1 < 0 veya x2 < 0 veya x1, x2 < 0
FXX11,,XX22 (( x11 , xx22 )) = 00
2
1
1
2
2
17
Durum ii
0 ≤ x1 ≤ 1, 0 ≤ x2 ≤ 2
x x
1 1x1 1 x22
11
FFXX1 , X, X2 ( x(1x,1x2 ), x2 ) =  dz
dz22dzdz1 1= x1 x21 x2
0
0
1
2
22
22
∫
0 0
Durum iii 0 ≤ x1 ≤ 1, x2 > 2
x2
(iii)
(v)
(ii)
(iv)
2
x
1 1x1 1 22
FFX1X, X, 2X( x(1x, 1x,2 x) 2) =   dzdz
dz
1 x=1 x1
dz
2
1
2
0 0
1
2
2 2
∫∫
(i)
00
(i)
Durum iv x1 > 1, 0 ≤ x2 ≤ 2
1 x2
1 1 x2
1 1
F
(
)
FX1X, X1 ,2X(2x1 , xx21),x2 =  dzdz
2 dz
1 1 = x2 x2
2 dz
0
0
2 2 00
2 2
1
Durum v
∫
x1 > 1, x2 > 2
11 11 2 2
dz2 dz1  1
X , X ( x1 , x2 ) 
FF
X 1 , 1X 2 2( x1 , x 2 ) = 2 0 0 dz2 dz1 = 1
2
∫∫
00
(i)
1
x1
18
Rastgele değişkenlerin bağımsızlığı
X1 , X2 gibi iki rastgele değişken aşağıdaki özellik sağlanırsa bağımsızdır denir
ffXX1 ,,XX2 ((xx11,,xx22))= ff XX1 ((xx11))f fX 2X ( x(2x),2 )
1
2
1
2
 x1 , x2
for all x1 , x2
or
veya
= F(Xx ()xF1) F(Xx (),x2 )  x , x
X ,(
X x (,xx1 , )x2) F
FXF
,
X
1
2
X1
1
X2
2
1
2
1
2
for all x1 , x2
1
2
1
2
19
Örnek:
−xx1 e−2
2 xx 2 ,
⎧
6e
∞
6e e , 00≤x1x1≤x2x

2 <
ff XX 1X, X2 ((xx11,, xx22 )) =
 ⎨
otherwise
diğer
⎩0, 0,
∞
0 ≤ x x12<x ∞
ffXX 1((xx11))= 6  e e dx2 23e 3 x , 0  x1  
1
1
2
1
2
2
1
(
1
)
f X 2 ( x2 ) = 6x∫ e − x1 e −2 x2 dx = 6e −2 x2 1 − e − x2 , 0 ≤ x2 < ∞
1
0  x 2 x
f X ( x1 )  6  e e dx1 6e 2 x (1  e  x ), 0  x2  
x1
2
1
2
2
1
0
(a) X1, X2 bağımsız mı?
fX 1 X 2 ( x1 , x2 ) = f X 1 ( x1 ) f X 2 ( x2 )
?
(
−3 x −2 x
−x
−xx1 e
2−2
x x2
6e
6e e
≠1818e
e3 x e12ex (121e− xe) 2
1
2
1
2
2
⇒bağımzsız değil
2
20
Örnek:
 bx2
 ( ax1  bx2 )
1
11−ee ax−ax
x1x ≥0,0,xx2 ≥00
1 e −bx2 e − ( ax1 +bx2, )
−
e
+
e
1
2
F
FXX11,,XX22 ((xx11, ,xx22) )=⎨
0,0
diğer

otherwise
(a) Marjinal kdf’leri bulun
 ax1 −ax
FXF1 X( x1()x
F
(
x
,

)

1

e
,e 1x1  0 x1 ≥ 0
=
F
x
,
∞
=
1
−
)
)
X1 , XX
1( 1
2
1
X
1
1 2
 bx2
FFX 2 ( x(2x) ) F
(

,
x
)

1

e
,−bx2 x2  0x ≥ 0
X
,
X
2
=
F
∞,
x
=
1
−
e
(
)
1
2
X2
2
X1 X 2
2
2
(b) Marginal oyf’leri (a) şıkkından bulun
x
dFdF
X1 (Xx11 () 1 )
 ax1 −ax1
=
=
ae , x1 x01 ≥ 0
f X1f(Xx1 1()x

ae
)
1
dx1dx1
dFdF
X 2 (Xx2 2()x2 )
 bx
f Xf1 X(2x1( )x2) =
 be
, 2 x2 x02 ≥ 0
= be2 −bx
dx2dx2
21
Örnek:
(devam)
(c) X1, X2 bağımsız mı?
kdf’leri kullanın
?
FFXX1 X,2X ((xx11,,xx22)) = FX 1 ((xx11) F
) FX X(2x(2 x) 2 )
1
2
1
(
2
)(
)
 ax1 − ax
 bx2 −bx
1
1−( bx
ax21 +bx
2 )(1  e
1 e
1 1 −
eeax−ax
1 e−bxe2−bx2 e+ ( ax

)(1

e
= 1− e
1 −)e 2
Evet, bağımsız...
)
Yes, they are independent
(d) Bağımsızlığı oyf’leri kullanarak gösterin
∂F
FX1X,1XX22((xx1 ,1 x2 ))
bx22
ffXX1 ,1XX22 ((xx11,,xx22) )=

,
= abe −axax11ee−bx
∂x
x11∂x
x22
x1x1≥0,0,x2x 2≥00
??
ffXX1 , XX 2 ((xx11,,xx22))=f fXX1 ( x(1x)1 f)Xf2 X( x2( )x2 )
1 2
1
2
−ax
ax1  −bx
bx2
 ax1
 bx
1
2  ae −ax
1
abe
e
be
abe e
= ae be −bx2 2
Evet,
bağımsız...
Yes, they
are independent
22
Şartlı oyf
Verilen X1 ve X2 gibi iki rastgele değişken için şu şartlı
yoğunluklar yazılabilir:
f Xf1 XX 2| X( x(1 x1x2x)2 )=
1
f Xf1X, X, X2 ( x(1x,1 x, x2 2))
1
2
f Xf 2X ( x( 2x)2 )
2
2
f X1f,XX ,2X( x(1 ,x1x,2x)2 )
f X 2fXX12 |(Xx1 2( xx21 )x1) =
1
2
f Xf1 X( x(1 x)1 )
1
Note that:
∞
Burada
∫ f

−∞

X 1| X 2
(x
1
x2 ) dx1 = 1 while

f X1 X 2 ( x1 x2 )dx1  1,


∞
∫
−∞
f X1| X 2 ( x1 x2 ) dx2 = ???
f X1 X 2 ( x1 x2 )dx2  ???
23
Şartlı oyf’nin ortak oyf’den bir dilim olarak yorumu:
fX1X 2 ( x1, x2 )
Kesit
x 20
f X1 X 2 ( x1 x20 ) 
2
fX1 X2 x1 x02 =
xx020
x2
X1
x1
XX
f X1 X 2 ( x1 , x20 )
( f
X
(x )
fX2
12 2
2
0
( x20 )
24
Örnek:
− x1 −2 x2
 x1e 2 x2,
⎧6e
00 ≤ xx1 ≤ xx2 < ∞
6
e
e
,

1
2
ff X 1X 2 ((xx1 ,,xx2 ))=⎨
0,
X1 , X 2
1
2
otherwise
⎩
0,
diğer
∞

ff XX11
−3 x
((xx1 )) = 66∫ ee−xx ee−22 xx dx
=
3e

dx 2 3e 3 x , ,
1

1
1
1
2
2
1
2
0 ≤ x1 < ∞
0  x1  
x1
x1
x2
x2
− x −2 x
−2 x
−x
 x e 2 x x
2 x (1 − e x ),
(
x
)
=
6
e
=
6e
f X ( x21 )  6∫ e e dx11 6e (1  e ),
X2
1

1
1
2
2
2
2
2
2
00 ≤ xx2 <∞
2
0
Şartlı oyf’leri bulun
2 x2− x −2 x
x
− x1
f X1 , X f2 ( x1 , x(2x) , x ) 6e x1 e6e
1
2 e 1
e
e
X
X
1
2
1 2
f Xf1 X 2 ( x1( xx2 |) x ) =
 =2 x2

, 0  x1 , 0x2≤ x ≤ x
 x2
 x=
2
X1| X 2
1
2
1
2
f X 2 ( xf 2 ) ( x ) 6e 6e
(1 −2ex2 (1)− e1−x2 e) 1 − e − x2
X2
2
 x1 2 x2
6
e
e − x1 −2 x2 x1 2 x2
f X 2 X1 ( x2 x1 |) x ) = f X 1 X 2 ( x1 ,x2 ) 6e
e 2e =
e 2e,2 x1 xe1−2x2x,2 x ≤ x < ∞
3 x1
f X 2 | X 1 ( x2 1 f X1 ( x1 )
1
2
3=e
−3 x1
f X1 , X 2 ( x1 , x2 )
f (x )
3e
25
Yoğunluklar için Bayes kuralı
X1 ve X2 gibi iki rd için şu yazılabilir:
f X 2| X 1 (f xX 2 X| x(1x) 2f Xx11()xf1)X ( x1 )
1
f X 1 | X 2 (fx1 | x(2 )x =x )  2 1
1 2
X1 X 2
f X 2 ( xf2) ( x )
X2
Now since:
(x ) =
f X 2 ( x2 ) 
f X2

2 
2

f∞X1 X 2 ( x1 , x2 )dx1 
∫f
X1 X 2
( x1 , x2 )dx1
=
∞

f X 2 X1 ( x2 x1 ) f X1 ( x1 )dx1
∫f
−∞
−∞
olduğundan
we have:
X 2 | X1
( x2 | x1 ) f X 1 ( x1 )dx1
f X 2| X 1 ( x2f X|2 xX11)(fxX21 (xx11) f X1 ( x1 )
f X 1 | X 2 ( xf1 X| xX2 )(=
x1 ∞x2 )  
1 2
f X1 ( x1 )dx1
∫ f X 2 | X1 ( xf2 X| xX1 )(fxX21 (xx11))dx
−∞


2
1
1
26
Örnek:
Şartlı oyf ve marjinal oyf’ler biliniyorsa:
e  x1 e − x1
f x1 (fxX11 (xx21)| x2 ) = x2 , − x20, 0x≤1 x1 x≤2 x2
1 e 1− e
 ∞
 x1− x12 −2
x2 x2
 x1−3 x1 ,
=
3e
f x1f(Xx1 1()x1) =6 6e∫ e e e dxdx
, 0 0≤x1x1<∞
2 3e
2 
x1 x1
(
x2 x2
)
 x−1x1 2−2
x2x2
2−2
x2x2
 −x2x2
f
(
x
)
=
6
e
e
x
=
6e
1
−
e
∞
f x2X(2x2 )2  6  ∫e e dx1 1 6e (1  e ),, 0 0≤x2x<2 
0
Bayes kuralını kullanarak ters şartlı oyf yi bulun:
f X X f(Xx1| Xx22() xf1X | (xx22 )) f X 2 ( x2 )
f Xf XX2 | X(1x(2 xx21 )| x1 ) =
f X ( x1 )f X 1 ( x1 )
1
2
2
2
1
1
)
(
2 xx2
 x2 x
−xx11 −2
2(1  e −
6
e
e
)2
e
2 x1 2 x2
1
−
e
6e


2
e
= 2ee2 x1 e,−2 x2 x, 1 x1x≤2 x 
= 3e−33xx11 (1  e −x2x)2
2 <∞
3e
(1 − e
)
27
İki rastgele değişkenin 1. ve 2. Momentleri
ortalama
m2
∫
mi i E  X i   
−∞
variance



x fXX1XX 2 ( x1 , 1x2 )dx
dx ,
21 21
 i i
1
2
2
 i2  Var  X i   E  X i  m2i   ,
Var [ X ] = E ( X − m )

i2  1, 2
1, 2
ii=1,
2
ilinti
]
(


)
rij  E  X=i Xfj   i,
i xdx
j f X idx
X j ( xi , x j )dxi dx j ,
 xj, =xx1,2
j
 i 
j
i
j
i, j  1, 2
covariance
Cov  X
m   X  m  j,) i, ji, j1,=21, 2
ccijij =Cov
Xii,,XXj j =EE X( X
i 
i −i mi )( jX j −j m
28
İlinti/Kovaryans Bağıntıları
−im
ccij ij=rijr
mijm j
ij m
Cov  X
X i ,, XXj ⎤=EE X iXX jX ⎤E− X
 E ⋅XEj  X
i X
Cov
E
[
i
i
j⎦
j⎦
i]
j
Cov[Xi,Xj] = 0 olmasi durumunda then Xi ve Xj ilintisizdir denir.
Bu durumda
E [ X1 X 2 ] = E [ X1 ] E [ X 2 ]
olur.
(E[XiXj] = 0 olması durumunda rastgele değişkenler ortogonal dir denir.)
29
İki rastgele değişken için diğer bağıntılar
Bağımsız rastgele değişkenler ilintisizdir:
Proof:
İspat
∞
E [ X1 X 2 ] = ∫
∫

∞
x x f X 1X 2 ( x1 , x2 ) dx1dx2
1 2
 
−∞ −∞
E  X 1 X 2  ∞  ∞  x1 x2 f X1 X 2 ( x1 x2 )dx1dx2
=∫
 
∫

xx f
 
−∞ −∞ 1 2 X 1
 
 
∞
( x1 ) f X ( x2 ) dx1dx2
2
x1 x2 f X1 ( x1 ) f X 2 ( x2 ) dx1dx2
( since X 1 , X 2 are independent )
∞
(bağımsızlıktan dolayı)
E [ X 1 X 2 ] = ∫ x1 f X 1 ( x1 ) dx1 ∫ x2 f X2 ( x2 ) dx2 = E [ X 1 ] E [ X 2 ]
E  X 1 X 2  −  x1 f X1 ( x1 )dx1−∞
 x2 f X 2 ( x2 )dx2  E  X1  E  X 2 


 X 1 ve X 2 ilintisizdir
vice versa is not
true (except for
Gaussian
random
variables)
tersi doğru değildir (Gausyen
rastgele değişkenler hariç)
30
İlinti Bağıntılarının Özeti
• Cov [X1, X2] =0 ⇒ X1 ve X2 ilintisizdir
• E [X1X2] =0 ⇒ X1 ve X2 ortogonaldir
• X1 ve X2 nin ilinti katsayısı şu şekilde tanımlanır

E  X 1  m1  X 2  m2  
X X
1
2

Cov  X 1 , X 2 
X X
1
2
1    1