Rasgele değişkenlerin dönüşümleri File

1
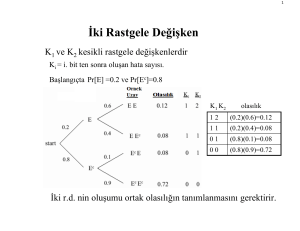
Rastgele Değişkenin Dönüşümleri
Y = g(X) verildiğinde X rastgele ise Y de rastgeledir.
• Amaç fX(x) verildiğinde fY(y) yi bulmaktır.
g (⋅)
X
Y
Y = g (X) and X = g−1 (Y)
• Sistem hafızasızdır:
Y, sadece X in şu andaki değerlerine
bağlıdır.
Y = 2X )
─ Giriş-çıkış ilişkisi lineer ya da nonlineer olabilir.
─ X = g– 1(Y) nin tersi çok değerli (multi-valued) olabilir.
(örnek:
2
Tek Değerli Durum
Transfer Karakteristiği
dy
Y=g(X)
y
dx
0
x
Pr [ y < Y ≤ y + dy ] = Pr [ x < X ≤ x + dx ]
fY ( y ) dy = f X ( x ) dx
fY ( y ) =
1
fX ( x)
dy dx
x = g −1 ( y )
3
Örnek:
Y = g(X) = 2X, ve X in oyf si aşağıdaki gibi olsun
 1⎧ 1
 ⎪, 0 0X≤ X4 ≤ 4
ffX ( (x)x) =
 4⎨ 4
X

 0, 0 diğer
otherwise.
f X (x )
1/4
0
burada
−1
dy
1
= 2, X = g (Y ) = Y olur.
dx
2
44
xx
44
xx
8
y
Y nin oyf si şu şekilde elde edilir:
fY ( y ) =
1
fX ( x)
dy dx
x = g −1 ( y )
⎧11
⎪ , 00≤ YY ≤
 88
=⎨88

diğer
00, otherwise.
0
fY ( y )
1/8
0
88 y y
4
y
Grafik Gösterim:
Y Y =
aXaX
8
y
11 f x  ⎛y y ⎞
f
(
x
)

X
f Y ( y ) = | a | f X ⎪a  ⎪
a
a
8
0
1/8
fY(y)
⎝ ⎠
0
4
f X (x )
1/4
0
x
4
x
5
Örnek:
Y = g(X) = X+3, ve X in oyf si aşağıdaki gibi olsun
f X (x )
 1⎧ 1
 ⎪ , 00≤XX ≤4 4
f fX ( x( )x 
) = 4⎨ 4
X

diğer
 0,0 otherwise.
1/4
0
Burada
−1
dy
= 1, X = g (Y ) = Y − 3 olur.
dx
Y nin oyf si şu şekilde elde edilir:
fY ( Yy ) 
1
f X ( x)X
| dy dy
dx |dx
1
 ,1 3  Y  7
  4⎧
3≤Y ≤ 7
⎪
=
 0,⎨ 4 diğer
0 otherwise.
x  g 1 ( y )
x= g
x
4
x
y
7
3
0
−1
4
( y)
fY( y )
1/4
0
33
77
yy
6
7
y
Grafik Gösterim:
y
3
3
0
1/4
fY(y)
7
0
4
f X (x )
1/4
0
x
4
x
7
Genelleme:
Y = g(X) = aX + b, ve girişin oyf si fX(x) verildiğinde fY(y) bulma
işlemi.
Burada
We
have
dydy
Y b b
| =
a |,aX, X
 g=1 g
(Y−1) (Y ) = Y −olur.
.
dxdx
a a
dy
Y = g(X) = aX+b
y
Transfer Karakteristiği
b
−b
0
dx
x
a
ffYY((yy) )=
11
1
 y b 
f Xf(Xx() x ) y b  = 1f XfX ⎪⎛ y −b ⎪⎞
x
dydydxdx
| a |a  ⎝ a a  ⎠
a y −b
x=
a
8
Önemli Dönüşüm
Y  aX  b
Y = aX + b
1
 −y b ⎞b 
y
1
⎛
f
(
y
)

f
fY Y( y ) = | a f|X ⎪X  a ⎪ 
a
⎝ a ⎠
Özel Durumlar
aX
Y Y =aX
1
 y
fY ( y ) 
fX  
| 1a | ⎛ ay ⎞
fY ( y ) =
fX ⎪ ⎪
a
⎝ a⎠
YY=XX+ b b
fY ( y )  f X ( y  b )
fY ( y ) = f X ( y − b )
9
Örnek:
fX(x) Gausyen bir oyf olsun:
2
( x −m ) 2
− ( x  m2XX )

22σ
 X2
11
ff x ((xx)) =
ee
X
22π
σX
−∞<xx<∞
X
x
buradan
) aX ) mX 
( ( y−b( y) ab−m
− 
2
11 1 1
ee
fYy (( y )) =
σX x
|aa | 2π2
2σ 2X2 X2
2
( y −( b+amX y) )( b  amX ) 
−
2 2
1 1
= 
e 2 a eσ X
2π 2
aσ X| a |  X
2
2
2 a 2 X2
Yani, fY(y) mY = b + amX, Y = |a|X olan bir Gausyen yoğunluktur.
10
Alternatif Metod: Kümülatif Dağılım Fonksiyonu Kullanımı
Örnek:
Y = aX + b
a>0
FFYY(y)
( y ) den:
 Pr[Y  y ]  Pr[aX  b  y ]
 [Y ≤ yy ]=bPr
 [ aX +by≤yb] 
FY ( 
y )Pr
= Pr
X
F

 ⎡
= Pr X ≤
ay − b ⎤
a
X
= FX
 a 
⎡ y − b ⎤
Y = aX +b
y
b
a
x
= (y −b)/a
Buradan
y −b
1
y −b
d
d
FXy ⎪⎛ b  ⎪⎞ =1 f X⎪⎛y  b ⎪⎞
FY ( y )d=
FYdy
( y) 
Fdy
⎠ af X ⎝ a ⎠
X  ⎝ a 
fY (dy ) =
fY ( y ) 
dy
dy
 a 
a
 a 
11
Örnek:
Yukarıdaki problemi a < 0 için tekrarlayalım
y − by⎤ b
X > X  ⎪ 
FYF(Y y()y=) 
PrPr[
[Y Y≤ y] =y ]Pr⎡⎪Pr
⎣  a ⎦a 
⎡  y − by ⎤ b 
⎡ y − b ⎤y  b 
= 1−1Pr
 PrX≤X a = 1−F1X  FXa 
a
a 



bb
y

x
=(y −b)/a
Buradan
d
d ⎡
1 ⎛ y −b⎞
⎛ y − b ⎞⎤
fY ( y ) = d FY ( y ) = d⎪1− FX ⎪  y ⎪⎪ b= − f X ⎪1
⎪ y  b 
fY ( y )  dy FY ( y ) dy ⎣ 1  F⎝ X a ⎠ ⎦  a  ⎝ faX ⎠

dy
dy 
 a 
a
 a 
12
Rastgele Değişkenin Fonksiyonu
Çok Dğerli Durum
Transfer Karakteristiği
dy
y
Y=g (X)
dx1
dx3
dx2
x1
x2
x3
Pr [ y < Y ≤ y + dy ] = Pr [ x1 < X ≤ x1 + dx1 ] + Pr [ x2 < X ≤ x2 + dx2 ]
+... + Pr [ xm < X ≤ xm + dxm ]
fY ( y ) dy = f X ( x ) dx1
x = x1
+ f X ( x ) dx2
x = x2
m
m
+ ... + f X ( x ) dxm
1
ffY (( yy)) = ∑ 1 f f(Xx)( x ) x = g −1 y

Y
x  g ( yk) ( )
dy dx X
kk=1
1 dy dx
1
k
x = xm
13
y
Örnek:
Y = g ( X ) = aX 2
a > 0, − ∞ < X < ∞
dy
Y=g (X)
dxdx
x1
x2
X rastgele değişkeninin oyf si biliniyor. fY(y) yi bulun.
1
1
1
+f X ( x1) x  g 1f(Xy )( x )
fY ( y ) fY ( y ) = f X ( x) x  gfX1 ((y )x)
dy dx dy dx 1
dy −1dx dy dx 2
x = g1
( y)
y
y
1
y x1  g 2 ( y )  −1
x1  g ( y )  −1

x1 = g1 ( ya) = −
x2 = g 2 (ay ) = +
a
dy
 2dy
ax  2 ay
dx
= 2ax = 2 ay
1
1
dx
1  
fY ( y ) 
 f X 1 
fY2( yay
) = 
2 ay
y
⎡  ⎛ f X
⎪af  −
X
⎪
⎝

y 
y⎞   ⎛ y y ⎞0⎤
 +a fX +
⎪
⎪
⎪⎪
a⎠
⎝
a⎠
x = g 2−1 ( y )
y
a
y>0
14
Örnek: