iki zamanlı benzinli bir motorun performansının bilgisayar yardımı ile

İKİ ZAMANLI BENZİNLİ BİR MOTORUN PERFORMANSININ
BİLGİSAYAR SİMÜLASYONU YARDIMI İLE ANALİZİ
GÖKSEL KAYA
YÜKSEK LİSANS TEZİ
MAKİNE EĞİTİMİ
GAZİ ÜNİVERSİTESİ
FEN BİLİMLERİ ENSTİTÜSÜ
HAZİRAN 2010
ANKARA
Göksel KAYA tarafından hazırlanan İKİ ZAMANLI BENZİNLİ BİR MOTORUN
PERFORMANSININ BİLGİSAYAR SİMÜLASYONU YARDIMI İLE ANALİZİ
adlı bu tezin Yüksek Lisans tezi olarak uygun olduğunu onaylarım.
Prof. Dr. Selim ÇETİNKAYA
Tez Danışmanı, Makine Eğitimi Anabilim Dalı
Bu çalışma, jürimiz tarafından oy birliği ile Makine Eğitimi Anabilim Dalında
Yüksek Lisans olarak kabul edilmiştir.
Prof. Dr. Selim ÇETİNKAYA
Makine Eğitimi Ana Bilim Dalı, Gazi Üniversitesi
Prof. Dr. A. İhsan ACAR
Tarımsal Makinaları Ana Bilim Dalı, Ankara Üniversitesi
Prof. Dr. H. Serdar YÜCESU
Makine Eğitimi Ana Bilim Dalı, Gazi Üniversitesi
Prof. Dr. Halit KARABULUT
Makine Eğitimi Ana Bilim Dalı, Gazi Üniversitesi
Doç. Dr. Can ÇINAR
Makine Eğitimi Ana Bilim Dalı, Gazi Üniversitesi
Tarih:
29/06/2010
Bu tez ile G.Ü. Fen Bilimleri Enstitüsü Yönetim Kurulu Yüksek Lisans derecesini
onamıştır.
Prof. Dr. Bilal TOKLU
Fen Bilimleri Enstitüsü Müdürü
TEZ BİLDİRİMİ
Tez içindeki bütün bilgilerin etik davranış ve akademik kurallar çerçevesinde elde
edilerek sunulduğunu, ayrıca tez yazım kurallarına uygun olarak hazırlanan bu
çalışmada bana ait olmayan her türlü ifade ve bilginin kaynağına eksiksiz atıf
yapıldığını bildiririm.
Göksel KAYA
iv
İKİ ZAMANLI BENZİNLİ BİR MOTORUN PERFORMANSININ
BİLGİSAYAR SİMÜLASYONU YARDIMI İLE ANALİZİ
(Yüksek Lisans Tezi)
Göksel KAYA
GAZİ ÜNİVERSİTESİ
FEN BİLİMLERİ ENSTİTÜSÜ
Haziran 2010
ÖZET
İçten yanmalı motorların ekonomik ve etkili kullanımı giderek daha çok önem
kazanmaktadır. Bu nedenle, motor performansının iyileştirilmesi konusunda
yoğun
çalışmalar
yapılmaktadır.
Motor
performansının
belirlenmesi,
matematiksel model kullanımı ve deneysel çalışma olmak üzere iki aşamada
yapılmaktadır. Birinci aşamada, henüz tasarı halindeki motorun performansı
çevrim
analizi
aracılığı
ile
teorik
matematiksel
model
kullanılarak
belirlenmekte, motor parametrelerinden her birinin motor karakteristiklerine
etkileri incelenmektedir. İkinci aşamada, teorik çalışma doğrultusunda deneysel
çalışmalar yapılmaktadır. Bilgisayar teknolojisindeki baş döndürücü gelişmeler
nedeniyle
mühendislikte
oluşturulan
matematiksel
modellerin
çözümü
kolaylaşmış, teorik çalışmalar daha da önem kazanmıştır. Simülasyonlar
sonucunda içten yanmalı motorların silindir basınç ve sıcaklığı, ortalama indike
basınç, ortalama efektif basınç ve ısıl verim gibi karakteristik değerleri
hesaplanabilmektedir. Ancak, sonuçların geçerliliği, değişik işletme koşullarının
ve bunlara uygun performansı belirleyecek parametrelerin matematiksel
modele gerçekçi bir yaklaşımla katılmasına bağlıdır. Bu çalışmada, iki zamanlı
benzinli bir motorun performansının analizi için MATLAB/SIMULINK
programlama dilinin kullanılmasıyla bir bilgisayar programı geliştirilmiştir.
v
Simülasyon sonucunda silindir basınç ve sıcaklığı, ortalama indike ve efektif
basınç, efektif güç, efektif moment ve ısıl verim gibi karakteristik değerler
hesaplanmıştır ve motor hızı veya krank mili açısına bağlı olarak grafikleri
çizdirilmiştir. Sonuçlar test sonuçlarıyla uyuşmaktadır.
Bilim Kodu
: 708.3.026
Anahtar Kelimeler : Benzinli motor, simülasyon, modelleme, iki zamanlı
motor, motor performansı
Sayfa Adedi
: 106
Tez Yöneticisi
: Prof. Dr. Selim ÇETİNKAYA
vi
PERFORMANCE ANALYSIS OF A TWO-STROKE SPARK IGNITION
ENGINE BY COMPUTER SIMULATION
(M.Sc. Thesis)
Göksel KAYA
GAZİ UNIVERSITY
INSTITUTE OF SCIENCE AND TECHNOLOGY
June 2010
ABSTRACT
Economic and effective use of internal combustion engines is becoming more
and more important. Therefore, intense studies about increasing the
performance of the engines are performed. Determination of the engine
performance has been done in two stages. At the first stage, the performance
of the engine still in a draft form is determined through the cycle analysis in
a theoretical way by using a mathematical model. At this stage each
parameter of the engine is changed and its effect on engine characteristics
are determined. At the second stage, experimental studies are done in
accordance with theoretical work. Due to the enormous advances in
computer technology, the solutions of the mathematical models formed in
engineering have become easier and theoretical work has gained greater
importance.
Characteristic
values
such
as
cylinder
pressure
and
temperature, mean indicated pressure, mean effective pressure and thermal
efficiency can be calculated by using the generated simulation programs.
However, the validity of the results depends on attending of the different
operating conditions and the parameters which will determine the
appropriate performance into a mathematical model in a realistic approach.
In this study, a computer program was developed to simulate the
vii
performance
of
a
two-stroke
spark
ignition
engine
by
using
MATLAB/SIMULINK programming language.
Characteristic values such as cylinder pressure and temperature, mean
indicated and effective pressure, effective power, effective torque and
thermal efficiency were calculated and their graphics were drawn depending
on the engine speed and the angle of crankshaft by using the generated
simulation program. Results are compatible with the test results.
Science Code
Key Words
Page Number
Adviser
: 708.3.026
: Spark ignition engine, simulation, modeling, two-stroke
engine, engine performance
: 106
: Prof. Dr. Selim ÇETİNKAYA
viii
TEŞEKKÜR
Çalışmalarım boyunca değerli yardım ve katkılarıyla beni yönlendiren Hocam Prof.
Dr. Selim ÇETİNKAYA’ya, ayrıca çalışma arkadaşlarım İdris SANCAKTAR,
Ergün YÜCESOY, Özer ŞENYURT ve M. Selim ÇAKIROĞLU’na, manevi
destekleriyle beni hiçbir zaman yalnız bırakmayan çok değerli aileme teşekkürü bir
borç bilirim.
ix
İÇİNDEKİLER
Sayfa
ÖZET .......................................................................................................................... iv
ABSTRACT ................................................................................................................ vi
TEŞEKKÜR .............................................................................................................. viii
İÇİNDEKİLER ........................................................................................................... ix
ÇİZELGELERİN LİSTESİ ........................................................................................ xii
ŞEKİLLERİN LİSTESİ ............................................................................................ xiii
SİMGELER VE KISALTMALAR ........................................................................... xvi
1. GİRİŞ ..................................................................................................................... 1
2. LİTERATÜR ÖZETİ ............................................................................................. 3
3. İKİ ZAMANLI MOTORLAR ............................................................................. 14
3.1. Çalışma Prensipleri ...................................................................................... 14
3.1.1. Sıkıştırma işlemi ................................................................................ 15
3.1.2. Yanma ve genişleme işlemi ............................................................... 15
3.2. Port Zaman Diyagramları............................................................................. 17
3.3. İki ve Dört Zamanlı Motorların Kıyaslanması ............................................. 17
3.4. Süpürme Teorisi ........................................................................................... 19
3.4.1. Dönüş (ters) akışlı süpürme ............................................................... 19
4. TEORİK ÇEVRİM ANALİZİ ............................................................................. 21
4.1. İki Zamanlı Motorların Hava Standart Otto Çevrimi................................... 21
4.2. Çevrimin İncelenmesi .................................................................................. 25
4.2.1. Sıkıştırma işlemi (a-c) ....................................................................... 25
x
Sayfa
4.2.2. Sabit hacimde yanma (c-Z) ............................................................... 25
4.2.3. Genişleme işlemi (z-b) ...................................................................... 26
5. GERÇEK ÇEVRİM HESAPLAMALARI İÇİN ANALİTİK MODEL .............. 27
5.1. Gerçek Motor Çevrimlerindeki Sınırlamalar ............................................... 27
5.2. Krank Mili Açısına Göre Piston Pozisyonu ................................................. 29
5.3. Çevrim İşlemleri .......................................................................................... 31
5.3.1. Süpürme işlemi .................................................................................. 32
5.3.2. Sıkıştırma işlemi ................................................................................ 35
5.3.3. Yanma işlemi ..................................................................................... 36
5.3.4. Genişleme işlemi ............................................................................... 49
5.3.5. Egzoz işlemi ...................................................................................... 50
5.4. Motor Performans Karakteristikleri ............................................................. 51
5.4.1. Ortalama indike ve efektif basınçlar.................................................. 52
5.4.2. İndike ve efektif güçler ...................................................................... 54
5.4.3. İndike ve efektif momentler .............................................................. 54
5.4.4. İndike ve efektif ısıl verimler ............................................................ 55
5.4.5. İndike ve efektif özgül yakıt tüketimleri ........................................... 56
6. SİMÜLASYON SONUÇLARI VE TARTIŞMA ................................................ 59
6.1. Silindir Basınç, Sıcaklık ve Motor Karakteristik Eğrileri ............................ 60
6.2. Sıkıştırma Oranının Etkisi ............................................................................ 70
6.3. Hava Fazlalık Katsayısının Etkisi ................................................................ 75
7. SONUÇ VE ÖNERİLER ..................................................................................... 81
KAYNAKLAR .......................................................................................................... 83
xi
Sayfa
EKLER ....................................................................................................................... 86
EK-1 Simülasyon Program Kodları ........................................................................... 87
ÖZGEÇMİŞ ............................................................................................................... 96
xii
ÇİZELGELERİN LİSTESİ
Çizelge
Sayfa
Çizelge 5.1. Bazı gazların lineer özgül ısı değişimindeki A ve B katsayıları ........... 46
Çizelge 5.2. Mekanik kayıplar ortalama basıncındaki a ve b katsayıları .................. 53
Çizelge 6.1. Simülasyonu yapılan motorun karakteristikleri ..................................... 59
Çizelge 6.2. Simülasyonu yapılan motorun çevrim hesabındaki bazı kabuller ......... 60
Çizelge 6.3. Motor özellikleri ................................................................................... 64
Çizelge 6.4. Motor özellikleri ................................................................................... 66
xiii
ŞEKİLLERİN LİSTESİ
Şekil
Sayfa
Şekil 2.1. Clerk tarafından yapılan iki zamanlı motorun şeması ................................. 4
Şekil 2.2. Simülasyon sonuçlarına göre yanma hacmi ve yüzeyi ................................ 6
Şekil 2.3. İki zamanlı bir motorun sayısal çözüm ağı .................................................. 9
Şekil 2.4. Silindir basıncı-piston hareketi diyagramı ................................................... 9
Şekil 2.5. Gaz sıcaklığı-zaman diyagramı.................................................................. 10
Şekil 2.6. Hava fazlalık katsayısının silindir basıncına etkisi .................................... 11
Şekil 2.7. Hava fazlalık katsayısının gaz sıcaklığına etkisi ....................................... 11
Şekil 2.8. Krank mili açısı-silindir basıncı diyagramı................................................ 12
Şekil 3.1. İki zamanlı bir motorun gaz değişim diyagramı ........................................ 14
Şekil 3.2. İki zamanlı benzinli bir motorun çalışmasının şematik gösterimi ............. 14
Şekil 3.3. İki zamanlı benzinli bir motorun port zamanlama diyagramı .................... 17
Şekil 3.4. Dönüş (ters) akımlı süpürme...................................................................... 20
Şekil 4.1. Hava standart otto çevrimi ......................................................................... 23
Şekil 5.1. İçten yanmalı motorlar için piston-krank-biyel geometrisi ....................... 30
Şekil 5.2. İki zamanlı bir motorda gerçek basınç-hacim diyagramı .......................... 31
Şekil 6.1. Silindir basıncının silindir hacmiyle değişimi ........................................... 61
Şekil 6.2. Silindir basıncının krank mili açısıyla değişimi ........................................ 61
Şekil 6.3. Gaz sıcaklığının krank mili açısıyla değişimi ............................................ 62
Şekil 6.4. Ortalama indike ve efektif basıncın motor hızına bağlı değişimi .............. 62
Şekil 6.5. Ortalama indike ve efektif momentin motor hızına bağlı değişimi ........... 63
Şekil 6.6. Ortalama indike ve efektif gücün motor hızına bağlı değişimi.................. 63
xiv
Şekil
Sayfa
Şekil 6.7. Motor gücü ve momentinin motor hızına bağlı değişimi ......................... 65
Şekil 6.8. Motor gücü ve momentinin motor hızına bağlı değişimi .......................... 65
Şekil 6.9. Motor gücü-motor hızı grafiği ................................................................... 66
Şekil 6.10. Motor gücünün motor hızına bağlı değişimi............................................ 67
Şekil 6.11. Motor momenti-motor hızı grafiği ........................................................... 67
Şekil 6.12. Motor momentinin motor hızına bağlı değişimi ...................................... 68
Şekil 6.13. Ortalama indike ve efektif özgül yakıt tüketiminin motor hızına bağlı ... 69
Şekil 6.14. Ortalama indike ve efektif verimin motor hızına bağlı değişimi ............. 70
Şekil 6.15. Sıkıştırma oranının silindir basıncına etkisi............................................. 71
Şekil 6.16. Sıkıştırma oranının silindir basıncına etkisi............................................. 71
Şekil 6.17. Sıkıştırma oranının gaz sıcaklığına etkisi ................................................ 72
Şekil 6.18. Sıkıştırma oranının ortalama efektif basınca etkisi .................................. 72
Şekil 6.19. Sıkıştırma oranının efektif momente etkisi .............................................. 73
Şekil 6.20. Sıkıştırma oranının efektif güce etkisi ..................................................... 73
Şekil 6.21. Sıkıştırma oranının efektif özgül yakıt tüketimine etkisi......................... 74
Şekil 6.22. Sıkıştırma oranının efektif verime etkisi.................................................. 75
Şekil 6.23. Hava fazlalık katsayısının silindir basıncına etkisi .................................. 76
Şekil 6.24. Hava fazlalık katsayısının silindir basıncına etkisi .................................. 76
Şekil 6.25. Hava fazlalık katsayısının gaz sıcaklığına etkisi ..................................... 77
Şekil 6.26. Hava fazlalık katsayısının ortalama efektif basınca etkisi ....................... 77
Şekil 6.27. Hava fazlalık katsayısının efektif momente etkisi ................................... 78
Şekil 6.28. Hava fazlalık katsayısının efektif güce etkisi .......................................... 78
Şekil 6.29. Hava fazlalık katsayısının efektif özgül yakıt tüketimine etkisi .............. 79
xv
Şekil
Sayfa
Şekil 6.30. Hava fazlalık katsayısının efektif verime etkisi ....................................... 79
xvi
SİMGELER VE KISALTMALAR
Bu çalışmada kullanılmış bazı simgeler ve kısaltmalar, açıklamaları ile birlikte
aşağıda sunulmuştur.
Simgeler
Açıklama
ε
Sıkıştırma oranı
ρ
Yoğunluk (kg/m3)
γr
Artık gazlar katsayısı
φi
İndikatör diyagramı yuvarlatma katsayısı
ξz
Yanmada ısıdan yararlanma verimi
β
Kısılma kayıpları katsayısı
ζ
Sürtünme kayıpları katsayısı
λ
Basınç artma oranı
V
Nable operatörü
α
Hava fazlalık katsayısı
ω
Açısal hız (rad/s)
μ
Molekülsel değişim katsayısı
η
Verim (%)
ηe
Efektif verim (%)
ηi
İndike verim (%)
ηv
Hacimsel verim (%)
θ
Krank mili açısı ( )
s
Piston yolu (m)
Ue
Türbülans alev hızı (m/s)
l
Biyel boyu (m)
r
Krank yarıçapı (m)
cv
Sabit hacimde özgül ısı (kJ/kmol K)
ο
xvii
Simgeler
Açıklama
cp
Sabit basınçta özgül ısı (kJ/kmol K)
Apis
Piston alana (m2)
bi
İndike özgül yakıt tüketimi (kg/kWh)
be
Efektif özgül yakıt tüketimi (kg/kWh)
dpis
Piston çapı (m)
H
Strok (m)
Hu
Alt ısıl değer (kJ/kg)
k
Bir devirde iş yapan kurs sayısı
ka
Adyabatik üs
kWG
Su gazı denge katsayısı yerine geçen katsayı
Kwg
Su gazı denge katsayısı
m
Kütle (kg)
n
Devir (1/min)
np
Politropik üs
N
Mol sayısı (kmol)
Mi
İndike moment (Nm)
Me
Efektif moment (Nm)
P
Basınç (bar)
Patm
Atmosfer basıncı (bar)
Pr
Egzoz basıncı (bar)
Peg
Egzoz sisteminin geri basınç farkı (bar)
Pmi
Ortalama indike basınç (bar)
Pme
Ortalama efektif basınç (bar)
Pmm
Mekanik kayıplar ortalama basıncı (bar)
Pi
İndike güç (kW)
Pe
Efektif güç (kW)
R
Üniversal gaz sabiti (kJ/kg K)
Re
Reynold sayısı
S
Entropi (kJ/kgK)
xviii
Simgeler
Açıklama
T
Sıcaklık (K)
Tatm
Atmosfer sıcaklığı (K)
Tr
Egzoz sıcaklığı (K)
Q
Isı (kJ)
U
İç enerji (kJ)
V
Hacim (m3)
Vc
Yanma odası hacmi (m3)
Vh
Kurs hacmi (m3)
Vsv
Süpürme hacmi (m3)
Vp
Piston hızı (m/s)
Vm
En dar manifold kesitindeki hız (m/s)
W
İş (kJ)
z
Silindir sayısı
Kısaltmalar
Açıklama
AA
Ateşleme avansı
AÖN
Alt ölü nokta
EGAA
Egzoz portu açılma avansı
EGKG
Egzoz portu kapanma gecikmesi
EMAA
Emme portu açılma avansı
EMKG
Emme portu kapanma gecikmesi
HFK
Hava fazlalık katsayısı
1
1.
GİRİŞ
Teknolojideki gelişmelere paralel olarak içten yanmalı motorlardaki gelişmeler de
şaşırtıcı boyutlardadır. Ancak motorların temel yapılarında esaslı bir değişiklik
olmamıştır.
Yeni
geliştirilmesinde
bir
motor
motorun
tasarlanmasında
karakteristikleri
önemli
veya
bir
mevcut
yer
tutar.
motorun
Motor
karakteristiklerinin belirlenmesi, motor deneylerinin esasını teşkil eder ve sadece
motorun çıplak ve statik olarak performansının bilinmesini sağlamayıp aynı zamanda
taşıt üzerinde gerçek hizmet şartlarındaki performansı hakkında da önemli bilgiler
verir. Bu amaçla motorun termodinamik davranışının incelenmesi ve gerçek hizmet
şartlarındaki
performansının
belirlenmesi
için
simülasyon
programları
kullanılmaktadır.
Bilgisayarlarla, bir motorun çalışması sırasında gerçekleşen olayların sayısal
modellemesi yapılıp imalatçıların kullanımına sunulduğunda, uzun sürecek deneysel
işlemlerin süresi kısaltılmaktadır. Bilgisayarların teknolojide yerlerini alması ve
sayısal
hesaplama
yöntemlerindeki
iyileşmeler,
içten
yanmalı
motor
karakteristiklerinin belirlenmesi için yapılan hesaplamalardan daha gerçekçi sonuçlar
alınmasını sağlamıştır. Örneğin, iyi bir yakıt ekonomisine ve egzoz emisyonlarının
azaltılmasına yönelik taleplerin karşılanması için teorik model kullanımı iyi bir
araçtır. Motorların matematiksel olarak modellenmesi sayesinde;
1. Farklı çalışma koşullarında motorun beklenen davranışı gerçekleştirme yeteneği
belirlenebilmektedir [1].
2. Artan bilgisayar hızları ve kısalan analiz süreleri ile maliyet daha etkin olarak
çıkarılabilmekte ve uygulanan sayısal metotlarla simülasyonda iyileşme
sağlanmaktadır [1].
2
3. Motor parametrelerinin her biri için matematiksel modelin çözümlemesi ile
performans
değişimi
araştırılabilmekte,
optimum
motor
karakteristikleri
belirlenebilmektedir [1].
Motorların termodinamik davranışlarının incelenmesi 1950’li yıllarda ideal
çevrimlerle yapılmış, bilgisayar teknolojisinin gelişmesine paralel olarak 1960’lı
yılların başından itibaren daha gerçekçi ifadeler kullanılmaya başlanmıştır. 1980’li
yıllardan itibaren ise hem termodinamik hem de akış mekaniği ile ilgili
hesaplamalara dayalı çok boyutlu modeller kullanılmaya başlanmış ve daha gerçekçi
sonuçların elde edilmesi mümkün olmuştur.
Çok boyutlu modeller daha gerçekçi sonuçlar vermesine rağmen modellemenin
uygulanmasındaki zorluklar dezavantajıdır. Tek boyutlu modellerin ise üç boyutlu
modellere göre daha basit yapıları vardır ve termodinamiksel ve deneysel verilere
bağlı modellerde oldukça iyi sonuçlar vermektedir [2].
Benzinli
bir
motorun
simülasyonunu
sıkıştırma
ile
ateşlemeli
motorun
simülasyonundan ayıran temel farklar, yanma işlemi ile karışımın oluşturulmasında
toplanmaktadır. Benzinli bir motordaki yanmanın analizi için, yanma odası genellikle
iki bölgeye ayrılmaktadır. Bu bölgeler, alev cephesi tarafından birbirinden ayrılan,
yanmış ve yanmamış gazlardan oluşan bölgelerdir. Her iki bölgenin farklı
sıcaklıklarda ancak aynı basınçta oldukları kabul edilmektedir. İşte simülasyonlarda
karşılaşılan ve tam olarak çözülemeyen gerçek problem, motor geometrisi ile yanmış
gaz hacminin biçimi arasındaki ilişkidir. Seçilebilecek modellerden bir tanesi,
yanmış gazlar için basit geometrik biçimden oluşan bir ısı transfer yüzeyi ve
ortalama sıcaklıkları kullanmaktır [3].
Bu çalışmanın amacı, iki zamanlı benzinli bir motorun performansının bilgisayar
ortamında simülasyonla belirlenmesidir. Simülasyon programının hazırlanmasında
MATLAB/SIMULINK programlama dili kullanılmıştır. Bu programın tercih edilme
sebebi, mühendislik alanında geçerli ve yaygın bir kullanım alanının bulunuyor
olmasıdır.
3
2.
LİTERATÜR ÖZETİ
Çeşitli yakıtların bir silindir piston düzeneği içerisinde yanması sonunda elde edilen
ısı enerjisinden mekanik enerji elde etmek amacı ile 150 yıldan beri çeşitli ısı
makineleri yapılmaktadır. 1860’da Lenoir tarafından hava gazı ile çalışan verimi %
5’ten küçük olan bir gaz makinesi yapılmıştır. 1867’de Nicolaus August Otto
atmosferik gaz motorunu yapmıştır. Daha sonra Otto şimdikine benzer hava gazı ile
çalışan, alev ile ateşlemenin yapıldığı, hızı 200 1/min’den düşük 4 zamanlı motoru
yapmıştır. Bunun ardından Gottlieb Daimler, petrolden üretilen hafif yakıt kullanmış
ve 1883’te devir sayısını 800 1/min’e çıkarmıştır. Yine 1883’te Wilhelm Maybach
karbüratör aracılığı ile yakıt-hava karışımının hazırlandığı motoru yapmıştır. Karl
Benz sisteme elektrikli ateşleme donanımını ekleyerek 1885’te dört zamanlı bir
benzin motoru ile 3 tekerlekli bir taşıtı başarılı bir şekilde yürütmüştür. Bu arada bir
Alman mühendis Rudolf Diesel bir makalesinde sıkıştırılıp basınç ve sıcaklığı
yükseltilmiş olan havanın içerisine kolay tutuşabilen bir yakıtın püskürtülerek kendi
kendine tutuşturulabileceğini ve bu ilkeye göre bir motorun çalışabileceğini ileri
sürmüş ve 1892’de patent almıştır. Bu ilkeye göre ilk dizel motoru 1899’da Krupp
firmasında üretilmiştir. 1900’lerin başında bu ilk benzin ve dizel motorlarının
yapılmasından bu yana motorlar hızla yaygınlaşarak karayolu taşıtlarından gemilere,
trenlere, uçaklara ve tarım makinelerine kadar çok geniş bir alanda kullanılan en
yaygın ısıl makineler durumuna gelmiştir [4].
İki zamanlı motorlar konusunda ilk çalışma ise 1878 yılında İngiliz mühendis Sir
Dugald Clerk tarafından yapılmıştır. Bu motordaki emme ve egzoz işlemleri, dört
zamanlı motorlardaki emme ve egzoz supapları yerine, silindirin yan tarafında
bulunan, emme ve egzoz portları üzerinden olmaktaydı. Şekil 2.1’de Clerk’in yapmış
olduğu iki zamanlı motorun şeması görülmektedir.
4
Şekil 2.1. Clerk tarafından yapılan iki zamanlı motorun şeması [5]
1. Eksantrik 2. Krank mili 3. Güç pistonu 4. Egzoz portları 5. Sürgü valf 6.
Transfer kanalı 7. Süpürme pistonu
1891 yılında İngiltere’de Joseph Day tarafından, emme işlemi için karterden
sıkıştırmalı bir motor yapılmıştır. Bu motorda, karışım girişi ve egzoz çıkışı için
zamanlamaları piston ayarlamaktadır. Daha sonraları bu motorun gelişme süreci
başlamıştır [5].
İki zamanlı motorların otomobillerde kullanılması 1930’lu yıllarda başlamıştır. Bu
dönemde neredeyse tüm otomobil firmaları otomobillerinde iki zamanlı motorları
kullanmış veya denemeler yapmıştır. Bunların başında Wartburg, Trabant, Auto
Union, GM ve Saab gibi büyük firmalar gelmektedir. 1970 yılına kadar Wartburg ve
Trabant firmaları 127000 adet iki zamanlı motora sahip otomobil satmış, 1987’de bu
sayı 218000 adetle maksimum seviyesine ulaşmıştır [6].
İki zamanlı motorların modellenmesi üzerine yapılan çalışmaların çoğu akış ve
yanma süreçlerinin özellikleri üzerine olmuştur.
Ohyagi ve arkadaşları 1985 yılında türbülanslı yanma odası kullanan benzinli bir
motorda alev yayılımının modellemesini yapmışlardır. Bu çalışmada yanma odası
içindeki toplam kütle, yanmış gaz bölümü ve yanmamış gaz bölümü adı altında ikiye
5
bölünmüştür. Yanma odası boyunca basıncın üniform olduğu kabul edilmiştir.
Yanma odasındaki yanmış kütle bölümü, benzinli bir motorda çeşitli çalışma şartları
ve yanma odası geometrileri için zamanın bir fonksiyonu olarak ele alınmıştır. Bunu
yapmak için, yanmamış gazın yoğunluk değişiminin ve yanma odasındaki gaz akış
yapısının etkilerini içeren türbülanslı yanma modeli geliştirilmiştir. Hesaplanan
sonuçlar tek silindirli benzinli bir motorun kullanılmasıyla elde edilen deneysel
bilgilerle karşılaştırılmıştır. Önerilen model, alev yayılım işlemlerini iyi simule etmiş
ve şu sonuçlara varılmıştır:
1. Türbülent alev hızı ( U e ), laminer alev hızının toplamı olarak türetilmiştir ve
bölünmüş yanma odaları arasındaki gaz hızına ve bir de anlık yanmamış gaz
yoğunluğuna bağlı bir terimdir [7].
2. Girdap merkezindeki ateşlemeyle yüksek girdaplı yanma odası için türbülent alev
hızı, hız alanının homojenliğinden dolayı alevin konumuna bağlıdır [7].
Befrui ve Kratochwill tarafından 1990 yılında iki zamanlı benzinli ilmek süpürmeli
bir motorda yanma işleminin modellenmesi için çok boyutlu sayısal bir model
kullanılmıştır. Modelde verilen ilişki Şekil 2.2’de görülmektedir. Bu modelde silindir
gömleği çevresindeki emme portlarının düzenlemesi, egzoz portu boyunca çapla
ilgili yüzeylere göre simetriktir. Böylece, alanın hesaplanması silindir hacminin
yarısıyla sınırlandırılmıştır. Önerilen makalede şu sonuçlara varılmıştır:
1. Süpürme akışı yanma boyunca sürdürülebilir ama türbülans hızlı bir şekilde
azalır [8].
2. Alevle, ilmek süpürmeden arta kalan gazların güçlü etkileşimi, özellikle erken
yanma aşamalarında, alevin gelişimini belirgin şekilde etkiler [8].
3. Bujinin konumu, akış-alev etkileşiminin ve bundan kaynaklanan yanma
karakteristiklerinin dikkate alınmasıyla önem taşımaktadır [8].
6
Şekil 2.2. Simülasyon sonuçlarına göre yanma hacmi ve yüzeyi [8]
Kuo 1996 yılında benzinli bir motorda silindir basıncının sayısal modellemesini
yapmıştır. Bu izentropik gaz prosesi modelinde, McCustion, Lavoire ve Kaufmann
modeline bir orifis boyunca gaz akışı modelinin ilave edilmesiyle silindirdeki gaz
basıncının oldukça doğru bir şekilde tahmin edildiği belirtilmektedir. Modelin en
önemli kusuru, yanma boyunca yakıtın reaktivitesindeki değişimi hesaba
katmamasıdır [9].
Yıldız ve arkadaşları 2000 yılında yayınladıkları bir makalede benzinli bir motorun
en uygun çalışma koşulları ve performansını belirlemek için bir matematiksel model
geliştirdiklerini açıklamışlardır. Matematiksel modele uygun bir bilgisayar programı
geliştirilmiş, çeşitli hava fazlalık katsayısı, ateşleme avansı ve yanma süresi
kombinasyonları, gerçek motor gücünü sağlayacak koşullarda denenerek, optimum
hava fazlalık katsayısı, ateşleme avansı ve yanma süresi değerleri belirlenmiştir.
Enerji denklemleri kullanılarak sıkıştırma, yanma ve genişleme periyotlarında basınç
ve sıcaklığın birer derecelik krank mili açısına göre değişimleri belirlenmiştir. Buna
göre, model kullanılarak saptanan uygun çalışma koşullarında gerçek güç değeri ±
%1'den küçük bir hata ile hesaplanmıştır [10].
Moriyoshi ve arkadaşları 2001 yılında iki zamanlı doğru akışlı benzinli bir motorda
karışımın
hazırlanışının
nümerik
analizini
modellemişler, yüksek yükleme
şartlarında, daha yüksek püskürtme basıncının, gelişmiş atomizasyondan dolayı daha
iyi karışım değişikliklerine neden olduğunu, düşük yükleme şartlarında ise karışım
7
oluşumu için daha etkili olan piston duvarında, yakıt çarpması ve gaz hareketinden
dolayı püskürtme basıncının kesin bir değere ayarlanamadığını tespit etmişlerdir
[11].
Sekmen ve arkadaşları 2005 yılında yakıt olarak izo-oktan ( C8 H 18 ) kullanan tek
silindirli, 4 zamanlı, doğal emişli benzinli bir motorun ideal hava-yakıt çevrim
analizini incelemek üzere matematiksel bir simülasyon modeli geliştirmişlerdir. Bu
modelde, bir bilgisayar programı yardımıyla sıkıştırma oranı, motor hızı ve hava
fazlalık katsayıları için motorun krank açısına bağlı olarak silindir basınç ve sıcaklık
değişimleri elde edilerek ortalama indike basınç, yakıt ve hava tüketimleri, indike
güç, ısıl verim gibi bazı motor performans değerleri hesaplanmıştır. Hazırlanan
bilgisayar programı farklı motor hızları, sıkıştırma oranları ve hava fazlalık
katsayıları için çalıştırıldığında, şu tespitler yapılmıştır:
1. Maksimum silindir basınç ve sıcaklıkları, ortalama indike basınç, indike güç,
indike verim gibi parametreler sıkıştırma oranı artışıyla artmaktadır [12].
2. Artan motor hızı ile indike güç, ortalama indike basınç, hava ve yakıt tüketimleri
gibi parametreler bir noktaya kadar artmış ve daha sonra azalma göstermiştir
[12].
3. Sabit sıkıştırma oranında (8:1) hava fazlalık katsayısı artırıldığında (0,95-1,05
aralığında 0,05 birimlik adımlar halinde); silindir basınç ve sıcaklıkları, ortalama
indike basınç, indike güç, yakıt tüketimi parametreleri azalmış, karışım
fakirleştikçe ideal gaz özelliklerine yaklaştığından ısıl verim ve hava tüketimi
artmıştır [12].
Mitianiec ve Forma 2008 yılında iki zamanlı tek silindirli direkt enjeksiyonlu bir
motora ait karışım oluşumunu modellemişlerdir. Bu makalede, tepedeki direkt
püskürtme karışım oluşumunda dikkate alınmıştır. Piston tepesi dairedir ve yanma
odası yarım küreden oluşur. Her iki transfer portu, egzoz portu merkezi ve silindir
8
eksenine nazaran simetriktir. Ağ üretimi ve simülasyon, ön işlemci KIVA3V ile
yapılmıştır. Püskürtme boyunca fiziksel işlemlerin modellemesi bir deneysel
kurulum varsayımıyla gerçekleştirilmiştir. Püskürtme ve yanmanın diferansiyel
denklemleri KIVA programıyla çözümlenmiştir. Püskürtülen yakıtın sıvı ve gaz
hallerinin dağılımını gaz hızının etkilediği anlaşılmıştır. Silindirdeki karışımın farklı
fazlardaki hareketi şu genel eşitlikle ifade edilmiştir [13]:
∂ (ri..ρi..ϕi )
+ V (ri..ρi .ui .ϕi − ri .Γϕi .gradϕi ) = ri .Sϕi
∂t
(2.1)
Burada;
ρi
: Faz yoğunluğu
ϕi
: Entalpi, gaz hareketinin momentumu, türbülans enerjisi gibi faz özellikleri
ui
: Fazın hız vektörü
Γϕi
: Fazdaki ϕ değerinin difüzyon katsayısı
Sϕi
: ϕi değişiminin kaynak terimi
V
: Nable operatörü
şeklinde tanımlanmıştır. Mitianiec ve Forma tarafından modellenen sayısal ağ Şekil
2.3’de görülmektedir.
9
Şekil 2.3. İki zamanlı bir motorun sayısal çözüm ağı [13]
Mikalsen ve Roskilly 2008 yılında elektrikli güç jeneratörü ile çalışan sıkıştırma ile
ateşlemeli serbest pistonlu iki zamanlı bir motorun tasarım ve simülasyonuna dair bir
model geliştirmişlerdir. Bu çalışmada simülasyon programı, motor girdi değişkenleri
ve tasarım parametrelerinin etkisini incelemek için MATLAB sayısal hesaplama
yazılımı kullanarak yazılmıştır. Pistonun hareketi, piston hızı ve pozisyonunu veren
Euler sayısal integrasyonunun kullanılmasıyla çözülmüştür. Program hem sabit
durum çıkışlarını, hem de motor performansının geçici etkilerini incelemeye olanak
sağlamaktadır. Geliştirilen programdan elde edilen silindir basıncı-piston pozisyonu
ve gaz sıcaklığı-zaman diyagramları Şekil 2.4 ve 2.5’te görülmektedir [14].
Şekil 2.4. Silindir basıncı-piston hareketi diyagramı [14]
10
Şekil 2.5. Gaz sıcaklığı-zaman diyagramı [14]
Sekmen P. ve Sekmen Y. 2007 yılında benzinli bir motorun gerçek hava-yakıt
çevrim
analizini
incelemek
üzere
matematiksel
bir
simülasyon
modeli
geliştirmişlerdir. Bu modelde, doğal emişli Otto çevrimine göre çalışan tek silindirli
dört zamanlı bir motorun çevrim analizini incelemek için FORTRAN programlama
dilinde matematiksel bir simülasyon modeli geliştirilmiştir. Program çalıştığında
aşağıdaki sonuçlar gözlenmiştir:
1. Maksimum silindir basıncı ve sıcaklığı motor hızı arttıkça artmış, ortalama
efektif basınç ve ısıl verimin tepe değerleri 2400 1/min’de elde edilmiş ve daha
sonra azalmaya başlamıştır [15].
2. Silindir basınç ve sıcaklığı, ortalama efektif basınç, efektif güç ve özgül yakıt
tüketimi hava fazlalık katsayısının artmasıyla azalmıştır [15].
3. Program, silindir ölçüleri ve silindir giriş şartlarını değiştirebilmesi sayesinde
motor performanslarının karşılaştırılmasını yapabilir. Program ayrıca değişik gaz
kelebeği açıklıklarındaki sıkıştırma oranı, egzoz gaz geri dönüşümü ve egzoz
emisyonun ilave edilmesiyle bir çalışma yapmak için de uygundur [15].
Simülasyona göre hava fazlalık katsayısının silindir basıncına ve sıcaklığına etkisi
Şekil 2.6 ve Şekil 2.7’de görülmektedir.
11
Şekil 2.6. Hava fazlalık katsayısının silindir basıncına etkisi [15]
Şekil 2.7. Hava fazlalık katsayısının gaz sıcaklığına etkisi [15]
Semin ve arkadaşları 2008 yılında dinamik ağ kullanarak piston portlu motorlarda
silindir içindeki akışı modellemişlerdir. Bu modelde iki zamanlı benzinli karşı akışlı
bir motorun üç boyutlu analizi için sayısal bir analiz sunulmuştur. Modelde yüksek
devirlerde düşük devirlere göre daha yüksek silindir basıncının oluşacağı sonucuna
varılmıştır. Simülasyon sonucuna dayalı olarak, silindir basınç değerleri farklı hızlar
için krank mili açısının bir fonksiyonudur. Simülasyon sonucunda elde edilen ve
12
silindir basıncının motor hızına bağlı olarak değişimini gösteren krank mili açısısilindir basıncı diyagramı Şekil 2.8’de görülmektedir [16].
Şekil 2.8. Krank mili açısı-silindir basıncı diyagramı [16]
Motoyama ve Gotoh 1985 yılında iki zamanlı motorlarda yüksek sıkıştırma oranının
etkisini incelemek üzere bir model geliştirmişlerdir. Modelde, yüksek sıkıştırma
oranının, iki zamanlı hava soğutmalı bir motosiklet motorun çıkış gücü ve özgül
yakıt tüketimi üzerindeki etkileri incelenmiştir. Modelde şu sonuçlara varılmıştır:
1. Çeşitli kayıplardan dolayı, beklenen teorik değerlere ulaşmak için iyileşme
oranının yeterli olmamasına rağmen, yüksek sıkıştırma oranıyla yakıt tüketimini
iyileştirmek mümkündür [17].
2. Düşük yüklerde kayıplardaki artış, artan kısa devre, artan mekanik kayıplar ve
soğutma kayıpları ile açıklanabilir. Ağır yüklerde, zaman kaybı artar ama kısa
devrenin etkisiyle birlikte mekanik kayıplar ve soğutma kayıpları azalır. Çalışma
gazlarının değişken özgül ısı oranı, kayıpları kontrol altına almak için etkili bir
tedbirdir [17].
13
3. Yüksek sıkıştırma oranı, artan ısı kayıpları ve vuruntuya rağmen çıkış gücünü
iyileştirmeyi mümkün kılar [17].
14
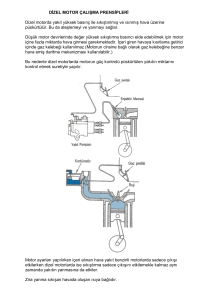
3.
İKİ ZAMANLI MOTORLAR
3.1.Çalışma Prensipleri
Krank milinin tam bir devrinde, diğer bir deyimle pistonun iki stroğunda bir iş
çevrimi oluşturan makinelere iki zamanlı motor adı verilir. İki zamanlı motorlarda
karışım silindire silindir gövdesine açılmış portlardan girerken, gazların atılışı, yine
silindir gövdesi üzerine açılmış egzoz portları veya egzoz supapları üzerinden
olmaktadır. Şekil 3.1’de iki zamanlı bir motorun gaz değişim diyagramı, Şekil 3.2’de
iki zamanlı bir benzinli motorun çalışması şematik olarak gösterilmiştir.
Şekil 3.1. İki zamanlı bir motorun gaz değişim diyagramı [18]
a)
b)
c)
Şekil 3.2. İki zamanlı benzinli bir motorun çalışmasının şematik gösterimi
a) Sıkıştırma, Kartere emme b) Genişleme, Karterde sıkıştırma c) Süpürme
15
3.1.1. Sıkıştırma işlemi
Piston AÖN’da iken silindir içerisi taze karışım (yakıt-hava karışımı) ve artık egzoz
gazları ile doludur. Piston ÜÖN’ya giderken daha yüksek olan egzoz portları
kapanıncaya kadar etkin bir sıkıştırma olmaz. Taze karışımın bir bölümü egzoz
portlarından dışarı kaçar. Bu durum iki zamanlı benzin motorlarının verimlerinin
düşük olmasının temel nedenidir. Egzoz portları kapandıktan sonra etkin sıkıştırma
başlar. Politropik sıkıştırma sonunda gazların basınç ve sıcaklığı artar. Taze
karışımın içindeki yakıt buharlaşır ve tutuşmaya hazır duruma gelir. Burada
geometrik olarak strok hacmi Vh olmakla birlikte, egzoz portlarının yüksekliği
nedeniyle ΔVh kadar hacim kaybı olur ve etkin strok hacmi Vh' olur. Bu da iki
zamanlı motorların gücünün iki kat olamamasının diğer bir nedenidir. Pistonun üst
tarafı sıkıştırma yaparken alt tarafı karter boşluğu ve vakum oluşturur. Piston
ÜÖN’ya yaklaştığında reed valften kartere yakıt hava karışımı dolar. Sıkıştırma
sonunda;
Basınç;
Benzin motorlarında 10-14 bar
Dizel motorlarında
30-50 bar
Sıcaklık;
Benzin motorlarında 550-750 K
Dizel motorlarında
700-900 K
olur [19].
3.1.2. Yanma ve genişleme işlemi
Piston ÜÖN’ya yaklaşırken ateşleme avansı kadar önce bujide elektrik kıvılcımı
oluşturulur. Yanmaya bağlı olarak küresel bir alev cephesi oluşur ve hızlı bir şekilde
genişler. Yanma 1/1000 saniye kadar sürdüğünden bu sırada piston çok az hareket
16
edebilir. Bu nedenle, yanmanın yaklaşık olarak sabit hacimde olduğu varsayılabilir.
Yakıtın yanma ısısı açığa çıkar ve sıcaklık ve basınç birdenbire artar. Oluşan basınçlı
yanmış gazlar pistonu hızla AÖN’ya iter, hacim artar ve politropik genişleme olur.
Krank milinden döndürme momenti ve yararlı iş elde edilir. Bu arada pistonun alt
yüzü, kartere daha önceden dolmuş olan yakıt-hava karışımını biraz sıkıştırır. Piston
AÖN’ya yaklaştığında, önce egzoz portları açılır. 0,3-0,5 MPa basınçlı yanmış gazlar
egzoz kanalından hızla dışarıya boşalmaya başlar ve basınç hızlı bir şekilde düşer.
Bunun ardından süpürme portları da açılır. Karterde biraz sıkıştırılmış olan taze
karışım süpürme portlarından silindire gelerek, geriye kalan egzoz gazlarını süpürür
ve dışarıya atar. Taze karışımı yönlendirerek daha iyi bir süpürme sağlamak amacı
ile süpürme portları hafif alttan yukarı ve teğetsel olarak açılabilir ve piston
tablasının üst tarafı hafif çıkıntılı yapılabilir. Süpürme yapılırken taze karışımın bir
bölümü egzoz gazları ile dışarı kaçabilir. Ayrıca akım çizgilerinin ulaşamadığı ölü
noktalarda artık egzoz gazları bulunabilir. Bu da iki zamanlı benzin motorlarının
verim ve güç düşüklüğünün başka bir nedenidir. Böylece pistonun iki hareketi veya
krank milinin bir tam turu sonunda bir iş çevrimi tamamlanmış olur.
İki zamanlı motorlarda, portların açılma ve kapanma süreleri ile ateşleme veya
püskürtme avanslarının önemi büyüktür. İki zamanlı motorların supap zamanları ve
ateşleme avansları aşağıdaki değerler arasında değişmektedir [19].
Egzoz Portları
Emme Portları
Ateşleme Avansı
EGAA
50-60 ° K.M.A.
AÖN’dan önce
EGKG
50-60 ° K.M.A.
AÖN’dan sonra
EMAA
30-40 ° K.M.A.
AÖN’dan önce
EMKG
30-40 ° K.M.A.
AÖN’dan sonra
A.A.
10-20 K.M.A.
°
ÜÖN’dan önce
17
Egzoz ve emme portlarının açılma avansları ve kapanma gecikmeleri aynı ise
simetrik; farklı ise asimetrik olarak adlandırılır.
3.2.Port Zaman Diyagramları
İki ve dört zamanlı motorların tümünde, bir iş çevrimi için emme, sıkıştırma, yanmagenişleme ve egzoz süreçleri gereklidir. İki ve dört zamanlı motorlar arasında
termodinamik olaylar bakımından hiç bir fark yoktur. Fark, karışımın silindirlere
alınışı ve egzoz gazlarının silindirlerden atılışındadır. Egzoz gazlarının silindirlerden
atılışı ve süpürme havası veya karışımının silindirlere verilişi, port zaman diyagramı
denilen diyagramlar üzerinden açıklanmaktadır. Şekil 3.3’ de iki zamanlı benzinli bir
motorun port zaman diyagramı görülmektedir.
Şekil 3.3. İki zamanlı benzinli bir motorun port zamanlama diyagramı [20]
3.3. İki ve Dört Zamanlı Motorların Kıyaslanması
İki zamanlı motorların yararları ve sakıncaları, dört zamanlılarla karşılaştırmalı
olarak şu şekilde özetlenebilir:
1. Dört zamanlı motorlara göre, eşit ana boyutlar (silindir çapı ve piston stroku),
silindir sayısı ve devir sayılarında teorik olarak iki misli güç üretirler. Böylelikle,
18
aynı güç için iki zamanlı motorların özgül ağırlığı ve boyutları dört zamanlı
motorlarınkinden önemli şekilde küçük olur [20].
2. Özellikle silindir sayısının dörtten fazla olduğu motorlarda, krank milinin
moment dalgalanmalarına karşı iyi dengelenmesi nedeniyle ağır bir volana gerek
yoktur. Yüksek devirli dört zamanlı motorlar ise düzgün çalışma sağlayabilmek
için daha ağır volanlar gerektirirler [20].
3. İki zamanlı motorlarda dört zamanlı motorlara göre daha yüksek mekanik verim
değerleri sağlanmaktadır [20].
4. İki zamanlı motorların dört zamanlı motorlara göre bir başka üstünlüğü de
yapılarındaki sadeliktir. Özellikle dört zamanlı motorlarda supap mekanizmasının
karmaşık yapıda oluşu ve çok gürültülü işletmeye neden olması, dikkate alınması
gereken önemli bir sakıncadır [20].
5. İki zamanlı motorlarda yeterli olmayan süpürme havası veya karışımı
kullanıldığında, silindirler egzoz gazlarından iyi temizlenememekte, ayrıca
silindirler iyi şarj edilmediklerinden, dört zamanlılara oranla daha küçük
ortalama basınçlar elde edilmektedir. Diğer yandan, fazla süpürme karışımı
kullanıldığında ise karışım kaybı olmakta, yakıt ekonomisi kötüleşmektedir. [20].
6. İki zamanlı motorların egzoza olan karışım kaybı nedeniyle ısı kayıpları daha
fazla
ve
egzoz
emisyonları
daha
kötüdür
ve
genellikle
standartları
karşılayamamaktadır [20].
7. İki zamanlı motorlarda süpürme etkinliğini artırmak üzere yetersiz susturucu
kullanılmakta, bu nedenle egzoz gürültüsü daha fazla olmaktadır [20].
19
3.4. Süpürme Teorisi
İki zamanlı motorlarda silindirin egzoz gazlarından temizlenmesi olayına süpürme
adı verilir. Dört zamanlı motorların silindirlerinin egzoz gazlarından temizlenmesi
piston tarafından cebren sağlanır. Egzoz zamanının sonuna doğru oluşturulan supap
bindirmesi de yanma odasının atık gazlardan temizlenmesinde yardımcı olur. İki
zamanlı
motorlarda ise pistonun egzoz gazlarını süpürmesi söz konusu
olmadığından, silindirlerin egzoz gazlarından temizlenmesinde atmosfer basıncından
biraz daha yüksek basınçtaki hava veya karışımın süpürme etkisinden yararlanılır.
İki zamanlı motorlarda silindirlerin egzoz gazlarından temizlenmesi ve temiz hava
veya karışımla doldurulması, yakıt ekonomisi ve yüksek verim sağlanmasını olumlu
etkiler. Bu amaca yönelik olarak iki zamanlı motorlarda iki ayrı süpürme yöntemi
kullanılmaktadır. Bunlar dönüş veya ters akışlı süpürme ve doğru akışlı süpürmedir.
Doğru akışlı süpürme, hava-yakıt karışımının emme portundan girdiği, egzoz
gazlarının egzoz supaplarından çıktığı iki zamanlı motorlarda kullanılmaktadır [21].
Bu çalışmada sadece ters akışlı süpürme dikkate alınmıştır.
3.4.1. Dönüş (ters) akışlı süpürme
Bu tür süpürmede hava veya karışımın silindire verilişi ve egzoz gazlarının atılışı,
silindirlerin gövdeleri veya gömleklerine açılmış portlar yardımıyla sağlanır. Hava
veya karışım, süpürme portlarından silindirlere verilir, silindir kapağına doğru
yükselir ve ona çarparak geriye döner. Bu arada önüne kattığı gazları da egzoz
portlarından silindir dışına atar. Hava veya karışım akımı yönünün önce yukarı, sonra
aşağıya doğru oluşu nedeniyle bu süpürme yöntemine “Dönüş (Ters) Akışlı
Süpürme” denir [21]. Şekil 3.4’te Dönüş (ters) akışlı süpürme görülmektedir.
20
Şekil 3.4. Dönüş (ters) akımlı süpürme [21]
21
4.
TEORİK ÇEVRİM ANALİZİ
İçten yanmalı motorlarda çevrimin termodinamik analizi karmaşık simülasyonlarla
yapılabileceği gibi basit hava standart çevrimleriyle de yapılabilmektedir. Teorik
motor çevrimleri, motorların silindirleri içindeki olayları basit şekilde gösteren bir
yaklaşımdır. Teorik motor çevrimleri aracılığıyla tasarlanacak motorların performans
parametreleri yaklaşık olarak önceden belirlenebilir ve farklı motorlar arasında
karşılaştırma yapılabilir.
4.1. İki Zamanlı Motorların Hava Standart Otto Çevrimi
Teorik motor çevrimlerinde birçok varsayımlar ve basitleştirmeler yapılır ve teorik
motor çevrimlerinin hesabı sonunda bulunan sonuçların incelenmesiyle motor
silindirleri içindeki olayların yapısı daha iyi anlaşılır. Teorik motor çevrimlerinde
uygulanan başlıca varsayımlar şunlardır:
1. Teorik çevrimlerde silindir içinde sabit miktarda karışımın bulunduğu varsayılır.
Gerçekte motorun çalışabilmesi için dışarıdan taze hava-yakıt karışımının
emilmesi ve yanma sonunda yanmış egzoz gazlarının dışarı atılması gerekir [22].
2. Motor
çalışırken
gazların
özgül
ısılarının
sabit
kaldığı
varsayılır,
( cv = sabit , c p = sabit ). Halbuki motorlarda gerçekte sıcaklıklar önemli düzeyde
değiştiği için gerçek çevrim hesaplarında özgül ısıların sıcaklıkla değiştiği hesaba
T
katılmalıdır ( cv =
1
( A + 2 BT )dT ) [22].
T 2 ∫0
3. Teorik motor çevrimlerinde sıkıştırma ve genişleme işlemlerinin çevre ile ısı
alışverişi olmadan (adyabatik) gerçekleştirildiği varsayılır. Gerçekte ise
sıkıştırma ve genişleme işlemleri boyunca çevre ile sürekli ısı alışverişi olur [22].
22
4. Gerçekte sıkıştırma ve genişleme işlemleri adyabatik değil politropik karakterde
işlemlerdir [22].
Teorik: PV k a = sabit
(4.1)
= sabit
(4.2)
Gerçek: PV
np
5. Teorik çevrimlerde sisteme Q1 ısısının verildiği düşünülür. Gerçekte ise Q1 ısısı
değişik hidrokarbonların karışımı olan sıvı veya gaz yakıtların, havanın oksijeni
ile yanması sonunda açığa çıkar. Yanma boyunca silindir içindeki gazların
basınç, sıcaklık ve hacimleri sürekli değişir, çevre ile ısı alışverişi olur,
türbülanslı yapıda gaz hareketleri olur, yüksek sıcaklık etkisiyle karmaşık yapılı
birçok zincirleme kimyasal reaksiyon meydana gelir, gazların yapısı değişir [22].
6. Teorik çevrimlerde sıkıştırma, yanma ve genişleme gibi işlemlerin tam ölü
noktalarda başlayıp bittiği varsayılır. Bunun sonucunda teorik motor çevrimleri
keskin, köşeli eğriler şeklinde olur. Gerçekte ise emme veya egzoz portları
avanslı (öncelikli) olarak açılır ve gecikmeli olarak kapatılır. Ateşleme veya
püskürtme avanslı olarak başlatılır. Yanma bir anlık olmaz belirli bir süre devam
eder. Bütün bunların sonucunda gerçek motor çevrimleri köşeli değil de
yuvarlatılmış karakterde olur [22].
7. Teorik çevrimlerde silindir içinde oluşan gaz basıncının ve pistona etki eden
kuvvetlerin kayıp olmaksızın krank milinde döndürme momentine dönüştüğü
varsayılır. Gerçekte piston ile silindir duvarları arasında, yataklar gibi tüm
hareketli motor elemanlarında sürtünme kayıpları ve gaz kaçakları olur. Su
pompası, yağ pompası, fan, şarj dinamosu gibi yardımcı donanımlar motorun
ürettiği işin bir bölümünü harcar. Homojen olmayan karışımdan dolayı tam
olmayan yanma gerçekleşebilir. Ayrıca egzoz ve emme işlemlerinde (karışım
değişimi işlemlerinde) iş harcanır. Bütün bu kayıplar mekanik kayıplar işi
şeklinde göz önüne alınmalıdır. Teorik çevrimlerde mekanik kayıplar göz önüne
alınmaz [22]. Şekil 4.1’de hava standart otto çevrimi görülmektedir.
23
Şekil 4.1. Hava standart otto çevrimi
Şekil 4.1’den de görüleceği gibi hava standart otto çevriminde:
a − c arasında izentropik sıkıştırma işlemi,
c − Z arasında sabit hacimde ısı girişi,
Z − b izentropik genişleme işlemini,
b − a arasında sabit hacimde ısı çıkışı
gerçekleşir.
Pa ve Ta biliniyorsa ayrıca Q1 ısısı veya Pz basıncı gibi bir değer verilmişse ve
motorun sıkıştırma oranı da biliniyorsa termodinamik bilgilerden yararlanarak c, Z, b
noktalarının basınç ve sıcaklıkları hesaplanabilir. Ayrıca Q2 ısısı ve çevrim işi
( Wç = Q1 − Q2 ) hesaplanabilir. Böylece ısıl verim (ηt = Wç / Q1 ) hesaplanabilir.
ηt =
Wç Q1 − Q2
q
=
=1− 2
Q1
Q1
q1
(4.3)
C − Z durumları arasında sisteme sabit hacimde ( Q1 ) ısı girişi meydana gelmektedir.
Sisteme giren ısı miktarı;
24
Q1 = mcV (TZ − TC )
(4.4)
q1 = cv (Tz − Tc )
(4.5)
b − a durumları arasında sistemden çevreye ısı geçişi olmaktadır. Sistemden çıkan ısı
Q2 ile gösterilirse;
Q2 = mcv (Tb − Ta )
(4.6)
q2 = cv (Tb − Ta )
(4.7)
Bu durumda ısıl verim;
ηt = 1 −
q2
c (T - T )
T (T / T − 1)
=1− v b a =1− a b a
q1
c v (Tz - Tc )
Tc (Tz / Tc − 1)
(4.8)
olur. a-c ve z-b hal değişimlerinin izentropik ve va = vb , vc = vz olduğu göz önüne
alınırsa;
Ta ⎛ vc ⎞
=⎜ ⎟
Tc ⎜⎝ va ⎟⎠
k a −1
⎛v ⎞
= ⎜⎜ z ⎟⎟
⎝ vb ⎠
k a −1
=
Tb
Tz
(4.9)
olur. Bu bağıntılar ısıl verim denkleminde yerine konur ve basitleştirilirse;
ηt = 1 −
1
ε
k a −1
(4.10)
olur. Çevrimi inceleyebilmek için motorun sıkıştırma oranının ve silindire sokulan ısı
miktarı veya yanma sonu basınç ve sıcaklığı gibi bazı özelliklerinde bilinmesi
gerekir.
25
Sıkıştırma oranı;
ε=
Va Vc + Vh
V
=
= 1+ h
Vc
Vc
Vc
(4.11)
Basınç artma oranı;
λ=
Pz
Pc
(4.12)
4.2. Çevrimin İncelenmesi
4.2.1. Sıkıştırma işlemi (a-c)
a − c durumları arasında adyabatik sıkıştırma işlemi gerçekleştirilir.
Va = Vb
(4.13)
Vc = Vz
(4.14)
Pc = Paε k a
(4.15)
Tc = Taε k a −1
(4.16)
olur.
4.2.2. Sabit hacimde yanma (c-Z)
c − Z durumları arasında sisteme sabit hacimde ısı girişi meydana gelmektedir.
26
Pz = λPc = λPaε k a
(4.17)
Tz = Tc λ = Ta λε k a −1
(4.18)
olur.
4.2.3. Genişleme işlemi (z-b)
z − b durumları arasında izentropik genişleme işlemi meydana gelmektedir.
Pb =
Tb =
olur.
Pz
εk
Tz
εk
(4.19)
a
a
−1
(4.20)
27
5.
GERÇEK ÇEVRİM HESAPLAMALARI İÇİN ANALİTİK MODEL
Teorik çevrimler incelenirken birçok varsayımlar yapılmıştı. Bu varsayımların
sonucunda teorik çevrim köşeli karakterde olur. Ayrıca teorik çevrimde egzoz ve
emme işlemleri yer almaz. Gerçek çevrimde sıkıştırma ve genişleme boyunca çevre
ile ısı alışverişi olur. Gazların özgül ısıları sıcaklığa bağlı olarak sürekli değişir.
Yanma boyunca karmaşık kimyasal reaksiyonlar ve akım karışıklıkları olur. Çeşitli
sürtünmeler, mekanik kayıplar ve gaz kaçakları olur. Motorun çalışabilmesi için
yanmış gazlar dışarı atılır ve dışarıdan taze karışım emilir. Ayrıca yanma tam üst ölü
noktada başlamaz. Ateşleme ÜÖN’dan biraz önce avanslı olarak başlatılır. Portlar
tam ölü noktalarda açılıp kapatılmaz, avanslı olarak açılır, gecikmeli olarak kapatılır.
Bunun sonucunda gerçek çevrim köşeli değil de yuvarlatılmış karakterde olur.
5.1. Gerçek Motor Çevrimlerindeki Sınırlamalar
Gerçek motor çevrimlerinde birçok karmaşık olay vardır. Bunlar sıkıştırılabilir akış,
yanma, türbülanslı iç akımlar, ısı transferi ve sürtünme olaylarıdır ve bu olayları tam
teorik şekilde modellemek güçtür. Burada belirli yaklaşımlarla geliştirilmiş olan bir
yöntem tanınacaktır. Bu yöntemde uygulanacak başlıca varsayımlar şu şekilde
özetlenebilir:
1. Gerçek motorlarda emme olurken sıkıştırılabilir bir akışkan olan hava kesiti
değişen emme kanallarından geçer ve benzin motorlarında havanın içersine
ayrıca yakıt püskürtülür. Bu yakıt kısmen buharlaşır, gaz kelebeği yarı kapalı
durumda olabilir. Bütün bu etkiler göz önüne alarak emme olayını modellemek
güçtür. Çevrim hesabında emilen havanın sıkıştırılabilme özelliğinin çok az
olduğu varsayılarak, bernoulli denkleminden yararlanarak emme boyunca ΔPa
basınç düşüşünün olduğu düşünülmüştür. Emme boyunca bütün kısılma ve
sürtünme kayıpları bir β 2 + ξ toplam kayıp katsayısı ile göz önüne alınmıştır.
Böylece emme sonu basıncı doğal emişli motorlarda P1 = P0 − ΔPa olur. Emme
28
sonu sıcaklığı emilen taze karışımın ve artık egzoz gazlarının sabit basınç altında
karıştıkları düşünülerek bir ortalama sıcaklık şeklinde hesaplanmıştır. Egzoz
işlemi ise gazların egzoz portuntan hızla boşaldığı düşünülerek Pr ve Tr arasında
yazılan yarı amprik bir bağıntıdan yararlanılarak değerlendirilmiştir [22].
2. c p , cv özgül ısılarının sıcaklıkla lineer değiştiği varsayılarak ortalama özgül ısı;
T
1
cv = 2 ∫ ( A + 2 BT )dT
T 0
(5.1)
bağıntısıyla hesaplanmıştır. Her gaz için A ve B katsayıları özgül ısı tablolarına
eğri uydurarak elde edilmiştir [22].
3. Gerçekte sıkıştırma ve genişleme işlemleri politropik karakterdedir. Sıkıştırma ve
genişleme boyunca silindir içindeki gazların sıcaklıkları sürekli değişir. Sıcak
motor duvarlarından gazlara veya gazlardan duvara ısı geçişi olur. Bu nedenle
gerçekte sıkıştırma ve genişlemenin her adımında ayrı bir n politrop üssü geçerli
olur. Çevrim hesabında sıkıştırmanın sabit bir n1 politrop üssüyle, genişleme
işleminin de sabit bir n2 politrop üssüyle gerçekleştiği varsayılmıştır [22].
4. Yakıt, yanma süresince havanın oksijeni ile zincirleme reaksiyonlara girer.
Türbülanslı akım karışıkları ve silindir duvarlarına ısı transferi olur. Bu arada
yanma odasının hacim, basınç ve sıcaklıkları sürekli olarak değişir. İçerideki
gazların yapısı değişir ve yanma ısısı açığa çıkar. Yanma işlemindeki bütün
kayıplar, yanmada ısıdan yararlanma verimi ξ z ile göz önüne alınmış ve 1 kg
yakıtın yanması sonunda sisteme verilen ısı;
θ1 = ξ z H u
ifadesiyle hesaplanmıştır [22].
(5.2)
29
5. Gerçek motorlarda çeşitli mekanik kayıplar görülür. Çevrim hesabında bütün
mekanik kayıplara karşılık gelen mekanik kayıplar ortalama basıncı aşağıdaki
bağıntılar ile göz önüne alınmıştır.
Pmm = a + bV p
(5.3)
Burada V p ortalama piston hızıdır ve
Vp =
Hn
(m/s)
30
(5.4)
bağıntısıyla bulunur [22].
6. Çevrim hesabında piston ile silindir duvarları arasında segmanlardan gaz
kaçaklarının olmadığı varsayılacaktır. Gerçekte motorun yıpranma durumuna
göre silindirlerden dışarıya doğru az veya çok gaz kaçakları meydana gelir [22].
5.2. Krank Mili Açısına Göre Piston Pozisyonu
Çevrimlerin P-V ve P-Q diyagramlarının çizilebilmesi için, sistemin uygun krank
açılarındaki durumunun hesaplanması gerekmektedir. Şekil 5.1’de içten yanmalı
motorlar için krank-piston-biyel geometrisi görülmektedir.
30
Şekil 5.1. İçten yanmalı motorlar için piston-krank-biyel geometrisi
Şekil 5.1’den yararlanarak piston yolu;
s = l + r (1 − cosθ ) − l 2 − (r sin θ ) 2
(5.5)
ifadesinden belirlenebilir [23]. Burada;
l
: Biyel boyu, (m)
r
: Krank yarıçapı, (m)
θ
: Krank mili açısı, ( ο )
Anlık silindir hacmi ise,
Vs = Apis s + Vc =
πd pis 2
4
s + Vc
ifadesinden belirlenebilir. Burada;
Apis
: Piston alanı, (m2)
Vc
: Yanma odası hacmi, (m3)
d pis
: Piston çapı, (m)
s
: Piston yolu, (m)
(5.6)
31
Süpürme hacmi için;
Vsv = z
π
4
d pis H
(5.7)
ifadesi yazılabilir [24]. Burada;
d pis
: Piston çapı, (m)
H
: Strok, (m)
z
: Silindir sayısı
5.3. Çevrim İşlemleri
Benzinli iki zamanlı bir motorun gerçek çevrimine ait basınç-hacim diyagramı Şekil
5.1’deki gibi gösterilebilir.
Şekil 5.2. İki zamanlı bir motorda gerçek basınç-hacim diyagramı
Çevrim aşağıdaki işlemlerden oluşmaktadır:
1-2 eğrisi sıkıştırma işlemi
2-3 eğrisi yanma işlemi
32
3-4 eğrisi genişleme işlemi
4-5 eğrisi egzoz açılma işlemi
5-a-6 eğrisi karışımla süpürme işlemi
6-1 eğrisi pistonla süpürme işlemi
5.3.1. Süpürme işlemi
Süpürme basıncı
İki zamanlı motorlarda, dört zamanlı motorlardan farklı olarak yakıt-hava karışımı,
atmosfer basıncının üstünde bir basınçla ( P5 =1,1-1,4 bar) silindire verilir. Verilen bu
karışıma süpürme karışımı denilir ve basıncı çeşitli yollarla sağlanır.
İki zamanlı motorlarda, A.Ö.N’daki yakıt-hava karışımının süpürme basıncı,
süpürme portlarındaki akış kayıplarından dolayı süpürme karışımının basıncına göre
biraz düşüktür. Yakıt-hava karışımının A.Ö.N’daki basıncı;
Pa =
P5 + Peg
(bar)
2
(5.8)
Burada Peg egzoz sisteminin geri basınç farkıdır ve iki zamanlı motorlarda;
Peg = 0,06 (bar)
(5.9)
değerini alır [25].
Süpürme işlemi boyunca oluşan bütün kayıplar nedeniyle Pa basıncına göre ΔPa
kadar bir basınç düşüşü meydana gelir. Bu basınç düşüşü;
33
⎛V n ⎞ ρ
ΔPa = ( β 2 + ζ )⎜⎜ m ⎟⎟ 10− 6 (bar)
⎝ nN ⎠ 2
(5.10)
eşitliği ile bulunur. Burada;
β2 +ζ
: Kısılma ve sürtünme kayıpları, (2,5-4)
Vm
: En dar kesitteki hız, (50-130 m/s)
ρ
: Havanın yoğunluğu, (1,2 kg/m3)
n
: Motor hızı, (1/min)
Böylece süpürme sonu basıncı;
P1 = P5 − ΔPa
(5.11)
olur.
Süpürme karışımı sıcaklığı
İki zamanlı motorlarda süpürme sonunda, yakıt-hava karışımının sıcaklığı dört
zamanlı motorlarınkinden biraz farklıdır. Yakıt-hava karışımının sıcaklığı, karterden
sisteme girerken artar ve
T1 = T0 ( P1 / P0 )
( n p −1) / n p
(5.12)
olur. Burada np karterin politropik sıkıştırma üssüdür ve iki zamanlı yüksek devirli
motorlarda;
np=1,36-1,4
aralığındadır. Yakıt-hava karışımının AÖN’daki sıcaklığı ise;
(5.13)
34
Ta =
T1 + ΔT + γ rTr
1+ γr
(5.14)
olur. Burada;
ΔT
: Taze karışımın ön ısınması, (10°C)
γr
: Artık gazlar katsayısı, (0,2-0,3)
Tr
: Artık gazların sıcaklığı, (1100 K)
Artık egzoz gazları
Süpürme işleminin başlangıcında silindir içerisinde bir önceki çevrimden kalmış olan
artık egzoz gazları bulunur. Süpürme işleminin başlangıcında silindir içerisinde
bulunan artık egzoz gazlarının kilomol sayısının, süpürme işlemi sonunda silindire
dolacak olan taze karışımın kilomol sayısına oranına artık egzoz gazları katsayısı
denir ve γ r ile gösterilir. Karterden süpürmeli iki zamanlı motorlarda;
γ r = 0,20 − 0,30
(5.15)
değerleri arasındadır. Artık egzoz gazları basıncı ise iki zamanlı motorlarda,
Pr = (1,1 − 1,25) P5 (bar)
(5.16)
eşitliği ile bulunur.
Hacimsel verim
Süpürme işlemi sonunda silindire gerçekte dolacak olan gazların kilomol sayısının,
kayıpsız emme durumunda dış ortam koşullarında dolabilecek gazların kilomol
sayısına oranına hacimsel verim denir ve;
35
ηv =
ε
P1
T0
ε − 1 P0 T0 + ΔT + γ rTr
(5.17)
eşitliği ile bulunur. İki zamanlı karterden süpürmeli motorlarda hacimsel verim;
ηv = 0,50 − 0,70
(5.18)
aralığındadır.
5.3.2. Sıkıştırma işlemi
Gerçek motor çevrimlerinde sıkıştırma işlemi çevre ile ısı alış verişi olduğu için
politropik karakterdedir. Sıkıştırma işlemi boyunca sıcak duvarlardan içerideki
gazlara, içerideki gazlardan duvara olan ısı transferi sürekli değiştiği için ayrıca
gazların özgül ısıları da sıcaklıkla değiştiği için ayrı bir n1 politrop üssü geçerli olur.
Süpürme sonu özellikleri (P1 ve T1) bilindiğine göre ε sıkıştırma oranına sahip bir
motorda politropik sıkıştırma sonunda sıkıştırma sonu basınç ve sıcaklığı;
P2 = P1ε n1
(5.19)
T2 = T1ε n1 −1
(5.20)
olur.
Sıkıştırma işleminin başlangıcında sıcak silindir duvarlarından daha soğuk olan
içerideki gazlara ısı geçişi olur. Sıkıştırma işleminin ortalarından sonra sıkıştırmanın
etkisiyle ısınmış olan gazlardan silindir duvarlarına ısı geçişi olur. Toplam olarak bu
içeri ve dışarı doğru olan ısı geçişlerinin birbirini dengelediği varsayılarak yaklaşık
olarak sıfır alınabilir. Bu durumda n1 politrop üssü için denklem;
36
(
)
A + BT1 ε n1 −1 + 1 =
R
n1 − 1
(5.21)
olur. Sıkıştırma işlemi boyunca silindir içinde benzin motorlarında çoğunlukla
havadan oluşan yakıt, artık egzoz gazları karışımı bulunur. Bu nedenle yaklaşık
hesaplarda A ve B katsayıları hava ile ilgili katsayılar olarak alınabilir. Böylece 5.21
numaralı denklemde bilinmeyen olarak yalnızca n1 politrop üssü yer alır. Bu
denklem üstel yapıda olduğu için analitik olarak çözülemez. Denklem sayısal bir
yöntemle örneğin Newton-Raphson yöntemiyle yaklaşık olarak çözülebilir. Benzin
motorlarında;
n1=1,32-1,39
(5.22)
T2=550-750 (K)
(5.23)
P2=10-14 (bar)
(5.24)
değerleri arasındadır.
5.3.3. Yanma işlemi
İçten yanmalı motorlarda en önemli işlem yakıtın ısı enerjisinin açığa çıktığı yanma
işlemidir. İçten yanmalı motorlarda klasik olarak genellikle ham petrolden üretilen
sıvı yakıtlar kullanılmakla birlikte değişik kaynaklı gaz yakıtlar veya başka sıvı
yakıtlar da kullanılabilmektedir.
Ham
petrolün
damıtılmasından
elde
edilen
sıvı
motor
yakıtları
değişik
hidrokarbonların farklı oranlardaki karışımından oluşur. Böyle bir karışımın
motorlarda değişken yüksek basınç ve sıcaklıklar altında havanın oksijeni ile
yanması boyunca birçok zincirleme kimyasal reaksiyon görülür. Ani basınç ve
sıcaklık artışları sonucu türbülanslı akım karışıkları olur. Ayrıca yanma odası
37
duvarlarından dışarıya ısı transferi olur. Bu arada silindir hacmi de değişir. Bütün bu
etkiler göz önüne alınarak motorlarda yanma olayını tam olarak modelleyip
hesaplamak oldukça güçtür.
Sıvı yakıtların yanması
İçten yanmalı motorlarda yanma hesaplarında kolaylık sağlamak amacı ile 1 kg
yakıtın veya 1 kmol yakıtın yanmasına göre düzenlemeler yapılabilir. Bu durumda
yanma denklemleri;
1 kg yakıt+Hava → Ürünler
(5.25)
1 kmol yakıt+Hava → Ürünler
(5.26)
şeklinde düzenlenebilir. Değişik hidrokarbonların karışımlarından oluşan sıvı
yakıtların yapısı ortalama olarak elemansal bileşim veya kapalı formül şeklinde
gösterilebilir.
Elemansal bileşimde 1 kg yakıtın analizi sonunda yapısında bulunan karbon,
hidrojen, oksijen, kükürt gibi elementlerin kütleleri ve su, kül gibi maddelerin
kütleleri belirlenerek c ' , h ' , o' , s ' , w' (su), a ' (kül) şeklinde gösterilir. Bu durumda;
c ' + h' + o ' + s ' + w' + a ' = 1 kg
(5.27)
olur. Elemansal bileşim biliniyorsa c ' kg karbonun, h' kg hidrojenin ve s ' kg
kükürdün yanması için gerekli olan oksijen miktarları ve yanma sonunda meydana
gelecek CO2, H2O ve SO2 miktarları kolayca hesaplanabilir. Böylece 1 kg yakıtın
yanması yaklaşık olarak incelenmiş olur. Burada yüksek sıcaklıklar altında yanma
sonucu meydana gelebilecek olan CO, C, H2, OH, CxHy ve NOx göz önüne alınmaz.
38
Kapalı formül ise yakıtın ortalama olarak 1 çeşit hidrokarbondan meydana geldiği ve
böyle bir ortalama yakıtın 1 kmol’ünün CcHhOoSsNn şeklinde gösterildiği
varsayımına dayanmaktadır. Buradaki c, h, o, s, n indisleri ortalama değerleri
gösterdiğinden tam sayılar olmayabilir ve 1kmol yakıtın yanması incelenirken
yüksek sıcaklıklar altında meydana gelebilecek olan;
CO2 ⇔ CO + 1 / 2O2
(5.28)
H 2O ⇔ OH + 1 / 2 H 2
(5.29)
N 2 + O2 ⇔ 2 NO
(5.30)
gibi çift yönlü birçok parçalanma reaksiyonları da göz önüne alınabilmekte ve
böylece ayrıntılı yanma ürünleri hesaplanabilmektedir.
Yakıtın elemansal bileşimi biliniyorsa basit şekilde orantılı olarak c ' karbonun
yanması için gerekli olan oksijen miktarı ve meydana gelebilecek olan CO2’nin
kilomol sayısı, ayrıca h' kg hidrojenin yanması için gerekli O2 miktarı ve meydana
gelebilecek olan su buharının kmol sayısı kolayca belirlenebilmektedir. Yakıtın
içinde hazır olarak bulunan o ' kg havanın oksijenine ek olarak yanmada kullanıldığı
düşünülür. Bu düşüncelerle ve yakıtın kükürt içermediği varsayılarak çözümlemeler
yapılabilmektedir. 1 kg yakıtı tam olarak yakmak için gerekli O2 miktarı;
⎤
⎡ 8c '
Omin = ⎢
+ 8h ' − o ' ⎥
⎦
⎣ 3
Omin
⎡ c ' h' o ' ⎤
=⎢ + − ⎥
⎣⎢12 4 32 ⎦⎥
⎛ kgO2 ⎞
⎜⎜
⎟⎟
⎝ kgy ⎠
(5.31)
⎛ kmolO2 ⎞
⎜⎜
⎟⎟
⎝ kgy ⎠
(5.32)
39
eşitlikleri ile bulunur. Havanın içerisinde normal koşullarda kütlesel olarak % 23
oksijen bulunmaktadır. Böylece 1 kg yakıtı tam yakabilmek için gerekli hava
miktarı;
hmin =
H min
⎤
Omin
1 ⎡ 8c '
=
+ 8h ' − o ' ⎥
⎢
0,23 0,23 ⎣ 3
⎦
'
Omin
1 ⎡ c ' h' o ⎤
=
=
⎢ + − ⎥
0,208 0,208 ⎣⎢12 4 32 ⎦⎥
⎛ kgh ⎞
⎜⎜
⎟⎟
⎝ kgy ⎠
(5.33)
⎛ kmolh ⎞
⎜⎜
⎟⎟
⎝ kgy ⎠
(5.34)
olur.
Hava fazlalık katsayısı
Benzinli motorlarda teorik olarak kullanılması gereken yakıt miktarından çoğunlukla
daha fazla yakıt kullanılır. Örneğin motorun tam güçte tam kapasitede çalışması
istendiğinde emilen havanın tümünün yanmada kullanılabilmesi ve hiç oksijen
artmaması için teorik olarak gerekenden fazla yakıt kullanılır. Bu durumda motor
tam güçte çalışır fakat hava ve oksijen yetersiz olduğundan tam yanma olmaz.
Yakıtın bir bölümü yanmadan dışarı atılır, motorun verimi düşer ve yakıt tüketimi
artar. 1kg yakıtı yakmak için gerçekte kullanılan hava miktarının, 1 kg yakıtı tam
yakmak için gerekli teorik hava miktarına oranına hava fazlalık katsayısı denir. İki
zamanlı benzinli motorlarda;
α = 0,80 − 0,96
(5.35)
aralığındadır.
Hava fazlalık katsayısı yanmayı etkileyen en önemli özelliktir. Bunun yanında
benzin ve dizel motorlarının yanma işlemleri birbirinden farklı özellikte olur. Yanma
işlemini ayrıca sıkıştırma oranı, silindir içindeki gazların basınç ve sıcaklıkları, devir
40
sayısı, silindir içindeki gaz hareketleri, yanma odasının şekli gibi birçok parametreler
de etkilemektedir. Benzin motorlarında yanmadan önce silindir içinde buharlaşmış
yakıt-hava karışımı bulunur. Ancak benzin kendi kendine kolay tutuşamadığı için
yanma olmaz. Ateşleme ve yanma bir buji tarafından başlatılır. Oluşan alev bir
küresel alev cephesi şeklinde belirli bir hızda yanma odasında ilerler. Belirli bir anda
alev cephesinin içerisinde yanmış gazlar, dışarısında yanmamış gazlar bulunur. Bu
arada piston hareket ettiği için silindir hacmi değişir. Alev cephesinin yüzeyi çeşitli
türbülans karışıklıkları nedeniyle çok düzgün olmaz. Alev cephesi tüm silindiri
kapladığında yanma tamamlanmış olur. Benzin motorlarında yanmanın çok hızlı
olduğu ve yanmanın başlangıcında yakıtın tümü silindir içinde bulunduğu için ayrıca
krank-biyel mekanizmasının yapısal özelliklerine bağlı olarak piston üst ölü nokta
civarında çok az hareket ettiğinden, basit hesaplarda benzin motorlarındaki yanmanın
sabit hacimde olduğu varsayılır.
Molekülsel değişim katsayısı
Kimyasal reaksiyonlarda kütle korunumu olmasına rağmen çoğunlukla kilomol
sayılarının toplamı sabit kalmaz. Yanma sonunda oluşan gazların kilomol sayısının
toplamının, yanma başlangıcındaki gazların kilomol sayısına oranına molekülsel
değişim katsayısı denir.
Yanma başlangıcı
Yanma sonu
:
M1 kmol taze karışım
:
Mr kmol artık egzoz gazı
:
M2 kmol yanmış karışım
:
Mr kmol artık egzoz gazı
Molekülsel değişim katsayısı için;
μ=
(M 2 + M r )
(M 1 + M r )
(5.36)
41
eşitliği yazılabilir. İki zamanlı benzin motorlarında molekülsel değişim katsayısı;
μ = (1,02 − 1,12)
(5.37)
aralığındadır.
Gaz karışımının özellikleri
Karışımın özelliklerini belirleyebilmek için, karışımı oluşturan karışanların
miktarlarını ve özelliklerini bilmek gerekir. Bir karışımda karışanların miktarları mol
olarak veya kütle olarak belirtilebilir. Karışımın kütlesi mk, karışanların kütlelerinin
toplamı; karışımın mol miktarı nk ise, karışanların mol miktarlarının toplamıdır.
Yani;
N
mk = ∑ mi
(5.38)
i =1
ve
N
nk = ∑ ni
(5.39)
i =1
olur. Karışanların kütlelerinin karışımın kütlesine oranı kütle oranı ( ymi ), karışanın
mol miktarının karışımın mol miktarına oranı ise mol oranı ( yni ) diye tanımlanır;
ymi =
ve
mi
mk
(5.40)
42
yn i =
ni
nk
(5.41)
olur. Bir maddenin kütlesi, maddenin mol miktarı ve mol kütlesi ile ifade edilebilir.
Bu durumda karışımın ortalama mol kütlesi;
M=
mk ∑ mi
=
=
nk
nk
∑n m = ∑ y
n
N
i
i
k
i =1
ni
Mi
(5.42)
olur. Karışımın ortalama gaz sabiti ise;
R=
R
M
(5.43)
şeklinde bulunur. Karışımın toplam iç enerjisi, entalpisi ve entropisi ise;
N
N
i =1
i =1
N
N
i =1
i =1
U = ∑U i = ∑ miui
H = ∑ H i = ∑ mi hi
N
N
i =1
i =1
S = ∑ Si = ∑ mi si
(5.44)
(5.45)
(5.46)
eşitlikleriyle bulunabilir [26].
Silindir içersindeki karşımın herhangi bir sıcaklıktaki ısıl özellikleri JANAF tabloları
kullanılarak belirlenebilir. Sıcaklığa bağlı olarak özgül ısı, oluşum entalpisi, Gibbs
serbest enerjisi, entropi ve denge sabiti değerleri bu tablolardan alınabilir. Ancak bu
tablolar simülasyon programlarında kullanılmaya elverişli olmadığından, bir grup
bileşenin özellikleri polinom şeklindeki eğrilere uygulanmış ve katsayıları
43
bulunmuştur. 3000-5000 K arasındaki değerler iki eğri ile belirlenmiştir. Her bir
bileşen için 300-1000 K ve 1000-5000 K arasındaki eğriler, 7’şer katsayıdan 14
katsayı ile verilmektedir [27].
−
C pi | R = ai1 + ai 2T + ai 3T 2 + ai 4T 3 + ai 5T 4
−
H i | RT = ai1 + ai 2T / 2 + ai 3T 2 / 3 + ai 4T 3 / 4 + ai 5T 4 / 5 + ai 6 / T
o
−
Si | R = ai1 ln T + ai 2T + ai 3T 2 / 2 + ai 4T 3 / 3 + ai 5T 4 / 4
o
(5.47)
(5.48)
(5.49)
Yanma ürünlerinin belirlenmesi
Benzin motorlarında tam gazda hava fazlalık katsayısı α = (0,80 − 0,96) ≺ 1 olur. Bu
durumda hava yetersiz olduğundan eksik yanma görülür. Yani yakıtın karbon ve
hidrojeninin tümü yanma için O2 bulamaz. Ayrıca benzin motorlarında yanma sonu
sıcaklıkları çok yüksek değerde olduğundan bazı yanma ürünleri parçalanarak yarı
yanmış veya yanmamış bileşiklere dönüşür.
Sıcaklık arttıkça parçalanma reaksiyonları da artar. Benzin motorlarında ayrıntılı
yanma hesaplarında tüm parçalanma reaksiyonları düşünülerek iteratif bir hesap
yöntemiyle ayrıntılı yanma ürünleri hesaplanabilir. Yanma sonu sıcaklığı arttıkça
yani parçalanma arttıkça CO, OH, H2, Cx, Hy gibi yarı yanmış veya yanmamış
maddelerin oranları da artar. Bunun sonucunda bu maddeler için kullanılması
gereken O2 yanmada kullanılamaz. Hava fazlalık katsayısı 1’den küçük olmasına
rağmen egzoz gazları içinde artmış O2 bulunabilir.
Burada yapılacak olan hesapta hava fazlalık katsayısının 1’den küçük olması
durumunda su gazı dengesinin oluştuğu ve yanma ürünleri içinde hiç O2 gazı
bulunamayacağı varsayılacaktır.
44
CO2 ⇔ CO + 1 / 2O2
H 2 + 1 / 2O2 ⇔ H 2O
(5.50)
CO2 + H 2 ⇔ CO + H 2O
KWG =
[YCO ]1 [YH O ]1
[Y ][Y ]
2
1
CO 2
1
(5.51)
H2
Burada;
kWG
: Su gazı denge katsayısı
YCO
: CO’nun hacimsel oranı
YH 2 O
: H2O’nun hacimsel oranı
YCO2
: CO2’nin hacimsel oranı
YH 2
: H2’nin hacimsel oranı
olarak tanımlanır. Su gazı dengesine göre yanma ürünlerinin CO2, CO, H2O, H2,
N2’den oluştuğu varsayılır ve seçilen yanma sonu sıcaklığına göre su gazı denge
katsayısı tablolardan okunur. Bu katsayıdan ve yanma eşitliğinden yararlanarak
yanma ürünlerinin kilomol sayıları ve hacimsel oranları hesaplanır ve benzer işlemler
iteratif olarak tekrarlanır.
Burada içten yanmalı motorlarda yapılan çeşitli deneylerden yararlanarak su gazı
denge katsayısı yerine;
kWG =
M H 2O
M CO
şeklinde bir katsayısı kullanılacaktır. Bu katsayı;
(5.52)
45
h'
= (0,17 − 0,19) ⇒ kWG = (0,45 − 0,50)
c'
(5.53)
h'
= 0,13 ⇒ kWG = 0,30
c'
(5.54)
değerlerini alır. Bu katsayıdan yararlanarak su gazı dengesine benzer yanma ürünleri
şu şekilde hesaplanabilir.
(1 − α )
⎫
H min ⎪
(1 + kWG )
⎪
⎪
⎪
'
c
⎪
M CO2 = − M CO
⎪
12
⎪
5
⎪⎪
M H 2 = kWG M CO
⎬M 2 = ∑ M i = M CO + ............. + M N 2
1
⎪
⎪
⎪
h'
M H 2O = − M H 2
⎪
12
⎪
⎪
⎪
M N 2 = 0,792αH min
⎪
⎪⎭
M CO = 0,416
(5.55)
46
M CO ⎫
M 2 ⎪⎪
⎪
⎪
M CO2 ⎪
YCO2 =
M2 ⎪
⎪
⎪
M H 2 ⎪⎪ 5
YH 2 =
⎬∑ Yi = 1,000
M2 ⎪ 1
⎪
⎪
M H 2O ⎪
YH 2 O =
M2 ⎪
⎪
⎪
M N 2 ⎪⎪
YN 2 =
M 2 ⎪⎭
YCO =
(5.56)
5
Ag = ∑ Yi Ai
(5.57)
i =1
5
Bg = ∑ Yi Bi
(5.58)
i =1
Burada Ai ve Bi çeşitli gazların belirli sıcaklık aralıklarındaki özgül ısılarıdır. İçten
yanmalı motorlarda yanma olayı (1500–2800) K sıcaklıklarında gerçekleştiği için bu
sıcaklık aralıklarındaki özgül ısılar kullanılmalıdır. Çeşitli gazların (0–1500) K ve
(1500–2800) K aralıklarındaki özgül ısıları Çizelge 5.1’de verilmiştir.
Çizelge 5.1. Bazı gazların lineer özgül ısı değişimindeki A ve B katsayıları [28]
Gaz
0–1500 ° C aralığında
A
B
19,880
0,002638
1500–2800 ° C aralığında
A
B
21,991
0,001449
Oksijen
19,663
0,004641
23,300
0,001550
Azot
19,716
0,002500
21,553
0,001457
Hidrojen
20,628
0,000206
19,198
0,001758
Hava
47
Çizelge 5.1. (Devam) Bazı gazların lineer özgül ısı değişimindeki A ve B katsayıları
CO
19,868
0,002670
22,100
0,001430
CO2
22,754
0,19000
38,209
0,003349
Su buharı
23,490
0,005359
25,458
0,004438
Yakıtın alt ısıl değeri
Bir yakıtın 1 kg veya 1 kmol’ünün kayıpsız yanması sonunda açığa çıkan ısı
miktarına ısıl değer denir. Üst ısıl değer ve alt ısıl değer olmak üzere iki ısıl kavram
kullanılmaktadır.
İçten yanmalı motorlarda yanma sonu sıcaklıkları yüksek olduğundan yanma
sonunda oluşacak su buhar fazında olur ve suyun buharlaşma ısısından
yararlanılamaz. Bu nedenle içten yanmalı motorlardaki yanma hesaplarında alt ısıl
değer kullanılmaktadır.
Isıl değer pratik olarak yakıtın elemansal bileşimine bağlı olarak deneylerden elde
edilmiş amprik bağıntılardan belirlenebilir. Mendeleyev eşitliğinden;
H u = 33,91c ' + 125,6h ' − 10,89(o ' − s ' ) − 2,51(9h ' + w)
(kJ/kg)
(5.59)
ile bulunur. Benzin motorlarında α ≺ 1 hava fazlalık katsayısı ile yanmada eksik
yanma nedeni ile alt ısıl değerin tümünden yararlanılamaz.
H u' = H u − ΔH u
(kJ/kg)
(5.60)
olur. Burada eksik yanma ile oluşacak ısı kaybı,
ΔH u ≅ 114(1 − α ) H min
(kJ/kg)
(5.61)
48
eşitliği ile bulunur.
Yanmanın termodinamik denklemi
Burada 1 kg yakıtın yanması düşünülerek 2-3 noktaları arasında termodinamiğin 1.
kanunundan yararlanılarak sıcaklıkla ilgili bir bağıntı elde edilecektir. Benzin
motorlarında yanmanın termodinamik denklemi;
ξ z H u'
+ ( A + BT2 )T2 = μ (Ag + BgT3 )T3
M 1 (1 + γ r )
(5.62)
olur. Burada λ basınç artma oranı uygun şekilde seçilirse bilinmeyen olarak yalnızca
T3 yanma sonu sıcaklığı kalır. Denklem T3’e göre düzenlenirse;
aT32 + bT3 + c = 0
(5.63)
şeklinde 2. derece bir denklem elde edilir. Bu denklemin + kökü bize yanma sonu
sıcaklığını verir. Öyleyse;
− b + b 2 − 4ac
T3 =
2a
(5.64)
olur. Yanma sonu basıncı ise;
P3 = λP2
(5.65)
bağıntısıyla elde edilir. Burada λ basınç artma oranıdır.
Benzin motorlarında;
T3=2400–2900 (K)
(5.66)
49
P3=40-60 (bar)
(5.67)
aralığındadır.
5.3.4. Genişleme işlemi
Genişleme işlemi boyunca gerçekte çevre ile sürekli ısı alış verişi olur ( dQ ≠ 0 ).
Genişleme boyunca başlangıçta çok sıcak olan gazlardan duvarlara, sonlara doğruda
duvarlardan gazlara doğru ısı geçişi olabilir. Yani politropik genişleme boyunca n2
politrop üssü sürekli olarak değişir. Bu noktada duyarlı hesaplarda genişlemenin
adım adım incelenmesi ve zincirleme olarak her adımda geçerli olan politrop
üssünün belirlenmesi gerekir. Burada yapılacak hesaplarda genişleme boyunca
ortalama bir n2 politrop üssünün geçerli olduğu varsayılacaktır.
n2 politropik üssü 3–4 noktaları arasında Termodinamiğin 1. Kanunu yazılarak elde
edilecek bir üstel denklemin çözümü sonunda bulunabilir.
Ag + BgT3 (1 + ε 1− n2 ) =
R
n2 − 1
(5.68)
Bu denklemin deneme yanılma yoluyla veya bir sayısal yöntemle çözümü sonunda n2
ortalama genişleme politrop üssü hesaplanabilir. Öyleyse genişleme işlemi sonu
özellikleri için;
P4 =
T4 =
P3
εn
(5.69)
2
T3
εn
2
−1
bağıntıları yazılabilir. Benzin motorlarında;
(5.70)
50
n2=1,23-1,30
(5.71)
P4=3,5-6 (bar)
(5.72)
T4=1200-1700 (K)
(5.73)
aralığındadır.
5.3.5. Egzoz işlemi
Gerçekte genişleme işleminin sonlarına doğru egzoz portu açılma avansı kadar önce
egzoz portu açılır ve yanmış gazlar kendi basınçlarının etkisiyle hızla egzoz
kanalından dışarıya boşalmaya başlar. Silindirin içindeki gazların basıncı bir
kanaldan boşalma olduğu için hızlı bir şekilde düşer. Bir kanalda gazların boşalması
ile ilgili termodinamik bağıntılardan yararlanarak basınç ve sıcaklık arasında;
Tr =
T
b
k hava
k hava −1
Pb
Pr
(5.74)
eşitliği yazılabilir. Burada;
khava: Hava için izentropik üs (1,4)
(5.75)
Çevrim hesabının başlangıcında artık egzoz gazları basıncı Pr ve egzoz gazları
sıcaklığı Tr seçilmiştir. Seçilmiş olan bu değerlere bağlı olarak artık egzoz gazları
sıcaklığı Tr (5.74) bağıntısından hesaplanır. Eğer son hesaplanan değer ile başta
seçilen değer arasındaki fark % 2-3’ten küçükse hesabın tutarlı olduğu varsayılır.
Eğer fark oranı fazla çıkarsa Pr ve Tr yeniden seçilerek çevrim hesabının
tekrarlanması gerekir.
51
5.4. Motor Performans Karakteristikleri
Taşıt motorları geniş bir devir sayısı aralığında çalıştırılabilirler. Minimum devir
sayısı, motorun kararlı çalıştırılabilmesi için gerekli şartlar yani benzin motorlarında
hava-yakıt karışımının oluşması ve emilmesi, maksimum devir sayısı ise, emme ve
egzoz işlemlerinin verimi, parçaların ısıl gerilimleri, artan atalet kuvvetleri, mekanik
verimdeki düşme v.b. tarafından sınırlandırılmaktadır [29].
Bir motorun en avantajlı çalışma durumları; maksimum güç (Pemax), maksimum
moment (Memax) ve en az özgül yakıt tüketimi (bemin)’i sağladığı durumlardır. Bu
çalışma durumları, motorun kullanım amacı ve yaptığın işin özellikleri tarafından
belirlenir [29].
Bir taşıt motorunun fonksiyonu, motorun efektif gücünün, hareket direncine
(tüketilen ve genellikle yolun özelliklerine ve hıza bağlı olarak değişmekte olan güç)
eşitlik şartları tarafından belirlenir. Tüketilen güç yalnız taşıt hızına değil, aynı
zamanda yolun durumu, yük ve ivme gibi faktörlere de bağımlı olduğuna göre,
motorun çalışma şartları kararlı değildir. Çünkü motora gelen yük sürekli
değişmektedir. Hareket direncinin kısa süreli artışları, hızla giden taşıtın kinetik
enerjisinin bir kısmı tarafından, uzun süreli yüksek dirençler ise, motor momenti
tarafından karşılanır. Motor momenti, gaz pedalının motora daha fazla yakıt
gönderecek yönde hareket ettirilmesiyle artırılır. Bu nedenle motorun çalışma analizi,
sadece birkaç çalışma durumunun değil, değişik çalışma durumlarının araştırılmasına
yönelik olmalıdır [29].
Motorun değişik çalışma koşullarına göre değişim gösteren ve motor performans
karakteristikleri diye adlandırılan parametreler mevcuttur. Bu parametreler içten
yanmalı motorlar için şu şekilde sıralanır:
•
Ortalama indike ve efektif basınç (Pmi, Pme)
52
•
İndike ve efektif güç (Ni, Ne)
•
İndike ve efektif moment (Mi, Me)
•
İndike ve efektif ısıl verim (η i ,ηe )
•
Hacimsel verim (ηv )
•
İndike ve efektif özgül yakıt tüketimi (bi, be)
5.4.1. Ortalama indike ve efektif basınçlar
İçten yanmalı motorlarda güç hesaplaması yapılırken yanma sonunda meydana gelen
en yüksek basınç dikkate alınmaz. Çünkü bu basınç iş zamanında hacim büyümesi
sonucunda hızla düşer. Bu nedenle motor gücünün hesaplanmasında ortalama indike
basınç kullanılır. Benzin motorlarında teorik ortalama indike basınç, çevrim hesabı
sonuçlarını kullanarak;
Pmi' =
1 ⎞
1 ⎛
1 ⎞⎤
P1ε n1 ⎡ λ ⎛
⎜1 − n2 −1 ⎟ −
⎜1 − n1 −1 ⎟⎥
⎢
ε − 1 ⎣ n2 − 1 ⎝ ε
⎠ n1 − 1 ⎝ ε
⎠⎦
(5.76)
bağıntısından elde edilebilir. İndikatör diyagramının köşelerinin gerçek çevrimde
yuvarlatılması nedeniyle, gerçek ortalama indike basınç teorik değerden biraz daha
küçük olur. Bu durumda gerçek ortalama indike basınç;
Pmi = ϕi Pmi'
(5.77)
olur. Burada ϕi indikatör diyagramı yuvarlatma katsayısıdır ve benzin motorlarında;
ϕi =0,94-0,97
(5.78)
53
aralığındadır. Mekanik kayıplara harcanan iş ve pompalama işi bir Pmm mekanik
kayıplar ortalama basıncı şeklinde hesaba katılır ve;
Pmm = a + bV p
(5.79)
bağıntısından bulunabilir. Burada Vp ortalama piston hızıdır ve;
Vp =
Hn
30
(5.80)
eşitliğiyle bulunur. Çeşitli motor tiplerine bağlı olarak değişen a ve b katsayıları ise
çizelge 5.2’de verilmiştir.
Çizelge 5.2. Mekanik kayıplar ortalama basıncındaki a ve b katsayıları [30]
Motor tipi
Benzin Motorları
Dizel Motorları
z ≤ 6, H/D 1
a
0,049
b
0,0152
z ≤ 8, H/D ≺ 1
0,039
0,0132
z ≤ 6, H/D ≺ 1
0,034
0,0113
Açık yanma odalı
0,089
0,0118
Ön yanma odalı
Girdaplı yanma
0,103
0,089
0,0153
0,0135
odalı
Ortalama efektif basınç, silindir içindeki gazların çevrim işine karşılık gelen ortalama
indike basınçtan Pmi, mekanik kayıplar ortalama basıncının Pmm çıkarılması ile elde
edilir. Yani;
Pme = Pmi − Pmm
(5.81)
54
olur.
5.4.2. İndike ve efektif güçler
Silindir içerisinde oluşan basıncın piston üzerine etkilediği güç indike güçtür ve z
silindirli bir motorun indike gücü için;
Ni =
Pmi zVh n
k 60
(5.82)
bağıntısı yazılabilir. Burada,
Pmi
: Ortalama indike basınç, (bar)
z
: Silindir sayısı
Vh
: Strok hacmi, (m3)
n
: Motor hızı, (1/min)
k
: Bir devirde iş yapan kurs sayısı, (iki zamanlı motorlar:1)
Volandan elde edilen güç efektif güç olarak tanımlanır. Piston krank mekanizması
tarafından üretilen indike güç, hareketli parçaların sürtünmesi ve pompalama
kayıplarından doğan bir kısım güç düşüşleri sonucunda volandan azalmış şekilde
elde edilir. z silindirli bir motorun efektif gücü için;
Ne =
Pme zVh n
k 60
bağıntısı yazılabilir.
5.4.3. İndike ve efektif momentler
İndike moment için indike güce bağlı olarak;
(5.83)
55
Mi =
1000 N i
ω
(5.84)
bağıntısı yazılabilir. Burada ω açısal hızı ifade eder ve;
ω=
πn
(5.85)
30
eşitliği ile elde edilir. Benzer şekilde efektif moment için de efektif güce bağlı
olarak;
Me =
1000 N e
ω
(5.86)
eşitliği yazılabilir.
5.4.4. İndike ve efektif ısıl verimler
İndike verim, silindir içinde bir çevrim sonunda elde edilen indike işin, bu işi elde
etmek için harcanan yakıt ısısına oranıdır. Öyleyse;
ηi =
Wi
Q
(5.87)
yazılabilir. Bazı düzenlemeler sonunda indike verim için;
ηi =
Pmi M 1RT5
H u P5ηv
eşitliği yazılabilir. Burada;
(5.88)
56
Pmi
: Ortalama indike basınç, (bar)
M1
: 1 kg yakıt için kullanılan taze gaz
R
: Gaz sabiti, (0,287 kJ/kgK)
T5
: Süpürme karışımı sıcaklığı, (K)
Hu
: Yakıtın alt ısıl değeri, (kJ/kg)
P5
: Süpürme karışımı basıncı, (bar)
ηv
: Hacimsel verim, (%)
olarak tanımlanır. Benzer şekilde efektif verim için de;
ηe =
Pme M 1RT5
H u P5ηv
(5.89)
eşitliği yazılabilir.
5.4.5. İndike ve efektif özgül yakıt tüketimleri
Motorlarda tüketilen yakıt miktarının verimle ters orantılı olacağı tahmin edilebilir.
Ayrıca yakıt tüketimi zaman ile orantılıdır. Motorları karşılaştırabilmek için birim
zamanda (1 saniyede veya 1 saatte) tüketilen yakıt miktarını karşılaştırmak veya
kullanmak daha gerçekçi olur. Ancak doğal olarak küçük bir motor birim zamanda az
yakıt, büyük bir motor ise fazla yakıt tüketir. Böylece birim zamanda tüketilen yakıt
miktarı da motorların sağlıklı bir şekilde karşılaştırılmasında yeterli olmaz. Bunun
yerine birim zamanda (1 saatte) birim güç (1 kW) için tüketilen yakıt miktarı
kullanılır ve özgül yakıt tüketimi (be) diye adlandırılır. 1 saatte tüketilen yakıt
miktarına toplam yakıt tüketimi (Be) denir. Öyleyse;
B =
my
t
⎛ kg ⎞
⎜ ⎟
⎝ h ⎠
(5.90)
57
be =
B
Ne
⎛ kg ⎞
⎟
⎜
⎝ kWh ⎠
(5.91)
şeklinde ifade edilebilir. Efektif verim ile özgül yakıt tüketimi arasında ise;
be =
3600
H uηe
(5.92)
bağıntısı geçerlidir. Burada;
Hu
: Yakıtın alt ısıl değeri, (kJ/kg)
ηe
: Efektif verim, (%)
Benzer şekilde indike özgül yakıt tüketimi içinde;
bi =
3600
H uηi
(5.93)
eşitliği yazılabilir.
Bir motorun çevrim hesaplarını değişik devirlerde benzer şekilde yapabiliriz.
Minimum ve maksimum devir aralığında seçilen devirlerde çevrim hesapları
tamamlanarak motorun tam gazda değişik devirlerdeki güç, moment, özgül yakıt
tüketimi ve verim değerleri bu şekilde bulunduktan sonra devir sayısına göre motor
hız karakteristikleri çizilebilir.
Yukarıda açıklanan işlemler motorun tam gazda nominal devirde çalışmasına karşı
gelmektedir. Motorun efektif güç, moment, efektif verim gibi karakteristiklerinin
devir sayısı ile değişimlerini belirlemek için çevrim hesaplarının farklı devirlerde
tekrarlanması gerekir. Pratik hesap amacı ile bazı amprik bağıntıları kullanarak
58
nominal devirdeki değerlerden diğer devirlerdeki değerler bulunabilir. Herhangi bir
nx devrindeki özellikler;
x=
nx
nN
(5.94)
N e , x = N e , N x(1 + x − x 2 )
(5.95)
N e , x1000
wx
(5.96)
M e, x =
wx =
πnx
30
be , x = be , N (1,2 − 1,2 x + x 2 )
ηe, x =
3600
H u be, x
şeklinde belirlenebilir [31].
(5.97)
(5.98)
(5.99)
59
6. SİMÜLASYON SONUÇLARI VE TARTIŞMA
Bu bölümde, önceki bölümlerde incelenen çevrim simülasyonunun termodinamiksel
modeline göre hazırlanan simülasyon programından elde edilen sonuçlar
bulunmaktadır. Simülasyon programının değişken parametrelere karşı duyarlılığı ve
gerçek motor test sonuçları ile uyuşması, programın hassasiyeti ve kabul edilebilirliği
açısından da çok önemlidir. Bu bölümde ayrıca bazı firmaların ürettikleri iki zamanlı
benzinli motorların test sonuçlarıyla, aynı motorların simülasyon sonuçları
karşılaştırılmıştır. Hazırlanan simülasyon programında, silindir basınç-sıcaklık
eğrileri ile değişik sıkıştırma oranları ve hava fazlalık katsayılarına göre motor
performans eğrileri elde edilmiştir. Simülasyonu yapılan motorun özellikleri Çizelge
6.1’de verilmiştir.
Çizelge 6.1. Simülasyonu yapılan motorun karakteristikleri
Parametre
Değer
Silindir çapı (m)
0,097
Strok (m)
0,074
Sıkıştırma oranı
6-10
Motor hızı (1/min)
1000-4000
EGAA ( ο KMA) AÖN’dan önce
60
EMAA ( ο KMA) AÖN’dan önce
40
EGKG ( ο KMA) AÖN’dan sonra
60
ο
EMKG ( KMA) AÖN’dan sonra
40
60
Çizelge 6.2. Simülasyonda yapılan bazı kabuller
Parametre
Değer
P0 (Atmosfer basıncı)
1 (bar)
T0 (Atmosfer sıcaklığı)
293 (K)
P5 (Süpürme basıncı)
1,3 (bar)
Peg (Egzoz sistemi karşı basıncı)
0,06 (bar)
Tr (Artık egzoz gazları sıcaklığı)
1100 (K)
γr (Artık egzoz gazları katsayısı)
0,25
β2+ζ (Kısılma ve sürtünme kayıpları)
2,8
ρ (Havanın yoğunluğu)
1,2 (kg/m3)
k (bir devirde iş yapan kurs sayısı)
1
Simülasyon işleminde 6’dan 10’a kadar sıkıştırma oranının 2’şer birim adımla ve
0,80’den 0,96 ‘ya kadar hava fazlalık katsayısının 0,8’er birim adımla değişimleri,
motor hızının 1000 1/min’den 4000 1/min’e kadar 500 1/min’lik adım değişimleri
hesaplanmıştır. Öncelikli olarak motor hızı 3000 1/min’de, sıkıştırma oranı 10’da ve
hava fazlalık katsayısı 0,96’da sabit tutularak motorun genel karakteristik eğrileri ve
daha sonrada sıkıştırma oranının ve hava fazlalık katsayısının bazı motor
karakteristik eğrilerine etkileri sırasıyla incelenmiştir.
6.1. Silindir Basınç, Sıcaklık ve Motor Karakteristik Eğrileri
Silindir içerisindeki basınç değişimi silindir hacmine ve krank mili açısına göre
incelenmiştir. Şekil 6.1’de silindir basıncının silindir hacmine göre değişimi ve Şekil
6.2’de silindir basıncının krank mili açısına göre değişimi görülmektedir.
61
Şekil 6.1. Silindir basıncının silindir hacmiyle değişimi
Şekil 6.2. Silindir basıncının krank mili açısıyla değişimi
Şekil 6.1 ve Şekil 6.2’de maksimum silindir basıncı 46,97 bar değerini almıştır.
Benzin motorlarında maksimum silindir basıncı 35–75 bar değerleri arasındadır.
62
Şekil 6.3. Gaz sıcaklığının krank mili açısıyla değişimi
Silindir gaz sıcaklığının krank mili açısına göre değişimi Şekil 6.3’de görülmektedir.
Yanma ile birlikte sıcaklıktaki hızlı artışı görebilmek mümkündür. Silindir içinde
sıkıştırma sonu sıcaklığı 724 K ve maksimum gaz sıcaklığı 2454 K değerini almıştır.
Şekil 6.4. Ortalama indike ve efektif basıncın motor hızına bağlı değişimi
Maksimum ortalama efektif basınç 1800 1/min’de 11 bar ve maksimum ortalama
indike basınç 2200 1/min’de 11,58 bar olarak belirlenmiştir (Şekil 6.4).
63
Şekil 6.5. Ortalama indike ve efektif momentin motor hızına bağlı değişimi
Motor momenti silindirdeki ortalama basıncın bir fonksiyonu olduğundan indike ve
efektif moment eğrileri ortalama indike ve efektif basınç eğrileriyle aynı paralellikte
seyretmektedir. Maksimum efektif moment 1800 1/min’de 74,83 Nm ve maksimum
indike moment 2000 1/min’de 78,78 Nm değerini almıştır (Şekil 6.5).
Şekil 6.6. Ortalama indike ve efektif gücün motor hızına bağlı değişimi
Maksimum efektif motor gücü 3800 1/min’de 40,79 kW ve maksimum indike motor
gücü 3800 1/min’de 44,91 kW değerini almıştır (Şekil 6.6).
64
Tanaka firmasının 2002 yılında ürettiği iki zamanlı Benzinli TC-2501 modeline ait
bazı motor özellikleri Çizelge 6.2’de ve motor hızına bağlı moment ve güç grafikleri
Şekil 6.7’de görülmektedir.
Çizelge 6.3. Motor özellikleri [32]
Silindir çapı (m)
0,034
Strok (m)
0,027
Sıkıştırma oranı
7,2:1
Maksimum güç (kW)
0,889
Maksimum tork (Nm)
1,287
Maksimum devir (1/min)
11000
65
Şekil 6.7. Motor gücü ve momentinin motor hızına bağlı değişimi [32]
Şekil 6.8. Motor gücü ve momentinin motor hızına bağlı değişimi
Şekil 6.7’de görüldüğü gibi TC-2501’in maksimum motor gücü 7500 1/min’de 0,889
kW ve maksimum motor momenti 5500 1/min’de 1,287 Nm’dir.
Aynı motorun simülasyon programıyla elde edilen motor gücü-motor hızı ve motor
momenti-motor hızı grafiği Şekil 6.8’de görülmektedir.
66
Motor özellikleri simülasyon programına girildiğinde maksimum motor gücü 7500
1/min’de 0,8862 kW ve maksimum motor momenti 5500 1/min’de 1,285 Nm olarak
belirlenmiştir. Sonuçlar motorun firmasınca verilen spesifikasyonlarla uyuşmaktadır.
ROTAX firmasının 2000 yılında ürettiği iki zamanlı benzinli 277UL modeline ait
bazı motor özellikleri Çizelge 6.3’de ve motor hızına bağlı güç ve moment grafikleri
sırasıyla Şekil 6.9 ve Şekil 6.11’de görülmektedir.
Çizelge 6.4. Motor özellikleri [33]
Silindir çapı (m)
0,072
Strok (m)
0,066
Sıkıştırma oranı
6,7:1
Maksimum güç (kW)
19,852
Maksimum tork (Nm)
30,821
Maksimum devir (1/min)
7000
Şekil 6.9. Motor gücü-motor hızı grafiği [33]
67
Şekil 6.10. Motor gücü-motor hızı grafiği
Şekil 6.11. Motor momenti-motor hızı grafiği [33]
68
Şekil 6.12. Motor momenti-motor hızı grafiği
Şekil 6.9’dan görüldüğü gibi 227UL’nin maksimum motor gücü 6000 1/min’de
19,852 kW ve Şekil 6.11’de görüldüğü gibi maksimum motor momenti 5500
1/min’de 30,821 Nm değerini almıştır.
Aynı motorun simülasyon programıyla elde edilen motor gücü-motor hızı ve motor
momenti-motor hızı grafikleri sırasıyla Şekil 6.10 ve Şekil 6.12’te görülmektedir.
Motor özellikleri simülasyon programına girildiğinde maksimum motor gücü 6000
1/min’de 19,852 kW ve maksimum motor momenti 5500 1/min’de 30,821 Nm olarak
belirlenmiştir. Sonuçlar motorun firmasınca verilen spesifikasyonlarla uyuşmaktadır.
69
Şekil 6.13. Ortalama indike ve efektif özgül yakıt tüketiminin motor hızına bağlı
değişimi
Özgül yakıt tüketiminin motor hızına bağlı değişimi Şekil 6.13’de görülmektedir.
Motor hızının artmasıyla birlikte silindir içerisinde oluşan ısı kayıpları azalmakta ve
böylece yakıttan elde edilebilir güç artmaktadır. Motor hızının artışı ile özgül yakıt
tüketiminde bir miktar düşüş görülmesine karşın yüksek motor hızlarında özgül yakıt
tüketiminde yükselme görülmektedir. Minimum efektif özgül yakıt tüketimi 2800
1/min’de 0,3003 kg/kWh ve minimum indike özgül yakıt tüketimi 2800 1/min’de
0,2939 kg/kWh değerini almıştır.
70
Şekil 6.14. Ortalama indike ve efektif verimin motor hızına bağlı değişimi
Maksimum efektif verim 2400 1/min’de % 46,86 ve maksimum indike verim de
2600 1/min’de % 53,62 değerini almıştır (Şekil 6.14).
6.2. Sıkıştırma Oranının Etkisi
Sıkıştırma oranının silindir basıncı ve gaz sıcaklığına ve motor performans
karakteristiklerine etkisi 3000 1/min, HFK:0,96 ve üç farklı sıkıştırma oranı (6:1-8:110:1) için incelenmiştir.
71
Şekil 6.15. Sıkıştırma oranının silindir basıncına etkisi
Şekil 6.16. Sıkıştırma oranının silindir basıncına etkisi
72
Şekil 6.17. Sıkıştırma oranının gaz sıcaklığına etkisi
Sıkıştırma oranı artışıyla birlikte silindir basıncı ve gaz sıcaklığında yükselme
görülmektedir. Maksimum silindir basıncı, sıkıştırma oranı 6:1 olduğunda 28,58 bar
ve sıkıştırma oranı 10:1’e çıktığında 46,97 bar olmaktadır (Şekil 6.15 ve Şekil 6.16).
Maksimum gaz sıcaklığı ise sıkıştırma oranı 6:1 iken 2378 K ve sıkıştırma oranı 10:1
olduğunda 2454 K değerini almıştır (Şekil 6.17).
Şekil 6.18. Sıkıştırma oranının ortalama efektif basınca etkisi
Maksimum silindir basıncının artışıyla ortalama efektif basınç da artış görülmektedir.
Maksimum ortalama efektif basınç sıkıştırma oranı 6:1 için 1800 1/min’de 8,48 bar
73
ve sıkıştırma oranı 10:1 için 1900 1/min’de için 11,58 bar değerini almıştır (Şekil
6.18).
Şekil 6.19. Sıkıştırma oranının efektif momente etkisi
Efektif momentin değişimi de ortalama efektif basıncın değişimine paraleldir.
Maksimum efektif moment sıkıştırma oranı 6:1 için 1900 1/min’de 54,89 Nm ve
sıkıştırma oranı 10:1 için 2000 1/min’de 74,83 Nm değerini almıştır (Şekil 6.19).
Şekil 6.20. Sıkıştırma oranının efektif güce etkisi
74
Sıkıştırma oranının artışıyla efektif güçte de artış görülmüştür. Sıkıştırma oranı 6:1
için maksimum efektif güç 3800 1/min’de 29,46 kW ve sıkıştırma oranı 10:1 için
3800 1/min’de 40,79 kW değerini almıştır.
Şekil 6.21. Sıkıştırma oranının efektif özgül yakıt tüketimine etkisi
Sıkıştırma oranının artışı ile birlikte güçte görülen artış efektif özgül yakıt
tüketiminde düşüş olarak hissedilir. Efektif özgül yakıt tüketimi sıkıştırma oranı 6:1
için 2600 1/min’de 0,4352 kg/kWh ve sıkıştırma oranı 10:1 için 2700 1/min’de
0,2939 kg/kWh değerini almıştır (Şekil 6.21).
75
Şekil 6.22. Sıkıştırma oranının efektif verime etkisi
Sıkıştırma oranının artışıyla efektif verim 6:1 için 2400 1/min’de % 31,7 ve
sıkıştırma oranı 10:1 için 2500 1/min’de % 46,86 değerini almıştır (Şekil 6.22).
6.3. Hava Fazlalık Katsayısının Etkisi
Hava fazlalık katsayısının silindir basıncı ve gaz sıcaklığına ve motor performans
karakteristiklerine etkisi, 3000 1/min, sıkıştırma oranı 10:1 ve üç farklı hava fazlalık
katsayısı (0,85-0,90-0,96) için incelenmiştir.
76
Şekil 6.23. Hava fazlalık katsayısının silindir basıncına etkisi
Şekil 6.24. Hava fazlalık katsayısının silindir basıncına etkisi
Hava fazlalık katsayısının 0,85’ten 0,96’ya artışı sonrasında maksimum silindir
basıncı 46,97 bar’dan 46,83 bar’a düşmüştür (Şekil 6.23 ve Şekil 6.24).
77
Şekil 6.25. Hava fazlalık katsayısının gaz sıcaklığına etkisi
Hava fazlalık katsayısının artışıyla gaz sıcaklığındaki değişim daha belirgindir. Hava
fazlalık katsayısı 0,85 için maksimum gaz sıcaklığı 3168 K ve hava fazlalık katsayısı
0,96 için maksimum gaz sıcaklığı 2454 K değerini almıştır (Şekil 6.25).
Şekil 6.26. Hava fazlalık katsayısının ortalama efektif basınca etkisi
78
Ortalama efektif basıncın maksimum değeri, 0,85 hava fazlalık katsayısı değeri için
1900 1/min’de 11,71 bar ve 0,96 hava fazlalık katsayısı değeri için 1900 1/min’de
11,58 bar olarak hesaplanmıştır (Şekil 6.26).
Şekil 6.27. Hava fazlalık katsayısının efektif momente etkisi
Maksimum efektif moment 0,85 hava fazlalık katsayısı değeri için 2300 1/min’de
74,83 Nm ve 0,96 hava fazlalık katsayısı değeri için 2300 1/min’de 75,1 Nm değerini
almıştır (Şekil 6.27).
Şekil 6.28. Hava fazlalık katsayısının efektif güce etkisi
79
Maksimum efektif motor gücü 0,85 hava fazlalık katsayısı değeri için 3800 1/min’de
41,26 kW ve 0,96 hava fazlalık katsayısı değeri için 3800 1/min’de 40,79 kW
değerini almıştır (Şekil 6.28).
Şekil 6.29. Hava fazlalık katsayısının efektif özgül yakıt tüketimine etkisi
Minimum efektif özgül yakıt tüketimi 0,85 hava fazlalık katsayısı değeri için 2700
1/min’de 0,3282 kg/kWh ve 0,96 hava fazlalık katsayısı değeri için 2700 1/min’de
0,2939 kg/kWh değerini almıştır (Şekil 6.29).
Şekil 6.30. Hava fazlalık katsayısının efektif verime etkisi
80
Hava fazlalık katsayısı arttıkça efektif verimde artış görülmektedir. Maksimum
efektif verim 0,85 hava fazlalık katsayısı değeri için 2800 1/min’de % 36,81 ve 0,96
hava fazlalık katsayısı değeri için 2700 1/min’de % 46,86 değerini almıştır (Şekil
6.30).
81
7. SONUÇ VE ÖNERİLER
Bu çalışmada, iki zamanlı benzinli bir motorun performansının bilgisayar yardımı ile
analizini incelemek üzere matematiksel bir simülasyon modeli geliştirilmiştir.
MATLAB/SIMULINK programlama dilinde yazılmış bir bilgisayar programı
yardımıyla sıkıştırma oranı, motor hızı ve hava fazlalık katsayısı için motorun krank
mili açısına bağlı olarak silindir basınç ve sıcaklık değişimleri elde edilerek ortalama
indike ve efektif basınç, indike ve efektif moment, indike ve efektif güç, indike ve
efektif özgül yakıt tüketimi ve indike ve efektif ısıl verim gibi bazı motor performans
parametreleri hesaplanmıştır.
Çevrim işlemlerinin her biri 1°’lik KMA değişimlerinde ve değişik parametreler için
hesaplanmış ve hesaplamalar sonucunda silindir basınç ve sıcaklık ve motor
performans parametreleri için grafikler çizdirilmiştir. Bu grafiklerden yararlanarak
silindir basıncının ve gaz sıcaklığının değişimleri, sıkıştırma oranının ve hava
fazlalık katsayısının motor performansına etkileri incelenmiştir.
Hazırlanan bilgisayar programı farklı motor hızları, sıkıştırma oranları ve hava
fazlalık katsayıları için çalıştırıldığında;
1. Sıkıştırma oranının artmasıyla sıkıştırma sonu ve maksimum silindir basınç ve
sıcaklıkları artmaktadır. Maksimum silindir basıncının artmasıyla ortalama indike ve
efektif basınç, indike ve efektif moment, indike ve efektif güç ve indike ve efektif ısıl
verim gibi parametrelerde artış görülmektedir. İndike ve efektif özgül yakıt tüketimi
ise azalmakta ve daha da ekonomikleşmektedir.
2. Sabit sıkıştırma oranında artan hava fazlalık katsayısı ile maksimum silindir basınç
ve sıcaklıklarında, ortalama indike ve efektif basınç, indike ve efektif moment,
indike ve efektif güç ve özgül yakıt tüketiminde azalma görülmüştür. Karışım
fakirleştikçe ideal gaz özelliklerine yaklaştığından indike ve efektif ısıl verimde artış
görülmüştür.
82
3. Artan motor hızı ile ortalama indike ve efektif basınç, indike ve efektif moment,
indike ve efektif güç gibi parametrele artmaktadır.
Öneriler;
1. Matematiksel model geliştirilirken emisyonlarla ilgili bir değerlendirme
yapılmamıştır. Matematiksel model içerisine emisyon modellerinin eklenmesi
sonuçları daha gerçekçi hale getirecektir.
2. Süpürme ve egzoz işlemlerinin simülasyonu, portların açılma ve kapanma açıları
da dikkate alınarak geliştirilebilir.
3. Matematiksel model geliştirilirken silindir duvar sıcaklığı sabit değer olarak kabul
edilmiştir. Gerçek bir motorda bu değer her an değişmektedir. Daha gerçekçi bir
model için bu değişim dikkate alınabilir.
83
KAYNAKLAR
1. Sekmen, Y., Erduranlı, P., Koca, A., “Buji ile ateşlemeli bir motorun ideal
hava-yakıt çevrim analizi ile performans hesabı”, G.Ü. Fen Bilimleri Dergisi,
18(1): 103-114 (2005).
2. Öztürk, E., “İki zamanlı direkt püskürtmeli bir dizel motorunun bilgisayar
yardımı ile performans analizi”, Yüksek Lisans Tezi, Gazi Üniversitesi Fen
Bilimleri Enstitüsü, Ankara, 1-10 (2003).
3. Çetinkaya, S., “Dört zamanlı buji ile ateşlemeli bir motor performansının
bilgisayar yardımı ile simülasyonu” , Doktora Tezi, Gazi Üniversitesi Fen
Bilimleri Enstitüsü, Ankara, 1-3 (1987).
4. Durgun, O., “İçten yanmalı motorlar ders notları”, Karadeniz Teknik
Üniversitesi Mühendislik Fakültesi, Trabzon, 1-3(2008).
5. Okur, M., “İki zamanlı ve iki silindirli bir model uçak motorunun tasarımı ve
imali”, Yüksek Lisans Tezi, Gazi Üniversitesi Fen Bilimleri Enstitüsü,
Ankara, 3-13 (2001).
6. Wyczalek, F. A., “Two-stroke engine technology in 1990’s”, SAE Paper,
No:910663, 1-3, (1991).
7. Ohyagi, S., Harigaya, Y., Kakizaki, K., Toda, F., “Estimation of flame
propagation in spark- ignition engine by using turbulent burning model”
Saitama University, 503-510 (1985).
8. Befrui, B., Kratochwill, H., “Multidimensional calculation of combustion in a
loop-scavenged two-stroke cycle engine” , İnternational Symposium
Comodia 90, 465-474 (1990).
9. Kuo, P., S., “Cylinder pressure in a spark ignition engine: a computational
model”, Journal of Undergraduate Sciences, 3:141-145 (1996).
10. Yıldız, E., Arslan, S., Aybek, A., “Bir benzin motoru çevrim analizinin
matematiksel modellemesi”, Mühendislik ve Makine, 45(535): 35-45 (2000).
11. Moriyoshi, Y., Kikuchi, K., Morikawa, K., Takimoto, H., “Numerical
analysis of mixture preparation in a reverse uniflow–type two-stroke gasoline
engine”, Elsevier Science B.V., 18-26 (2001).
12. Sekmen, Y., Erduranlı, P., Koca, A., “Buji ile ateşlemeli bir motorun ideal
hava-yakıt çevrim analizi ile performans hesabı”, G.Ü. Fen Bilimleri Dergisi,
18(1): 103-114 (2005).
84
13. Mitianiec, W., Forma, M., COMODIA 9O, “Mixture formation at spray
guided direct injection in SI two-stroke engine”, Czasopismo Techniczne,
Austria, 115-127 (2008).
14. Mikalsen, R., Roskilly, A. P., “The design and simulation of a two-stroke
free-piston compression ignition engine for electrical power generation”,
Applied Thermal Engineering, 28 (2008): 589-600 (2007).
15. Sekmen, P., Sekmen Y., “Mathematical modeling of SI engine cycle with
actual air-fuel cycle analyses” , Mathematical and computational
applications, 12(3): 161-171 (2007).
16. Semin, N., Rosli, A., Bakar, R., “In-cylinder flow through piston-port engines
modeling using dynamic mesh”, Journal of applied sciences research, 4(1):
58-64 (2008).
17. Motoyama, Y., Gotoh, T., “The effect of higher compression ratio in two
stroke engines”, SAE paper, No:931512, 355-362 (1990).
18. Safgönül, B., “Pistonlu Motorlar Cilt 1”, İTÜ Makine Fakültesi ve Ofset
Atölyesi, İstanbul, 89-106 (1989).
19. Sürmen, A., Karamangil, M. İ., “Motor Termodinamiği”, Alfa Akademi, 79105 (2004).
20. Küçükşahin, F., “Gemi Makineleri, Cilt 3”, Güven Kitap Kırtasiye, İstanbul,
309-428 (2000).
21. Küçükşahin, F., “Gemi Makineleri Operasyonu-2, Cilt 2”, Birsen Yayınevi,
İstanbul, 27-34 (1998).
22. Durgun, O., “Motor termodinamiği ders notları”, Karadeniz Teknik
Üniversitesi Mühendislik Fakültesi, Trabzon, 7-10, 18-20 (2008).
23. Çetinkaya, S., “Motor Dinamiği”, Nobel Yayın Dağıtım, Ankara, 6-10
(1999).
24. Blair, G., P., “Design and Simulation of Two-Stroke Engines R-161”, SAE,
Warrendale, 1-412 (1996).
25. Safgönül, B., Arslan, H.E., Ergeman, M., Soruşbay C., “İçten Yanmalı
Motorlar, Cilt 2”, Birsen Yayınevi, İstanbul, 77-80 (1999).
26. Çengel,Y., A., Boles, M., A., “Mühendislik Yaklaşımıyla Termodinamik, Cilt
2”, Taner Derbentli, Mc Graw Hill, 600-617 (1996).
85
27. Borat, O., Sürmen, A., Balcı, M., “İçten Yanmalı motorlar, Cilt 1”, Birsen
Yayınevi, İstanbul, 75-77 (1992).
28. Çomaklı, K., Yüksel, B., Şahin, B., Karagöz, Ş., “Kazan bacalarında
meydana gelen enerji ve ekserji kayıpları”, Tesisat Mühendisliği Dergisi, 92:
12-16 (2006).
29. Çetinkaya, S., “Taşıt Mekaniği”, Nobel Yayın Dağıtım, Ankara, 22-23
(1999).
30. Durgun, O., “Motor çevrimlerinin hesabı için pratik bir yöntem”, Mühendis
ve Makine, 32(383): 19-28 (1991).
31. Kolchin, A., Demidov, V., “Design Of a Automotive Engines”, Mır
Publishers, Moscow, 116-123 (1984).
32. İnternet : ROTAX “Engine Specifications” http://www.rotax.com/en/ (2000).
33. İnternet : TANAKA “Engine Specifications” http://tanaka.com.tr/ (2002).
86
EKLER
87
EK-1 Simülasyon Program Kodları
clear;
clc;
sira=1;
prompt={'Silindir Çapi (m): ','Zaman (m) :','Sıkıştırma
oranı:','Hava fazlalık katsayısı:'};
dlg_title='Girdiler : ';
num_lines=1;
def={'x.xxx','x.xxx','xx','x.xx'};
sor1=inputdlg(prompt,dlg_title,num_lines,def);
D=str2num(sor1{1});
H=str2num(sor1{2});
SO=str2num(sor1{3});
alfa=str2num(sor1{4});
%girdiler
% D=0.097;
% SO=10;
% H=0.074;
L=0.1;
alfa=0.96;
z=1;
k=1;
P0=1;
T0=293;
P5=1.2;
n=1.5;
Peg=0.06;
dT=20;
Tr=1000;
Gr=0.20;
BKareEps=4;
Vm=130;
ro=1.2;
fis=0.25;
fied=1.10;
A=19.880; B=0.002638; R=8.314;
for devir=0:100:4000;
devirler(sira)=devir;
maxdevir=3000;
%hacimler
%zaman hacmi
Vh=pi*D^2/4*H;
%ölü hacim
Vc=Vh/(SO-1);
%piston AÖN^da iken silindir hacmi
Va=Vh+Vc;
%piston yolu
88
EK-1. (Devam) Simülasyon Program Kodları
r=H/2;
landa2=r/L;
rp=D/2;
Apis=pi*rp^2;
%S=r*(1-cosQ)+L*(1-sqrt(1-landa2^2*sin^2Q))
%5,6 noktasındaki hacim
QEAA=140;
QEAArad=pi*QEAA/180;
S5=r*(1-(cos(QEAArad)))+L*(1-sqrt(1landa2^2*(sin(QEAArad))*(sin(QEAArad))));
V5=S5*Apis+Vc;
V6=S5*Apis+Vc;
%1,4 noktasındaki hacim
QEGAA=120;
QEGAArad=pi*QEGAA/180;
S1=r*(1-(cos(QEGAArad)))+L*(1-sqrt(1landa2^2*(sin(QEGAArad))*(sin(QEGAArad))));
V1=S1*Apis+Vc;
V4=S1*Apis+Vc;
%ateşleme avansı A.Ö.N^dan sonra 340 KMA
AA=340;
AArad=pi*AA/180;
S2=r*(1-(cos(AArad)))+L*(1-sqrt(1landa2^2*(sin(AArad))*(sin(AArad))));
V2=S2*Apis+Vc;
%3 noktasındaki hacim
Q3=345;
Q3rad=pi*Q3/180;
S3=r*(1-(cos(Q3rad)))+L*(1-sqrt(1landa2^2*(sin(Q3rad))*(sin(Q3rad))));
V3=S3*Apis+Vc;
%süpürme
Pr=1.18*P5
Pa=0.95*P5
Ta=T0*(Pa/P0)^((n-1)/n)
dPa=BKareEps * ((Vm*devir)/(devir))^2 * ro/2 * 10^(-6);
P1=P5-dPa
T1=(Ta+dT+fis*Gr*Tr)/(1+Gr)
VerVol=SO/(SO-1)*P1/P5*Ta/(Ta+dT+Gr*Tr)*fied
%sıkıştırma
%newton-rpson
fark=0.000001; epsilon=0.00001; maxiter=10; x0=1.4;
f=A+B*T1*(SO^(x0-1)+1)-R/(x0-1);
for say=1:maxiter
y=B*T1/SO*log(SO)*SO^x0+R/((x0-1)^2);
if abs(y)<0.0001
disp('türev sıfıra çok yakın'
89
EK-1. (Devam) Simülasyon Program Kodları
break, end
kok=x0-(A+B*T1*(SO^(x0-1)+1)-R/(x0-1))/y;
hata=abs(kok-x0);
hatatek=2*hata/(abs(kok)+fark);
x0=kok;
w=A+B*T1*(SO^(x0-1)+1)-R/(x0-1);
if (hata<fark)|(hatatek<fark)|(abs(w)<epsilon)
break, end
end
if say==maxiter
disp('max adım aşıldı')
break, end;
n1=x0
%sıkıştırma sonu basınç, sıcaklık
P2=P1*(V1/V2)^n1
T2=T1*(SO)^(n1-1)
%yanma işlemi
ksu=0.50;
Oy=0;
My=6.999*12.011+17.462*1.008;
c=6.999*12.011/101.667;
h=17.462*1.008/101.667;
h/c
Hmin=1/0.208*(c/12+h/4+Oy/32);
hmin=1/0.230*(8*c/3+8*h);
M1=alfa*Hmin;
m1=alfa*hmin;
Hu=33.91*c+125.6*h-2.51*9*h;
%yanma ürünleri
Mco=0.416*((1-alfa)/(1+ksu))*Hmin;
Mco2=c/12-Mco;
Mh2=ksu*Mco;
Mh2o=h/2-Mh2;
MN2=0.792*alfa*Hmin;
M2=Mco+Mco2+Mh2+Mh2o+MN2;
%yanma ürünlerinin hacimsel oranları
rco=Mco/M2;
rco2=Mco2/M2;
rh2=Mh2/M2;
rh2o=Mh2o/M2;
rN2=MN2/M2;
%yanma gazlarının ortalama özgül ısısı
Ag=rco*22.100+rco2*38.209+rh2*19.198+rh2o*25.458+rN2*21.553;
Bg=rco*0.001430+rco2*0.003349+rh2*0.001758+rh2o*0.004438+rN2*0.00145
7;
%yanma denklemi
Hu=45864;
dHu=114*(1-alfa)*Hmin*1000;
90
EK-1. (Devam) Simülasyon Program Kodları
Hug=Hu-dHu;
fiz=0.875;
lamda=4;
%molekülsel değişim katsayısı
M0=M2/M1;
M=(M0+Gr)/(1+Gr);
%yanma denklemi
%((fiz*Hug)/(M1*(1+Gr))+((A+B*T2)*T2))=M*(Ag+Bg*T3)*T3
a=M*Bg;
b=M*Ag;
c=((fiz*Hug)/(M1*(1+Gr))+((A+B*T2)*T2));
T3=(-b+(sqrt(b^2+4*a*c)))/(2*a)
P3=lamda*P2
%Genişleme işlemi
%newton-rophson
fark=0.000001; epsilon=0.00001; maxiter=10; X0=1.3;
f=Ag+Bg*T3*(SO^(1-X0)+1)-R/(X0-1);
for say=1:maxiter
y=-Bg*T2*log(SO)*1/(SO^(X0-1))+R/((X0-1)^2);
if abs(y)<0.0001
disp('türev sıfıra çok yakın')
break, end
kok=X0-(Ag+Bg*T3*(SO^(1-X0)+1)-R/(X0-1))/y;
hata=abs(kok-X0);
hatatek=2*hata/(abs(kok)+fark);
X0=kok;
w=Ag+Bg*T3*(SO^(1-X0)+1)-R/(X0-1);
if (hata<fark)|(hatatek<fark)|(abs(w)<epsilon)
break, end
end
if say==maxiter
disp('max adım aşıldı')
break, end;
n2=X0
%Yanma sonu basıncı ve sıcaklığı
P4=P3/((V1/V2)^n2)
T4=T3/(SO^(n2-1))
Trg=T4/((P4/Pr)^(1/3))
T5=T4/(SO^(n2-1))
%motor karakteristikleri
%ortalama indike basınç
fii=0.94;
pmi=P1*SO^n1/(SO-1)*[lamda/(n2-1)*(1-1/(SO^(n2-1)))-1/(n1-1)*(11/(SO^(n1-1)))]
Pmi=fii*pmi;
%ortalama efektif basınç
Vpm=H*devir/30;
Pmm=0.039+0.0132*Vpm*10;
91
EK-1. (Devam) Simülasyon Program Kodları
Pme=Pmi-Pmm;
%efektif güç
Ne=Pme*z*100*Vh*devir/(k*60);
x=devir/maxdevir
%indike güç
Ni=Pmi*100*Vh*devir/(k*60);
%efektif özgül yakıt tüketimi ve efektif verim
Rr=0.287;
Veref=Pme*m1*Rr*Ta/(Hug*P5*VerVol);
be=3600/(Hug*Veref);
%yakıt tüketimi
Ge=Ne*be;
%mekanik ve indike verim
VerMek=(Pmi-Pmm)/Pmi;
Verin=Veref/VerMek;
%indike özgül yakıt tüketimi
bi=3600/(Hug*Verin);
%efektif moment ve indike moment
W=pi*devir/30;
Me=1000*Ne/W;
Mi=1000*Ni/W;
sira=sira+1;
end
%pv diyagram 1-2; bölgesi bölgesi
V12=V1:-0.0000001:V2;
say1=1;
for say2=V1:-0.0000001:V2;
P12(say1)=(V1/V12(say1))^n1*P1;
say1=say1+1;
end
say1=say1-1;
%pv diyagramı 2-3 bölgesi
V23(1)=V2
V23(2)=V3
P23(1)=P12(say1)
P23(2)=0.85*lamda*P12(say1);
%pv diyagram 3-4 bölgesi bölgesi
P3=P23(2);
V34=V3:0.0000001:V4;
say3=0;
92
EK-1. (Devam) Simülasyon Program Kodları
for say4=V3:0.0000001:V4
say3=say3+1;
P34(say3)=(V3/V34(say3))^n2*P3;
end
P34(1)=P23(2)
%pv diyagram 4-5 bölgesi bölgesi
V45(1)=V4;
V45(2)=V5;
P45(1)=P34(say3);
P45(2)=(P1+Pa)/2;
%pv diyagram 1-a bölgesi bölgesi
V1a(1)=V1;
V1a(2)=Va
P1a(1)=P1;
P1a(2)=Pa;
figure(1);
plot(V12,P12,'black',V23,P23,'black',V34,P34,'black',V45,P45,'black'
,V1a,P1a,'black');
%krank mili açısı-silindir basıncı diyagramı
%1-2 bölgesi
Q11=-180*pi/180;
Q22=-5*pi/180;
Q111=90*pi/180;
Q12=Q11:0.0001:Q22;
say5=0;
for say6=Q11:0.0001:Q22;
say5=say5+1;
P121(say5)=(((r*(1-(cos(Q111)))+L*(1-sqrt(1landa2^2*(sin(Q111))*(sin(Q111)))))*Apis+Vc)/((r*(1(cos(Q12(say5))))+L*(1-sqrt(1landa2^2*(sin(Q12(say5)))*(sin(Q12(say5))))))*Apis+Vc))^n1*P1;
end
%2-3 bölgesi
Q23(1)=Q12(say5);
q3=10;
q3rad=q3*pi/180;
Q23(2)=q3rad;
P123(1)=P121(say5);
P123(2)=P3;
%3-4 bölgesi
Q33=10*pi/180;
Q44=80*pi/180;
Q333=10*pi/180;
Q34=Q33:0.0001:Q44;
say7=0;
for say8=Q33:0.0001:Q44;
93
EK-1. (Devam) Simülasyon Program Kodları
say7=say7+1;
P134(1)=P123(2);
P134(say7)=P3/(((r*(1-(cos(Q34(say7))))+L*(1-sqrt(1landa2^2*(sin(Q34(say7)))*(sin(Q34(say7))))))*Apis+Vc)/((r*(1(cos(Q333)))+L*(1-sqrt(1landa2^2*(sin(Q333))*(sin(Q333)))))*Apis+Vc))^(n2);
end
%4-5 bölgesi
Q55=80*pi/180;
Q66=180*pi/180;
Q555=-84*pi/180;
Q45=Q55:0.0001:Q66;
say9=0;
for say10=Q55:0.0001:Q66;
say9=say9+1;
P145(1)=P134(say7);
P145(say9)=P4/(((r*(1-(cos(Q45(say9))))+L*(1-sqrt(1landa2^2*(sin(Q45(say9)))*(sin(Q45(say9))))))*Apis+Vc)/((r*(1(cos(Q555)))+L*(1-sqrt(1landa2^2*(sin(Q555))*(sin(Q555)))))*Apis+Vc))^(n2);
end
figure(2);
plot(Q12*180/pi,P121,'black',Q23*180/pi,P123,'black',Q34*180/pi,P134
,'black',Q45*180/pi,P145,'black');
%krank mili açısı-gaz sıcaklığı diyagramı
Q11_=-180*pi/180;
Q22_=-5*pi/180;
Q111=-180*pi/180;
Q12_=Q11_:0.001:Q22_;
say5=0;
for say6=Q11_:0.001:Q22_;
say5=say5+1;
T121(say5)=(((r*(1-(cos(Q111)))+L*(1-sqrt(1landa2^2*(sin(Q111))*(sin(Q111)))))*Apis+Vc)/((r*(1(cos(Q12_(say5))))+L*(1-sqrt(1landa2^2*(sin(Q12_(say5)))*(sin(Q12_(say5))))))*Apis+Vc))^(n1-1)*T1;
end
%2-3 bölgesi
Q23_(1)=Q12_(say5);
q3=10;
q3rad=q3*pi/180;
Q23_(2)=q3rad;
T123(1)=T121(say5);
T123(2)=T3;
%3-4 bölgesi
Q33_=10*pi/180;
94
EK-1. (Devam) Simülasyon Program Kodları
Q44_=180*pi/180;
Q333=-10*pi/180;
Q34_=Q33_:0.001:Q44_;
say7=0;
for say8=Q33_:0.001:Q44_;
say7=say7+1;
T134(1)=T123(2);
T134(say7)=T3/(((r*(1-(cos(Q34_(say7))))+L*(1-sqrt(1landa2^2*(sin(Q34_(say7)))*(sin(Q34_(say7))))))*Apis+Vc)/((r*(1(cos(Q333)))+L*(1-sqrt(1landa2^2*(sin(Q333))*(sin(Q333)))))*Apis+Vc))^(n2-1);
end
%4-5 bölgesi
Q55_=180*pi/180;
Q66_=360*pi/180;
Q555=10*pi/180;
Q45_=Q55_:0.001:Q66_;
say9=0;
for say10=Q55_:0.001:Q66_;
say9=say9+1;
T145(1)=T134(say7);
T145(say9)=T4/(((r*(1+(cos(Q45_(say9))))+L*(1sqrt(1+landa2^2*(sin(Q45_(say9)))*(sin(Q45_(say9))))))*Apis+Vc)/((r*(1-(cos(Q555)))+L*(1-sqrt(1landa2^2*(sin(Q555))*(sin(Q555)))))*Apis+Vc))^(n2-1);
end
figure(3);
plot(Q12_*90/pi,T121,'black',Q23_*90/pi,T123,'black',Q34_*90/pi,T134
,'black',Q45_*90/pi,T145,'black');
%Motor karakteristikleri grafikleri
figure(4);
plot(Mex,'black-');
hold on;
plot(Mix,'black--');
legend('Me','Mi');
figure(5);
plot(Nex,'black-');
hold on;
plot(Nix,'black--');
legend('Ne','Ni');
figure(6);
plot(bex,'black-');
hold on;
plot(bix,'black--');
legend('be','bi');
figure(7);
plot(Pmex,'black-');
95
EK-1. (Devam) Simülasyon Program Kodları
hold on;
plot(Pmix,'black--');
legend('Pme','Pmi');
figure(8);
plot(Verefx,'black-');
hold on;
plot(Verinx,'black--');
legend('Efektif Verim','İndike Verim');
96
ÖZGEÇMİŞ
Kişisel Bilgiler
Soyadı, adı
:KAYA, Göksel
Uyruğu
: T.C.
Doğum tarihi ve yeri
: 17.08.1981 Ordu
Medeni hali
: Bekar
Telefon
: 0 (452) 233 48 65
Faks
: 0 (452) 233 52 30
e-mail
: [email protected]
Eğitim
Derece
Eğitim Birimi
Yüksek lisans
Gazi Üniversitesi / Makine Eğitimi Böl.
Lisans
Gazi Üniversitesi/ Makine Eğitimi Böl.
Lise
Anadolu Denizcilik Meslek Lisesi
Yabancı Dil
İngilizce
Hobiler
Masa Tenisi, Satranç