IS FUNCTION

EM 316 Matematiksel İktisat II
K. Lopcu
ÇÜ, Ekonometri
BÖLÜM 6
DİNAMİK ANALİZE GİRİŞ: DURAĞAN-DURUM DENGE ve DURAĞAN
ENFLASYON
Durağan Durum: Durağan durum analizinde bazı değişkenlerin sabit bir büyüme hızında
büyüdüğü varsayılır. Diğer bir deyişle, değişkenler zaman içerisinde değişmeyen bir
oranda değişim gösterirler.
x değişkeni için sürekli zamanda büyüme oranı =
d ln xt 1 dx

dt
x dt
(1)
ve x değişkeninin t ve t-1’inci dönemler arasındaki büyüme oranı;
x t  x t 1
.
x t 1
Yukarıda denklem (1)'deki büyüme oranının kesikli zaman karşılığı
 ln xt  ln xt  ln xt 1 = ln
xt
x t 1
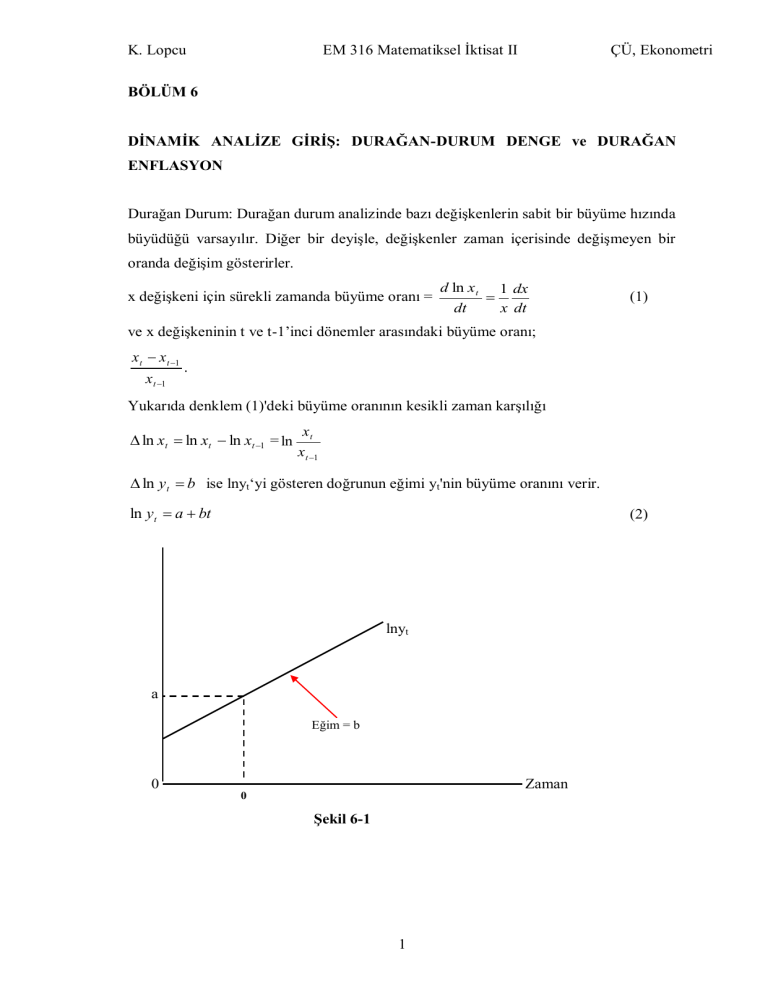
 ln y t  b ise lnyt‘yi gösteren doğrunun eğimi yt'nin büyüme oranını verir.
ln y t  a  bt
(2)
lnyt
a
Eğim = b
0
Zaman
0
Şekil 6-1
1
K. Lopcu
EM 316 Matematiksel İktisat II
ÇÜ, Ekonometri
DURAĞAN DURUM İÇİN VARSAYIM
Durağan durumda, değişkenlerin değişme oranı sabit ama sıfırdan farklı olacağı için,
bireylerin fiyatlar genel seviyesindeki (ve diğer değişkenlerdeki) bu sabit değişme
oranını fark etmemeleri veya gelecek dönemlerde bu değişimin devam edeceğini doğru
olarak öngörmemeleri mümkün değildir. Fiyatlar genel düzeyindeki bu değişimin fark
edilmesi ve beklenmesi durağan durum analizinin doğal bir varsayımıdır.
Enflasyonun söz konusu olduğu bir ortamda reel ve nominal faiz oranları farklılık
gösterecektir.
1+Rt = (1+rt).(1+ πt) = 1+rt + πt+ rt.πt
Burada rt reel faiz oranı, Rt nominal faiz oranı ve t: t ve t+1 dönemleri arasında
beklenen enflasyon oranıdır. Enflasyon ve reel faizin düşük olduğu ekonomilerde son
terim sıfır civarında olacaktır. Dolayısıyla, nominal ve reel faiz arasındaki ilişki şu
şekilde basitleştirilebilir.
Rt  rt   t
(6)
Durağan durumda enflasyon oranının sıfırdan farklı olmakla birlikte sabit bir değer
alacağının altını çizmek gerekir.
KLASİK MODELDE ENFLASYON
Nüfusta bir artışın ve teknolojik ilerlemenin olmadığı, Klasik bir ekonomide, parasal
otoritenin para stokunu bir dönemden diğerine  oranında artırdığını varsayalım. Bu
durumda fiyat düzeyi Pt'de bir dönemden diğerine  oranında bir artış gösterecektir.
 ln M t  
(7)
  ln M t  ln M t 1
Mt: t dönemindeki para stoğu.
2
EM 316 Matematiksel İktisat II
K. Lopcu
ÇÜ, Ekonometri
: Para arzının büyüme hızı. Pozitif.
lnPt
lnMt
Eğim = 
Zaman
Şekil 6-2
IS ve LM
yt  c ( yt  T , rt )  I ( yt , rt )  G
Yukarıdaki mal piyasası denge koşulu rt için çözüldüğünde IS fonksiyonunu verecektir.
rt   ( yt , T , G),
 y t  0,
 T  0,
G  0
(9)
Notasyonu basitleştirmek için G ve T'nin sabit olduğu varsayıldığında,
rt   ( y t ) yazılabilir.
(9.a)
(9.a) nolu ifadeyi (6) nolu ifadede yerine yazarsak, IS fonksiyonu
Rt  ( yt )   t
(10)
şeklinde elde edilir.
Enflasyonun söz konusu ise para talebi, gelir yanında, reel değil nominal faizin oranının
bir fonksiyonu olacaktır. Niçin?
M tD
 L( y t , Rt ),
Pt
M tD  M tS  M t ,
3
EM 316 Matematiksel İktisat II
K. Lopcu
ÇÜ, Ekonometri
Mt
 L ( y t , Rt )
Pt
Mt
Pt
Reel Para Balansı,  ln Pt   ln M t    
Yukarıdaki düzenleme ve tanımlamalar ışığında LM fonksiyonu, nominal faiz oranını,
gelir düzeyini, fiyatlar genel düzeyi ve para stokunun bir fonksiyonu olarak elde
edilebilir.
Grafiksel olarak, IS ve LM fonksiyonlarının yeni durumu Şekil 6.3'te
gösterilmiştir.
R
t
A
 Mt 
 Pt 
 
t
(yt)+t
LM
(yt)
yt
Şekil 6-3
Klasik modelde, emek piyasası dengede ve çıktı düzeyi de tam istihdam çıktı düzeyine
eşit olduğu için, IS ve LM eğrilerinin kesişme noktasındaki çıktı düzeyi tam istihdam
çıktı düzeyine eşit olmak durumundadır. Bu durum Şekil 6.4'te özetlenmiştir. Şekil
6.4'te durağan durum dengesinde para arzı ve fiyatlar genel düzeyinin aynı oranda
büyüdüğüne dikkat ediniz.
4
K. Lopcu
EM 316 Matematiksel İktisat II
ÇÜ, Ekonometri
R
t
M 
P
 
R ----------------------------------------
=
r ----------------------------------------
(yt)+t
(yt)
y*
yt
Şekil 6-4
KARŞILAŞTIRMALI DURAĞAN DURUM
Parasal otorite para arzının büyüme hızını arttırdığında, enflasyonda aynı oranda artacak
ve IS eğrisi enflasyondaki artış kadar yukarı kayacaktır.
Ancak, yukarı kayan IS
eğrisinin, başlangıçtaki LM eğrisi ile kesiştiği nokta yeni durağan durum (D-D) dengesi
olamaz. Çünkü bu noktada çıktı doğal çıktı düzeyinin üzerindedir. Yeni D-D dengede
çıktı tam istihdam çıktı düzeyine eşit olmak durumundadır. Bu da, ancak, LM eğrisinin
sola kayması ile mümkündür. Fakat LM eğrisinin sola kayması, fiyatlar genel düzeyinin
ya sıçraması, ya da bir müddet para arzının büyüme hızından daha hızlı büyümesi ile
mümkündür. Sonuç olarak, para arzının büyüme hızındaki artış, yeni D-D dengesinde
reel balansların daha düşük bir düzeyde gerçekleşmesine yol açacaktır. Bu durum, Şekil
6.5 ve 6.6'da grafiksel olarak gösterilmiştir. Özetlemek gerekirse,

Para arzındaki artış oranı (1-0)
ne kadar yüksekse, enflasyondaki (π1-π0) ve
nominal faiz oranındaki (R1-R0) artış da o kadar yüksek olur.
5
K. Lopcu
EM 316 Matematiksel İktisat II
R
ÇÜ, Ekonometri
1
 
M
P
M  0
P
 
0=0
1=1
1>0
R1
R0
0
(y)+1
r
1
(y)+0
(y)
y
y*
Şekil 6-5

Bununla beraber bu durumda, ekonomik aktörler tarafından tutulan reel para
1
0
M  M 
balansı daha düşük düzeyde gerçekleşecektir. Yani,      olacaktır.
P P

Farklı D-D denge noktalarında değişkenler (M ve P) farklı değerler alabilirler.
Ancak belirli bir D-D dengede M ve P’nin zaman içerisindeki büyüme hızları
sabit ve birbirine eşit olacaktır.

Bir D-D denge noktasından başka bir D-D dengesine geçerken, fiyatlar genel
düzeyi t*'da sıçramak yerine yeni D-D denge noktasına tedricen (yavaş yavaş)
ulaşıyorsa, geçiş dönemi boyunca enflasyon oranı para arzının büyüme hızını
aşacaktır. Başka bir ifade ile geçiş dönemi boyunca  ln Pt   ln M t , yani   
olacaktır.

Para arzının büyüme hızındaki artış, reel faiz de dahil, M/P dışında hiç bir reel
değişken üzerinde etkili olmayacaktır. Bu durum paranın süper yansızlığı olarak
ifade edilir.

Bunun anlamı M/P dışındaki tüm reel büyüklüklerin enflasyon oranından
bağımsız olduğudur. (,,M/P, r ).
6
EM 316 Matematiksel İktisat II
K. Lopcu
ÇÜ, Ekonometri
lnPt
lnMt
Eğim=1
Eğim=0
Zaman
t*
Şekil 6-6
REEL BALANS ETKİSİ
Yukarıdaki analizlerde ortaya çıkan Klasik Modelde “Paranın Süper Yansızlığı”
sonucu, hane halkı tüketiminin reel servetten etkilenmesi durumunda ortadan
kalkacaktır. Tüketimin reel servetten ve onun bir bileşeni olan reel balanslardan (M/P)
etkilenmesi durumunda tüketim fonksiyonu,
C = c(Yt -T, rt, Mt/Pt ),
0<C1<1,
C2<0,
C3<0 şeklinde yazılabilir.
Bu durumda denklem (9.a)’da verilen IS fonksiyonu yerine,
rt   ( yt ,

Mt
),
Pt
1  0 ,  2  0 yazılabilir.
Reel balansların tüketim ve dolayısıyla IS fonksiyonu içinde yer alması, Klasik
Modelde paranın süper yansızlığını sona erdirecektir. Para arzının büyüme
hızının ve bunun sonucu olarak enflasyon oranının artması reel balansları
düşüreceğinden, tüketim azalacak, IS eğrisi sola kayacak ve neticede reel faiz
oranı düşecektir(,,M/P,IS sola kayar, r ). Paranın süper yansızlığının,
reel balans etkisi (M/P) nedeni ile artık geçerli olmayacağı Şekil 6.7’de grafiksel
olarak gösterilmektedir.
7
K. Lopcu
EM 316 Matematiksel İktisat II
R
ÇÜ, Ekonometri
1
 
M
P
0
M 
P
 
R1
R0
0
0
(Y,(M/P)0)+1
(Y,(M/P)1)+1
1
r
r1
1
(Y,(M/P)0)+0
(Y,(M/P)0)
(Y,(M/P)1)
Y
Şekil 6-7
ENFLASYONUN REFAH MALİYETİ
Şimdiye kadar beklenen enflasyonun kişi başına düşen gelir, tüketim ve reel faiz oranı
gibi çoğu reel büyüklük üzerinde çok az etkisi olduğunu gördük. Reel balans etkisini ve
büyümeyi göz ardı edersek, yukarıda bahsedilen değişkenlerin hiçbirisi enflasyon
artışından etkilenmeyecektir. O halde, enflasyonun toplumdaki bireylerin refahı
üzerinde bir etkisi olup olmadığını sormak yerinde olacaktır.
Ancak, enflasyonun sosyal refah üzerinde olumsuz bir etkisi söz konusudur. Bu etki
enflasyon sebebiyle, görece daha düşük düzeyde gerçekleşen reel balanslar aracılığıyla
ve “taban aşındırma maliyeti” üzerinden toplumdaki tüketicilerin daha düşük bir fayda
düzeyine ulaşmalarına neden olacaktır. Bunun nedeni, belli bir harcama (gelir)
düzeyinde, daha düşük reel balanslarla ekonomideki mal ve hizmet değişiminin
("alışveriş") gerçekleşmesi için, daha çok zaman ve enerji harcamak zorunluluğudur.
Dinlenmek ve eğlenmek için daha fazla "boş" zaman bireylerce arzu edildiğine göre,
daha yüksek durağan (sabit) enflasyon oranları toplumun bireyleri için daha düşük
fayda düzeylerine yol açacaktır.
8
K. Lopcu
EM 316 Matematiksel İktisat II
ÇÜ, Ekonometri
Enflasyonun refah maliyeti mikro iktisattaki "tüketici artığı" kavramı kullanılarak
hesaplanabilir. Herhangi bir malın tüketiminden elde edilen toplam fayda, tüketilen
miktara kadar o malın talep eğrisi altında kalan alan hesaplanarak bulunabilir. Malın
fiyatı değiştiğinde, o maldan veya hizmetten tüketilen miktarda değişeceği için sözkonusu mal veya hizmetin tüketiminden elde edilen toplam fayda da değişecektir.
Enflasyon sebebiyle, para tutmanın maliyeti artacağından, talep edilen reel balanslar
azalacak ve paranın sağladığı toplam fayda azalacaktır. Para tutmanın fırsat maliyeti,
nominal faiz oranı olduğu için beklenen enflasyondaki artış nominal faizleri
enflasyondaki artış kadar yükseltecek ve sosyal refah kaybına sebep olacaktır. Bu kayıp
Şekil 6.8'de gösterilmiştir.
Beklenen durağan enflasyon oranının
sebep olduğu refah kaybı
Şekil 6.8
Eğer R, bu durumda para tutmanın alternatif maliyeti yükselecek ve böylelikle (m=Md/P) ,
alışverişe daha fazla zaman ve enerji harcanacak ve bu da refah kaybına yol açacaktır.
Enflasyon oranı sıfır ve dolayısıyla r = R iken, μ1=π1 oranında durağan bir enflasyon
nominal faizleri R1=r+ π1 düzeyine yükselterek, Şekil 6.9'da gösterilen taralı alan kadar
bir refah kaybına yol açacaktır. Bu alan reel para talebi fonksiyonunun m1 ve m0
aralığında belirli integrali hesaplanarak bulunabilir.
9
EM 316 Matematiksel İktisat II
K. Lopcu
ÇÜ, Ekonometri
Şekil 6.9
Örnek olarak, aşağıdaki reel para talebi fonksiyonunu ele alalım.
ln m   0   1 ln y   2 ln R
1>0, 2<0
(16)
anti logaritmasını aldığımızda,
m  e 0 . y 1 .R 2
(17)
1=1, 2= - 0,5 olduğunu varsayalım.
Değerleri yerine koyup denklem (17)'yi R için
çözdüğümüzde,
R  ( e 0
y 2
)
m
(18)
Sıfır enflasyon oranında r=R=0,04 ve y/m=5 olduğunu düşünelim. Bu durumda
denklem (18)’de e 0 
( 0 ,04 )1 / 2
 0 ,04 olacaktır.
5
Refah kaybını gelirin bir oranı
olarak hesaplamak için y=100 diyelim. Bu durumda enflasyon sıfır iken M/P=m=20
olacaktır. Şimdi yıllık yüzde 12 durağan bir enflasyon varsayalım ve enflasyondan
kaynaklanan refah kaybını hesaplayalım. Yüzde 12 yıllık enflasyon nominal faiz oranını
yüzde 16’ya yükseltecektir ( R=0,04+0,12=0,16). R=0.16 rakamı denklem (18) yerine
konduğunda şimdi y/m=10 ve M/P=m=10 olacaktır.
10
Refah kaybı rakamlar yerine
EM 316 Matematiksel İktisat II
K. Lopcu
ÇÜ, Ekonometri
konularak denklem (18)’de verilen reel balans talebinin altındaki m=10 ve m=20
aralığında kalan alan hesaplanarak bulunabilir.

20
10
2
( 0 ,04


20
100
) dm  16  m 2 dm  16 ( 20 1 )  ( 10 1 )  16 ( 0 ,05  0 ,10 )  0 ,8
10
m
Bulunan sonuç yüzde 12’lik bir enflasyonun, toplam çıktının yüzde 0,8’lik bir kısmı
kadar refah kaybına yol açacağına işaret etmektedir. Bir trilyon dolarlık bir ekonomi
için bunun anlamı 8 milyar dolarlık refah kaybıdır. Yüzde 100 enflasyon durumunda bu
kayıp toplam çıktının yüzde 3,28’ine ulaşacaktır. Başka bir deyişle, 1 trilyon dolarlık bir
ekonomi için bu kayıp 32,8 milyar dolar olacaktır. İlgili okuyucular, bu sonucu kolayca
teyit edebilir.
11