Rectangular waveguide Waveguide to coax adapter E

10.12.2015
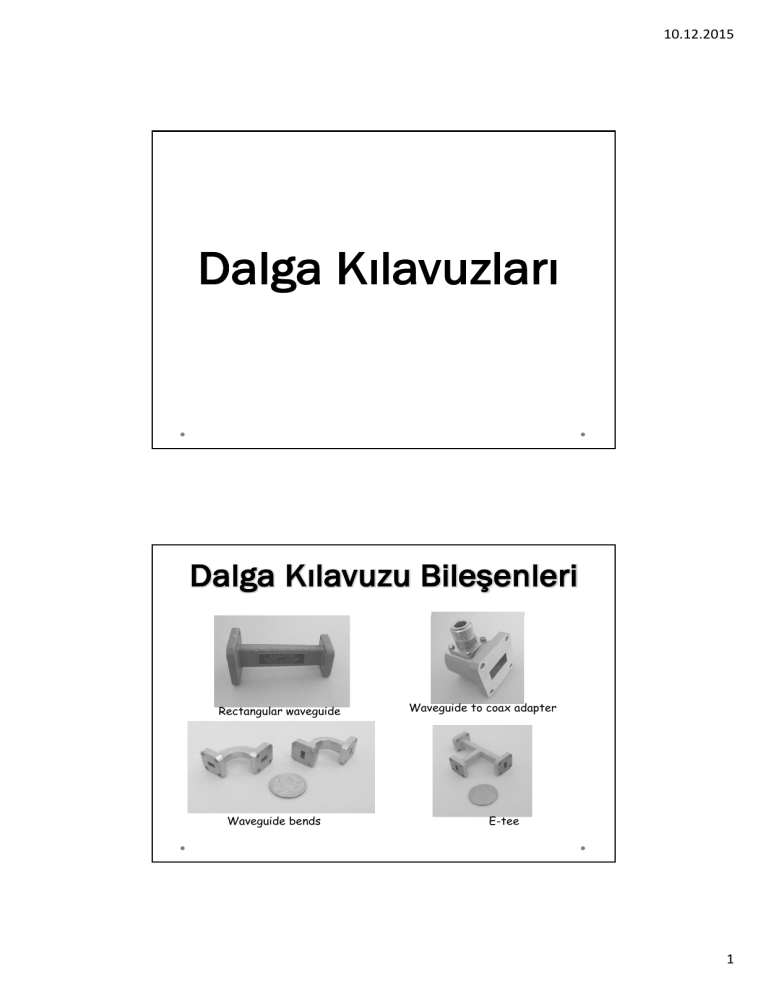
Rectangular waveguide
Waveguide bends
Waveguide to coax adapter
E-tee
1
10.12.2015
 Dalga Kılavuzları, elektromanyetik enerjiyi kılavuzlayan yapılardır.
 Dalga kılavuzları elektromanyetik enerjinin mümkün olan en az kayıpla iletilmesini
sağlayacak şekilde tasarlanırlar.
 Pratikte iki temel dalga kılavuzu tipi vardır
1-Metalik Dalga Kılavuzları: Yüksek frekanslarda, mikrodalga ve milimetre dalga
bantlarında iletim için kullanılır. Koaksiyel kablolar, içi boş dikdörtgen veya dairesel
kesitli dalga kılavuzları bu kategoride yer alırlar.
2- Dielektrik Dalga Kılavuzları: Milimetre dalgalardan daha küçük dalga boylarında ve
optik frekans bölgesinde kullanılırlar. Optik fiber kablolar bu kategoride yer alırlar.
2
10.12.2015
 Dalga kılavuzu yapılarında ‘Modal yayılım’ gerçekleşir. Elektromanyetik enerji dalga
kılavuzu içinde ‘MOD’ adı verilen belirli alan şekillerini oluşturarak yayılır.
 Paralel dalga kılavuzları iki paralel sonsuz iletken düzlemden oluşur. Elektromanyetik
enerji plakalar arasında hapsedilip iletilir. Paralel plakalar arasında elektromanyetik dalga
üç tipte bulunabilir
Transverse Electric Fields (TE- Enine elektrik alanlar)
Transverse Magnetic Flelds (TM-Enine manyetik alanlar)
Transverse Electomagnetic Fields (TEM-Enine elektromanyetik alanlar)
 Enine elektrik alanda, elektrik alan dalganın yayılım doğrultusuna diktir. Başka bir deyişle,
yayılım doğrultusunda elektrik alan bileşeni yoktur.
 Enine manyetik alanda, manyetik alan dalganın yayılım doğrultusuna diktir. Başka bir
deyişle, yayılım doğrultusunda manyetik alan bileşeni yoktur.
 Enine elektromanyetik alanda, elektrik ve manyetik alanların ikisi de yayılım doğrultusuna
diktir.
Metal duvarlar
Dalga kılavuzunun z-boyunca uzandığını düşünelim. Dalganın zboyunca değişimi
katsayısıyla orantılı olacaktır.
3
10.12.2015
Maxwell denklemini, verilen geometri için yazalım:
•
Denklemlerde z’e göre türev aşağıdaki gibi olacaktır.
Buna göre denklemleri yeniden düzenlersek
4
10.12.2015
• Benzer işlemleri
Amper denklemi için de
yaparsak, aşağıdaki eşitlikleri elde ederiz.
Maxwell denklemlerinden elde ettiğimiz 6 denklemden ‘’enine bileşenleri’’ çekelim.
Örneğin 1. denklemi aşağıdaki gibi düzenleyebiliriz:
5
10.12.2015
•
Benzer şekilde diğer denklemleri de düzenlersek:
Görüldüğü gibi elektrik ve
manyetik alanın enine bileşenleri
(x ve y), boyuna bileşenler (z)
cinsinden yazılmış !!!
Dalga kılavuzu içinde boyuna bileşenlerin durumu, yayılan modu belirler. İçi boş
dikdörtgen kesitli dalga kılavuzu içinde TEM dalgası oluşmaz!!!
 Dalga denklemleri;
 Alanların z- bileşenleri için dalga denklemlerini yazarsak;
 Dalga denklemleri, kılavuzun duvarlarındaki sınır koşulları göz önüne alınarak
çözülecektir. İki tip çözüm söz konusudur; TE(Transverse electric) ve
TM(Transverse magnetic).
6
10.12.2015
TM (Transverse Magnetic) Modunda, =0, ≠0’dır. Yani manyetik alan bileşenleri
yayılım doğrultusuna diktir, yayılım doğrultusunda manyetik alan bileşeni bulunmaz.
Bütün alan bileşenleri ’den bulunabilir. Dalga denkleminin genel çözümü;
A,B,C ve D sabit. Sınır koşulları uygulanırsa;
ve
ş
.
7
10.12.2015
 TM dalgaları için, +z yönünde ilerleyen elektrik alanın boyuna bileşeni aşağıdaki gibi
yazılır.
 B ve D sabitlerinin çarpımına U sabiti dedik. Her bir çözüm (m ve n’lerin
kombinasyonlarından oluşan) mod diye isimlendirilir.
durumda kesim frekansı;
ş
.
=0 durumu, kesim frekansını belirler. Bu
m,n=1,2,3…..
TM modunda m ve n sıfır olamaz.
8
10.12.2015
 Kesim frekansı
 Kesim dalga boyu
 Kılavuz içindeki dalga boyu
 Kılavuz içindeki faz hızı
9
10.12.2015
 TM Modu için karakteristik empedans, aşağıdaki gibi bulunur.
TM modunda
0olduğu için,
yandaki denklemlerden karakteristik
empedans;
Bulunur.
Aşağıdaki gibi
de yazılabilir.
TE (Transverse Electric) Modunda,
≠ 0, =0’dır. Yani elektrik alan bileşenleri yayılım
doğrultusuna diktir, yayılım doğrultusunda elektrik alan bileşeni bulunmaz. Bütün alan
bileşenleri ’den bulunabilir. Dalga denkleminin genel çözümü;
Maxwell denklemlerinden;
10
10.12.2015
Sınır koşulları;
 Kesim frekansı ve dalga boyu TM modu ile aynıdır!!!
 TE Modu için karakteristik empedans, aşağıdaki gibi bulunur.
TE modunda
0olduğu için, yandaki
denklemlerden karakteristik empedans;
Bulunur.
Aşağıdaki gibi
de yazılabilir.
11
10.12.2015
Örneğin, X-band dalga kılavuzunda, TM ve TE modları için kesim frekansları aşağıdaki
tabloda verilmiştir. (Dalga kılavuzu boyutları a=2.286cm, b=1.016cm)
Baskın mod:
aralığında sadece
modu yayılmaktadır.
Bu mod, Baskın Mod diye isimlendirilir.
12
10.12.2015
TEm0
Mod Kesim Frekansı
fc [GHz]
Mod Kesim Frekansı
fc [GHz]
a1 kesitli dalga
kılavuzu
a2 kesitli dalga
kılavuzu
TE10
6.94
3.48
TE20
13.88
6.97
TE30
20.82
10.44
TE40
27.76
13.92
TE50
34.72
17.44
a1 = 2.16 cm
a2 = 4.30 cm
b =1.00 cm
13
10.12.2015
Mod Kesim Frekansı
fc [GHz]
Mod Kesim Frekansı
fc [GHz]
a1 kesitli dalga kılavuzu
a3 kesitli dalga kılavuzu
TE10
6.94
4.50
TE20
13.88
9.00
TE30
20.82
13.50
TE40
27.76
18.00
TE50
34.72
22.5
TEm0
a1 kesiti, 2.16cm, a3 kesiti 3.33cm’ dir.
14
10.12.2015
Görüldüğü dalga
kılavuzunda TE20 modunun
yayıldığı görülmektedir
15
10.12.2015
16
10.12.2015
17
10.12.2015
18
10.12.2015
19
10.12.2015
20
10.12.2015
Örnek
Boyutları a=2.5 cm, b=1 cm olan dalga kılavuzu 15.1 GHz frekansının
altında çalışmaktadır. Kılavuzun içi =0, =4. 0 , r=1 olan malzeme ile
dolu olduğuna göre, Kaç tane TE ve TM modu yayılacağını bulunuz.
Kesim frekansı;
olduğuna göre kesim
frekansını aşağıdaki
gibi yazabiliriz.
a=2.5b, veya a/b=2.5, ve ;
15.1 GHz’den küçük kesim frekanslarına sahip modları hesaplamalıyız.
Yayılacak modlar;
TE01
TE02
TE10
TE20
TE30
TE40
TE50
TE11, TM11
TE21, TM21
TE31, TM31
TE41, TM41
21
10.12.2015
Örnek
Boyutları a=1.5 cm, b=0.8 cm olan dalga kılavuzunun içi =0, =4. 0 , r=1 olan malzeme ile doludur.
Verildiğine göre;
a)
Modunu
b)
Kesim frekansını
c)
Faz sabitini
d)
Yayılım sabitini
e)
Karakteristik empedansı hesaplayınız.
a) m=1 ve n=3’tür. TE13 ve ya TM13 modu yayılmaktadır.
b)
22