2. BÖLÜM

2. BÖLÜM
øùLEMSEL KUVVETLENDøRøCøLERøN LøNEER
UYGULAMALARI
øúlemsel kuvvetlendiriciler, endüstriyel elektronik uygulamaları açısından
büyük önem taúıyan bir yapı grubudur. øúlemsel kuvvetlendiriciler, endüstriyel
elektronik alanında çeúitli ölçü ve kontrol düzenlerinin gerçekleútirilmesi amacıyla
geniú ölçüde kullanılmakta, bu yapı grubu yardımıyla de÷iúik özelliklerdeki lineer
ve lineer olmayan devre fonksiyonları elde edilebilmektedir. Akım kaynakları,
negatif empedans çevirici, integral ve türev alıcılar, logaritmik ve ters logaritmik
kuvvetlendiriciler, çeúitli türden osilatör devreleri, presizyonlu do÷rultucular, ACDC çeviriciler, analog çarpma-bölme ve karekök alma devreleri, örnekleme ve
tutma devreleri, karúılaútırıcılar, Schmitt tetikleme devreleri, enstrümantasyon
kuvvetlendiricileri gibi devrelerin ve düzenlerin gerçekleútirilmesi gerekece÷i göz
önüne alınacak olursa, geniú bir çeúitlilik gösteren bu uygulamalar açısından,
iúlemsel kuvvetlendiricilerin ve bunların birer türevi olan OTA'lar (geçiú iletkenli÷i
kuvvetlendiricileri) ve Norton (akım farkı) kuvvetlendiricilerinin önemli bir rol
oynayacakları açıktır.
Bu Bölüm'de, iúlemsel kuvvetlendiricilerin lineer uygulamaları ele
alınacak, temel devre yapıları elemanın ideal olmaması durumu da göz önünde
bulundurularak incelenecek, devrelerin çalıúma bölgeleri ve bunların sınırları
belirlenecektir.
2.1. Akım Kaynakları
2.1.1. "Yüzen" yükler için akım kaynakları
Endüstriyel elektronik alanında bir çok uygulama için akım kayna÷ı
yapılarına sıkça gereksinme duyulur. Bazı uygulamalarda, gerçekleútirilecek akım
kayna÷ının büyük de÷erli akımlar vermesi de istenebilir. øúlemsel
kuvvetlendiricilerle kurulan akım kayna÷ı devreleri bu gereksinmeye bir çözüm
getirmektedir.
ENDÜSTRøYEL ELEKTRONøK
6
øúlemsel kuvvetlendiricilerle gerçekleútirilen en basit akım kayna÷ı
devreleri, faz döndüren ve faz döndürmeyen kuvvetlendirici yapılarına dayanan ve
yüzen yükler için kullanılan akım kayna÷ı yapılarıdır. Yüzen yükler için
kullanılan akım kayna÷ı devreleri ùekil-2.1'de görülmektedir.
I2
RL
+VCC
+ V2 7
VP 3
R1
6
2
+VO
VN
+Vref
I1
4
-VEE
(a)
I2
RL
+VCC
+Vref
7
VP
VN
R1
I1
3
6
2
+VO
4
-VEE
(b)
ùekil-2.1. "Yüzen yükler için akım kaynakları; a) faz döndüren yapı, b) faz döndürmeyen
yapı.
Devreyi gerçekleútirmek için kullanılan iúlemsel kuvvetlendiricinin açık
çevrim kazancı sonlu ve KV ise, kuvvetlendiricinin giriú gerilimi VIN = VP - VN sıfır
olmaz. Giriú direncinin sonsuz, ancak açık çevrim kazancının sonlu oldu÷u kabul
edilirse, devreden de yararlanılarak
I1 = I2 =
V ref - V N
R1
,
VN =-
VO
KV
LøNEER UYGULAMALAR
7
V 2 = V N -V O
ba÷ıntıları yazılabilir. Böylece, akım kayna÷ı devresinin çıkıú akımı
I2 =
V ref
V ref
V2
V2
|
R1 R1 .(1+ KV ) R1 KV . R1
(2.1)
olur. øúlemsel kuvvetlendiricinin açık çevrim kazancının yeteri kadar büyük olması
durumunda, ikinci terim ilk terimin yanında rahatlıkla ihmal edilebilir. Böylece,
devrenin çıkıú akımı
I2 =
V ref
R1
(2.2)
biçiminde yazılabilir. Akım kayna÷ının çıkıú direnci ise
RO = -
wV 2
= KV . R1
w I2
(2.3)
ba÷ıntısı yardımıyla hesaplanabilir. (2.3) ba÷ıntısından fark edilebilece÷i gibi,
akım kayna÷ı devresinin çıkıú direnci, iúlemsel kuvvetlendiricinin açık çevrim fark
iúaret kazancına ve R1 direncine ba÷lıdır. øúlemsel kuvvetlendiricinin açık çevrim
kazancı ise frekansa ba÷lıdır. Genel amaçlı iúlemsel kuvvetlendiriciler, ço÷unlukla,
frekans e÷rileri tek kutuplu düúme gösterecek biçimde kompanze edilirler. ùekil2.1'deki akım kayna÷ı devrelerinin bu tür iúlemsel kuvvetlendiricilerle kuruldukları
varsayılsın. Bu durumda iúlemsel kuvvetlendiricinin açık çevrim kazancı
KV (s) =
KVO
1+ W .s
(2.4)
úeklinde yazılabilir. Burada KVO iúlemsel kuvvetlendiricinin açık çevrim
kazancının alçak frekanslardaki de÷erini göstermektedir. W büyüklü÷ü ise
W =
1
Zc
(2.5)
úeklinde, açık çevrim transfer fonksiyonunun açısal kesim frekansı cinsinden ifade
edilebilen bir büyüklüktür. (2.3) ba÷ıntısı uyarınca
ENDÜSTRøYEL ELEKTRONøK
8
RO = R1 . KV (s)
olaca÷ından hareket edilirse, akım kayna÷ının çıkıú empedansı
Z O (s) =
KVO
. R1
1+ W .s
(2.6)
úeklinde yazılabilir. (2.6) ba÷ıntısında s yerine jZ konursa, jZ domeninde devrenin
çıkıú empedansı
Z O (jZ ) =
KVO
(2.7)
.
Z R1
1+ j
Zc
biçiminde yazılabilir. Akım kayna÷ının çıkıú empedansı, bir RO çıkıú direnci ve bir
CO çıkıú kapasitesinin paralel eúde÷eri gibi de düúünülebilir. Böylece
ZO =
1
Z
1
+j
KVO . R1 KVO . R1 .Z c
= RO / /
1
jZ C O
(2.8)
yazılabilir. (2.8) ba÷ıntısı uyarınca, devrenin çıkıú direnci
RO = KVO . R1
(2.9)
ve çıkıú kapasitesi de
CO =
1
KVO . R1 .Z c
(2.10)
ba÷ıntıları yardımıyla hesaplanabilir. Elde edilen sonuçların hem faz döndüren hem
de faz döndürmeyen yapılar için geçerli oldu÷unu belirtmekte yarar vardır.
LøNEER UYGULAMALAR
9
Örnek:
Akım kayna÷ı gerçekleútirmek üzere kullanılan iúlemsel kuvvetlendiricinin
açık çevrim kazancı KVO = 105 ve 3 dB kesim frekansı da fc = 10 Hz olsun.
Devredeki R1 direncinin de÷eri de 1 k: olarak verilsin. Bu durumda akım
kayna÷ının çıkıú direnci RO = 100 M: ve çıkıú kapasitesi de CO = 159pF olur. f=
10 kHz için akım kayna÷ının çıkıú empedansının modülünün 100 k: de÷erine
düúece÷i kolayca görülebilir.
2.1.2. Bir ucu topraklanmıú yükler için akım kayna÷ı devreleri
ùekil-2.1'de verilen devreler, iki ucu da toprak potansiyelinden yalıtılmıú
yüklerle kullanılmaya elveriúli yapılardır. Bir çok endüstriyel devre uygulamasında
ise bir ucu topraklanmıú yükler söz konusu olur. Bu tür yüklerin sürülmesi için
daha farklı devre yapılarına gereksinme duyulaca÷ı açıktır. Bu özelli÷i gösteren
çok sayıda devre yapısı bulunmaktadır. Bu bölümde, bir ucu topraklanmıú yüklerin
sürülmesi için kullanılabilecek akım kayna÷ı devrelerinden üçü ele alınarak
incelenecektir.
Çıkıú akımının bir direnç üzerindeki gerilim düúümü yardımıyla
gözlenmesi ilkesine dayanarak çalıúan bir akım kayna÷ı devresi ùekil-2.2'de
verilmiútir. Bu yapı için devreden hareketle dü÷üm denklemleri yazılacak olursa
V O -V N V N
=0
R2
R3
V ref - V P V 2 - V P
+
=0
R2
R2
V O -V 2 V P -V 2
+
- I2 =0
R1
R2
elde edilir. VN = VP oldu÷u kabul edilirse, devrenin çıkıú akımı için
§ 1
§ R 2 + R 3 R1 + 2 R 2 ·
R2 + R3 ·
¸.V ref + ¨
¸.V 2
+
I2 =¨
© 2. R2 2. R1 . R3 ¹
© 2 R 1 . R 3 2 R1 R 2 ¹
(2.11)
ENDÜSTRøYEL ELEKTRONøK
10
R2
R2
+Vref
+VCC
7
VP
3
VO
6
R1
+V2
2
VN
4
-VEE
R3
R2
I2
RL
ùekil-2.2. Tek ucu topraklanmıú yüklerin sürülmesine elveriúli akım kayna÷ı devresi.
ba÷ıntısı bulunur. (2.11) ba÷ıntısından fark edilebilece÷i gibi, R3 direncinin belirli
bir de÷eri için ikinci terim sıfır ve bunun sonucunda çıkıú akımı çıkıú geriliminden
ba÷ımsız olur. R3 direncinin bu de÷eri
2
R2
R3 =
R1 + R 2
(2.12)
ba÷ıntısıyla hesaplanabilir. Bu durumda devrenin çıkıú akımı
I2 =
V ref
R1 / / R 2
(2.13)
olur. Pratikte R1 direnci R2 direncinden yeteri kadar küçük tutulur. Bu úart altında
akım kayna÷ının çıkıú akımı
I2 =
V ref
R1
(2.14)
úeklinde belirlenebilir.
Ba÷lanacak yük direnci için sınır de÷erler
Akım kayna÷ı devresine ba÷lanacak yükün sınır de÷erleri, devreyi
gerçekleútirmek amacıyla kullanılacak iúlemsel kuvvetlendiricinin VO çıkıú
geriliminin sınırları ile belirlidir. øúlemsel kuvvetlendiricinin çıkıú gerilimi VCC ve
LøNEER UYGULAMALAR
11
-VEE besleme gerilimlerine ulaúamaz; ancak bu gerilimlere birer doyma gerilimi
kadar yaklaúabilir.
Pozitif yöndeki doyma gerilimini Vsat, negatif yöndeki doyma gerilimini de
Vsat ile gösterelim. Böylece, iúlemsel kuvvetlendiricinin çıkıú geriliminin
alabilece÷i maksimum ve minimum de÷erler
'
V omaks = VCC - V sat
V omin = VEE V sat '
(2.15)
(2.16)
ba÷ıntıları yardımıyla hesaplanabilir. Öte yandan devrenin çıkıú gerilimi yazılırsa
V 2 = V O - I 2 . R1
bulunur. Vref = V > 0 için I2 = Vref/R1 = V/R1 olur. Böylece
V 2maks = V Omaks - I 2 . R1 = V Omaks - V ref
V 2maks = V CC - V sat -V
(2.17)
sınır de÷eri elde edilir. Buna göre, yükün uçlarındaki gerilimin de÷eri V2maks
de÷erinden küçük ya da en fazla bu sınır de÷ere eúit olmalıdır. Elde edilen bu sınır
de÷er yardımıyla pozitif yön için yükün maksimum de÷eri hesaplanırsa
R Lmaks1 . I L = V 2maks = V Omaks -V
RL d
V Omaks - V ref
IL
(2.18)
úartı bulunur. Bu úart uyarınca, çıkıúa olabildi÷ince büyük bir yük ba÷layabilmak
için Vref << VOmaks seçilmelidir. Uygulamada, Vref = V referans kayna÷ı düúük
de÷erli ve bir-iki volt mertebesinde seçilir; ayrıca R2 >> R1 yapılır. Böylece
iúlemsel kuvvetlendiricinin ve Vref gerilim kaya÷ının yüklenmesi önlenmiú olur.
Vref = -V < 0 için I2 = -V/R1 olur. Bu durumda
V 2 min = V Omin +V = - V EE + V sat +V
(2.19)
ENDÜSTRøYEL ELEKTRONøK
12
sınır de÷eri elde edildi÷inden, çıkıúa ba÷lanabilecek maksimum yük
RL d
V 2 min V Omin +V
=
I2
I2
(2.20)
ba÷ıntısı yardımıyla hesaplanabilir.
Bir ucu topraklanmıú yükler için akım kayna÷ı devreleri çesitli biçimlerde
kurulabilir. Bu yapılardan bir di÷eri ùekil-2.3'de gösterilmiútir.
ùekil-2.3. Bir ucu topraklanmıú yükler için di÷er bir akım kayna÷ı devresi.
Bu devreden hareket edilirse
V 4 = -V 3 = V ref +
R2
.V 2
R3
V 4 -V 2 V 2
- - I2 =0
R1
R3
ba÷ıntıları yazılabilir. Ba÷ıntılarda V4 büyüklü÷ünün elimine edilmesiyle, I2 çıkıú
akımı Vref ve V2 gerilimleri cinsinden ifade edilebilir. Bu yapılırsa
V ref R2 - R3 - R1
+
.V2
I2 =
R1
R1 . R3
eúitli÷i elde edilir. R3 = R2 - R1 alınırsa, ba÷ıntıdaki ikinci terim sıfır ve çıkıú akımı
da çıkıú geriliminden ba÷ımsız olur. Böylece, çıkıú akımı
LøNEER UYGULAMALAR
I2 =
13
V ref
R1
(2.21)
úeklinde Vref akımı ve R1 direnci cinsinden belirlenebilir.
"Howland" akım kayna÷ı
Bir ucu topraklanmıú yükler için kullanılabilecek bir di÷er akım kayna÷ı
yapısı da Howland akım kayna÷ı olarak isimlendirilen ve ùekil-2.4'de gösterilen
akım kayna÷ı yapısıdır.
R2 = D.R1
+VCC
+VI1
R1
R3
+VI2
4
VN
2
VP
3
6
+VO
7
IL
R4 = ß.R3
RL
-VEE
ùekil-2.4. Howland akım kayna÷ı devresi.
Bu devrede
V i1 . R2 +V O . R1 D .V i1 +V O
=
1+ D
R1 + R2
V i2 -V P V O -V P
+
I L = I 3+ I 4 =
E .R3
R3
VN =
yazılabilir. Öte yandan
V O = KV (s).(V P - V N )
V P = I L .RL
úeklindedir. Bütün bunlar biraraya getirilecek olursa
ENDÜSTRøYEL ELEKTRONøK
14
IL =
E .(1+ D + KV (s)).V i 2 - D . KV (s).V i 1
E (1+ D + KV (s)). R3 + R L .(1+ D )(1+ E ) + R L KV (s)( E - D )
(2.22)
bulunur.
D = E , KV ( s) >> (1+D),
KV ( s) .R3 >> RL.(1+D).(1+E)
olması halinde, yük akımı
IL =
V i 2 -V i1
R3
(2.23)
ba÷ıntısı yardımıyla hesaplanabilir. Devrenin çıkıú direnci hesaplanırsa
RO = R3
(1+ D + KV (s)). E
(1+ E )(1+ D ) + KV (s).( E - D )
(2.24)
ba÷ıntısı elde edilir. KVO >> 1 oldu÷u kabul edilecek olursa (2.24) ba÷ıntısı
RO = R3 .
E
E -D
biçimini alır. D = E ise devrenin çıkıú direnci sonsuza (pratikte çok büyük
de÷erlere) gider. Devrenin çıkıú direnci eleman toleranslarına ba÷lıdır. En kötü
durumda
R1 = R1 .(1+ k), R2 = D . R1 .(1- k), R3 = R1 .(1- k), R4 = D . R1 .(1+ k)
olaca÷ı dikkate alınırsa, devrenin çıkıú direnci
RO =
R3
4.k
(2.25)
R1 den R4 'e kadar olan dirençlerin de÷erleri kontrol edilerek çıkıú direnci çok
büyük de÷erlere getirilebilir. Kararlılı÷ın sa÷lanması için R2 direncine paralel
düúük kapasiteli bir kondansatör ba÷lanır.
Vi1 = 0 , Vi2 = Vref ve D = E için iúlemsel kuvvetlendiricinin VO çıkıú
gerilimi
LøNEER UYGULAMALAR
15
V O = RL
(1+ D ). KV (s) V ref
1+ D + KV (s) R3
(2.26)
ba÷ıntısıyla verilmektedir. øúlemsel kuvvetlendiricinin açık çevrim kazancının çok
büyük olması durumunda VO çıkıú gerilimi ba÷ıntısı
V O = R L .(1+ D ).
V ref
R3
(2.27)
úeklini alır. Ba÷ıntıdan fark edilebilece÷i gibi, iúlemsel kuvvetlendiricinin çıkıú
gerilimi yük direnci ile orantılıdır. Bu nedenle, devre, sabit ölçü akımlı ve lineer
ölçekli direnç ( yahut empedans) ölçer düzeni gerçekleútirilmesine uygundur.
Yük direnci üzerinde düúecek maksimum gerilim, iúlemsel
kuvvetlendiricinin çıkıú geriliminin maksimum de÷eri olan VOmaks ile sınırlıdır.
(2.27) ba÷ıntısından hareket edilecek olursa
V Omaks = R Lmaks .(1+ D )
V ref
R3
bulunur. Buna göre, yük direncinin maksimum de÷eri
R Lmaks =
V Omaks
R3
(1+ D ).V ref
(2.28)
olacaktır. Baúka bir deyiúle, akım kayna÷ına ba÷lanacak yük direnci
RL d
V Omaks
R3
(1+ D ).V ref
(2.29)
úartını sa÷lamalıdır.
Buraya kadar ele alınan devrelerde akım kayna÷ının verebilece÷i
maksimum akım, devreyi gerçekleútirmek üzere kullanılan iúlemsel
kuvvetlendiricinin maksimum çıkıú gerilimi ve akımı ile sınırlı kalmaktadır. Bir
çok uygulamada ise bundan daha büyük de÷erli akımlara gereksinme duyulur. Bu
tür devreler bir sonraki bölümde ele alınacaktır.
ENDÜSTRøYEL ELEKTRONøK
16
2.1.3. Büyük akımlı akım kayna÷ı devreleri
Büyük akımlara gereksinme duyuldu÷unda, sadece iúlemsel kuvvetlendiricilerle
gerçekleútirilen akım kayna÷ı yapıları, çıkıú akımı iúlemsel kuvvetlendiricinin
verebilece÷i maksimum akım ile sınırlı kalaca÷ından, yetersiz olurlar. Bu nedenle,
büyük akım de÷erlerinin gerekli oldu÷u uygulamalarda iúlemsel kuvvetlendiricitranzistor (BJT, JFET, MOSFET) kombinezonları kullanılır. BJT-iúlemsel
kuvvetlendirici kombinezonu için bir devre yapısı örne÷i ùekil-2.5'de verilmiútir.
+VCC+
+
+VCC
RL
V2
I2
-
7
3
+Vref
6
2
T
4
-VEE
R1
ùekil-2.5. BJT-iúlemsel kuvvetlendirici kombinezonu ile akım kayna÷ı devresi.
Bu yapıda, uçlardan birinin sabit potansiyelde tutulabilece÷i açıktır. Bir
ucu topraklanmıú ve büyük akımlı akım kaynakları, sadece tranzistorlar
kullanılarak da gerçekleútirilebilir. Ancak, sadece BJT, JFET yahut MOSFET
kullanılarak gerçekleútirilen yapılarda çıkıú akımı VBE'ye yahut VGS'ye ba÷ımlılık
gösterir. øúlemsel kuvvetlendiricilerin de kullanılmasıyla bu etki ortadan
kaldırılmaktadır. ùekil-2.5'deki yapıda, I2 çıkıú akımı ve RO çıkıú direnci Vref > 0
olması úartı altında
1 ·
V ref §
.¨1I2 =
¸
R1 © E F ¹
(2.30)
RO = E F . r ce
(2.31)
ba÷ıntıları yardımıyla hesaplanabilir.
Benzer bir yapı JFET ve iúlemsel kuvvetlendirici yardımıyla da
gerçeklestirilebilir. Böyle bir yapı ùekil-2.6'da verilmiútir.
LøNEER UYGULAMALAR
17
+
+VCC
+
+VCC
RL
V2
+Vref
I2
-
7
3
6
T
2
4
R1
-VEE
ùekil-2.6. JFET ve iúlemsel kuvvetlendirici kullanılarak büyük akımlı akım kayna÷ı
gerçekleútirilmesi.
ùekil-2.6'daki akım kayna÷ı devresinin çıkıú akımı
I2 =
V ref
R1
(2.32)
úeklindedir. Devrenin çıkıú direnci ise, iúlemsel kuvvetlendiricinin sonlu KV açık
çevrim kazancı ile sınırlıdır. Devreden hareket edilirse
dV DS = - dV 2
dV GS = dV G - dV S = - KV . R1 .dI 2 - R1 .dI 2 = - KV . R1 .dI 2
yazılabilir. Öte yandan JFET'in eúde÷er devresinden
dI 2 = g m . dV GS +
1
r ds
. dV DS
ba÷ıntısı elde edilir. Bunların biraraya getirilmesiyle akım kayna÷ının çıkıú direnci
için
ENDÜSTRøYEL ELEKTRONøK
18
RO = -
dV2
dI 2
= r ds .(1+ KV . g m . R1 ) | P . KV . R1
(2.33)
eúitli÷i bulunur. Bu ba÷ıntıdaki P büyüklü÷ü JFET'in kuvvetlendirme katsayısıdır
ve de÷eri P = gm.rDS =150 civarındadır. Elde edilen sonuç daha önce elde edilen
(2.3) ba÷ıntısı ile karúılaútırılırsa, bu devrenin çıkıú direncinin, JFET kullanılmadan
sadece iúlemsel kuvvetlendirici ile gerçekleútirilen akım kayna÷ı yapısına göre P
defa daha büyük olaca÷ı kolayca görülebilir.
KV açık çevrim kazancının frekansa ba÷lı oldu÷u göz önüne alınırsa,
devrenin çıkıú empedansı
Z O = KV . P . R1 =
KVO
Z
1+ j
ZC
P . R1
(2.34)
biçiminde yazılabilir. Daha önce iúlemsel kuvvetlendiricilerle kurulan akım
kayna÷ı devrelerinde yapıldı÷ı gibi, devrenin çıkıú empedansı RO = P.KVO.R1
de÷erinde bir direnç ile CO=1/P.KVO.R1.ZC de÷erli bir kapasitenin paralel eúde÷eri
gibi düúünülebilir.
+
+VCC
+
+VCC
+Vref
RL
V2
-
7
I2
3
6
2
T1
T2
4
-VEE
R2
R1
ùekil-2.7. JFET ve güç tranzistorunun Darlington çifti oluúturacak úekilde ba÷lanması.
Yüksek de÷erli çıkıú akımları gerekti÷inde, devreyi kurmak üzere bir güç
JFET'inden yararlanılabilir, yahut küçük akımlı bir JFET ile bir güç tranzistoru
Darlington çifti oluúturacak úekilde ba÷lanır. Böyle bir akım kayna÷ı devresi ùekil2.7'de görülmektedir. Geçitten içeriye do÷ru akım akmadı÷ından yapının
özellikleri de÷iúmez. Baúka bir deyiúle, Vref > 0 için devrenin çıkıú akımı
LøNEER UYGULAMALAR
19
I2 =
V ref
R1
(2.35)
ve çıkıú direnci de
R O = P 1 . K V . R1
(2.36)
olur.
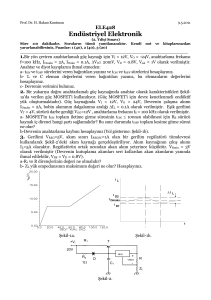
JFET ve faz döndüren kuvvetlendirici olarak çalıúan bir iúlemsel
kuvvetlendiricinin biraraya getirilmesiyle de akım kayna÷ı devresi gerçekleútirmek
mümkündür. Böyle bir yapı ùekil-2.8'de verilmiútir. Bu yapıda, Vref = -V < 0 için
+VCC+
+
+VCC
RL
V2
-
I2
7
-Vref
3
6
2
T
4
-VEE
ùekil-2.8. JFET ve faz döndüren kuvvetlendirici olarak çalıúan iúlemsel kuvvetlendirici ile
akım kayna÷ı.
devrenin I2 çıkıú akımı
I2 = -
V
R1
(2.37)
ve çıkıú direnci de
R O = P . KV . R1
(2.38)
úeklindedir. JFET"in kesime gitmemesini sa÷layabilmek üzere, Vref gerilimi daima
negatif olmak zorundadır. Bu yapıda I2 çıkıú akımı Vref kayna÷ı üzerinden
akaca÷ından, yapı büyük akımlar akıtmaya elveriúli de÷ildir.
ENDÜSTRøYEL ELEKTRONøK
20
R1
+VCC
7
+Vref
3
6
T
2
4
+
-VEE
RL
V2
I2
-VEE
ùekil-2.9. p kanallı JFET ve iúlemsel kuvvetlendirici ile kurulan ve uçtan dıúarıya do÷ru
akım akıtmak üzere düzenlenmiú akım kayna÷ı devresi.
Buraya kadar ele alınan akım kayna÷ı devreleri uçtan içeriye do÷ru akım
akıtmak üzere düúünülmüú yapılardır. Ancak, bazı uygulamalarda, uçtan dıúarıya
do÷ru akım akıtacak akım kaynaklarına da gereksinme duyulabilir. Böyle
durumlarda p kanallı bir JFET kullanılması zorunlulu÷u ortaya çıkar. p kanallı
JFET ve iúlemsel kuvvetlendirici ile kurulan ve uçtan dıúarıya do÷ru akım vermek
üzere tasarlanmıú bir akım kayna÷ı devresi ùekil-2.9'da görülmektedir. Bu yapıda
Vref < 0 için devrenin çıkıú akımı
I2 = -
V ref
R1
(2.39)
ve çıkıú direnci de
R O = P . KV . R1
(2.40)
olur. p kanallı JFET yerine n kanallı JFET kullanarak da çözüme gitmek
mümkündür. n kanallı JFET ve iúlemsel kuvvetlendirici ile kurulan ve uçtan dıúa
do÷ru akım akıtan böyle bir akım kayna÷ı devresi ùekil-2.10'da verilmiútir. Bu
yapıda Vref= -V < 0 oldu÷u göz önüne alınırsa , devrenin çıkıú akımı ve çıkıú
direnci, iúlemsel kuvvetlendiricinin açık çevrim kazancı ve dıú devre elemanları
cinsinden
I2 = -
V
R1
(2.41)
LøNEER UYGULAMALAR
21
(2.42)
R O = KV . R1
úeklinde ifade edilebilir. JFET'in S kaynak ucu çıkıú ucu görevini üstlenir. Çıkıúın
kaynak ucundan alınması, çıkıú akımını etkilemez. Devrenin kararlı kalabilmesi
için gerekli olan negatif geribesleme úu úekilde sa÷lanmaktadır:
+VCC
R1
7
3
6
T
2
+Vref
4
D
-VEE
+
V2
RL
I2
-VEE
ùekil-2.10. n kanallı JFET ve iúlemsel kuvvetlendirici ile kurulan akım kayna÷ı yapısı
Çıkıú akımının de÷erinin düúmesi halinde VP gerilimi yükselir. Bununla
Kuvvetlendiricinin çıkıú gerilimi, dolayısıyla JFET'in geçit gerilimi bir miktar
pozitife do÷ru kayar ve bu da akımı arttıracak yönde etki eder. Devrenin çıkıú
direnci ise, (2.42) ba÷ıntısından da izlenebilece÷i gibi, önceki devrenin çıkıú
direncine göre 1/P oranında daha düúük olmaktadır.
Büyük giriú gerilimlerinde JFET'in geçit - kanal jonksiyonu geçirme
yönünde
kutuplanabilir.
Bu
durumun
ortaya
çıkmasıyla, iúlemsel
kuvvetlendiricinin çıkıú gerilimi iletimde olan jonksiyon uzerinden
kuvvetlendiricinin faz döndürmeyen (P) giriúine gelir ve pozitif geribesleme
oluúur. Bu úekilde ortaya çıkabilecek bir pozitif geribeslemeyi önlemek üzere,
devrede bir D diyodu kullanılmıútır. D diyodunun kullanılması halinde, bu diyot,
iúlemsel kuvvetlendiricinin çıkıú gerilimini Vref geriliminin bir VBEon iletim yönü
gerilimi kadar üzerindeki bir de÷ere kenetler.
JFET ve iúlemsel kuvvetlendirici yardımıyla da gerçekleútirilen ve daha
önce ùekil-2.6'da verilmiú olan yapının benzeri MOSFET kullanılarak da
kurulabilir. MOSFET ve iúlemsel kuvvetlendirici kullanılarak gerçekleútirilen
ENDÜSTRøYEL ELEKTRONøK
22
akım kayna÷ı devreleri ùekil-2.11’de görülmektedir. ùekil-2.11a’da N kanallı
MOSFET, ùekil-2.11b’de de P kanallı MOSFET kullanılmıútır. Bu devrelerin tüm
özellikleri ùekil-2.6’daki devre ile aynıdır.
+VCC+
+
+VCC
RL
V2
-
I2
7
+Vref
3
6
T
2
4
R1
-VEE
(a)
-VEE+
-
+VCC
RL
V2
+
+Vref
I2
7
3
6
2
T
4
R1
-VEE
(b)
ùekil-2.11. MOSFET ve iúlemsel kuvvetlendirici kullanılarak büyük akımlı akım kayna÷ı
gerçekleútirilmesi. a) N kanallı MOSFET ile kurulan devre , b) P kanallı MOSFET ile
kurulan devre, Vref < 0.
ùekil-2.11a 'daki akım kayna÷ı devresinin çıkıú akımı
I2 =
V ref
R1
úeklindedir. Her iki devrenin çıkıú empedansı
(2.43)
LøNEER UYGULAMALAR
Z O = KV . P . R1 =
23
KVO
1+ j
Z
ZC
P . R1
(2.44)
olur. Daha önce JFET ve iúlemsel kuvvetlendiricilerle kurulan akım
kayna÷ıdevrelerinde karúılaúıldı÷ı gibi, devrenin çıkıú empedansı RO = P.KVO.R1
de÷erinde bir direnç ile CO=1/P.KVO.R1.ZC de÷erli bir kapasitenin paralel eúde÷eri
gibi düúünülebilir.
øki yönde akım akıtabilen, büyük akımlı akım kaynakları
Buraya kadar ele alınan büyük akımlı akım kayna÷ı devrelerinin önemli bir
sakıncası, bu yapıların sadece tek yönde akım akıtabilmeleridir. p ve n kanallı
JFET'lerle kurulan akım kayna÷ı yapılarının biraraya getirilmeleri halinde, bu
problem kolayca çözülebilir. Bu úekilde gerçekleútirilmiú bir akım kayna÷ı devresi
ùekil-2.12'de görülmektedir.
Sükunette V1 = 0 oldu÷undan VP1 ve VP2 gerilimleri
3
3
V P 1 = .V CC , V P 2 = - .V EE
4
4
de÷erlerini alırlar. Bu durumda devrenin çıkıú akımı
I D1 =
V P - (-V EE )
V CC - V P 1
, I D2 = 2
R1
R1
olmak üzere
I 2 = I D1 - I D2 =
V CC V EE
4. R1 4. R1
úeklinde yazılabilir. VCC = -VEE alınması durumunda I2 = 0 olur.
ENDÜSTRøYEL ELEKTRONøK
24
+VCC
+
+V CC
+V CC
R
4
2
3
6
T1
+
VP1
+V1
R1
7
3R
I D1
+
-V EE
+
+V CC
3R
V P2
+V 2
I D2
7
3
2
R
+
6
I2
T2
4
-V +
EE
-V EE
R1
-V EE
ùekil-2.12.Her iki yönde de akım akıtabilen JFET’li büyük akımlı akım kayna÷ı devresi.
V1 giriú geriliminin V1 > 0 olması durumunda
3
1
V P 1 = V CC + V 1
4
4
olur. Baúka bir deyiúle, VP1 gerilimi V1/4 kadar yükselir. Böylece, ID1 akımı
I D1
3
1
V CC - V CC - V 1
4
4
=
R1
I D1 =
1
(V CC - V 1 )
4. R1
olur. Buna göre, ID1 akımı V1/4R1 kadar azalmaktadır. Buna karúılık, ID2 akımı aynı
oranda artar. Buradan hareketle çıkıú akımı hesaplanırsa
I2 = -
V1
2. R1
(2.45)
LøNEER UYGULAMALAR
25
olur. Ba÷ıntıdan fark edilebilece÷i gibi, pozitif giriú gerilimleri için çıkıú akımı
negatif de÷erlidir.
V1 < 0 olması halinde ise ID2 azalır, ID1 artar; çıkıú akımı pozitif olur.
Çıkıú akımının dalgalanma aralı÷ı, devrede kullanılan JFET'lerden birinin
yahut di÷erinin kesime girdi÷ı gerilim de÷eri ile sınırlıdır. Bu úart, V1 giriú
geriliminin V1 = VCC yahut V1 = -VEE de÷erlerini alması halinde yerine gelir.
JFET'lerden birinin kesime gidebilmesi için, bunun geçit geriliminin VCC den
büyük ya da -VEE den küçük olması gerekir. Bunun için de iúlemsel
kuvvetlendiricinin besleme gerilimlerinin daha büyük tutulması zorunlu olur.
Baúka bir deyiúle
V +CC > V CC , V +EE > V EE
olmalıdır.
n ve p kanallı JFET'ler ve iúlemsel kuvvetlendiricilerle kurulan bu
devrenin sıfır noktası kararlılı÷ı iyi de÷ildir. Kararlılı÷ın iyi olmaması, çıkıú
akımının büyük de÷erli iki akımın farkı olmasının bir sonucudur. Bunun yanısıra,
farkı alınan bu iki akımın besleme geriliminden de etkilenece÷i yukarıdaki
ba÷ıntılardan kolayca fark edilebilir. Bu sakıncaları gidermek üzere kurulan bir
di÷er devre ùekil-2.13'de görülmektedir.
Bu yapı, üç iúlemsel kuvvetlendirici , bir n kanallı MOSFET ve bir de p
kanallı MOSFET içermektedir. Güç MOSFET'lerinin kullanılmasıyla, bu yapı
yardımıyla büyük akımlar verebilen akım kayna÷ı devreleri gerçekleútirilmesi de
mümkündür. Çıkıú tranzistorlarının sürülmesi, bir önceki JFET'li devredekinden
daha farklıdır. ùekil-2.13'den fark edilebilece÷i gibi, çıkıú tranzistorları giriúteki
iúlemsel kuvvetlendiricinin pozitif ve negatif besleme gerilimi kaynaklarından
çekti÷i I3 ve I4 akImlarıyla orantılı V3 ve V4 gerilimleriyle sürülmektedir. Buna
göre
V 3 = I 3 . R2 ,
I D1 =
V 4 = I 4 . R2
V 3 R2
V
R
= I 3 , I D2 = 4 = 2 I 4
R1 R1
R1 R1
ENDÜSTRøYEL ELEKTRONøK
26
+VCC
+V
+
+V
CC
CC
+
R
+
R2
V3
I3
3
+
I5
T
7
1
+
2
V1
6
3
7
V3
4
2
-
1
6
R3
4
+V 2
I2
7
I4
3
+
V4
+
6
2
R2
T2
+
4
-V EE
-V +
EE
R1
V4
-V EE
ùekil-2.13. Düúük sükunet akımlı akım kayna÷ı devresi.
I 2 = I D1 - I D 2 =
R2
( I3 - I4 )
R1
úeklindedir. Devredeki ilk kat gerilim izleyici olarak kurulmuútur. Bu gerilim
izleyici devresinin çıkıú akımı
I5 =
V1
R3
úeklindedir. Kural gere÷i, iúlemsel kuvvetlendiricinin akımlarının toplamı sıfırdır.
Dolayısıyla
I5 = I3 - I4
olur. Bütün bunlar biraraya getirilecek olursa
I2 =
R2
V1
R1 . R 3
(2.46)
LøNEER UYGULAMALAR
27
bulunur. R2 = R3 yapılırsa
I2
V1
R1
(2.47)
elde edilir. Sükunette V1 = 0 olaca÷ından, besleme kaynaklarından çekilen I3 ve I4
akımları I3 = I4 = IR úeklinde iúlemsel kuvvetlendiricinin sükunet akımına eúittirler.
Bu nedenle I5 = 0 olur. Dolayısıyla çıkıú akımı da sıfır olur.
V1 > 0 ise I3 > I4 olaca÷ından, I2 çıkıú akımı üst yarıdevre üzerinden akar
ve alt yarıdevre kesime gider.
V1 < 0 olması halinde ise bunun tersi olur. Çıkıú akımı alt yarıdevre
üzerinden akar ve üst yarıdevre kesime gider
V1 = 0 durumunda çıkıú tranzistorlarından
I D1 R
I D2 R
R2
I
R1 R
sükunet akımları akar.
Bütün bunlardan fark edilebilece÷i gibi, akım kayna÷ı devresi AB
sınıfında çalıúmaktadır. Devrenin sükunet akımı küçük de÷erli iki büyüklü÷ün
farkı biçimindedir. Bu nedenle, devrenin sıfır noktası kararlılı÷ı da bir önceki
JFET'li devreninkine göre çok daha iyidir. Ayrıca, devrenin veriminin yüksek
oldu÷unu belirtmekte de yarar vardır. Daha önce de belirtildi÷i gibi, çıkıú
tranzistoru olarak güç MOSFET'lerinin kullanılmasıyla büyük de÷erli çıkıú
akımları elde etmek de mümkündür. Büyük akımlarla çalıúma halinde, kullanılacak
güç tranzistorlarının akım, gerilim ve güç sınır de÷erlerine dikkat edilmesi ve
gerekli so÷utucunun tasarlanıp devreye monte edilmesi gerekece÷i açıktır.
2.2. Negatif empedans çevirici yapısı ve uygulamaları
Bazı devre uygulamalarında negatif dirence yahut negatif iç dirençli
gerilim kayna÷ına gereksinme duyulabilir. Negatif direnç ve negatif iç dirençli
gerilim kayna÷ı yapıları iúlemsel kuvvetlendirici yardımıyla kolayca
gerçekleútirilebilen yapılardır.
Direnç tanımı gere÷i R = V/I úeklindedir ve bir iki uçluda akım ve gerilim
yönlerinden biri referans yönüne göre zıt yönde ise V/I < 0 olur. Bu durumda
negatif direnç söz konusudur.
ENDÜSTRøYEL ELEKTRONøK
28
Negatif direnç, sadece, aktif elemanlar kullanılarak gerçekleútirilebilir.
Aktif elemanlar kullanılarak gerçekleútirilen bu devreler negatif empedans
çeviriciler olarak isimlendirilirler ve NIC ( Negative Impedance Converter)
sembolü ile gösterilirler. Negatif empedans çevirici yapısını iki farklı úekilde
gerçekleútirmek mümkündür:
-VNIC : Yönü sabit tutulan akım için gerilimin yönünü de÷iútiren çeviriciler;
-INIC : Yönü sabit tutulan gerilim için akımın yönünü de÷iútiren çeviriciler.
Gerçekleútirilmesi daha kolay oldu÷undan, burada INIC yapıları ele alınacaktır.
Yönü sabit tutulan gerilim için akımın yönünü de÷iútiren çeviricinin
(INIC) eúde÷er devresi ùekil-2.14'de verilmiútir.
ødeal durumda, negatif empedans çeviricinin tanım ba÷ıntıları
V 1 = V 2 +0. I 2
(2.48)
I 1 = 0.V 2 - I 2
úeklindedir. Bu úartları yerine getirecek bir devre, gerilimle yönetilen bir gerilim
kayna÷ı ve akımla yönetilen bir akım kayna÷ı yardımıyla gerçekleútirilebilir.
Devrenin kurulabilmesi için gerekli olan iki fonksiyon tek bir iúlemsel
kuvvetlendirici yardımı ile gerçekleútirilebilir. Böyle bir yapı ùekil-2.15'de
görülmektedir.
+
+
I1
V1
-
I2
V2 = V1
I1 = - I2
ùekil-2.14. INIC eúde÷eri.
-
LøNEER UYGULAMALAR
29
R
I1
+V1
+
-
+V2
+VO
R
I2
ùekil-2.15. Tek bir iúlemsel kuvvetlendirici yardımıyla kurulan INIC devresi.
øúlemsel kuvvetlendirici ideal kabul edilirse, VN = VP dolayısıyla V1 = V2
olaca÷ından
V O = V 2 + I 2 .R
yazılabilir. Bu durumda 1 giriúinden akan I1 akımı ile 2 giriúinden akan I2 akımı
arasındaki iliúki
I1 =
V 2 -V O
= - I2
R
(2.49)
úeklindedir. ùekil-2.14'den fark edilebilece÷i gibi, devreye negatif ve pozitif
geribeslemeler birlikte uygulanmaktadır. Bu nedenle, devrenin kararlılı÷ının
incelenmesinde de yarar vardır. Devrenin iki kapısına ba÷lanan devrelerin bu
dü÷ümlere gösterecekleri toplam eúde÷er dirençleri sırası ile R1 ve R2 ile
gösterelim. Bu durumda elde edilecek devre ùekil-2.16'da verilmiútir. Pozitif
geribesleme gerilimi
V P =V O
R1
R1 + R
ve negatif geribesleme gerilimi de
V N =V O
R2
R2 + R
ENDÜSTRøYEL ELEKTRONøK
30
VO
R
R
+ -
R1
R2
ùekil-2.16. 1 ve 2 dü÷ümlerine gelen eúde÷er dirençler.
úeklindedir. VN > VP ise devrenin kararlı olaca÷ı açıktır. Bu úartın yerine
gelebilmesi için de
R1 R2
olması gerekir.
Negatif empedans çevirici devresi, negatif direnç elde etmek üzere
kullanılabilir. Negatif direnç elde etmek üzere kurulan devre ùekil-2.17'de
verilmiútir.
R
R
+-
+V1
I1
+
V2
I2
R2
ùekil-2.17. INIC ile negatif direnç elde edilmesi.
Devrenin 1 kapısına pozitif bir V1 gerilimi uygulanırsa
-
LøNEER UYGULAMALAR
31
I1 = - I2 = -
V1
R2
V1
= - R2
I1
(2.50)
elde edilir. (2.50) ba÷ıntısından fark edilebilece÷i gibi, pozitif bir gerilim
uygulanmasına ra÷men, 1 kapısından negatif bir akım akmaktadır. 1 kapısına
ba÷lanan devrenin R1 iç direnci 2 kapısına ba÷lanan R2 direncinden küçük oldu÷u
sürece devre kararlıdır. Aynı özelli÷i R2 direncini 1 kapısına ba÷layarak da elde
etmek mümkündür.
De÷iúken iúaretler için R2 direnci yerine bir Z2 empedansı konabilece÷i ve
böylece negatif bir empedans elde edilebilece÷i açıktır.
INIC kullanılarak negatif çıkıú dirençli gerilim kayna÷ı gerçekleútirmek de
mümkündür. øç dirençli bir kaynakta kayna÷ın çıkıú gerilimi
V = V O - I. RO
R
R
+R1
+
V1
I1
I2
VO
-
+
V2
-
ùekil-2.18. Negatif iç dirençli kaynak gerçekleútirilmesi.
úeklinde VO açık devre gerilimi ve RO çıkıú direnci cinsinden yazılabilir. Normal
bir iç dirençli kaynakta RO > 0 dır; dolayısıyla I çıkıú akımı arttıkça V çıkıú
ENDÜSTRøYEL ELEKTRONøK
32
gerilimi azalır. Negatif çıkıú dirençli bir kaynakta ise I arttıkça V de artmaktadır.
Negatif iç dirençli bir kayna÷ın ne úekilde gerçekleútirilece÷i ùekil-2.18'de
gösterilmiútir.
Devrede çıkıú gerilimi
V 2 = V 1 = V O - I. R1
I1 = - I2
(2.51)
V 2 = V O + I 2 . R1
úeklindedir. Bu nedenle, çıkıú direnci de
RO = -
dV 2
= - R1
dI 2
(2.52)
olur. Negatif iç dirençli bir kaynak, elektronik bir sistemde uzun bir hattın
gösterece÷i direncin kompanze edilmesi amacıyla kullanılabilir.
Jiratör
Jiratör, herhangi bir empedansı bu empedansın dualine çevirebilen bir
transformasyon devresidir. Jiratörün devre sembolü ùekil-2.19'da gösterilmiútir.
Rg
I1
I2
+V1
+V2
ùekil-2.19. Jiratör devre sembolü.
Jiratörün tanım ba÷ıntıları:
LøNEER UYGULAMALAR
33
I 1 = 0.V 1 +
I2 =
1
Rg
1
Rg
.V 2
.V 1+0.V 2
úeklindedir. Bu ba÷ıntılar matrisel olarak
0 · § V 1·
§1 / Rg
§ I 2·
¸ .¨ ¸
¨ ¸ = ¨
1 / R g ¹ © V 2¹
© I 1¹
© 0
I1
I2
+V1
I1 = V2/Rg
(2.53)
+V2
I2 = V1/Rg
ùekil-2.20. Gerilimle yönetilen iki akım kayna÷ı ile jiratör devresi.
biçiminde yazılabilir. Jiratör devresinde, bir taraftaki akım di÷er taraftaki gerilim
ile orantılıdır. Jiratör, aktif elemanlar kullanılarak gerçekleútirilebilen bir devre
elemanıdır. Ba÷ıntılardan hareket edilirse, jiratörün gerilimle yönetilen iki akım
kayna÷ı yardımıyla gerçekleútirilebilece÷i kolayca görülebilir. Jiratörün bu úekilde
gerilimle yönetilen iki akım kayna÷ı ile gerçekleútiriliúi ùekil-2.20'da verilmiútir.
ùekil-2.20'daki yapı, iki INIC devresi ile gerçekleútirilebilir. Böyle bir devre ùekil2.21'de görülmektedir. Bu devre için dü÷üm denklemleri yazılırsa
P1 dü÷ümü için
V 3 -V 1 V 1
+ I1 = 0
Rg
Rg
(2.54)
ENDÜSTRøYEL ELEKTRONøK
34
V3
Rg
V4
Rg
+-
P1
Rg
Rg
N1
I1
N2
P2
I2
+
V2
-
+
V1
-
Rg
Rg
+ -
Rg
ùekil-2.21. øki INIC yardımıyla jiratör gerçekleútirilmesi.
N1 dü÷ümü için
V 3 -V 1 V 2 -V 1
+
=0
Rg
Rg
(2.55)
V 4 -V 2 V 1 -V 2
+
- I2 =0
Rg
Rg
(2.56)
V 4 -V 2 V 2
=0
Rg
Rg
(2.57)
P2 dü÷ümü için
N2 dü÷ümü için
ba÷ıntıları elde edilir. Bu ba÷ıntılarda V3 ve V4 gerilimlerinin elimine edilmesiyle
I1 =
I2 =
V2
(2.58)
Rg
V1
Rg
(2.59)
eúitlikleri elde edilir. Bu ba÷ıntılar ise jiratörün tanım ba÷ıntılarına özdeútirler.
LøNEER UYGULAMALAR
35
Jiratör uygulamaları
øúlemsel kuvvetlendiricilerle gerçekleútirilen jiratör devreleri çeúitli
uygulamalarda kullanılabilirler. Jiratörün 2 kapısına bir R2 direnci ba÷lansın.
Devrenin gerilim ve akımlarının yönleri uyarınca I2 = V2/Rg úeklindedir. Bu eúitlik
tanım ba÷ıntısına götürülürse
V 1 = I 2 . Rg =
V 2 . Rg
R2
2
V 1 Rg
R1 = =
I 1 R2
(2.60)
de÷erinde bir ohmik direnç elde edilir. Bu direnç 2 kapısına ba÷lanan R2 direncinin
tersi ile orantılıdır. Genel olarak, 1 kapısından görülen empedans Z1 ve 2 kapısına
ba÷lanan empedans Z2 ile gösterilirse, Z1 empedansı
Z1 =
R2g
Z2
(2.61)
olur. Bu da jiratörün ilginç bir uygulaması olarak kendini göstermektedir. 2
kapısına kapasitesi C2 olan bir kondansatör ba÷lansın. Bu durumda
Z2 =
1
jZC
olaca÷ından, 1 kapısından görülen empedans için
Z 1 = R 2g . j.Z . C 2
(2.62)
ba÷ıntısı bulunur. Bu ba÷ıntı uyarınca, bulunan büyüklük
L1 = R 2g . C 2
(2.63)
ENDÜSTRøYEL ELEKTRONøK
36
de÷erinde bir endüktansa karúı düúmektedir. Jiratörün bu uygulamasının sa÷ladı÷ı
baúlıca yarar, bu eleman yardımıyla büyük de÷erli ve düúük kayıplı endüktanslar
oluúturulabilmesidir.
C 2 = 1 PF , R g = 10k:
de÷erleri ile
L1 = 100H
de÷erinde endüktans de÷eri elde edilebilir. Alçak frekanslarda kullanılacak büyük
de÷erli endüktansları bu yoldan gerçekleútirmek mümkündür. Gerçekleútirilen
endüktansın kullanılma bölgesi, iúlemsel kuvvetlendiricinin çalıúma bölgesi ile
sınırlıdır.
L1 endüktansına bir C1 kondansatörünün paralel ba÷lanmasıyla bir paralel
rezonans devresi oluúturulabilir. Paralel rezonans devresinin de÷er katsayısı
açısından C1 = C2 alınması uygun olmaktadır.
Gerçek bir jiratör devresi ideal jiratöre göre farklılıklar gösterir. Jiratör
devresinin ideal jiratöre davranıúından sapmasının temel ölçüsü jiratör kayıplarıdır.
Gerçek jiratörün kayıpları eúde÷er devreye eklenen iki RV direnci ile gösterilir.
Kayıplı jiratörle oluúturulan paralel rezonans devresi ùekil-2.22'de verilmiútir.
Eúde÷er devrede kayıpları temsil eden büyüklük jiratörün de÷er katsayısı olarak
isimlendirilir. De÷er katsayısı
Q=
R1
2. R g
(2.64)
ba÷ıntısı ile belirlenir. Bu ba÷ıntı düsük frekanslarda geçerlidir. Jiratörün de÷er
katsayısı transfer karakteristi÷indeki akım ve gerilimler arasındaki faz kaymalarına
çok ba÷ımlıdır. De÷er katsayısı faz kaymasının fonksiyonu olarak
Q( M ) =
1
1
+M 1 + M 2
Q0
(2.65)
úeklinde ifade edilebilir. Bu ba÷ıntıdaki Q0 büyüklü÷ü alçak frekanslardaki de÷er
katsayısını, M1 ve M2 büyüklükleri ise I1 ve V2 ile I2 ve V1 arasında ve rezonans
frekansındaki faz kaymalarını göstermektedir. Faz gecikmesi oluúması durumunda
LøNEER UYGULAMALAR
37
rezonans frekansının yükseltilmesiyle Q de÷er katsayısı büyür. |M1 + M2| t 1/Q0
için devre kararsız olur. øleri faz durumunda ise rezonans frekansının arttırılması
ile Q deger katsayısı azalır.
I1
+V1
C1
Rg
I2
+V2
C2
RV
RV
+V1
2
Rg /R1
C
R
2
L=Rg .C
ùekil-2.22. Kayıplı jiratörle kurulan paralel rezonans devresi ve eúde÷eri.
øki uçlulara benzer úekilde jiratörler yardımıyla dört uçluları da çevirmek
mümkündür. Bunun için, çevrilecek dört uçlu iki jiratörün arasına ba÷lanır. Böyle
bir yapı ùekil-2.23'de verilmiútir. Yapıdaki dört uçlunun matrisi
§ A11
A ¨
© A21
A12 ·
¸
A22 ¹
(2.66)
ve her bir jiratörün tanım ba÷ıntısı da daha önce (2.53) ba÷ıntısıyla verilen biçimde
oldu÷una göre, yeni dört uçlu için elde edilecek matris
§ A22
A = A g . A. A g = ¨
2
© A12 / R g
A22 R g·
¸
A11 ¹
2
(2.67)
ENDÜSTRøYEL ELEKTRONøK
38
Rg
I1
Rg
+V1
I2
+V2
( A)
ùekil-2.23. Dört uçluların jiratör yardımıyla çevrilmesi.
(2.67) ba÷ıntısıyla verilmiútir. Dört uçluların jiratör yardımıyla çevrilmesine iliúkin
bir örnek ùekil-2.24 de verilmiútir.
Rg
Ca
I1
Cb
Rg
I2
+V2
+V1
Cc
L3
+V2
+V1
L1
L2
ùekil-2.24. Jiratörler yardımıyla dört uçluların çevrilmesine iliúkin bir örnek.
LøNEER UYGULAMALAR
39
ùekil-2.24’deki devre C lerden oluúan bir dört uçluyu L lerden oluúan bir
di÷er dört uçluya çevirmektedir. Çevirme sonucunda elde edilen yenidört uçlu da
úekil üzerinde gösterilmiútir. Yeni dort uçlunun elemanları
L1 = R 2g . C a , L2 = R 2g . Cb , L3 = R 2g . C c
úeklindedir. L1 ve L2 elemanlarına paralel birer kondansatör ba÷lanırsa, tümüyle
kondansatörlerden oluúan endüktif ba÷laúmalı band geçiren bir süzgeç kurulabilir.
Ca ve Cb elemanlarının kısadevre edilmeleri halinde ise, iki ucu topraktan yalıtılmıú
bir L3 endüktansı elde edilir. Bu tür uygulamalar, özellikle, büyük endüktanslı
bobinlerin gerçekleútirilmesinin zor oldu÷u alçak frekanslarda kullanılma açısından
elveriúli olmaktadır.
2.3. øntegral alıcılar
Endüstriyel elektronikte çeúitli uygulamalarda integral alıcılara sıkça
gereksinme duyulur. Bu uygulamalar arasında osilatör devreleri ve çeúitli türden
kontrol düzenleri sayılabilir. øntegral alıcılar, ço÷unlukla iúlemsel
kuvvetlendiriciler yardımıyla gerçekleútirilmektedir. Bu bölümde iúlemsel
kuvvetlendiriciler ile kurulan integral alıcılar ele alınacak, iúlemsel
kuvvetlendiricinin ideal olmamasının integral alıcının özelliklerinin idealden ne
derece sapmalara yol açaca÷ı incelenecektir. ødeal bir integral alıcı ile ideal
olmayan bir integral alıcı devresi ùekil-2.25'de verilmiútir. ødeal integral alıcı
devresindeki Z1 ve Z2 empedansları
R2
C2
R1
VI
R1
+
VO VI
C2
+
VO
KV(s)
ùekil-2.25.ødeal ve ideal olmayan integral alıcılar.
ENDÜSTRøYEL ELEKTRONøK
40
Z 1 = R1 , Z 2 =
1
sC 2
úeklindedir. Yine, ideal integratörde çıkıú gerilimi
VO = -
1
³ V I .dt + V(0)
TI
(2.68)
úeklinde ifade edilmektedir. Bu ba÷ıntıda TI =R1.C2 büyüklü÷ü devrenin zaman
sabitini, V(0) büyüklü÷ü ise çıkıú geriliminin ilk úartlarla belirlenen baúlangıç
de÷erini göstermektedir.
ødeal olmayan integral alıcının transfer fonksiyonu
KV (s). Z 2
Z 1 + Z 2 + KV (s). Z 1
KVf (s) =
(2.69)
úeklindedir. Burada KV(s) büyüklü÷ü iúlemsel kuvvetlendiricinin açık çevrim
transfer fonksiyonudur ve Z2 empedansı da
Z2 =
R2
1+ s. R 2 . C 2
(2.70)
biçimindedir. Ba÷ıntıdaki R2 direnci, integrasyon kondansatörünün kaçak direncini
göstermektedir.
Çıkıú geriliminin baúlangıç de÷erinin V(0) = 0 olması durumunda, devrenin çıkıú
gerilimi için
R2
1+ s. R2 .C2
V O = -V I
R2
R1 + R1 KV (s) 1+ s. R2 .C 2
KV (s)
(2.71)
ba÷ıntısı elde edilir. Bu ba÷ıntı düzenlenirse
VO =-
VI
s R1 C 2
1
1+
1
sR2 C 2
KV (s)
1+ KV (s)
1
1+
1
ª
1 º
sR1 C 2 (1+ KV (s))«1+
¬ sR2 C 2 »¼
bulunur. øúlemsel kuvvetlendiricinin açık çevrim kazancı
LøNEER UYGULAMALAR
KV (s) =
41
KVO
s
1+
ZO
ise, KVO >> 1 olması halinde, çıkıú gerilimi
VO = -
1
1
1
VI
s 1+ sT I
sT I 1+ 1 1+ 1
1+
Z O 1+ sKVO T I
sT C
sKVO TI
(2.72)
úeklinde yazılabilir. Ba÷ıntıdaki TI ve TC büyüklükleri, TI = R1.C2 ve TC = R2.C2
úeklinde tanımlanan zaman sabitleridir. (2.72) ba÷ıntısı dört bileúenin çarpımı
úeklindedir.
ølk terim
1
VO
=s. T I
VI
úeklindedir ve ideal integral alıcı transfer fonksiyonunu verir.
økinci terim integrasyon kondansatörünün kaçak akımlarına iliúkin hatayı
belirtmektedir.
Üçüncü terim, iúlemsel kuvvetlendiricinin açık çevrim kazancının sonlu
olmasından kaynaklanan bir terimdir.
Dördüncü terim ise yüksek frekans hatasını göstermekte ve iúlemsel
kuveetlendiricinin açık çevrim kazancının frekansa ba÷ımlı olmasının bir sonucu
olarak ortaya çıkmaktadır. ZTI >> 1 ve Z1 = Z0.KVO alınırsa, dördüncü terim
1
1
|
s
s 1+ sT I
1+
1+
Z O 1+ sKVO T I
Z1
olur.
T C «T I «T 1 , T C = R 2 . C 2 , T 1 =
1
Z1
úartı altında, integral alıcı geniú bir bölge içerisinde ideale yakın davranır. øntegral
alıcının frekans cevabı ùekil-2.26'da verilmiútir. ùekilden fark edilebilece÷i gibi,
ideal olmama nedeniyle frekans cevabında bir alçak frekans ve bir de yüksek
frekans hatası ortaya çıkmaktadır.
ENDÜSTRøYEL ELEKTRONøK
42
Devrenin ideal durumda zaman domenindeki cevabı
v O (t) = -V I
t
TI
úeklindedir. Alçak frekans hatası bu zaman domeni cevabını
v O (t) = -V I
t º
t ª
t º
T Cª
1 - exp(- )» | -V I «1 «
TI ¬
TC ¼
T I ¬ 2. T C »¼
(2.73)
biçimine dönüútürür.
VO/VI (dB)
ideal
Z0
alçak
frekans
hatası
kuvvetlendirici frekans e÷risi
1/TI
1/KVO.T I
1/T1 = Z 1
1/TC
log Z
yüksek frekans hatası
ùekil-2.26. ødeal olmayan integral alıcının frekans cevabı.
Alçak frekans hatası nedeniyle ortaya çıkacak ba÷ıl hata
' v O (t)
t
=2. T C
v O (t)
(2.74)
olur. Devrenin çıkıú geriliminin zamana ba÷lı de÷iúimi ùekil-2.27'da verilmiútir.
øntegrasyon kapasitesinin kaliteli bir eleman olması durumunda iúlemsel
kuvvetlendiricinin KVO açık çevrim kazancı yeteri kadar büyük de÷ilse, TC ve
KVO.TI aynı mertebede olurlar. Bu durumda, her iki zaman sabiti de alçak frekans
cevabını etkilerler. Buna göre, alçak frekans cevabı
LøNEER UYGULAMALAR
43
ideal
-vo(t)
(R2/R1).VI
-vo(t)
gerçek
ideal
gerçek
arctan(VI/TI)
t << TI
t >> TI
ùekil-2.27. Devrenin çıkıú geriliminin zamana ba÷lı de÷iúimi : a) t >> TI, b) t << TI
v O (t) = -V I
t ·
§ t ·º
T C . KVO ª §
¸ exp¨ - ¸ »
«exp¨ © TC¹ ¼
KVO . T I T C ¬ © KVO . T I ¹
(2.75)
úeklindedir. yeteri kadar küçük t süreleri için seri açılımı alınıp yüksek dereceden
terimler ihmal edilirse
1 ·º
VI ª t § 1
+ ¸»
v O (t) = - t«1- ¨
T I ¬ 2 © KVO .T I T C ¹¼
(2.76)
bulunur. Çıkıú geriliminde ortaya çıkacak ba÷ıl hata
' v O (t)
1·
t§ 1
+ ¸
=- ¨
2 © KVO . T I T C ¹
v O (t)
(2.77)
olur.
Yüksek frekans hatasının ideal basamak cevabına etkisi ele alınırsa,
devrenin basamak cevabı ideal durumdaki gibi
t
olaca÷ı yerde
TI
§
§ t ··º
VIª
v O (t) = - « t - T 1 ¨1- exp¨ - ¸¸»
© T 1 ¹¹¼
TI ¬
©
v O (t) = -V I
(2.78)
biçimini alır. Giriúe sinüs biçimli ve Z frekanslı bir iúaret uygulanırsa
V O (Z ) = -
V( Z )
jZ T I
1
Z
1+ j
Z1
(2.79)
olur. ødeal haldeki cevap ise
V O (Z ) = -
V I (Z )
jZ T I
(2.80)
ENDÜSTRøYEL ELEKTRONøK
44
úeklindedir. øki cevap arasındaki fark, genlik hatası ve faz hatası ile verilir.
Bunlardan genlik hatası
1§ Z ·
ha ( Z ) = - ¨ ¸
2© Z 1 ¹
2
(2.81)
faz hatası da
M ( Z ) = - arctan
Z
Z1
(2.82)
ba÷ıntısı ile verilmektedir.
Yüksek frekans hatası, R1 direncine paralel olarak kapasitesi C1 olan bir
kondansatör ba÷lanarak kompanze edilebilir. C1 kapasitesinin de÷eri
C1 =
1
TI
|
R1 .(1+ Z 1 . T I ) R1 .Z 1
(2.83)
ba÷ıntısından hareketle bulunabilir.
Teorik olarak, Z1 'in arttırılmasıyla yüksek frekans hatasının
azaltılabilece÷i söylenebilir. Ancak, integral yapısı içerisinde kullanıldıklarında,
iúlemsel kuvvetlendiriciler daima KVF = 1 durumunda kararlı kalacak úekilde
kompanze edilirler. Bu nedenle, birim kazanç band genıúli÷i düúük olur.
Dolayısıyla, integratör yapılarında yüksek frekans hatasını azaltmak üzere geniú
bandlı iúlemsel kuvvetlendiricilerin kullanılmasının yarar sa÷layaca÷ı açıktır.
øúlemsel kuvvetlendiriciden gelecek di÷er bir kısıtlama da, bu elemanın YE
yükselme e÷imi ve IO çıkıú akımından kaynaklanmaktadır. øntegral alıcının çıkıú
geriliminin maksimum de÷iúim hızı
dV O
dt
d
ma ks
I Omaks
C2
(2.84)
de÷erinden büyük olamaz.
Bunların yanısıra, gerçek iúlemsel kuvvetlendiricide giriú akımları ve
dengesizlik gerilimi sıfır de÷ildir. Bunlar, alçak frekans cevabına benzer bir hata
oluútururlar ve devrenin çıkıú gerilimi
v O (t) = (-V I r V IO + I 1 R1 )
§ t ··
t §
¨1 - exp¨ - ¸¸
© T C ¹¹
TI©
(2.85)
olur. I1 giriú akımının yönü, iúlemsel kuvvetlendirici yapısında kullanılan girıú
elemanının tipine ba÷lıdır. VIO dengesizlik gerilimi pozitif veya negatif olabilir. Bu
LøNEER UYGULAMALAR
45
hata, giriú sükunet akımı küçük olan iúlemsel kuvvetlendiriciler yahut düúük
dengesizlik gerilimli iúlemsel kuvvetlendiriciler kullanılarak azaltılabilir.
2.4. Türev alıcılar
øúlemsel kuvvetlendirici yardımıyla kurulan temel türev alma devresi
ùekil-2.28’de verilmiútir.
R2
C1
+
VI
VO
ùekil-2.28. øslemsel kuvvetlendirici ile kurulan türev alma devresi.
øúlemsel kuvvetlendiricinin ideal bir iúlemsel kuvvetlendirici olması durumunda
Z1 =
1
sC1
, Z 2 = R 2 , W d = R 2 . C1
olmak üzere, devrenin çıkıú gerilimi
v O (t) = - W d
dv I (t)
dt
(2.86)
ba÷ıntısıyla verilir. Pratikte, iúlemsel kuvvetlendiricinin ideal olmaması nedeniyle,
bu ba÷ıntı tam olarak sa÷lanamaz. Gerçek bir iúlemsel kuvvetlendiricide giriú
direnci sonludur; kazanç sonsuz de÷ildir ve yüksek frekanslara do÷ru gidildikçe
düúer. Bunların etkisiyle, yüksek frekanslarda iúlemsel kuvvetlendiricinin faz
kayması 180o dereceden büyük olur.
ENDÜSTRøYEL ELEKTRONøK
46
VO/VI (dB)
ideal
+20dB/dek
kuvvetlendirici frekans eðrisi
gerçek
log Z
çalýþma bölgesi
ùekil-2.29. Gerçek iúlemsel kuvvetlendirici ile kurulan türev alma devresinin çalıúma bölgesi.
Gerçek bir iúlemsel kuvvetlendirici ile kurulan türev alıcı devresinin
çalıúma bölgesi ùekil-2.29'da gösterilmiútir. ùekilde görülen ve +20 dB/dek'lık bir
e÷imle artan karakteristik, ideal devrenin davranıúını vermektedir. øúlemsel
kuvvetlendiricinin açık çevrim karakteristi÷i de úekil üzerinde gösterilmiútir. Fark
edilebilece÷i gibi, türev alma devresinin çalıúma bölgesi, bu iki karakteristi÷in
kesiúme noktası ile sınırlı olmaktadır. Çalıúma bölgesi sınırı iúlemsel
kuvvetlendiricinin frekans e÷risinin toleranslarına ba÷lıdır. Bu karakteristik C1
kondansatörüne seri bir R1 direnci ve R2 direncine paralel bir C2 kondansatörü
yardımıyla stabilize edilebilir. Z1 iúlemsel kuvvetlendiricinin birim kazanç band
geniúli÷ine karúı düúen açısal frekans olmak üzere, (1/R1.C2) < Z1 seçilir. Devre
yapısı ve elde edilecek karakakteristik ùekil-2.30'da verilmiútir. Devrenin çıkıú
gerilimi
V O (s) = -s. R2 . C1
1
1
VI
1+ s R1 C1 1+ s R2 C 2
(2.87)
olur. W = R1.C1 = R2.C2 alınırsa
V O = -s. R2 .C1
1
(1+ W .s )
2
(2.88)
VI
bulunur. Z << 1/W oldu÷u sürece, yapı ideal türev alma devresi gibi davranır. Baúka
bir deyiúle
V O | -s. R2 .C1 .V I , v O (t) = - W d
dv I
dt
(2.89)
LøNEER UYGULAMALAR
47
C2
C1
R1
R2
+
VI
VO
VO/VI (dB)
Z0
çalıúma bölgesi
1/R2C1
kuvvetlendirici frekans
e÷risi
1/ R1C1 R2C2
1/R1C2
log Z
ùekil-2.30. Türev alma devresi karakteristi÷inin stabilize edilmesi.
olur. Bu ba÷ıntılardan hareketle gerçek devrenin genlik ve faz hataları
hesaplanacak olursa, genlik hatası için
2
ha ( Z ) = -( Z .W )
(2.90)
eúitli÷i,faz hatası için de
M h ( Z ) = -2 arctan( Z .W )
ba÷ıntısı elde edilir.
(2.91)
ENDÜSTRøYEL ELEKTRONøK
48
2.5. øúlemsel kuvvetlendiricilerle kurulan özel sinüs osilatörü yapıları
øúlemsel kuvvetlendiricilerden yararlanılarak çesitli osilatör yapıları
gerçekleútirilebilir. Bunların arasında Wien osilatörü, çift-T osilatörü, iki fazlı
osilatör, analog hesaplayıcılı osilatör gibi sinüs osilatörleri, üçgen/karedalga
üreteçleri, darbe-boúluk oranı de÷iútirilebilen darbe üreteçleri, testerediúi (rampa)
üreteçleri gibi çeúitli türden dalga úekli üreteçleri sayılabilir. Bu bölümde, iúlemsel
kuvvetlendiricilerle kurulan ve çeúitli endüstriyel uygulamalarda kullanılmaya
elveriúli özel sinüs osilatörü yapıları ele alınarak incelenecektir. Di÷er dalga úekli
üreteçleri ise Bölüm-3’de ele alınacaktır.
øki fazlı osilatör
R1
C
R
C
R
+
+
OP1
P
R1 / 2
R
+
OP2
R
OP3
R
+V O
R
1
ùekil-2.31. øki fazlı osilatör
øki fazlı osilatör iki integral alıcı ve bir faz döndüren kuvvetlendiriciden
oluúan özel bir iúaret üreteci yapısıdır. Devrenin iki çıkıúı vardır ve bu iki çıkıúın
gerilimleri arasında 90o faz farkı bulunmaktadır. Bu nedenle, devre iki fazlı
osilatör olarak da isimlendirilmektedir. Devre, özellikle, alçak frekanslı sinüs
iúaretleri üretmeye elveriúlidir ve temel uygulama alanı alçak frekanslı ve kararlı
iúaretlerin (10-3...1 Hz) elde edilmesi olmaktadır. Sinüs salınımı, buna iliúkin
diferensiyel denklemin çözümü ile sa÷lanmaktadır. Dolayısıyla, devre analog
hesaplayıcılı osilatör ismiyle de anılmaktadır. øki fazlı osilatör devresi ùekil2.31'de görülmektedir. Devrenin standart iúlemsel kuvvetlendirici yapılarıyla
kuruldu÷u düúünülecek olursa, alçak frekanslarda her bir iúlemsel
kuvvetlendiricinin açık çevrim kazancı KV(s) = KV0 olur.
LøNEER UYGULAMALAR
49
Devredeki integral alıcılar için transfer fonksiyonu
KVf 2 (s) =
KV 0
1+ sRC(1+ KV 0 )
faz döndüren kuvvetlendiricisinin transfer fonksiyonu da
KVf 1 (s) = -
D . KV 0
| -D
1+ D + KV 0
úeklindedir. Faz döndüren kuvvetlendiricinin giriúinden çıkıúa transfer fonksiyonu
yazılırsa
T(s) =
Db K V 0
D KV 0
2
(2.92)
1+ sRC(1+ KV 0 ) [1+ s RC(1+ KV 0 )] 2
elde edilir. Devrenin osilasyon yapabilmesi için gereken faz ve genlik úartları
ZRC(1+ KV 0 )(2 - Db KV 0 ) = 0
(2.93)
1+ D KV 0 - Db KV 0 - Z 2 R2 C 2 (1+ KV 0 ) = 0
2
2
(2.94)
úeklindedir. Bunu sa÷layan b de÷eri ise
b=
2
D KV 0
(2.95)
ba÷ıntısıyla belirlenir. Bu büyüklük (2.94) ba÷ıntısında yerine konursa, osilasyon
frekansı için
1 D KV 0 - 1
Z0 =
RC ( KV 0 +1)
2
bulunur.
D = 1 , KV 0 «1
(2.96)
ENDÜSTRøYEL ELEKTRONøK
50
olması durumunda
b=
2
1
, Z0 =
RC
KV0
((2.97)
eúitlikleri elde edilir. Devredeki Zener diyotları, osilasyon genli÷ini sınırlamak
amacıyla kullanılmıútır.
Analog hesaplayıcılı osilatör
R
C
V1
R
V2
C
R1
R1
+VO
+
+
OP1
+
OP2
OP3
P
D VO
10R
ùekil-2.32. Analog hesaplayıcılı sinüs osilatörü
øki fazlı osilatör yapısıyla aynı ilkeye dayanan bir çalıúma biçimi gösteren
analog hesaplayıcılı osilatör, özellikle alçak frekanslı sinüs iúaretleri üretmeye
yönelik olarak kullanılan bir devre düzenidir. Devrenin çalıúması, sinüs salınımına
iliúkin diferensiyel denklemin çözülmesine dayanır. Bu nedenle, yapı, analog
hesaplayıcılı osilatör olarak da isimlendirilmektedir. Çözülmesi gereken
diferensiyel denklem
V O "+2J V O '+Z O V O = 0
2
(2.98)
biçiminde bir diferensiyel denklemdir ve bunun çözümü de
v o (t) = V OM exp(-Jt). sin Z o - J .t
2
2
(2.99)
LøNEER UYGULAMALAR
51
úeklinde olur. Diferensiyel denklemin çözümü iúlemsel kuvvetlendiricilerle kurulan
devreler yardımıyla integral alınarak elde edilebilir. Bu yapılırsa
V O + 2J ³V O dt+Z o ³ ³V O dt 2= 0
2
(2.100)
denklemi elde edilir. Bu denklem iki integral alıcı ve bir faz döndüren
kuvvetlendirici yardımıyla gerçekleútirilebilir. Devre yapısı ùekil-2.32'da
görülmektedir.
Devrenin sönüm katsayısı J = -D/20RC ve rezonans frekansı da fO =1/2SRC
úeklindedir. Buna göre çözüm
· §
§ D
D2 t ·
¸
t ¸. sin¨ 1v o (t) = V OM .exp¨
© 20RC ¹ ©
400 RC ¹
(2.101)
olur. D büyüklü÷ü ile zayıflama ayarlanır. D büyüklü÷üne -1 < D < 1 de÷erleri
arasında herhangi bir de÷er verilebilir. P potansiyometresinin orta konumunda D =
0 olur. D=1 durumunda, baúlangıçtan itibaren 20 periyot geçtikten sonra çıkıú
iúaretinin genli÷i e katına ulaúır. D = -1 için ise, aynı süre sonunda genlik
baúlangıçtaki de÷erinin 1/e katı bir de÷er alır. D= 0 zayıflatmasız, baúka bir deyiúle
sönümsüz bir salınım elde edilir. Ancak, salınımı baúlatabilmek için D > 0 olması
gerekmektedir.
Bunu sa÷layabilmek üzere, genli÷in her an ölcülüp
de÷erlendirildi÷i bir genlik kontrolu düzeni gerekli olur. Böyle bir genlik kontrolü
düzeni, devrenin özelliklerinden yararlanılarak kolayca geçekleútirilebilir.
Devredeki gerilimler ele alınırsa, sönümsüz titreúim durumunda
V O = V OM .sinZt ve V 1 = -
1
W
³V O dt= -V OM . cosZt
olur. Genli÷in belirlenmesi iúlevi
V O +V 1 =V OM ( sin2Zt+ cos2Zt ) =V OM
2
2
2
2
ba÷ıntısı yardımıyla kolayca gerçekleútirilebilir. Fark edilebilece÷i gibi, VO2 + V12
terimi salınımın fazına de÷il, sadece genli÷ine ba÷lıdır. Bu durumda söz konusu
terim için saf bir do÷ru gerilim elde edilir ve herhangi bir alçak geçiren süzgece
gerek duyulmaz. Elde edilen bu do÷ru gerilimin bir referans gerilimi ile
ENDÜSTRøYEL ELEKTRONøK
52
karúılaútırılmasıyla da genlik kontrolu iúlevi sa÷lanabilir. Böyle bir devre düzeni
ùekil-2.33'de verilmiútir. Bu devrede V3 gerilimi
2
2
V1
V O V ref
+
=0
E R2 E R2 R2
R
C
R
+
R1
R1
C
+
+
OP1
OP2
10R
2
V
__1
E
+VO
OP3
V 3 . VO
______
E
R2
M3
R2
C1
M1
2
VO
__
E
R3
+V
M2
R2
3
+
-V ref
ùekil-2.33. Analog hesaplayıcılı osilatörde genlik kontrolu.
olacak úekilde ayarlanmaktadır. Bu durumda
V 2OM = E.V Ref
olur. R3C1 çarpımı ile kuvvetlendiricinin zaman sabiti belirlenir. M3 çarpma
devresinin çıkıúından VO.V3/E de÷erinde bir gerilim elde edilir. Devrede M3
çarpma devresi potansiyometre yerine kullanılmaktadır. Böylece D = V3/E olur.
Genli÷in herhangi bir nedenle artması durumunda VO2 > E.Vref elde edilir. Bununla
V3 gerilimi, dolayısıyla da D büyüklü÷ü negatif olur ve genlik zayıflatılır. Genli÷in
herhangi bir nedenle azalması durumunda ise V3 gerilimi pozitif de÷erler alır ve
önceki durumun tersi ortaya çıkar. Bütün bunlara bakılacak olursa, devrede etkin
bir genlik kontrolu oluúaca÷ı kolayca söylenebilir.
LøNEER UYGULAMALAR
53
KAYNAKLAR
[1]
[2]
[3]
[4]
[5]
[6]
[7]
[8]
[9]
[10]
[11]
SIMPSON, C.D., Industrial electronics, Prentice Hall, Englewood
Cliffs, 1996.
HUMPHRIES, J., and SHEETS, L. P., Industrial Electronics, Breton
Publishers, 1983.
GREBENE, A.B., Bipolar and MOS analog integrated circuit design,
John Wiley and Sons Inc., New York, 1984.
TIETZE, U. and SCHENK, Ch., Halbleiterschaltungstechnik,
Springer Verlag, 1983.
HERPY, M., Analog integrated circuits, John Wiley and Sons, 1980.
TIETZE, U. and SCHENK, Ch., Advanced electronic circuits ,
Springer Verlag, 1978.
STANLEY, W.D., Operational amplifiers with linear integrated
circuits, Merrill Publishing Company, 1989.
REGTIEN, P.P.L., Instrumentation electronics, Prentice Hall,
Englewood Cliffs, 1992.
ALLEN, P.E. and HOLBERG,D.R., CMOS analog circuit design,
Holt-Rinehart and Winston Inc. 1987.
KUNTMAN, H., Analog tümdevre tasarımı, Sistem yayınları, 1992.
HELFRICK, A.D. and COOPER, W.D., Modern Electronic
Instrumentation and measurement techniques, Prentice Hall, 1990.