T.C. SAKARYA ÜNİVERSİTESİ MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ
DİFERANSİYEL DERSİ 2015-GÜZ ARA SINAVI
(Doç.Dr. Ekrem BÜYÜKKAYA- Yrd.Doç.Dr. Ünal UYSAL- Yrd.Doç.Dr. Hüseyin DAL -Yrd.Doç.Dr. Zekeriya PARLAK)
Açıklamalar: Süre 75 dakikadır. Her soru eşit ağırlıktadır. Değerlendirmede okunaklı olmayan ve/veya birbiri içerisine karışmış, sistematik
bir yaklaşımın olmadığı anlaşılan çözümler dikkate alınmayacaktır. Sonucu doğru ancak gidiş yolu hatalı ve/veya eksik çözümler kopya olarak
değerlendirilecektir. Kâğıda cevap olarak yazdığınız ancak çözümden uzak olan yanıtlarınızın mutlaka bir puan karşılığı yoktur. Sınav
esnasında her türden malzeme alışverişi yasaktır. Kopya çeken ve kopya çekilmesine göz yuman aynı derecede sorumlu tutulacaktır. Sınav
esnasısın her ne sebeple olursa olsun cep telefonu kullanmak yasaktır. Cep telefonları kapalı tutulacaktır, kapalı tutmayanların sınavları iptal
edilecektir.
SORU #1 𝒙𝟐 𝒚′′ + 𝟑𝒙𝒚′ − 𝟑𝒚 = 𝒙 diferansiyel denkleminin genel çözümünü bulunuz. 25P
𝒚
SORU #2 𝒙𝒆𝒙 + 𝒚 − 𝒙𝒚′ = 𝟎 diferansiyel denklemini çözünüz. 25P
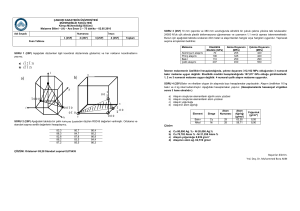
SORU #3 SORU #3 Aşağıdaki şekilde verildiği gibi, sürtünmesiz bir zemin üzerinde duran 1
kg’lık m kütleli bir cisim, duvara sönüm elemanı (𝒓) ile bağlanmış ve kütleye 𝑭𝟎 kuvveti
etkimektedir. Başlangıç anında hareketsiz olan kütlenin hızını zamana (𝒕) bağlı olarak elde
ediniz. 25P
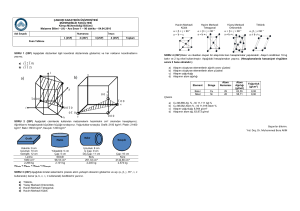
SORU #4 Kütlesi 𝒎 olan bir silindir iç yüzeyleri ℎ kalınlığında
bir yağ ile kaplı düşey bir borudan aşağı doğru kaymaya
bırakılmaktadır. Silindirin çapı 𝑫, yüksekliği ise 𝑳 olarak
verilmektedir. Bu sistemde, silindirin ağırlığından kaynaklanan
kuvveti (𝑭𝑨 = 𝒎𝒈) ve bunun ters yönünde silindirin yanal
yüzeyi ile borunun iç yüzeyi arasındaki yağdan kaynaklanan
𝜇𝜋𝐷𝐿
sürtünme kuvveti (𝑭𝒔 = 𝒌𝑽) vardır. Burada 𝑘 = ℎ ile
hesaplanan sabit bir katsayıdır. Newton’un ikinci yasası gereği
𝒅𝑽
bu silindir üzerindeki toplam kuvvet; 𝑭 = 𝒎𝒂 = 𝒎 𝒅𝒕 ile
verilmektedir. Başlangıç anında hareketsiz olan silindirin
konumunun, zamana göre fonksiyonu olan, 𝒚(𝒕) bağıntısını
geliştiriniz. (Aşağı yönü pozitif alınız) 25P
y
Her soru eşit puandır.
Başarılar…
CEVAP #1
2. I.Yol
𝑦
𝑦′ = 𝑒𝑥 +
𝑦
𝑥
ş𝑒𝑘𝑙𝑖𝑛𝑑𝑒 𝑦𝑎𝑧𝚤𝑙𝑎𝑏𝑖𝑙𝑖𝑟.
𝑦 = 𝑢𝑥 𝑑ö𝑛üşü𝑚ü 𝑦𝑎𝑝𝚤𝑙𝚤𝑟𝑠𝑎
𝑦′ =
𝑑𝑦
𝑑𝑢
=𝑥
+𝑢
𝑑𝑥
𝑑𝑥
𝑢=
𝑦
ş𝑒𝑘𝑙𝑖𝑛𝑑𝑒 𝑑𝑒 𝑦𝑎𝑧𝚤𝑙𝑎𝑏𝑖𝑙𝑖𝑟,
𝑥
ş𝑒𝑘𝑙𝑖𝑛𝑑𝑒 𝑜𝑙𝑎𝑐𝑎𝑘𝑡𝚤𝑟.
Denklemde dönüşümler yerine yazılırsa;
𝑥
𝑑𝑦
+ 𝑢 = 𝑒𝑢 + 𝑢
𝑑𝑥
𝑑𝑢 𝑑𝑥
=
𝑒𝑢
𝑥
𝑑𝑖𝑓𝑒𝑟𝑎𝑛𝑠𝑖𝑦𝑒𝑙 𝑑𝑒𝑛𝑘𝑙𝑒𝑚 𝑒𝑙𝑑𝑒 𝑒𝑑𝑖𝑙𝑖𝑟,
⟹
−𝑒 −𝑢 = 𝑙𝑛𝑥 + 𝑙𝑛𝐶 𝑏𝑢𝑙𝑢𝑛𝑢𝑟, 𝑡𝑒𝑟𝑠 𝑑ö𝑛üşü𝑚 𝑦𝑎𝑝𝚤𝑙𝚤𝑟𝑠𝑎;
𝑦
−𝑒 −𝑥 = 𝑙𝑛𝐶𝑥 𝑏𝑢𝑙𝑢𝑛𝑢𝑟.
II.Yol
𝑦
𝑥 𝑒 𝑥 + 𝑦 − 𝑥𝑦 ′ = 0
𝑦 = 𝑢𝑥 𝑑ö𝑛üşü𝑚ü 𝑦𝑎𝑝𝚤𝑙𝚤𝑟𝑠𝑎,
𝑑𝑦 = 𝑥 𝑑𝑢 + 𝑢 𝑑𝑥 ş𝑒𝑘𝑙𝑖𝑛𝑑𝑒 𝑜𝑙𝑎𝑐𝑎𝑘𝑡𝚤𝑟.
(𝑥 𝑒 𝑢 + 𝑢𝑥)𝑑𝑥 − 𝑥(𝑥𝑑𝑢 + 𝑢𝑑𝑥) = 0
𝑥 𝑒 𝑢 𝑑𝑥 + 𝑢𝑥𝑑𝑥 − 𝑥 2 𝑑𝑢 − 𝑥𝑢𝑑𝑥 = 0
𝑥 𝑒 𝑢 𝑑𝑥 − 𝑥 2 𝑑𝑢 = 0
1
𝑑𝑢
𝑑𝑥 − 𝑢 = 0 𝑖𝑛𝑡𝑒𝑔𝑟𝑎𝑙 𝑎𝑙𝚤𝑛𝚤𝑟𝑠𝑎
𝑥
𝑒
𝑙𝑛𝑥 − 𝑒 −𝑢 = 𝑙𝑛𝐶 𝑡𝑒𝑟𝑠 𝑑ö𝑛üşü𝑚 𝑦𝑎𝑝𝚤𝑙𝚤𝑟𝑠𝑎;
𝑦
−𝑒 −𝑥 = 𝑙𝑛𝑥 − 𝑙𝑛𝐶 𝑏𝑢𝑙𝑢𝑛𝑢𝑟.
3.
𝑚𝑎 = −𝑟𝑥̇ + 𝐹0
𝑚𝑥̈ + 𝑟𝑥̇ = 𝐹0
𝑥̈ + 𝑟𝑥̇ = 𝐹0
𝑑2𝑥
𝑑𝑥
+
𝑟
= 𝐹0
𝑑𝑡 2
𝑑𝑡
𝑑 𝑑𝑥
𝑑𝑥
+𝑟
= 𝐹0
𝑑𝑡 𝑑𝑡
𝑑𝑡
𝑑
𝑣(𝑡) + 𝑟𝑣(𝑡) = 𝐹0
𝑑𝑡
𝑣̇ (𝑡) + 𝑟𝑣(𝑡) = 𝐹0
𝑣̇ + 𝑟𝑣 = 𝐹0
𝑦 ′ + 𝑃(𝑡)𝑦 = 𝑅(𝑡)
→
𝑃(𝑡) = 𝑟 ,
𝑅(𝑡) = 𝐹0
𝜇(𝑡) = 𝑒 ∫ 𝑃(𝑡)𝑑𝑡 = 𝑒 ∫ 𝑟 𝑑𝑡 = 𝑒 𝑟𝑡
𝑣(𝑡) =
1
[∫ 𝜇(𝑡)𝑅(𝑡)𝑑𝑡 + 𝐶]
𝜇(𝑡)
𝑣(𝑡) =
1
[∫ 𝑒 𝑟𝑡 𝐹0 𝑑𝑡 + 𝐶]
𝑒 𝑟𝑡
𝑣(𝑡) = 𝑒 −𝑟𝑡 [𝐹0
𝑣(𝑡) =
𝑒 𝑟𝑡
+ 𝐶]
𝑟
𝐹0
+ 𝐶𝑒 −𝑟𝑡
𝑟
𝑣(𝑡) = 𝐶𝑒 −𝑟𝑡 −
𝐹0
𝑟
→
Genel çözüm
Başlangıç anında (𝑡 = 0) hareketsiz olduğu için başlangıç hızı sıfır (𝑣 = 0) olur.
𝑣(0) = 0
𝒗(𝒕) =
→
𝑣(0) = 𝐶𝑒 −𝑟0 −
𝑭𝟎 −𝒓𝒕 𝑭𝟎
𝒆 −
𝒓
𝒓
→
𝐹0
=0
𝑟
veya
→
→
𝐶=
𝐹0
𝑟
𝒗(𝒕) =
𝑭𝟎 −𝒓𝒕
(𝒆 − 𝟏)
𝒓
4. a)
𝐹 = 𝐹𝐴 + 𝐹𝑠
𝑚
𝑑𝑉
= 𝑚𝑔 − 𝑘𝑉
𝑑𝑡
𝑑𝑉 𝑘
+ 𝑉=𝑔
𝑑𝑡 𝑚
Bu birinci mertebeden lineer diferansiyel denklemdir.
𝑦 ′ + 𝑃(𝑥)𝑦 = 𝑅(𝑥)
𝑘
𝑘
𝜇(𝑡) = 𝑒 ∫ 𝑃(𝑡)𝑑𝑡 = 𝑒 ∫𝑚𝑑𝑡 = 𝑒 𝑚𝑡
𝑉(𝑡) =
𝑉(𝑡) =
1
[∫ 𝜇(𝑡)𝑅(𝑡)𝑑𝑡 + 𝐶]
𝜇(𝑡)
1
𝑘
𝑘
𝑒 𝑚𝑡
𝑘
[∫ 𝑒 𝑚𝑡 𝑔𝑑𝑡 + 𝐶]
𝑉(𝑡) = 𝑒 −𝑚𝑡 [
𝑉(𝑡) =
𝑚𝑔 𝑘 𝑡
𝑒 𝑚 + 𝐶]
𝑘
𝑘
𝑚𝑔
+ 𝐶𝑒 −𝑚𝑡
𝑘
𝑉(0) = 0 başlangıç değerine göre
𝐶=−
𝑚𝑔
𝑘
𝑉(𝑡) =
𝑘
𝑚𝑔
(1 − 𝑒 −𝑚𝑡 )
𝑘
b)
𝑡 → ∞ için
𝑉(𝑡) =
𝑚𝑔
𝑘
limit hız değerine ulaşır.