PowerPoint Sunusu

ÜÇGENLER
1.Üçgenlar
2.Dik Kenarlar
3.Yükseklik
4.Hipotenüs
İÇİNDEKİLER:
5.Pisagor Bağıntısı
6.Üçgen Eşitsizliği
7.Kenarortay
8.Açıortay
Kazanımlar
1.ÜÇGENLER:
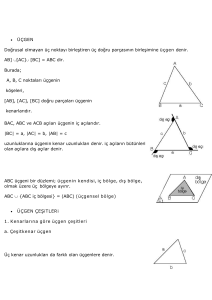
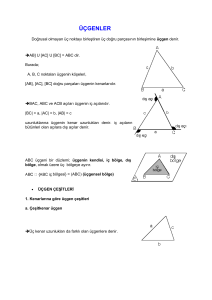
 Doğrusal olmayan üç noktayı birleştiren doğru parçalarının meydana getirdiği şekle üçgen denir.
 Köşeleri: A, B ve C
 Kenarları: [Ab], [BC] ve [AC]
 Kenar Uzunlukları: A, B ve C
2.DIK KENARLAR:
 Bir açısının ölçüsü 90 derece olan üçgene dik üçgen denir.
 Dik üçgende 90 derecelik kenarlara dik kenarlar denir.
 |AB| |BC| dik kenarlardır.
3.YÜKSEKLİK:
 Bir taban ve tepeden tabana indirilen bir dikme.
 h ile gösterilir.
4.HIPOTENÜS:
 90 derecelik açının karşısındaki kenara hipotenüs denir.
 Hipotenüs en uzun kenardır.
 |AB| < |AC|
 |BC|< |AC|
5.PİSAGOR BAĞINTISI:
 Hipootenüsü bulmak için geliştirilmiş bir teoremdir.
 Pisagor bağıntısında bilinmesi gereken bazı özel üçgenler vardır.Bunladan bazıları:
 3-4-5
 5-12-13
 8-15-17
 7-24-25
 .....
6.ÜÇGEN EŞİTSİZLİĞİ:
 Bir üçgende bir kenarın uzunluğu diğer iki kenarın uzunlukları toplamından küçük, farkının mutlak
değerinden büyüktür. Bu eşitsizliğe üçgen eşitsizliği denir.
 a + b > c > |a−b|
 a + c > b > |a−c|
 b + c > a > |b−c|
7.KENARORTAY:
• 1. AĞIRLIK MERKEZI:
 Üçgenlerde kenarortaylar bir noktada kesişirler
 Kenarortayların kesişim noktasına ağırlık merkezi denir.
 ABC üçgeninde [AD], [BE] ve [CF]
kenarortaylarının kesiştikleri G noktasına
ABC üçgeninin ağırlık merkezi denir.
 Ağırlık merkezi kenarortayı, kenara 1 birim, köşeye 2 birim olacak şekilde böler.
 ABC üçgeninde D, E, F noktaları bulundukları kenarların orta noktaları ve G ağırlık merkezi ise;
|BG|=2.|GE|
|AG|=2|GD|
|CG|=2.|GF|
 Bir üçgende iki kenarortayın kesişmesiyle oluşan nokta ağırlık merkezidir.
 ABC üçgeninde [AD] kenarortay ve AG = 2GD olduğundan G noktası
ağırlık merkezidir.
 ABC üçgeninde [AD] kenarortay ve CG = 2FG olduğundan G noktası ağırlık
merkezidir.
 ABC üçgeninde AG = 2GD ve CG = 2GF eşitliğini sağlayan G noktası ABC üçgeninin
ağırlık merkezidir.
2.KENARORTAY UZUNLUĞU:
bir üçgende kenarortayın uzunluğunu bulmak için;
bağıntısı kullanılır.Eğer tüm kenarortaylar için bu eşitlik yazılır ve taraf tarafa toplanırsa şu eşitlik
elde edilir:
3.DİK ÜÇGENDE KENARORTAY:
 Muhteşem üçlü:Bir dik üçgende A noktasından hipotenüse ait çizilen kenarortay doğru parçası
hipotenüsün yarısına eşittir.
 Bir dik üçgende dik kenarlara ait kenarortaylarının karelerinin toplamı hipotenüse ait kenarortayın
karesinin beş katıdır:
8.AÇIORTAY:
 Geometride bir açıyı iki eşit açı şeklinde bölen yapıdır.
 Bir açıya teğet tüm çemberler çizilerek merkezleri birleştirilirse, o açının açıortayı elde edilir.
1.İÇ AÇIORTAY TEOREMİ:
[AN] açıortay doğrusu olmak üzere;
2.DIŞ AÇIORTAY TEOREMİ:
[AN] dış açıortay doğrusu olmak üzere;
3.İÇ AÇIORTAY TEOREMİ:
[AN] açıortay doğrusu olmak üzere;
4.DIŞ AÇIORTAY TEOREMİ:
[AN] açıortay doğrusu olmak üzere;
HADI BIRAZ SORU ÇÖZELIM
CEVAP:D
CEVAP:C
CEVAP:B
KAZANIMLAR:
 8.3.1.1. Üçgende kenarortay, açıortay ve yüksekliği inşa eder.
 8.3.1.2. Üçgenin iki kenar uzunluğunun toplamı veya farkı ile üçüncü kenarının uzunluğunu
ilişkilendirir.
 8.3.1.3. Üçgenin kenar uzunlukları ile bu kenarların karşısındaki açıların ölçülerini ilişkilendirir.
 8.3.1.4. Yeterli sayıda elemanının ölçüleri verilen bir üçgeni çizer.
 8.3.1.5. Pisagor bağıntısını oluşturur; ilgili problemleri çözer.
BENI DINLEDIĞINIZ IÇIN TEŞEKKÜR EDERIM
BETÜL ÖZTÜRK
2-B
140403072
