Matematik Bölümü Diferansiyel Denklemler I

Analiz II
Çalışma Soruları-3
Son güncelleme: 14.04.2011
..
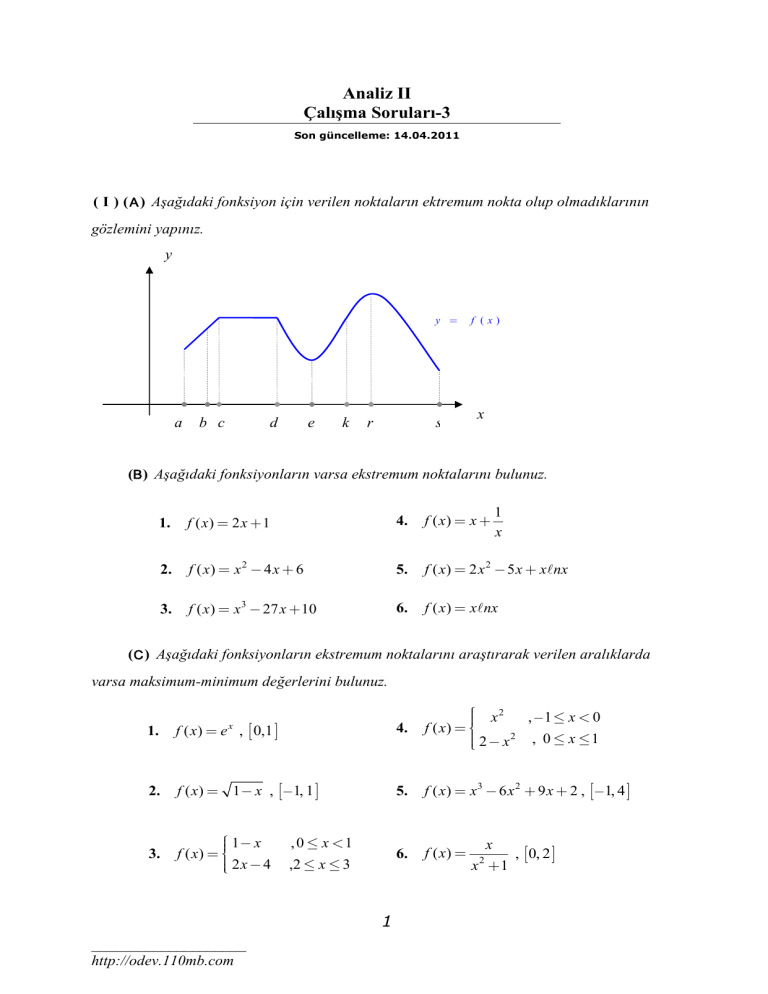
( I ) ( A ) Aşağıdaki fonksiyon için verilen noktaların ektremum nokta olup olmadıklarının
gözlemini yapınız.
y
y =
a
b c
d
e
k
r
s
f (x)
x
(B ) Aşağıdaki fonksiyonların varsa ekstremum noktalarını bulunuz.
1
x
1.
f ( x) = 2 x + 1
4.
f ( x) = x +
2.
f ( x) = x 2 − 4 x + 6
5.
f ( x ) = 2 x 2 − 5 x + xAnx
3.
f ( x) = x3 − 27 x + 10
6.
f ( x ) = xA n x
(C ) Aşağıdaki fonksiyonların ekstremum noktalarını araştırarak verilen aralıklarda
varsa maksimum-minimum değerlerini bulunuz.
4.
⎧⎪ .x 2
, −1 ≤ x < 0
f ( x) = ⎪⎨
⎪⎪.2 − x 2 ,..0 ≤ x ≤ 1...
⎩
f ( x ) = 1− x , [−1, 1 ]
5.
f ( x ) = x 3 − 6 x 2 + 9 x + 2 , [−1, 4 ]
, 0 ≤ x <1
⎪⎧.1− x
f ( x) = ⎪⎨
⎪⎪⎩.2 x − 4. ,2 ≤ x ≤ 3..
6.
f ( x) =
1.
f ( x ) = e , [ 0,1 ]
2.
3.
x
.
.
.
.
.
1
____________________
http://odev.110mb.com
.
x
, [0, 2 ]
x +1
2
.
.
.
(.II.) Aşağıdaki fonksiyonların grafiklerini çiziniz.
1
x
1.
f ( x) = x 4 − 8 x 2
5.
f ( x) = x −
2.
f ( x) = x 4 − 6 x 2
6.
f ( x) =
x
x −1
3.
f ( x) =
7.
f ( x) =
x2
x 2 −1
4.
f ( x ) = x 2 − x + 12
x2
x2 + 3
2
____________________
http://odev.110mb.com
Not: Yanıtlar-Yol göstermeler kontrol amaçlıdır, yazım hatası - eksiklikler vs.. olabilir..
kendi çözümlerinizle mutlaka karşılaştırınız..
Çalışma Soruları-3 (son güncelleme : 14.04.2011)
Yanıtlar - Yol Göstermeler I
Önbilgi 1. D ⊆ \ , f : D → \ fonksiyonu, x0 ∈ D noktası, U : x0 ın bir civarı ( U ⊆ D )
.
.
.
.
verilsin. EN: Yerel Ekstremum (maksimum-minimum) nokta, KN: Kritik nokta, y: Yerel,
m:Mutlak.
x0 y.minimum : “ ∀x ∈ U için f ( x) ≥ f ( x0 ) ”
..
.
x0 y.maksimum : “ ∀x ∈ U için f ( x) ≤ f ( x0 ) ”
..
.
Not 1: Yukarıdaki tanımlarda U yerine D alınırsa sırasıyla m.minimum-m.maksimum tanımları elde edilir.
Başka ifade ile m.maksimum (m.minimum): y.maksimum noktalarının en büyüğü(en küçüğü)dür.
(KN.ların tespiti) KN.lar: f ′( x0 ) = 0 şeklindeki x0 noktaları.
(EN için bir gerek koşul) x0 EN ⇒ x0 KN.
Not 2: Bu sonuç türevin varlığı hipotezi altında geçerlidir. O halde x0 da türev var ve x0 KN değil ise x0 EN
değildir.
(KN.larda EN araştırması) x0 KN olsun.
..
( i ) (Birinci Türevin işaretinin incelenmesi)
x
x0
f ′( x )
+
−
f ( x)
y .m a k s im u m
x
x0
f ′( x )
−
+
f ( x)
y .m in im u m
Not 3: Diğer durumlarda x0 EN değildir diyebiliriz.
____________________
http://odev.110mb.com
1
(.ii.) (İkinci Türev Testi) (EN için bir yeter koşul)
“ f ′′( x0 ) > 0 ⇒ x0 y.minimum” , “ f ′′( x0 ) < 0 ⇒ x0 y.maksimum”.
Not 4: Bu sonuç ikinci türevin varlığı hipotezi altında geçerlidir. Testin sonuç vermediği durumlar için x0 EN
değildir diyemeyiz.
A. c , d , r : y.maksimum; r : m.maksimum; e : y.minimum; s : m.minimum;
a , b , k : EN değil.
B1. f ( x ) = 2 x + 1 ⇒ f ′( x) = 2 ⇒ KN yok
.
⇒
N
EN yok !
Not 2 den
⎧⎪
⎪⎪ f ′( x) = 2 x − 4 = 0
⎪
B2. f ( x ) = x 2 − 4 x + 6 ⇒ f ′( x) = 2 x − 4 , KN. : ⎪⎨
⇓
⎪⎪
x=2
⎪⎪
⎪⎩
x
2
f ′( x )
+
−
f ( x)
y .m in im u m
⎧⎪
⎪⎪ f ′( x) = 3( x − 3)( x + 3) = 0
⎪
3
2
B3. f ( x) = x − 27 x + 10 ⇒ f ′( x ) = 3 x − 27 , KN. : ⎪⎨
⇓
⎪⎪
x1 = −3, .x2 = 3
⎪⎪
⎪⎩
−3
x
f ′( x )
+
3
−
+
f ( x)
y .m a k s im u m
2
____________________
http://odev.110mb.com
y .m in im u m
⎛ 1 ⎞⎛ 1 ⎞
⎧
f ′( x) = ⎜⎜1− ⎟⎟⎟⎜⎜1 + ⎟⎟⎟ = 0
⎪
⎪
⎝⎜ x ⎠⎝⎜ x ⎠
⎪
⎪
1
1
⇓
B4. f ( x) = x + ⇒ f ′( x) = 1− 2 , KN. : ⎪
⎨
⎪
x
x
⎪
x1 = −1, .x2 = 1
⎪
⎪
⎪
⎩
x
−1
f ′( x )
1
+
+
−
f ( x)
y .m a k s im u m
y .m in im u m
⎧
⎪
⎪⎪ f ′( x) = 4 x − 4 + Anx = 0
⎪
⇓
B5. f ( x ) = 2 x 2 − 5 x + xAnx ⇒ f ′( x) = 4 x − 4 + Anx , KN. : ⎪
⎨
⎪
⎪
x =1
⎪
⎪
⎪
⎩
⇒ f ′′( x) = 4 +
1
⇒ f ′′(1) = 5 > 0
x
.
x = 1 y.minimum.
⇒
N
.
ikinci türev testinden
⎧
⎪
⎪⎪⎪ f ′( x) = 1 + Anx = 0 ⇒ Anx = −1
⇓
B6. f ( x ) = xAnx ⇒ f ′( x) = 1 + Anx , KN. : ⎪⎨
⎪⎪
1
⎪⎪
x=
⎪⎩
e
⇒ f ′′( x) =
1
1
⇒ f ′′( ) = e > 0
x
e
.
.
x=
⇒
N
ikinci türev testinden
3
____________________
http://odev.110mb.com
1
y.minimum.
e
Grafikler (gözlem için):
C1. f ( x ) = e x , [ 0,1 ] ⇒ f ′( x ) = e x ⇒ KN yok
.
.
.
⇒
N
Aralığın iç noktalarında EN
Not 2 den
yok !. Uç noktaları inceleyelim: f ′( x ) = e x > 0 ⇒ f Artan ⇒ x = 0 m.minimum, x = 1
.
m.maksimum ⇒ Minimum değer: f (0) = 1 , Maksimum değer: f (1) = e .
C2. f ( x ) = 1− x , [−1, 1 ] ⇒ f ′( x) = −
.
.
.
1
⇒ KN yok
2 1− x
.
.
noktalarında EN yok !. Uç noktaları inceleyelim:
4
____________________
http://odev.110mb.com
⇒
N
Not 2 den
Aralığın iç
f ′( x) = −
1
< 0 ⇒ f Azalan ⇒ x = 1 m.minimum, x = −1 m.maksimum ⇒
2 1− x
.
.
.
Minimum değer: f (1) = 0 , Maksimum değer: f (−1) = 2 .
⎧⎪.1− x
, 0 ≤ x <1
C3. f ( x) = ⎪⎨
⇒ Dikkat edilirse fonksiyon x = 2 de sürekli değildir
⎪⎪⎩.2 x − 4. ,2 ≤ x ≤ 3..
dolayısıyla bu noktada türevlenemez. Fonksiyonun grafiği üzerinde inceleme yapıp sonuca
gidelim:
x = 2 EN değil. Aralığın iç noktalarında EN
yok. x = 3 m.maksimum ⇒ Maksimum değer:
f (3) = 2 .
⎧⎪ .x 2
, −1 ≤ x < 0
⎪
C4. f ( x) = ⎨
⇒ Dikkat edilirse fonksiyon x = 0 da sürekli değildir
2
⎪⎪.2 − x ,..0 ≤ x ≤ 1...
⎩
dolayısıyla bu noktada türevlenemez. Fonksiyonun grafiği üzerinde inceleme yapıp sonuca
gidelim:
x = 0 y.maksimum ve m.maksimum. Aralığın
diğer iç noktalarında EN yok. f (−1) = f (1) = 1
⇒ Maksimum değer: f (0) = 2 .
⎧
⎪
⎪⎪ f ′( x) = 3x 2 −12 x + 9 = 3( x −1)( x − 3) = 0
⎪
C5. f ( x ) = x 3 − 6 x 2 + 9 x + 2 , [−1, 4 ] , KN. : ⎪⎨
⇓
⎪⎪
x1 = 1, .x2 = 3
⎪⎪
⎩⎪
.
.
⇒ f ′′( x) = 6 x −12 ⇒ f ′′(1) = −6 < 0
.
.
⇒
N
ikinci türev testinden
f ′′(3) = 6 > 0
.
.
⇒
N
x = 3 y.minimum.
ikinci türev testinden
5
____________________
http://odev.110mb.com
x = 1 y.minimum,
f (−1) = −14 , f (1) = f (4) = 6 , f (3) = 2 ⇒ Minimum değer: f (−1) = −14 , Maksimum
değer: f (1) = f (4) = 6 .
C6. f ( x) =
f (1) =
x
, [0, 2 ] . Cevabı: Minimum değer: f (0) = 0 , Maksimum değer:
x +1
2
.
.
1
.
2
..
Önbilgi 2 ( i ) (konvekslik-konkavlık ) Şekil üzerinde açıklayacağız.
bütün teğetler f in grafiğinin altında
bütün teğetler g nin grafiğinin üzerinde
konveks
konkav
Not 5: (kabaca) Konveks:
, Konkav:
(.ii.) ( f ′′ ile f in grafiği arasındaki ilişki) (Konvekslik Testi)
(.ii.) -T1. “ ∀x ∈ I için f ′′( x) > 0 ” ⇒ f : I da konveks.
.
.
(.ii.) -T2. “ ∀x ∈ I için f ′′( x) < 0 ” ⇒ f : I da konkav.
.
.
6
____________________
http://odev.110mb.com
( iii ) (Büküm noktası) Eğrinin konvekslikten konkavlığa (veya konkavlıktan konveksliğe)
.
.
geçtiği noktaya Büküm (Dönüm-Eğer) noktası denilir. Ör:
x = 0 noktası büküm noktasıdır.
( iii ) (Asimptotlar: fonksiyona sonsuzda teğet olan eğriler ) Daha çok f ( x) =
.
.
p ( x)
q ( x)
şeklindeki rasyonel ifadelerde rastlanılır (p,q: polinom). Sorulara uygunluk açısından kabaca
açıklama:
(Düşey Asimptot: paydayı sıfır yapan değerlerde ) f ( a−) , f ( a+) değerlerinden biri −∞
diğeri +∞ a eşit ⇒ x = a f in bir D.Asimptotudur.
(Yatay Asimptot: x → −∞ , x → +∞ için limitlerde) lim f ( x) = b ∈ \ ⇒ y = b f in bir
x→∞
Y.Asimptotudur.
(Eğri Asimptot: payın derecesi paydanınkinden bir büyük)
m = lim
x→∞
f ( x)
, lim ( f ( x) − mx ) = n ∈ \ ⇒ y = mx + n f in bir E.Asimptotudur.
x→∞
x
Örnekler: f ( x) =
1
fonksiyonu için x = 1 D.Asimptot, y = 0 Y.Asimptottur.
x −1
x3 + 1
f ( x) = 2
fonksiyonu için y = x + 2 E.Asimptottur.
x − 2x
(.II.) Fonksiyon grafiklerinin çizimi ile ilgili sorularda, aşağıdaki aşamaları takip edeceğiz:
A. Fonksiyonun tanım kümesinin ve eksenleri kestiği noktaların belirlenmesi.
B. Asimptotların belirlenmesi.
C. Birinci ve İkinci türevlerin, EN.ların, Konveks-Konkav olduğu bölgelerin belirlenmesi.
7
____________________
http://odev.110mb.com
1.
f ( x) = x 4 − 8 x 2
y = x 4 − 8 x 2 = x 2 ( x 2 − 8)
A.
x = 0 için y = 0
y = 0 için x = − 8, x = 8
.
.
⎫
⎪
⎪ ⇒ (0, 0) , −
(
⎬
⎪
⎪
⎭
) (
8, 0 ,
.
.
.
)
8, 0 ; T.K: \
.
.
.
B. Asimptot yok!
C. f ′( x) = 4 x 3 −16 x = 4 x ( x − 2)( x + 2) ,
2
2
f ′′( x) = 12 x 2 −16 = 4(3x 2 − 4) = 12( x −
).( x +
)
3
3
.
x
0
−2
−∞
f ′( x )
.
2
+
−
∞
+
−
∞
f ( x)
∞
−16
0
y .m in im u m
y .m a k s im u m
2
3
−
x
−16
y .m in im u m
2
3
f ′′( x)
+
−
+
Konvekslik
konveks
konkav
konveks
−
80
9
büküm n.
8
____________________
http://odev.110mb.com
−
80
9
büküm n.
Çizime Hazırlık
2.
f ( x ) = x 4 − 6 x 2 benzer şekilde:
9
____________________
http://odev.110mb.com
3.
f ( x) =
A.
x2
x2 + 3
⎫
⎪
⎪ ⇒ (0, 0) ; T.K: \
⎬
⎪
⎪
⎭
x2
x2 + 3
x = 0 için y = 0
y=
x2
= 1 ⇒ y = 1 Y.Asimptot
B. lim f ( x) = lim 2
x→∞
x→∞ x + 3
C. f ′( x) =
6x
2
( x 2 + 3)
, f ′′( x) = −
18( x +1)( x −1)
3
( x2 + 3)
x
0
−∞
f ′( x )
∞
+
−
∞
f ( x)
∞
0
y .m in im u m
x
−1
1
f ′′( x)
−
+
−
Konvekslik
konkav
konveks
konkav
1
4
4
büküm n.
büküm n.
10
____________________
http://odev.110mb.com
1
4.
f ( x ) = x 2 − x + 12 benzer şekilde:
5.
f ( x) = x −
A.
1
x
x 2 −1
x2
x = 0 için x = −1, x = 1
y=
1
f (0−) = lim x − = ∞
. x.→.0−
x
1
f (0+) = lim x − = −∞
. x.→.0+
x
B.
m = lim
x→∞
f ( x)
x 2 −1
= lim
= 1,
x→∞ x 2
x
⎛
⎞
1
lim ( f ( x) − mx) = lim ⎜⎜ x − − x⎟⎟⎟
⎜
⎠
x→∞
x→∞ ⎝
x
1
= lim − = 0 (= n)
x→∞ x
⎫
⎪
⎪ ⇒ (−1, 0 ) , ( 1, 0 ) ; T.K: \ \ {0}
⎬
⎪
⎪
⎭
⎫
⎪
⎪ ⇒ x = 0 D.Asimptot
⎬
⎪
⎪
⎭
⎫
⎪
⎪
⎪
⎪ ⇒ y = mx + n yani y = x E.Asimptot
⎬
⎪
⎪
⎪
⎪
⎭
.
1
2
, f ′′( x) = − 3
2
x
x
EN yok !
⇒
N
C. f ′( x) = 1 +
KN yok
Not 2 den
11
____________________
http://odev.110mb.com
.
.
.
.
x
−∞
f ′( x )
∞
+
+
+
−∞
f ( x)
∞
x
0
f ′′( x)
+
−
Konvekslik
konveks
konkav
büküm n.
6.
A.
f ( x) =
x
x −1
x
x −1
x = 0 için y = 0
y=
x
= −∞
. x.→.1− x −1
1
f (1+) = lim x − = ∞
. x.→.1+
x
f (1−) = lim
B.
⎫
⎪
⎪ ⇒ (−1, 0 ) , ( 1, 0 ) ; T.K: \ \ {1}
⎬
⎪
⎪
⎭
⎫
⎪
⎪ ⇒ x = 1 D.Asimptot
⎬
⎪
⎪
⎭
.
12
____________________
http://odev.110mb.com
.
.
.
.
x2
lim f ( x) = lim 2
= 1 ⇒ y = 1 Y.Asimptot
x→∞
x→∞ x + 3
C. f ′( x) = −
1
2
( x −1)
, f ′′( x) =
x
2
3
( x −1)
f ( x)
EN yok !
Not 2 den
1
−∞
f ′( x )
⇒
N
, KN yok
∞
−
1
−
−∞
x
1
∞
1
f ′′( x)
−
+
Konvekslik
konkav
konveks
büküm n.
13
____________________
http://odev.110mb.com
7.
x2
f ( x) = 2
benzer şekilde ( x = −1, x = 1 D.Asimptot; y = 1 Y.Asimptot; x = 0
x −1
y.maksimum):
14
____________________
http://odev.110mb.com