Serbest Cisim Diyagramı

Seventh Edition
VECTOR MECHANICS FOR
ENGINEERS: STATICS
Ferdinand P. Beer
E. Russell Johnston, Jr.
Ders Notu:
Hayri ACAR
İstanbul Teknik Üniveristesi
4. Rijit
Cisimlerin
Dengesi
Tel: 285 31 46 / 116
E-mail: [email protected]
Web: http://atlas.cc.itu.edu.tr/~acarh
© 2002 The McGraw-Hill Companies, Inc. All rights reserved.
• Rijit cisimler statik olarak dengede ise, dış kuvvetler ve momentler
dengededir ve cisime herhangi bir öteleme ve dönme hareketi vermezler.
• Statik denge halindeki cisimler için gerekli olan denklem:
r
r
r r
∑ F = 0 ∑ M O = ∑ (r × F ) = 0
• Her kuvvet ve moment dik bileşenlerine ayrılırsa 6 skaler denklem oluşur:
∑ Fx = 0 ∑ Fy = 0 ∑ Fz = 0
∑Mx = 0 ∑My = 0 ∑Mz = 0
Serbest Cisim Diyagramı
Statik denge analizinde ilk işlem cisime etki eden
tüm kuvvetlerin Serbest Cisim Diyagramı ile
belirlenmesidir.
• İncelenecek eleman seçilir ve tüm elemanlardan
izole edilir.
• Cisimin ağırlığı da dahil olmak üzere tüm dış
kuvvetlerin şiddeti, yönü ve uygulama noktası
belirlenir.
• Bilinmeyen kuvvetlerin uygulama noktası
belirlenir yönü tahmin edilir. Bu kuvvetler
genelde, cisimin hareketini engeleyen, bağlantı
noktalarından gelen tepki kuvvetleridir.
• Kuvvetlerin
momentini
hesaplarken
kullanılacak gerekli boyutlandırma yapılır.
İki Boyutlu Yapılarda Bağlantı ve Destek
Noktalarındaki Tepki Kuvvetleri
• Bilinen doğrultudaki tepki
kuvvetleri
Kayıcı mafsal
Kısa kablo
Sürtünmesiz
çubukta
yüzük
Sürtünmesiz
yüzey
Pandül ayak
Yarıkta
sürtünmesiz pim
Tesir çizgisi bilinen
tek kuvvet
Tesir çizgisi bilinen
tek kuvvet
Tesir çizgisi bilinen
tek kuvvet
veya
Mafsal
Pürüzlü yüzey
Bilinmeyen doğrultudaki
tepki kuvveti
veya
Ankastre mesnet
• Bilinmeyen doğrultudaki
tepki kuvvetleri
• Bilinmeyen doğrultudaki
tepki kuvvetleri ve
momenti
Bilinmeyen doğrultudaki tepki
kuvveti ve momenti
Mafsal
R2
R1
Kayıcı mafsal
R1
Ankastre mesnet
M
R2
R1
STATİK YÜKLER
DİNAMİK YÜKLER
İki Boyutlu Halde Rijit Cisim Dengesi
• İki boyutlu yapıya etkiyen tüm kuvvetler ve
momentler için:
Fz = 0 M x = M y = 0 M z = M O
• Denge denklemi:
∑ Fx = 0 ∑ Fy = 0 ∑ M A = 0
A noktası yapının düzlemindeki her hangi
bir noktadır.
• Bu denklemler 3 bilinmeyen için
kullanılabilir.
• Bu 3 denkleme ilave yapılamaz ama
denklemler değiştirilebilir.
∑ Fx = 0 ∑ M A = 0 ∑ M B = 0
Statikçe Belirsizlik
• Denklem sayısından
fazla bilinmeyen
varsa.
• Denklem sayısından
az bilinmeyen varsa.
• Denklem sayısıyla eşit
bilinmeyen var fakat
yetersiz bağlantı varsa.
Örnek Problem 4.1
Çözüm:
• Vincin Serbest Cisim Diyagramını çizilir.
• A noktasına göre moment denge
denklemi kullanılarak B bağlantı
noktasındaki tepki hesaplanır.
Sabit bir vinç 1000 kg kütleye
sahiptir ve 2400 kg kütleli sandığı
kaldırmakta kullanılmaktadır. Vinç
duvara A noktasından mafsal ile ve
B noktasından kayıcı mafsal ile
sabitlenmiştir.
Vincin
ağırlık
merkezi G noktasıdır.
A ve B noktasındaki
kuvvetlerini bulunuz.
tepki
• Yatay ve düşey kuvvet dengesi
denklemleri kullanılarak A bağlantı
noktasındaki kuvvetler hesaplanır.
• B noktasına göre moment denge
denklemi
kullanılarak
yukarıda
bulunan sonuçların sağlaması yapılır.
• A noktasına göre moment denge
denklemi kullanılarak B bağlantı
noktasındaki tepki hesaplanır.
∑ M A = 0 : + B(1.5m ) − 9.81 kN(2m )
− 23.5 kN(6m ) = 0
B = +107.1 kN
• Yatay ve düşey kuvvet dengesi
denklemleri kullanılarak A bağlantı
noktasındaki kuvvetler <hesaplanır.
∑ Fx = 0 : Ax + B = 0
Ax = −107.1 kN
∑ Fy = 0 : Ay − 9.81 kN − 23.5 kN = 0
• Serbest Cisim Diyagramı
Ay = +33.3 kN
Örnek Problem 4.3
24 cm
Bir yükleme vagonu ray üzerinde, bir
halat yardımı ile, dengededir. Vagonun
ağırlığı yüküyle birlikte 5500 N dur ve G
noktasına uygulanmaktadır.
25 cm
25 cm
Halattaki kuvveti ve her tekerlekteki tepki
kuvvetini bulunuz.
cm
30
• SCD
• Tekerleklerdeki tepki kuvvetleri:
∑M
A
= 0 : − (2320 N ) 25cm. − (4980 N )6cm
+ R2 (50cm ) = 0
R2 = 1758 N
6 cm
2320 N
25cm
cm
25
4980 N
25 cm
25 cm
∑M
= 0 : + (2320N) 25cm− (4980N)6cm
B
− R1(50cm) = 0
R1 = 562N
Wx = +(5500 N )cos 25o
= +4980 N
Wy = −(5500 N )sin 25
o
= −2320 N
• Halattaki kuvvet:
∑F
x
= 0 : + 4980 N − T = 0
T = +4980 N
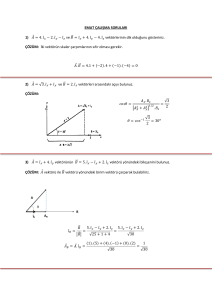
Örnek Problem 4.4
Şekildeki yükleme elemanındaki kablodaki
kuvvet 150 kN dur.
E noktasındaki tepki kuvvetini bulunuz.
• 3 denge denklemi kullanılarak tepki
kuvvetleri bulunabilir.
4. 5
(150 kN ) = 0
∑ Fx = 0 : E x +
7.5
E x = −90.0 kN
SCD
62 + 4.52 = 7.5m
∑ Fy = 0 : E y − 4(20 kN ) −
6
(150 kN ) = 0
7.5
E y = +200 kN
∑ M E = 0 : + 20 kN(7.2 m ) + 20 kN(5.4 m )
+ 20 kN(3.6 m ) + 20 kN(1.8 m )
−
6
(150 kN )4.5 m + M E = 0
7.5
M E = 180.0 kN ⋅ m
İki Kuvvet Etkisi Altında Statik Denge
• F1 ve F2 gibi iki kuvvet etkisi altında bir plaka
düşünelim.
• Statik denge için, A noktasına göre toplam
momentin sıfır olması gerekir. F2 kuvvetinin
momenti sıfır olmalıdır. Bunun için F2 kuvvetinin
tesir çizgisi A noktasından geçmelidir.
• Benzer olarak F1 kuvvetinin tesir çizgisi B
noktasından geçmelidir.
• Kuvvet denge denklemi kullanılırsa, F1 ve F2 nin
eşit şiddetli ve zıt yönlü olması gerektiği bulunur.
Üç Kuvvet Etkisi Altında Statik Denge
• Rijit cisime 3 kuvvet etki ettiğini düşünelim
• İki kuvvetin, F1 ve F2 , kesiştiği nokta D olsun.
• Rijit cisim denge denklemi nedeniyle D noktasına
göre toplam momentin sıfır olması gerekir. Bunun
için F3 kuvvetinin tesir çizgisinin D noktasından
geçmesi gerekir.
Örnek Problem 4.6
Bir adam 10 kg’lık 4 m uzunluğundaki kirişi bir halat ile
kaldırmaktadır.
Halattaki kuvveti ve A noktasındaki tepki kuvvetini bulunuz.
SCD
CE
tan α =
AE
• A noktasındaki tepki kuvveti R nin yönü:
AF = AB cos 45 = (4 m )cos 45 = 2.828 m = BF
CD = AE = 12 AF = 1.414 m
BD = CD tan(90 − (45 + 20)) = (1.414 m ) tan 20 = 0.515 m
CE = BF − BD = (2.828 − 0.515) m = 2.313 m
CE 2.313
o
tanα =
=
= 1.636
α
=
58
.
6
AE 1.414
• A noktasındaki tepki kuvveti R nin şiddeti:
T
sin 31.4
o
=
R
sin 110
T = 81.9 N
R = 147.8 N
o
=
98.1 N
sin 38.6o
Üç Boyutlu Halde Rijit Cisim Dengesi
• Üç boyutlu halde 6 skaler denge denklemi:
∑ Fx = 0 ∑ Fy = 0 ∑ Fz = 0
∑Mx = 0 ∑My = 0 ∑Mz = 0
• Bu denklemler 6 bilinmeyen kuvvet ve moment için kullanılabilir.
• Vektörel haldeki denge denklemleri:
r
r
r r
∑ F = 0 ∑ M O = ∑ (r × F ) = 0
Üç Boyutlu Yapılarda Bağlantı ve Destek
Noktalarındaki Tepki Kuvvetleri
Bilya
Pürüzsüz yüzey
Pürüzlü yüzey üzerinde
makara
Tesir çizgisi bilinen
tek kuvvet
Kablo
Tesir çizgisi bilinen
tek kuvvet
İki kuvvet bileşeni
Ray üzerinde makara
Üç kuvvet bileşeni
Pürüzlü yüzey
Küresel mafsal
Üniversal
mafsal
Üç kuvvet bileşeni ve
bir kuvvet çifti
Ankaster mesnet
Yalnız radyal yükleri aktarabilen mafsal ve yatak
Pim ve konsol
Eksenel ve radyal yükleri
aktarabilen mafsal ve yatak
Üç kuvvet bileşeni ve
üç kuvvet çifti
İki kuvvet bileşeni
(ve iki kuvvet çifti)
Üç kuvvet bileşeni
(ve iki kuvvet çifti)
Örnek Problem 4.8
2m
8m
4m
3m
6m
2m
5m
Üniform yoğunluğa sahip plaka 270 N ağırlığındadır ve A noktasından küresel
mafsal ile duvara bağlanmıştır. Ayrıca duvara C ve D noktasından bağlanmış
halatlarla desteklenmektedir.
Her kablodaki kuvvetleri bulunuz.
SCD
2m
8m
4m
3m
6m
2m
W = -(270N)j
4m
4m
• A noktasındaki bağlantı şekli
nedeniyle 3 bilinmeyenli tepki
kuvveti vardır. Plaka x ekseni
etrafında döenbilmektedir.
r
r
r
rD − rB
TBD = TBD r
r
rD − rB
r
r
r
− 8i + 4 j − 8k
= TBD
12
r 1r 2r
2
= TBD − 3 i + 3 j − 3 k
r r
r
rC − rE
TEC = TEC r r
rC − rE
r
r
r
− 6i + 3 j + 2 k
= TEC
7
r 3r 2r
6
= TEC − 7 i + 7 j + 7 k
(
)
(
)
2m
8m
4m
3m
6m
2m
r r r
r
r
∑rF = A + TBD + TEC − (270 N ) j = 0
i : Ax − 23 TBD − 76 TEC = 0
r
j : Ay + 13 TBD + 73 TEC − 270 N = 0
r
k : Az − 23 TBD + 72 TEC = 0
r
r r
r r
∑ M A r= rB × TBD + rEr× TEC
+ (4 m )i × (− 270 N ) j = 0
r
j : 5.333TBD − 1.714 TEC = 0
r
k : 2.667 TBD + 2.571TEC − 1080 N = 0
W = -(270N)j
4m
4m
5 denklem 5 bilinmeyen var:
TBD = 101.3 lb TEC = 315 lb
r
r
r
v
A = (338 lb )i + (101.2 lb ) j − (22.5 lb )k
Örnek Problem
menteşe
5 kN
H
45o
B
A
G
8m
7m
15m
6m
Şekildeki yükleme elemanındaki mesnet tepkilerini hesaplayınız.
Üniform ağırlığa sahip kirişin 1 m’si 147 N ağırlığındadır.
5 kN
45o
H
B
A
G
8m
45o
7m
5 kN
15 m
6m
147x30=4410 N
HH
SCD
VG
VH
147x6=882 N
VH
MA
HH
HA
3m3m
VA
45o
5 kN
15 m
VG
147x30=4410 N
15 m
147x6=882 N
HH
VH
MA
VH
HA
HH
+
+
+
Σ FX
HH
Σ FY
3m3m
= 0 = (5 kN cos 45 ) - HH
= 3.54 kN
= 0 = VH + VG - (5 kN cos 45)
- 4.41 kN
VH + VG = 7.95 kN
Σ MH
= 0 = +(5 kN cos 45) * 22 m
-(VG * 15 m)
+(4.41kN*15m)
VG = 9.60 kN , VH = -1.65 kN =1.65 kN
VA
45o
5 kN
HH=3.54 kN
4.41 kN
1.65 kN
882 N
MA
VG=9.6 kN
VH=1.65 kN
HA
3.54 kN
3m3m
+ ΣF
X
+
Σ FY
+ Σ MA
=0
HA
= 3.54 - HA
= 3.54 kN
=0
VA
= 1.65 kN + VA - 0.882
= - 0.768 kN = 0.768 kN
=0
MA
= -(1.65 kN * 6 m) + (0.882 * 3m) + MA
= 7.25 kNm = 7.25 kNm
VA
45o
5 kN
4.41 kN
HH=3.54 kN
VG=9.6 kN
VH=1.65 kN
VH = 1.65 kN
MA = 7.25 kNm
HA = 3.54 kN
HH = 3.54 kN
0.882 kN
VA = .768 kN
Örnek Problem
φ
m
L
menteşe
M
• M kütleli lamba m kütleli ve L uzunluğunda kirişin ucuna
asılmıştır. Kiriş duvara menteşe ile bağlanmıştır ve diğer
ucundan ağırlıksız kablo ile desteklenmektedir.
– Kablodaki kuvveti bulunuz.
– Mesnet tepkisini bulunuz.
SCD
T
φ
M
B
L/2
y
Fy
m
A
+
Fx
∑M
B
= 0:
L
LMg+ mg - LTsinφ = 0
2
x
(
M + m )g
2
T =
L/2
mg
Mg
sin φ
∑F =0
x:
T cos φ + Fx = 0
y:
T sin φ + Fy - Mg - mg = 0
Fx =
(
− M +m
tan φ
2
1
Fy = mg
2
)g
Örnek Problem
φ
Can
L
m
F
d
• Can (kütlesi: M) duvara φ açısı ile dayanmış olan
merdivene tırmanmaktadır (uzunluğu: L, kütlesi: m).
Duvarlar sürtünmesiz yüzeye sahip ise Can’ın düşmesini
engellemek için gerekli olan F kuvvetini bulunuz.
B
SCD
L/2
φ
NB
x:
F =0
y:
∑
y
-NB+ F = 0
NA - Mg – mg = 0
x
mg
d
F
Mg
A
NA
+
∑M
B
=0
L
sin φ mg + (L − d )sin φ ⋅ Mg + Lcos φ F - Lsin φ ⋅ N A = 0
2
m 
d
F = Mg tanφ  +

 L 2M 
Hangisi statik olarak belirlidir?
statikçe belirli
statikçe belirli
fazla bağlantı
statikçe belirsiz
x yönünde
belirsiz
A
yetersiz
bağlantı
A noktası etrafında dönme meydana gelir