FIZ 312 - Giresun Üniversitesi Fizik

KUANTUM MEKANİĞİ – II DERSİ BİLGİ FORMU
Dersin Adı
Dersin Kodu
Dersin Türü
Dersin Seviyesi
Dersin AKTS Kredisi
Haftalık Ders Saati (Kuramsal)
Haftalık Uygulama Saati
Haftalık Laboratuar Saati
Dersin Verildiği Yıl
Dersin Verildiği Yarıyıl
Dersin Öğretim Üyesi (Üyeleri)
Öğretim Sistemi
Eğitim Dili
Dersin Ön Koşulu Olan Ders
Ders İçin Önerilen Diğer
Hususlar
Staj Durumu
Dersin Amacı
Dersin İçeriği
Haftalık Ayrıntılı
Ders İçeriği
Kuantum Mekaniği – II
FIZ 312
Zorunlu
Lisans
5
4
0
0
3
6
Doç. Dr. Birol ERTUĞRAL
Yüz yüze
Türkçe
Yok
Yok
Yok
Bu dersin amacı, kuantum mekaniğindeki temel kavramları
ve bu kavramların uygulamalarını öğretmektir.
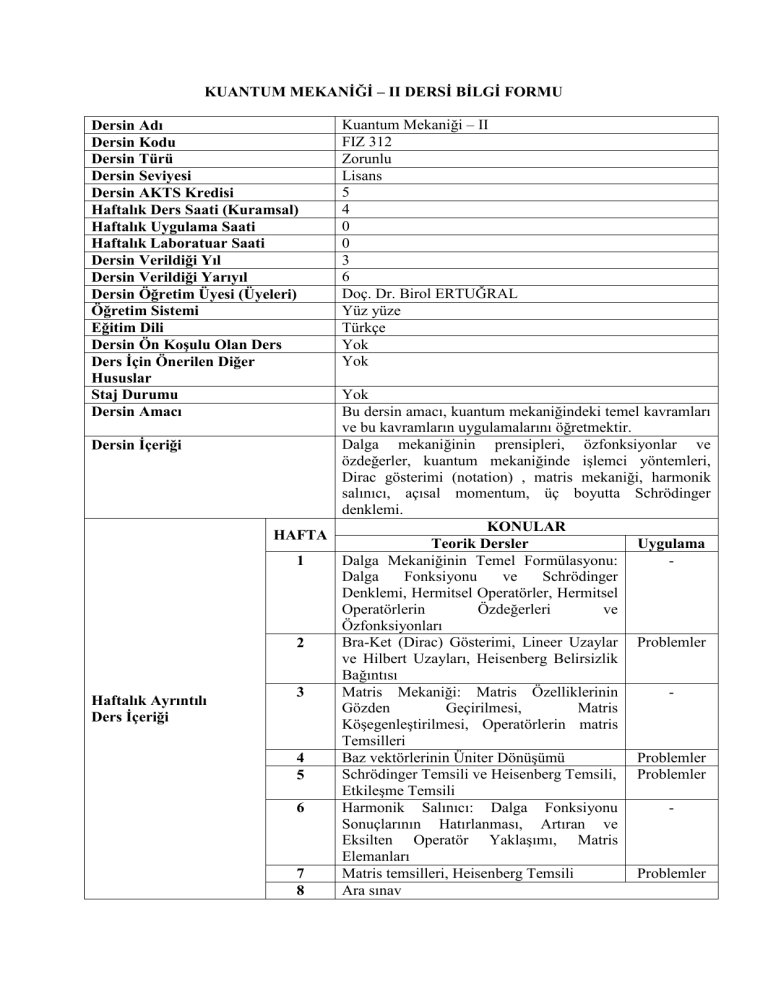
Dalga mekaniğinin prensipleri, özfonksiyonlar ve
özdeğerler, kuantum mekaniğinde işlemci yöntemleri,
Dirac gösterimi (notation) , matris mekaniği, harmonik
salınıcı, açısal momentum, üç boyutta Schrödinger
denklemi.
KONULAR
HAFTA
Teorik Dersler
Uygulama
Dalga Mekaniğinin Temel Formülasyonu:
1
Dalga
Fonksiyonu
ve
Schrödinger
Denklemi, Hermitsel Operatörler, Hermitsel
Operatörlerin
Özdeğerleri
ve
Özfonksiyonları
Bra-Ket (Dirac) Gösterimi, Lineer Uzaylar Problemler
2
ve Hilbert Uzayları, Heisenberg Belirsizlik
Bağıntısı
Matris Mekaniği: Matris Özelliklerinin
3
Gözden
Geçirilmesi,
Matris
Köşegenleştirilmesi, Operatörlerin matris
Temsilleri
Baz vektörlerinin Üniter Dönüşümü
Problemler
4
Schrödinger
Temsili
ve
Heisenberg
Temsili,
Problemler
5
Etkileşme Temsili
Harmonik Salınıcı: Dalga Fonksiyonu
6
Sonuçlarının Hatırlanması, Artıran ve
Eksilten Operatör Yaklaşımı, Matris
Elemanları
Matris temsilleri, Heisenberg Temsili
Problemler
7
Ara sınav
8
Açısal Momentum Teorisi: yörünge Açısal
Momentumu ve Sıradeğişim Bağıntıları
Küresel Harmonikler, Genel Operatör
10
Yöntemleri
Açısal Momentum Operatörlerinin Matris
11
Temsilleri
Açısal Momentumların Toplanması
Problemler
12
Küresel Koordinatlarda Schrödinger
13
Denklemi, Değişkenlere Ayırma
Hidrojen Atomu
Problemler
14
Genel tekrar ve Problem Çözümü
15
Dönem sonu sınavı
16
ÖÇ - 1: Dalga mekaniğinin temel formülasyonundaki temel
kavramları açıklayabilecektir.
ÖÇ - 2: Hermitsel operatörün özdeğerlerinin gerçel (reel) olması
gerektiğini tartışabilecektir.
ÖÇ - 3: Sıra değişimli iki operatörün, aynı anda özfonksiyonu
olabilen fonksiyonların bulunabileceğini açıklayabilecektir.
ÖÇ - 4: Dirac tarafından ortaya konan Bra-Ket notasyonunu
tanımlayabilecektir.
ÖÇ - 5: Matris mekaniğindeki temel kavramları açıklayabilecektir.
ÖÇ - 6: Shrödinger ve Heisenberg Temsilini açıklayabilecek ve
harmonik salınıcı problemine uygulayabilecektir.
ÖÇ - 7: Harmonik salınıcı probleminde eksilten a ve artıran a+
operatörlerini tanımlayabilecek ve bunlarla ilgili operatörlerin
( a, aa, aa+ , a+a+ , a+a) matris temsilini bulabilecektir.
ÖÇ - 8: Yörünge açısal momentumunu açıklayabilecek ve konum,
lineer momentum ve açısal momentum arasındaki sıra
değişim bağıntılarını yazabilecektir.
ÖÇ - 9: Küresel harmonikleri açıklayabilecek ve L2 ve Lz
operatörleri için özdeğer denklemlerini yazabilecektir.
ÖÇ-10: Genel açısal momentum operatörü yaklaşımını
tanımlayabilecektir.
DERS KİTABI:
Gasiorowicz, Stephen.2003, Quantum Physics, John Wiley and Sons
Inc.
9
Öğrenme Çıktıları
Ders Kitabı/
Malzemesi/
Önerilen
Kaynaklar
DERS ARAÇLARI:
DEĞERLENDİRME
Yarıyıl (Yıl) İçi Etkinlikleri
Sayısı
Ara sınav
1
TOPLAM
1
Yarıyıl (Yıl) İçi Etkinliklerinin Başarı
Notuna Katkısı
Yarıyıl (Yıl) Sonu Sınavının Başarı
Notuna Katkısı
TOPLAM
Yarıyıl (Yıl) Notuna Katkısı %
100
100
40
60
100
Dersin Öğrenme, Öğretme ve Değerlendirme Etkinlikleri Çerçevesinde
İş Yükünün Hesaplanması
Etkinlikler
Sayısı
Süresi
Toplam İş Yükü
(Saat)
(Saat)
Yüz yüze Eğitim
14
4
56
Sınıf dışı çalışma
14
4
56
5
Ara sınav için hazırlık
3
15
Ara sınav
1
2
2
Dönem sonu sınavı için
4
5
20
hazırlık
Dönem sonu sınavı
1
2
2
TOPLAM İŞ YÜKÜ (Saat) = 151
DERSİN AKTS KREDİSİ= Toplam İş Yükü(saat)/(30saat/AKTS)=5
Program ve Öğrenme Çıktıları İlişkisi
Ders
Öğrenme
Çıktıları
Program Çıktıları
PÇ PÇ PÇ PÇ PÇ PÇ PÇ PÇ PÇ PÇ PÇ PÇ
1
2
3
4
5
6
7
8
9 10 11 12
ÖÇ 1
ÖÇ 2
ÖÇ 3
ÖÇ 4
ÖÇ 5
ÖÇ 6
ÖÇ 7
ÖÇ 8
ÖÇ 9
ÖÇ 10
ÖÇ 11
ÖÇ 12
*Katkı Düzeyi: 1 Çok düşük
2 Düşük
3 Orta
4 Yüksek
5 Çok yüksek
QUANTUM MECHANICS – II INDIVIDUAL COURSE DESCRIPTION
Quantum Mechanics - II
FIZ 312
Compulsory
Undergraduate
5
Course Unit Title
Course Unit Code
Type of Course Unit
Level of Course Unit
Number of ECTS Credits
Allocated
Theoretical (hour/week)
Practice (hour/week)
Laboratory (hour/week)
Year of Study
Semester when the course
unit is delivered
Name of Lecturer (s)
Mode of Delivery
Language of Instruction
Prerequisities and corequisities
Recommended Optional
Programme Components
Work Placement(s)
Objectives of the Course
4
0
0
3
6
Assoc. Prof. Dr. Birol ERTUĞRAL
Face to face
Turkish
None
None
Course Contents
WEEKS
1
2
Weekly Detailed
Course Contents
3
4
5
6
None
The objective of this course is to teach the fundamental
concepts and the application of these concepts in quantum
mechanics.
Principles of wave mechanics, eigenfunctions and
eigenvalues, operator methods in quantum mechanics,
Dirac notation, matrix mechanics, harmonic oscillator,
angular momentum, Schrödinger equation in three
dimensions.
TOPICS
Theoretical Courses
Application
Basic Formulation of Wave Mechanics: The
Wave Function and Schrödinger Equation,
Hermitian Operators, Eigenvalues and
Eigenfunctions of Hermitian Operators
Bra-Ket Notation, Linear Vector Spaces and
Problems
Hilbert Spaces, Heisenberg Uncertainty
Relation
Matrix Mechanics: Review of Matrix
properties,
Matrix
Diagonalization,
Representations of Operators by Matrices
Unitary Transformation of The Basis States
Problems
The Schrödinger Picture and Heisenberg
Problems
Picture, Interaction Picture
Harmonic Oscillator: Review of the Wave
Function Results, Raising and Lowering
7
8
9
10
11
12
13
14
15
16
Operator Aproach, Matrix Elements
Matrix Represantations, Heisenberg Picture
Mid-term exam
Angular Momentum Theory: Orbital
Angular Momentum and Commutation
Relations
Spherical Harmonics, General Operator
Methods
Matrix Representations of Angular
Momentum Operators
Addition Of Angular Momenta
Schrodinger Equation in Spherical
Coordinates, Seperation of Variables
The Hydrogen Atom
General Review and Problem Solutions
End-of-term exam
Problems
-
Problems
Problems
-
Learning Outcomes
LO - 1: Explain the fundemental concepts in basic formulation of wave
mechanics
LO - 2: Discuss the fact that the eigenvalues of a Hermitian operators
should be real.
LO - 3: Explain that there exists functions which are simultaneously
eigenfunction of two commutative operators.
LO - 4: Define the Bra-Ket notation introduced by Dirac.
LO - 5: Explain the fundemental concepts in matrix mechanics.
LO - 6: Explain the Shrödinger and Heisenberg representation and
apply them to harmonic oscillator problems.
LO - 7: Define the lowering a and raising operator a+ in harmonic
oscillator problem and find the matrix represetation of various
operators such as a, aa, aa+ , a+a+ , a+a.
LO - 8: Explain the orbital angular moentum and write down the
commutation relations between position, momentum operators
and angular momentum operators.
LO - 9: Explain the spherical harmonics and write down the eigenvalue
equations for L2 and Lz operator.
LO - 10: Describe the general angular momentum operator approach.
Textbook/ Material/
Recommended
Readings
Course Book:
Gasiorowicz, Stephen.2003, Quantum Physics, John Wiley and Sons
Inc.
Course Materials:
ASSESSMENT
Semester (Year) Interior
Number
Activities
Laboratory test reports
Laboratory practical exam
Homework
Supervision
1
TOTAL
1
Semester (year) Grades of Domestic
Contribution Activities
Semester (year) of the Final Exam grade
Contribution
TOTAL
Semester (year) Note the %
Contribution to
100
100
40
60
100
Course Learning, Teaching and Assessment Activities in the
Framework Calculation of the workload
Duration
Total workload
Activities
Number
(hour)
(hour)
Fface to face teaching
14
4
56
Own (personal) studies
14
4
56
outside class
Own study for first mid-term
3
5
15
exam
Mid-term exam
1
2
2
Own study for end-of-term
4
5
20
exam
End-of-term exam
1
2
2
TOTAL WORKLOAD (hour) = 151
AKTS CREDIT COURSE= Total Work Load(hour)/(30 hours/AKTS)=5
Contribution of Learning Outcomes to Programme Outcomes
Learning
Outcomes
Programme Outcomes
PO PO PO PO PO PO PO PO PO PO PO PO
1
2
3
4
5
6
7
8
9
10 11 12
LO 1
LO 2
LO 3
LO 4
LO 5
LO 6
LO 7
LO 8
LO 9
LO 10
LO 11
LO 12
*Contribution Level: 1 Very Low
2 Low
3 Medium
4 High
5 Very High