MOMENT

MOMENT
Bir noktaya veya eksene göre bir kuvvetin momenti, kuvvetin cismi o nokta etrafında
döndürmeye çalışmasının bir ölçütüdür. Bu eksen kuvvetin etkime doğrultusu ile
kesişmeyen veya bu doğrultuya paralel olmayan herhangi bir doğru olabilir. Moment
“tork” olarak da adlandırılır.
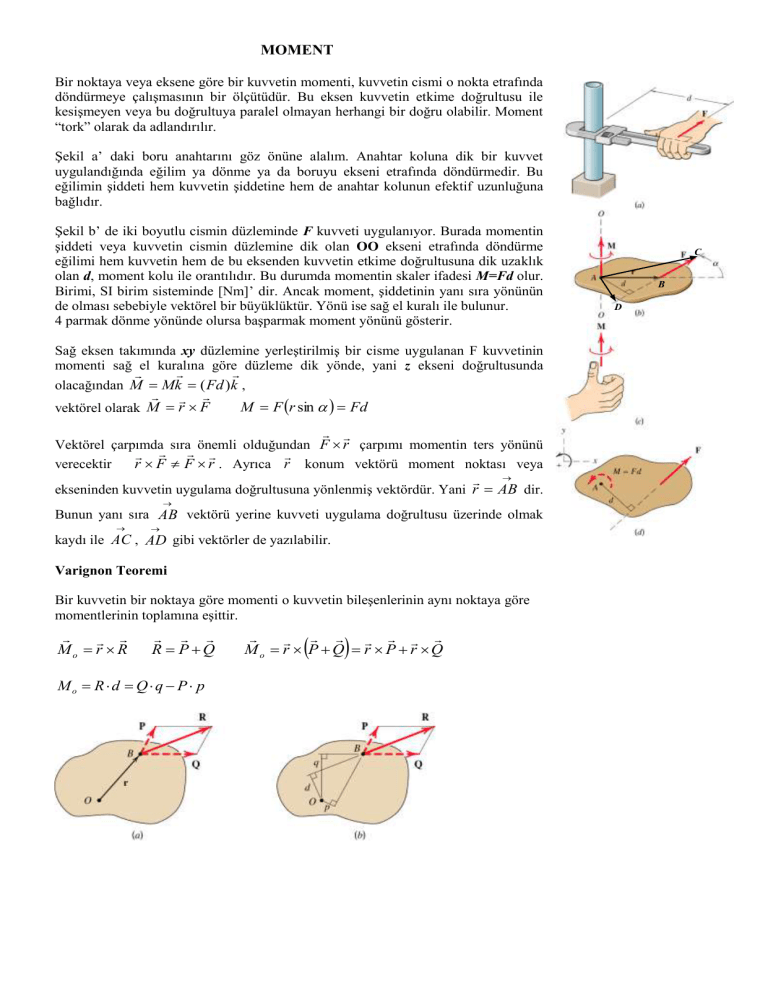
Şekil a’ daki boru anahtarını göz önüne alalım. Anahtar koluna dik bir kuvvet
uygulandığında eğilim ya dönme ya da boruyu ekseni etrafında döndürmedir. Bu
eğilimin şiddeti hem kuvvetin şiddetine hem de anahtar kolunun efektif uzunluğuna
bağlıdır.
Şekil b’ de iki boyutlu cismin düzleminde F kuvveti uygulanıyor. Burada momentin
şiddeti veya kuvvetin cismin düzlemine dik olan OO ekseni etrafında döndürme
eğilimi hem kuvvetin hem de bu eksenden kuvvetin etkime doğrultusuna dik uzaklık
olan d, moment kolu ile orantılıdır. Bu durumda momentin skaler ifadesi M=Fd olur.
Birimi, SI birim sisteminde [Nm]’ dir. Ancak moment, şiddetinin yanı sıra yönünün
de olması sebebiyle vektörel bir büyüklüktür. Yönü ise sağ el kuralı ile bulunur.
4 parmak dönme yönünde olursa başparmak moment yönünü gösterir.
Sağ eksen takımında xy düzlemine yerleştirilmiş bir cisme uygulanan F kuvvetinin
momenti sağ el kuralına göre düzleme dik yönde, yani z ekseni doğrultusunda



olacağından M  Mk  ( Fd )k ,



vektörel olarak M  r  F
M  F r sin    Fd
 
Vektörel çarpımda sıra önemli olduğundan F  r çarpımı momentin ters yönünü
   

r  F  F  r . Ayrıca r konum vektörü moment noktası veya
verecektir


ekseninden kuvvetin uygulama doğrultusuna yönlenmiş vektördür. Yani r  AB dir.

Bunun yanı sıra AB vektörü yerine kuvveti uygulama doğrultusu üzerinde olmak


kaydı ile AC , AD gibi vektörler de yazılabilir.
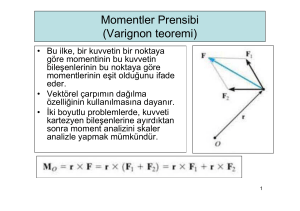
Varignon Teoremi
Bir kuvvetin bir noktaya göre momenti o kuvvetin bileşenlerinin aynı noktaya göre
momentlerinin toplamına eşittir.

 
Mo  r  R
  
R  PQ
Mo  R  d  Q  q  P  p



      
Mo  r  P  Q  r  P  r Q
C
B
D
MOMENT VE KUPL (3 BOYUTLU)
MOMENT

 
Mo  r  F

 
 Mo  F r


i
j

M o  rx ry
Fx
Fy

k
rz
Fz
Eksene göre moment:
Keyfi bir  eksenine göre moment: Öncelikle  ekseni üzerindeki
herhangi bir noktaya göre (örneğin O noktası) moment alınıp elde edilen
moment ile  ekseninin birim vektörü skaler çarpılır. Bu çarpım sonucu
skalerdir. Bir eksene göre momentin vektörel ifadesi gerekiyorsa, eksenin
birim vektörü ile eksene göre momentin skaler değeri (O noktasına göre
momentin eksen üzerindeki izdüşümü) tekrar çarpılır.
    

M    r
 F e  e
 M   
o
(Triple scalar product)
skaler
3 Boyutta Varignon Teoremi


   
    
r  F1  r  F2  ...  r  Fn  r  F1  F2  ...  Fn
