Nokta (Skaler) Çarpım

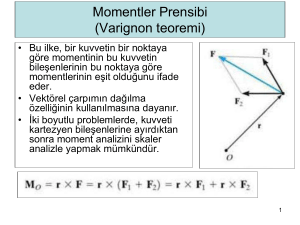
Nokta (Skaler) Çarpım
• Statikte bazen iki doğru arasındaki açının, veya bir
kuvvetin bir doğruya paralel ve dik bileşenlerinin
bulunması gerekir. İki boyutlu problemlerde trigonometri
ile çözülebilir, ancak 3 boyutluda çözüm için vektör
yöntemleri uygulanmalıdır.
• Skaler çarpım, iki vektörün çarpımı için özel bir
yöntemdir.
• A ve B vektörlerinin skaler çarpımı, A⋅⋅B şeklinde yazılır
ve A skaler çarpım B diye okunur. A ve B’nin
büyüklükleri ile iki vektör arasındaki açının kosinüsünün
çarpımı olarak tanımlanır.
r r
A ⋅ B = A ⋅ B cos θ
o
0 ≤ θ ≤ 180
o
1
• Bu çarpıma skaler çarpım veya nokta çarpım da
denir. Bu işlemin kuralları :
– Değişme özelliği (komütatiflik )
– Skaler ile çarpım
– Dağılma kuralı (distributiflik)
r r r r
A⋅ B = B ⋅ A
r r
r r r
r
a ( A ⋅ B ) = (aA) ⋅ B = A ⋅ (aB )
r r r
r r
r r
A ⋅ ( B + D) = ( A ⋅ B) + ( A ⋅ D)
2
Kartezyen vektör formülasyonu
r r
Formülünü kullanarak kartezyen
vektörlerin çarpımını bulmak
A ⋅ B = A ⋅ B cos θ birim
için kullanılabilir.
Örneğin: iˆ ⋅ iˆ = (1)(1) cos 0o = 1
ˆj ⋅ ˆj = 1
kˆ ⋅ kˆ = 1
iˆ ⋅ ˆj = (1)(1) cos 90o = 0
iˆ ⋅ kˆ = 0
kˆ ⋅ ˆj = 0
3
Uygulamalar
• Skaler çarpımın mekanikte iki önemli uygulama
alanı vardır:
– 1) İki vektör veya kesişen doğrular arasındaki açı
4
Uygulamalar
• 2) Bir vektörün bir doğruya paralel ve dik bileşenlerinin
bulunması:
Aa: a-a doğrultusundaki A vektörünün bileşeni. A’nın izdüşümü de denir.
a-a’nın doğrultusu ua birim vektörüyle belirlenmişse, Aa vektörünün şiddeti
skaler çarpımla bulunabilir.
r r
Aa = A ⋅ ua
(ua = 1)
= Aua cos θ = A cos θ
r r
Aa = A ⋅ ua şeklinde bulunur.
5
• A vektörünün dik bileşeni:
r r
r
r
r r
r
r
A = A⊥ + Aa ⇒ A⊥ = A − Aa = A − ( A cos θ )ua
r r


−1 A ⋅ u a
 → A⊥ = A sin θ veya
θ = cos 

A


2
A⊥ = A2 − Aa ' den bulunur.
ÖRNEK 6
ekilde verilen
F kuvvetinin
AB çubuğuna
paralel ve dik
bileşenlerini
bulunuz.
6
7
Noktasal Cismin Dengesi
Bu bölümde;
Kuvvetleri
bieşenlerine ayırma
ve kartezyen vektör
şeklinde ifade etme
yöntemleri noktasal
cismin dengesini
içeren problemlerin
çözmede
kullanılacaktır.
Bölüm 3
8
Noktasal Cismin Dengesi
• Denge Koşulu: Bir maddesel noktaya etkiyen bütün
kuvvetlerin bileşkesi sıfırsa maddesel nokta dengededir.
• Bir parçacık, başlangıçta hareketsizken halen
durağan halde bulunuyorsa veya başlangıçta
hareketli iken halen sabit hıza sahipse
dengededir.
• “denge” veya “statik denge” ifadesi çoğu zaman
durmakta olan bir nesneyi tanımlamak için
kullanılır.
9
• Denge durumunu korumak için Newton’un birinci hareket
kanununu sağlamak gereklidir: bir parçacık üzerine etkiyen
bileşke kuvvet sıfır ise, parçacık dengededir.
r
∑F = 0
• Bu formül denge için gerekli koşul olmakla kalmayıp, aynı
zamanda yeterli koşuldur. Bu durum Newton’un ikinci
hareket kanunu ile ortaya konur.
r
r
∑ F = ma
r
r
⇒ ma = 0 ⇒ a = 0
• Parçacık sabit hızla hareket etmekte veya durmaktadır
10
Serbest Cisim Diyagramı
• Denge denklemini doğru uygulayabilmek için, parçacık
üzerine etkiyen tüm bilinen ve bilinmeyen kuvvetleri
hesaba katmak gerekir. Bunun için parçacığı
çevresinden soyutlanmış ve serbest olarak gösteren bir
şema çizilir.
• Parçacık üzerine etkiyen tüm kuvvetleri gösteren bu
çizime “serbest cisim diyagramı” denir.
• Serbest cisim diyagramını çizerken kullanılan iki bağlantı
tipi :
– Yaylar
– İpler ve makaralar
11
Yaylar
• Mesnet olarak lineer elastik bir yay
kullanılıyorsa, yayın uzunluğu, üzerine etkiyen
kuvvet ile doğru orantılı olarak değişir.
• Yayların elastikliğini tanımlayan : yay sabiti (k)
F = ks
s = l − l0
l0 = 0.4 m k = 500 N / m l = 0.6 m l = 0.2 m
F = ks = (500 N / m)(0.6m − 0.4m) = 100 N
F = ks = (500 N / m)(0.2m − 0.4m) = −100 N
12
İpler (Kablolar) ve Makaralar
• Tüm kabloların ihmal
edilebilir bir ağırlığa sahip ve
uzayamaz olduğu kabul
edilecektir.
• Kablolar sadece çekme
kuvveti taşırlar ve bu kuvvet
daima kablo doğrultusunda
etki eder.
• ekilde herhangi bir θ
açısında, kablo uzunluğu
boyunca sabit T gerilmesi
oluşmaktadır.
13
Serbest Cisim Diyagramı Çizme Yöntemi
Öncelikle yapılması gereken;
Uygun bir parçacık belirlendikten sonra buna etkiyen
kuvvetleri gösterebileceğimiz serbest cisim
diyagramını basit bir şekilde çizmektir.
14
• 1.adım: parçacık çevresinden soyutlanarak, serbest kaldığı
düşünülerek genel hatlarıyla çizilir.
• 2.adım: parçacık üzerine etkiyen bütün kuvvetler gösterilir. Bu
kuvvetler cismi hareket ettirmeye çalışan “aktif kuvvetler”
ve/veya hareketi önleme eğilimi olan kısıtlamalar ve
mesnetlerin neden olduğu “tepki (reaktif) kuvvetleri”dir.
• 3.adım: bilinen kuvvetler uygun büyüklük (şiddet) ve
doğrultularla (yön) işaretlenmelidir. Bilinmeyen kuvvetlerin
şiddet ve yönü ise harfle gösterilir.
• ∗ Bir kuvvetin etki çizgisi biliniyor, ancak yönü ve şiddeti
bilinmiyorsa, kuvvet yönünü tanımlayan “ok ucu” varsayıma
göre seçilir. Doğru yön şiddet bulunduktan sonra işaretlenir.
Tanım gereği şiddet daima pozitiftir, çözüm negatif bir skaler
verirse eksi işareti kuvvetin ucunun veya yönünün başta
varsayılanın tersi yönde olduğunu gösterir.
15
Örnek 7
• C noktasının serbest cisim
diyagramını çiziniz.
16
Düzlemsel Kuvvet Sistemleri
r
∑F =0 →
∑F
x
=0
∑
• x-y düzleminde bulunan
kuvvetlerin dengede olması
için vektörel toplamın “sıfır”
olması gerekir.
• Bu vektörel denklemin
sıfıra eşit olması için x ve y
bileşenleri sıfıra eşit
olmalıdır.
• Bu iki denklem en çok iki
bilinmeyen kuvvetin
bulunması için kulanılır.
Fxiˆ + Fy ˆj = 0 • Denklemlerde kuvvetlerin
yönleri de dikkate
alınmalıdır.
F =0
∑
∑
y
17
Skaler gösterim
• Bileşenlerin gösteriminde skaler notasyon kullanılacaktır.
Her bir bileşenin yönü serbest cisim diyagramında
bileşenin ok yönüne karşı gelen bir cebirsel işaret ile
ifade edilir. Bir kuvvet bileşeninin işareti bilinmiyorsa,
alınan yön pozitif olur, çözüm negatif çıkarsa kuvvet
yönünün ters olduğu anlaşılır.
• Örneğin,
∑F
x
= 0 → + F + 10 = 0 → F = −10 N
18
Örnek 8
• D silindiri 60 kg’dır. BA ve BC
kablolarında oluşan çekme
kuvvetlerini bulunuz.
19
20
Örnek 9
•
8 kg’lık lambanın şekildeki
gibi taşınabilmesi için AC
kablosunun uzunluğu ne
olmalıdır?
• l’AB=0.4 m (deforme
olmamış boy)
21
22
Ödev 7
W
• ekilde gösterilen
kablolarda 0.5 kN’un
üzerinde çekme
kuvveti oluşmaması
için asılı olan kovanın
ağırlığını (W)
bulunuz.
23
Üç Boyutlu Kuvvet Sistemleri
• Parçacık dengesinin
sağlanması için:
• Parçacık üzerine etkiyen
kuvvetler i, j, k bileşenlerine
ayrılırsa:
Bu denklemler, parçacığa etkiyen x, y, z kuvvet
bileşenlerinin cebirsel toplamlarını göstermektedir, “0”dır.
Bu denklemler ile en fazla 3 bilinmeyen kuvvet
bulunabilir.
24
Örnek 10
40 N’luk sandığı taşımak için kullanılan
kablolarda oluşan kuvvetleri bulunuz.
25
26
Kuvvet Sistemleri
• Bir kuvvetin bir nokta veya eksene göre momentinin
bulunması
• Bir noktadan geçmeyen kuvvet sistemlerinin
bileşkelerinin bulunması
• Kuvvet çiftinin oluşturduğu momentin bulunması
• İki ve üç boyutlu kuvvetler için moment hesaplanması
• Moment bir cismi döndürmeye çalışır, denge ise cismin
dönmemesini gerektirir.
• Bir cisme bir kuvvet uygulandığında, cismi etki çizgisinin
dışında bir nokta etrafında döndürmeye çalışır. Bu
döndürme eğilimine “tork” veya daha sık kullanıldığı
şekliyle “moment” denir.
27
Bir kuvvetin momenti
• Bir kuvvetin bir noktaya veya bir
eksene göre momenti (M), kuvvetin
cismi o nokta veya eksen etrafında
döndürme eğiliminin bir ölçüsünü
gösterir.
M0 = F . d
• Momentin şiddeti, F kuvvetinin
şiddeti ile orantılıdır ve F kuvvetine
dik olan moment kolu d ile
orantılıdır.
• (b)’de moment kolu daha kısa !
d’=dsinθ
(d’<d)
• (c)’de θ=0 d’=0 M=0
28
• Moment daima F ve d’yi içeren
düzleme dik bir eksen etrafında
etkimektedir. Ve bu eksen düzlemi,
“O” noktasında kesmektedir.
• iddeti “M0 = F . d ” olan momentin
doğrultusu sağ el kuralı kullanılarak
belirlenir.
29
Bileşke Moment
• Bir kuvvet sistemi x-y
düzleminde yer alırsa, her
bir kuvvetin O noktasına
göre momenti z ekseni
yönünde olacaktır.
• Sistemin bileşke momenti,
bütün kuvvetlerin
momentlerinin cebirsel
toplamı alınarak
bulunabilir, çünkü bütün
moment vektörleri aynı
doğrultudadır.
• Moment saatin tersi yönündeyse (+), saat yönündeyse (-)
• Sağ el kuralına göre baş parmak sayfa düzleminin dışına
doğru (+z ekseni) ise (+), içine (-z ekseni) doğruysa (-) 30
Örnek 11
31
Örnek 12
Etkiyen dört kuvvetin O noktasında
oluşturduğu bileşke momentin
değerini bulunuz.
Pozitif moment yönü, +k yönünde,
yani saatin tersi yönünde olduğu
kabulü ile:
32
• F kuvveti her zaman dönme
etkisi yaratmayabilir. F
kuvveti A noktasında
MA=F.dA momenti kadar
döndürmeye çalışıyor, ancak
gerçek döndürme etkisi B
mesnetinin kaldırılması
halinde oluşur.
• Çiviyi çıkarmak için FH
kuvvetinin O noktasında
yaratmış olduğu momentin,
FN çivi kuvvetinin yaratmış
olduğu momentten büyük
olması gerekir.
33
Vektörel çarpım (çapraz çarpım)
• Bir kuvvetin momenti, kartezyen vektörler kullanılarak
ifade edilebilir. Bundan önce vektör çarpımında
kullanılacak olan çapraz çarpıma bakalım. A ve B
vektörlerinin vektörel (çapraz) çarpımı sonucu C
vektörü elde edilir.
r r r
C = A× B
• C vektörünün şiddeti de şu şekilde bulunabilir:
C = AB sin θ
34
• YÖN: C vektörünün yönü,
A ve B vektörlerinin
bulunduğu düzleme diktir.
Sağ el kuralı ile belirlenir.
• Parmaklarımızı A’dan B’ye
doğru kıvırdığımızda
başparmağımızın gösterdiği
yön C vektörünün yönünü
gösterir.
• C vektörünün yönü,
uc birim vektörüyle
karakterize edilebilir.
r r r
r
C = A × B = ( AB sin θ ) uc
35
Vektör çarpım kuralları
asosiyatif özellik
her durumda şiddet aynı
doğrultu aynı
Distributif özellik
36
Kartezyen vektör formülasyonu
• Kartezyen birim vektörlerinin
çapraz çarpımlarını bulmak için:
• A ve B vektörlerinin vektörel çarpımı :
• Bu terimler düzenlenirse :
37
Kartezyen vektör formülasyonu
• Vektörel çarpım, determinant formunda
da ifade edilebilir. Bu determinant (3
satır ve 3 kolona sahip) üç minör
kullanılarak hesaplanır.
Determinant hesabı için minörlerin bulunması
Bu üç
bileşen
toplanır ve
determinant
bulunur :
38
Bir kuvvetin momenti: Vektör formülasyonu
Bir kuvvetin bir noktaya göre momenti
r
r r
M0 = r × F
O noktasında F kuvvetinin etki çizgisinin
herhangi bir yerine olan pozisyon vektörü
Vektörel çarpım ile belirlenen moment doğru
şiddet ve doğru yöne sahip olacaktır.
39
iddet
r
r r
M0 = r × F
⇒ M 0 = rF sin θ = F (r sin θ ) = Fd
θ = r ve F vektörleri arasındaki açı
d = dik mesafe
Yön
Sağ el kuralına göre
momentin yönü belirlenir.
40
Taşınabilirlik (Transmisibilite) ilkesi
Vektörel çarpım işlemi,
üç boyutlu problemlerde
sıklıkla kullanılır. Çünkü
kuvvetin etki çizgisinden
O noktasına olan dik
mesafeyi bulmaya gerek
yoktur. O noktasından F
kuvvetinin etki çizgisinin
herhangi bir yerine
ölçülen r vektörü
moment hesabı için
kullanılabilir.
r
r r r r r r
M 0 = r1 × F = r2 × F = r3 × F
F kuvveti etki çizgisinin
herhangi bir yerine
etkiyebilir, ve O
noktasında aynı
moment etksini yaratır.
41
Momentin kartezyen vektör formülasyonuna göre
bulunması
+
−
+
Konum vektörü bileşenleri
Kuvvet vektörü bileşenleri
42
•
Bir kuvvet sisteminin bileşke momenti
r
r r
Bir kuvvet sisteminin O
M r 0 = ∑ ri × Fi
noktasına göre bileşke
momenti şöyle bulunur:
i
43
Örnek 13
• O noktasında oluşan
moment değerini ve
yönünü bulunuz.
44
45