Kapasite Endüktans

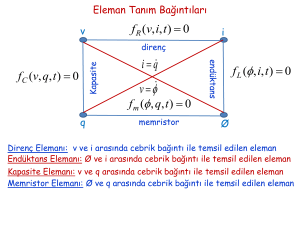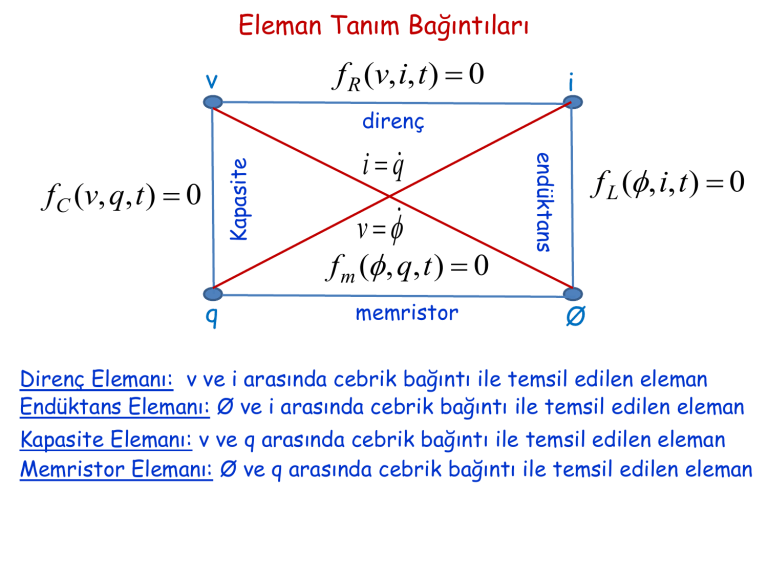
Eleman Tanım Bağıntıları
f R (v, i, t )  0
v
i
fC (v, q, t )  0
q
i  q
v  
f m ( , q, t )  0
memristor
endüktans
Kapasite
direnç
f L ( , i, t )  0
Ø
Direnç Elemanı: v ve i arasında cebrik bağıntı ile temsil edilen eleman
Endüktans Elemanı: Ø ve i arasında cebrik bağıntı ile temsil edilen eleman
Kapasite Elemanı: v ve q arasında cebrik bağıntı ile temsil edilen eleman
Memristor Elemanı: Ø ve q arasında cebrik bağıntı ile temsil edilen eleman
2-uçlu Kapasite ve Endüktans Elemanları
Lineer ve Zamanla Değişmeyen
Kapasite
Endüktans
di (t )
dt
d (t )
di (t )
L
dt
dt
dv(t )
dt
dq (t )
dv(t )
C
dt
dt
i (t )  C
v(t )  L
Zamanla Değişmeyen
Lineer olmayan ve zamanla değişenleri ifade edebilmek için akı ( ) ve yük
(q ) kullanılır:
t
q(t ) ˆ  i ( )d

t
[C]
 (t ) ˆ  v( )d [Wb]

L.O. Chua, C.A. Desoer, S.E. Kuh. “Linear and Nonlinear Circuits” Mc.Graw Hill, 1987, New York
Kapasite
f C ( q, v )  0
yük kontrollü
v  vˆ( q )
gerilim kontrollü
q  qˆ (v)
qˆ (v ) türetilebilir bir
fonksiyon ise
dq
d (qˆ (v)) dv
ˆ i 
dt
dv dt
dv C (v) ˆ dqˆ (v)
i  C (v )
dv
dt
Endüktans
f L ( , i)  0
akı kontrollü
i  iˆ( )
akım kontrollü
  ˆ(i )
ˆ(i ) türetilebilir bir
fonksiyon ise
d
d (ˆ(i )) di
ˆ v 
dt
di dt
dˆ(i )
di
v  L(i )
L(i ) ˆ
di
dt
Kapasite
Lineer Zamanla Değişmeyen
Endüktans
Lineer Olmayan Zamanla Değişmeyen
L.O. Chua, C.A. Desoer, S.E. Kuh. “Linear and Nonlinear Circuits” Mc.Graw Hill, 1987, New York
Kapasite
Lineer Zamanla Değişen
q(t )  C (t )v(t )
dv(t ) dC (t )
i (t )  C (t )

v(t )
dt
dt
q(t )  (2  sin t )v(t )
C (t )  2  sin t
Endüktans
 (t )  L(t )i(t )
v(t )  L(t )
di (t ) dL(t )

i (t )
dt
dt
 (t )  (2  sin t )i(t )
L(t )  2  sin t
di (t )
dv(t )
v
(
t
)

(
2

sin
t
)
 (cos t )i (t )
i (t )  (2  sin t )
 (cos t )v(t )
dt
dt
L.O. Chua, C.A. Desoer, S.E. Kuh. “Linear and Nonlinear Circuits” Mc.Graw Hill, 1987, New York
Zamanla Değişmeyen Lineer Kapasite
ve
Endüktans Elemanlarının Özellikleri
Kapasite
Bellek Özelliği
t
1
v(t )   i ( )d
C 
v (t ) sadece i (t ) ‘ye değil, i ( ) ‘nun
     t aralığındaki tüm
geçmiş değerlerine de bağlı
     t0
t
v(t0 )
1
v(t )  v(t0 )   i ( )d , t  t0
Ct
0
Endüktans
t
1
i (t )   v( )d
L 
i (t ) sadece v (t ) ‘ye değil,v ( ) ‘nun
     t aralığındaki tüm
geçmiş değerlerine de bağlı
     t0
i (t0 )
t
1
i (t )  i (t0 )   v( )d , t  t0
Lt
0
v(t0 ) ilk koşul, geçmiş i ( ) ,     t v(t0 ) ilk koşul, geçmiş v ( ),      t
değerlerinin v (t ) ‘ye etkisini veriyor. değerlerinin i (t ) ‘ye etkisini veriyor.
Kapasite
Süreklilik Özelliği
iC (t ), [ta , tb ] aralığında sınırlı
değerler alıyorsa, kapasite
gerilimi vC (t ), (ta , tb )
aralığında sürekli bir fonksiyondur.
ta  T  tb
vC (T  )  vC (T  )
Endüktans
vL (t ), [ta , tb ] aralığında sınırlı
değerler alıyorsa, kapasite
gerilimi iL (t ) , (ta , tb )
aralığında sürekli bir fonksiyondur.
ta  T  tb
iL (T  )  iL (T  )
L.O. Chua, C.A. Desoer, S.E. Kuh. “Linear and Nonlinear Circuits” Mc.Graw Hill, 1987, New York
Kayıpsızlık Özelliği
Tanım: (Enerji)
[t1, t2 ] aralığında bir elemana aktarılan toplam enerji w(t1, t2 ) [Joules] ‘dur.
t2
w(t1, t2 ) 
ˆ  v(t )i (t )dt
t1
Kapasite
Yük kontrollü kapasite elemanına
ilişkin enerji kapasite gerilimi veya
yük fonksiyonundan bağımsızdır. t1
ve t 2 anlarındaki yük değerleri ile
belirlenir.
t2
dq
wC (t1, t2 )   v(q)
dt
dt
t
1
wC (q1, q2 ) 
q2
 v(q)dq
Endüktans
Akı kontrollü endüktans elemanına
ilişkin enerji endüktans akımı veya
akı fonksiyonundan bağımsızdır. t1
ve t 2 anlarındaki akı değerleri ile
belirlenir.
t2
d
wL (t1, t2 )   i ( )
dt
dt
t
1
wL (1, 2 ) 
vC ( q ) 
q
C
 i( )d
1
q1
Örnek:
2
iL ( ) 

L
sonuç
Kapasite
Periyodik bir fonksiyon ile
uyarıldığında, yük kontrollü
kapasiteye ilişkin enerji bir
peryod boyunca sıfırdır
1
1
2
WC (Q ) 
Q  CV 2
2C
2
Bir kapasiteden alınabilecek
maksimum enerji miktarı
Endüktans
Periyodik bir fonksiyon ile
uyarıldığında, yük kontrollü
kapasiteye ilişkin enerji bir
peryod boyunca sıfırdır
1 2 1
WL ( ) 
  LI 2
2L
2
Bir endüktanstan alınabilecek
maksimum enerji miktarı
1. Mertebeden Lineer Devreler
RTH iC  vC  vTH E.T.B+KGY
dvC
iC  C
 CvC
dt
vC
vTH

vC  

RTH C RTH C
E.T.B+KAY GN vL  iL  iN
diL
 LiL
dt
i
i
iL   L  N
GN L GN L
vL  L
Durum Denklemleri, Kalman (1960)
x  ax  bu,
x(0)  x0
L.O. Chua, C.A. Desoer, S.E. Kuh. “Linear and Nonlinear Circuits” Mc.Graw Hill, 1987, New York
1. Mertebeden Diferansiyel Denklem Çözümü
x  ax
dx
 ax
dt
x(0)  x0
x (t )

C
t
dx
  adt
x
0
Inx (t )  InC  at
x(t )
In
 at
C
x(t )  Ceat
t
x (0)  Cea 0
x(t )  eat x0
x  ax  u
x(0)  x0
varsayım: x(t )  S (t )e at
d
( S (t )e at )  a ( S (t )e at )  u(t)
dt
dS(t) at
at
aS (t )e 
e  aS (t )e at  u(t)
dt
t
dS(t) at
e  u(t)
dt
dS(t)
 e  atu(t)
dt
varsayım: x(t )  S (t )e
at
t
S (t )   e  a u()d  S (0)
0
t
x(t )  S (0)e at   e a (t  )u ( ) d ,
0
0
0
x(0)  S (0)e a 0   e a (t  )u ( )d ,
0
t
x(t )  e at x(0)   e a (t  )u ( ) d
0
t
x(t )  e at x(0)   e a (t  )u ( ) d
öz çözüm
0
zorlanmış çözüm
t
t
Durum Denkemlerinin Elde Edilmesi
I- İki uçlu direnç, endüktans, kapasite bağımsız akım ve gerilim
kaynaklarının oluşmuş devrelerde durum denklemlerinin elde edilmesi
Amaç:
x  Ax  Bu
y  Cx  Du ,
x (0)  x0
x  Rn durum değişkenleri - kapasite gerilimleri, endüktans akımları
y  R r çıkış büyüklükleri
- ilgilenilen eleman akımları ve gerilimleri
u  R p giriş büyüklükleri
- bağımsız akım kaynağının akımı ve bağımsız
gerilim kaynaklarının gerilimleri
Yöntem:
1. Adım: Uygun Ağaç Seçimi
a-) gerilim kaynaklarını dal elemanı olarak seçiniz, ağaç
tamamlanmamışsa (b)’ye geçiniz
b-) kapasiteleri dal elemanı olarak seçiniz, ağaç tamamlanmamışsa
(c)’ye geçiniz
c-) dirençleri dal elemanı olarak seçiniz, ağaç tamamlanmamışsa
(d)’ye geçiniz
c-) endüktansları dal elemanı olarak seçiniz
2. Adım: Durum değişkenlerini belirleme
Dallardaki kapasite gerilimleri, kirişlerdeki endüktans akımları
durum değişkenleridir.
Durum değişkenlerini belirleyiniz ve uç denklemlerini yazınız.
C
dvc (t )
 ic (t )
dt
L
3. Adım: Durum denklemlerini yazma
diL (t )
 vL (t )
dt
Lineer bağımsız akım denklemlerini yazınız
(Temel kesitlemelere ilişkin denklemler)
Lineer bağımsız gerilim denklemlerini yazınız
(Temel çevrelere ilişkin denklemler)
Yazdığınız denklemlerden yararlanarak dallardaki kapasitelerin
akımları ile kirişlerdeki endüktansların gerilimlerini, durum
değişkenleri ve girişler cinsinden belirleyiniz.
Hangi devre büyüklüklerine karşı
gelmekteler.