Deney No
Deneyin Adı
Deneyin Amacı
: M4
: MAXWELL TEKERLEĞİ
Teorik Bilgi
:
: İzole sistemlerde enerjinin korunumu ilkesini ve potansiyel ile kinetik
enerji arası dönüşümlerini gözlemlemek/türetmek
Maxwell tekerleği deneyi potansiyel enerji ile lineer kinetik enerji ve dönme kinetik
enerjisi arasındaki dönüşümleri incelemek için gerçekleştirilir. Fiziksel olguları çevre ile
etkileşimlerine göre; izole ve izole-olmayan sistemler olarak sınıflayabiliriz. İzole-olmayan
sistemlerde, sistem içerisine ve dışarısına enerji transferi olmaktadır, fakat izole sistemlerde
böyle bir enerji transferi gerçekleşmez. Bundan dolayı izole sistemlerde toplam enerji
korunmaktadır.
Enerji farklı formda bulunabilir (örneğin; mekanik, ısı, nükleer, kimyasal, ışıma, elektrik,
vb...) ve bu formlar birbirlerine dönüşebilir. Örneğin, buhar makinaları ısı enerjisini mekanik
enerjiye, atom reaktörleri nükleer enerjiyi mekanik enerjiye oradan da elektrik enerjisine,
dinamolar ve hidroelektrik santraller ise mekanik enerjiyi elektrik enerjisine dönüştüren
sistemlerdir.
Bu örneklerden hidroelektrik santralleri ele alalım. Bir baraj kapağını çok kısa bir süre
açıp hemen kapatır ve zamanı durdurup sistemi incelersek (t=0) belirli bir h yüksekliğinde bir
miktar su hareketsiz durmakta, sudan h mesafe aşağıda ise türbinler hareketsiz durmaktadır. Bu
durumda aşağıdaki bulunan türbine göre h yükseklikteki suyun belirli bir potansiyel enerjisi
vardır. Zamanı ilerletip, su türbine ulaşmadan tekrar durduralım (t=t1). Bu durumda su belirli
bir mesafe kat etmiş (h=x) ve sahip olduğu potansiyel enerjinin bir kısmı artık hareket enerjisine
yani kinetik enerjiye dönüşmüştür. Tribünler hala hareketsiz şekilde durmaktadır. Bu durumda
sistemde hiç enerji kaybı olmadığına göre (sürtünmeler ihmal edilmektedir) toplam enerjinin
sabit kalması gerekmektedir. Zaman tekrar ilerletilip tribünlerin dönme anı incelenir ise (t > t1),
artık suyun bütün potansiyel enerjisinin kinetik enerjiye dönüştüğü, bu kinetik enerjinin de
tribünlere aktarılarak tribünlere bir dönme kinetik enerjisi kazandırdığı görülür. Maxwell
tekerleği işte bu üç tür enerjinin dönüşümünü inceleyen bir deney sistemidir.
Deney düzeneğinde, merkezinden bir mil geçirilmiş katı bir disk kullanılır. Mil, her iki
ucunda bulunan iplerle asılı durumdadır. İplerin mile sarılması ile disk belirli bir yüksekliğe
çıkartılır ve serbest bırakılır. İlk hızı olmadan serbest bırakılan disk kendi ekseni etrafında
dönerek aşağı doğru düşer. Mile sarılı ip tamamen açıldıktan sonra (denge konumu) diskin
dönmesi sayesinde ters yönde tekrar mil üzerine sarılmaya başlar ve disk bu sefer yukarı doğru
hareket eder. Sürtünme ihmal edilecek olursa toplam enerjinin korunumu ilkesi sebebiyle bu
1
disk dönerek ilk konumuna yükselecek ve bu hareketini periyodik olarak sonsuza ya da bir
müdahale olana kadar sürdürecektir. Bu sistemi detaylı bir şekilde inceleyecek olursak:
Diskin en yüksek pozisyonda (milin tamamen sarılı) bulunduğu durumu x=h, denge
konumunu (ipin tamamen açık) ise x=0 olarak alalım. Disk x=h konumunda bulunurken (t=0)
sistemin toplam enerjisi;
𝐸 = 𝑚𝑔𝑥 = 𝑚𝑔ℎ
(8.1)
olur. Burada m disk ve milin toplam kütlesidir.
Disk serbest bırakıldığında aşağı doğru düşer ve mile sarılı ipin açılması sebebiyle kendi
etrafında dönmeye başlar. Bu durumda artık sistemde, hem değişen yükseklikten (x=hx) dolayı
bir potansiyel enerji farkı, hem aşağı doğru hareketten (vx) kaynaklı bir lineer kinetik enerji
(EKL), hem de diskin dönmesinden (ωx) kaynaklı bir dönme kinetik enerjisi (EKR) vardır. Kısaca
sistemin ilk durumda sahip olduğu potansiyel enerji artık kinetik enerjiye dönüşmektedir.
Sistemde sürtünme ihmal edilirse toplam enerji korunacaktır. Dolayısıyla toplam enerji ilk
duruma eşit olmalıdır. Bu enerjileri ve toplam enerjiyi yazacak olursak;
1
𝐼𝜔𝑥 2
2
1
1
= 𝑚𝑔ℎ𝑥 + 𝑚𝑣𝑥 2 + 𝐼𝜔𝑥 2 = 𝑚𝑔ℎ
2
2
𝐸𝑝 = 𝑚𝑔ℎ𝑥 , 𝐸𝐾𝐿 =
𝐸 = 𝐸𝑝 + 𝐸𝐾𝐿 + 𝐸𝐾𝑅
1
𝑚𝑣𝑥 2
2
,
𝐸𝐾𝑅 =
(8.2)
(8.3)
olur.
Diskin hareketine devam edip denge konumuna ulaştığı durumu inceleyecek olursak;
yükseklik x=0 olmuş lineer ve dönme hızları maksimum değerine ulaşmış olur. Fakat ip
tamamen açıldıktan sonra ters yönde sarılmaya başlar ve disk yükselir. Bu anda artık sistemin
sahip olduğu kinetik enerji potansiyel enerjiye dönüşmeye başlar.
𝐸𝑝 = 𝑚𝑔0 = 0 , 𝐸𝐾𝐿 =
𝐸 = 𝐸𝑝 + 𝐸𝐾𝐿 + 𝐸𝐾𝑅 =
1
𝑚𝑣 2
2
,
𝐸𝐾𝑅 =
1 2
𝐼𝜔
2
1
1
𝑚𝑣 2 + 𝐼𝜔2 = 𝑚𝑔ℎ
2
2
(8.4)
(8.5)
Eğer sistem tekrar x=hx yüksekliğine ulaştığında durumu incelersek, sitemin enerjisi (8.3)
ile , sistem x=h yüksekliğine ulaştığında ise (8.1) ile ifade edilecektir.
2
Disk x=hx yüksekliğinden geçerken bir şekilde diskin dönme periyodunu ölçebilseydik
yapabileceğimiz hesapları inceleyelim. (8.3) numaralı denklem tekrar düzenlenirse;
1
1
𝑚𝑣𝑥 2 + 𝐼𝜔𝑥 2 = 𝑚𝑔(ℎ − ℎ𝑥 )
2
2
1
1
(ℎ − ℎ𝑥 ) = 𝑥 , 𝑚𝑔𝑥 = 𝑚𝑣𝑥 2 + 𝐼𝜔𝑥 2
2
2
(8.6)
(8.7)
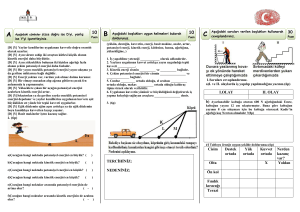
Burada ω diskin açısal hızıdır ve ipin mil etrafında açılması/sarılması ile oluşur.
𝑑𝑥⃗ = 𝑑𝜃⃗ × 𝑟⃗
⃗⃗
𝑥
⃗⃗
⃗⃗ 𝑑𝜃
𝑑𝑥
⃗⃗⃗⃗ × 𝑟
⃗⃗
=
× 𝑟⃗⃗ ≡ 𝜔
𝑑𝑡 𝑑𝑡
𝑣 = 𝜔. 𝑟
𝑣
𝜔=
𝑟
⃗⃗ ≡
𝑣
𝑟⃗⃗
𝑑𝑥⃗
(8.8)
(8.9)
(8.10)
(8.11)
𝑑𝜃⃗
Şekil 8.1
Burada r milin çapıdır. Bu durumda toplam enerji denklemi;
𝑣𝑥 2
𝐼
(𝑚 + 2 )
2
𝑟
(8.12)
𝑣𝑥 2
𝐼
(1 +
)
2
𝑚𝑟 2
(8.13)
𝑚𝑔𝑥 =
𝑔𝑥 =
olur.
Kendi ekseni etrafında dönen iç içe iki diskten oluşan sistemin eylemsizlik momenti, her
birisinin eylemsizlik momentine eşittir. Bu durumda iki diskin toplam eylemsizlik momentini
yaklaşık olarak şu şekilde alabiliriz (R diskin yarıçapı);
𝐼 = 𝐼𝑑𝑖𝑠𝑘 + 𝐼𝑚𝑖𝑙 =
1
1
1
𝑚𝑚𝑖𝑙 𝑟 2 + 𝑚𝑑𝑖𝑠𝑘 𝑅 2 ≅ 𝑚𝑅 2
2
2
2
3
(8.14)
Burada m toplam kütleye eşittir. Bu durumda (8.13) ve (8.14) kullanılarak, diskin x
noktasından geçerken sahip olduğu yaklaşık hız şu şekilde hesaplanabilir;
𝑔𝑥 =
𝑣𝑥 2
𝑅2
(1 + 2 )
2
2𝑟
𝑣𝑥 = √
(8.15)
2𝑔𝑥
𝑅2
(1 + 2 )
2𝑟
(8.16)
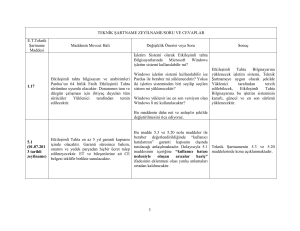
Deneyin Yapılışı:
Şekil 8.2
Deney düzeneğini şekildeki gibi kurunuz. İp tamamen açık durumda iken bir su terazisi
yardımıyla diskin yatay düzlemle paralelliğini kontrol ediniz, gerekiyorsa ayarlayınız.
Diskin (R) ve milin (r) çaplarını ölçerek yarıçaplarını hesaplayınız ve kaydediniz.
R =............
r =............
4
Sensörü olabilecek en büyük yüksekliğe çıkartarak sabitleyiniz. Diski en üst pozisyona
kadar sarınız ve bu durumda diskin kütle merkezi ile sensörün orta noktası arası yükseklik
farkını (x=h-hx) ölçerek kaydediniz.
x1 =............
Ölçüm cihazından sensörü başlatınız ve diski ilk hızsız ve yalpa yapmayacak şekilde
dikkatlice serbest bırakınız. Sensör, diskin üzerinde bulunan bir yarığın, kendisinden sonra
gelen yarığın konumuna ulaşması için geçen süreyi ölçer (ΔT) . Disk üzerinde 36 adet yarık
bulunduğu için bu süre diskin tam bir tur yapması için geçen sürenin (periyot (T)) 1/36’sı
dır. Bu değeri kaydedin ve periyodu hesaplayın.
(not: her ölçümü 3 kere tekrar edin ve ortalamasını alın)
ΔT1=............
T1 =............
Sensörü iki farklı x değerine ayarlayınız ve aynı ölçümleri tekrar ediniz.
x2 =............
ΔT2=............
T2 =............
x3 =............
ΔT3=............
T3 =............
Periyot bir tam tur için geçen süredir, bir tam turun ise açı cinsinden 2π olduğunu
bildiğimize göre, ortalama açısal hızı
𝜔=
2𝜋
𝑇
(8.17)
5
şeklinde yazabiliriz. Lineer hız ile açısal hız arasındaki bağıntı ise daha önce formül (8.11) ile
verilmişti. Bu iki formülü (8.11), (8.17) kullanarak her farklı yükseklik değeri için lineer hızları
hesaplayınız.
v1D =...............
v2D =...............
v3D =...............
Bu hesaplanan hız değerleri deneysel yollarla elde edilmiş değerlerdir. Teorik kısımda ise
kütlesi ve çapı bilinen bir diskin belirli bir yükseklikten geçerken hangi hıza sahip olacağını
bulmuştuk. Bu formülü (8.16) kullanarak her üç yükseklik için beklenen hız değerlerini
hesaplayınız.
v1T =...............
6
v2T =...............
v3T =...............
Bulduğunuz bu hız değerlerinin bağıl hatalarını (Δv) hesaplayınız ve bütün değerleri tabloya
kaydediniz.
Bulduğunuz hız değerlerinin yüksekliğe göre değişimini bir grafik üzerinde gösteriniz
(Teorik değerleri uygun bir biçimde birleştirerek, deneysel değerleri ise sadece veri
noktaları olarak).
Δv1 =...............
Δv2 =...............
Δv3 =...............
Tablo 8.1
x (m)
ΔT (s)
T (s)
ω (R/s)
7
vD (m/s)
vT (m/s)
Δv (m/s)
Yorum Ve Sonuçlar :
(İpuçları: Deneyde öğrendikleriniz. Olası hatalar ve sebepleri. Detaylı açıklayınız. Deneyi
özetleyiniz)
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………………………………………………………
…………………………………………………...………………………………………………
…………………………...………………………………………………………………………
…...…………………………………………………………………………...…………………
………………………………………………………...…………………………………………
………………………………...…………………………………………………………………
………...…………………………………………………………………………...……………
……………………………………………………………...……………………………………
8
Sorular :
1) Deneyde sürtünmeden kaynaklı bir enerji kaybı vardır. Bunu hesaplamak istesek toplam
enerji formüllerinde (bkz. teorik bilgi) nasıl değişiklikler yapmalıyız. Yeni Formülü
türetiniz.
2) Teorik bilgide verilen baraj örneği için her üç duruma ait toplam enerji denklemlerini
türetiniz. (t=0 ; suyun en tepede olduğu an, t=t1 ; suyun belirli bir yükseklikten düşmüş
ama türbine ulaşmadığı durum ve t=t3 ; suyun türbine çarpıp türbinin döndüğü durum.)
……………………………………………………………………………………………...……
………………………………………………………………………………………...…………
…………………………………………………………………………………...………………
……………………………………………………………………………...……………………
………………………………………………………………………...…………………………
…………………………………………………………………...………………………………
……………………………………………………………...……………………………………
………………………………………………………...…………………………………………
…………………………………………………...………………………………………………
……………………………………………...……………………………………………………
………………………………………...…………………………………………………………
…………………………………...………………………………………………………………
……………………………...……………………………………………………………………
………………………...…………………………………………………………………………
…………………...………………………………………………………………………………
……………...……………………………………………………………………………………
………...…………………………………………………………………………………………
…...……………………………………………………………………………………………...
……………………………………………………………………………………………...……
………………………………………………………………………………………...…………
…………………………………………………………………………………...………………
……………………………………………………………………………...……………………
………………………………………………………………………...…………………………
…………………………………………………………………...………………………………
……………………………………………………………...……………………………………
………………………………………………………...…………………………………………
…………………………………………………...………………………………………………
……………………………………………...……………………………………………………
………………………………………...…………………………………………………………
…………………………………...………………………………………………………………
……………………………...……………………………………………………………………
………………………...…………………………………………………………………………
…………………...………………………………………………………………………………
……………...……………………………………………………………………………………
………...…………………………………………………………………………………………
…...……………………………………………………………………………………………...
9
……………………………………………………………………………………………...……
………………………………………………………………………………………...…………
…………………………………………………………………………………...………………
……………………………………………………………………………...……………………
………………………………………………………………………...…………………………
…………………………………………………………………...………………………………
……………………………………………………………...……………………………………
………………………………………………………...…………………………………………
…………………………………………………...………………………………………………
……………………………………………...……………………………………………………
………………………………………...…………………………………………………………
…………………………………...………………………………………………………………
……………………………...……………………………………………………………………
………………………...…………………………………………………………………………
…………………...………………………………………………………………………………
……………...……………………………………………………………………………………
………...…………………………………………………………………………………………
…...……………………………………………………………………………………………...
……………………………………………………………………………………………...……
………………………………………………………………………………………...…………
…………………………………………………………………………………...………………
……………………………………………………………………………...……………………
………………………………………………………………………...…………………………
…………………………………………………………………...………………………………
……………………………………………………………...……………………………………
………………………………………………………...…………………………………………
…………………………………………………...………………………………………………
……………………………………………...……………………………………………………
………………………………………...…………………………………………………………
…………………………………...………………………………………………………………
……………………………...……………………………………………………………………
………………………...…………………………………………………………………………
…………………...………………………………………………………………………………
……………...……………………………………………………………………………………
………...…………………………………………………………………………………………
…...……………………………………………………………………………………………...
……………………………………………………………………………………………...……
………………………………………………………………………………………...…………
…………………………………………………………………………………...………………
……………………………………………………………………………...……………………
………………………………………………………………………...…………………………
…………………………………………………………………...………………………………
……………………………………………………………...……………………………………
10