Ortak Varyans ve İstatistiksel Bağımsızlık
Bir rassal değişken çifti istatistiksel olarak bağımsız ise aralarındaki ortak varyansın
değeri “0”dır. Ancak ortak varyans değerinin “0” olması, iki rassal değişkenin
istatistiksel olarak bağımsız oldukları anlamına gelmeyecektir. Zira ortak varyans, iki
rassal değişken arasındaki doğrusal ilişkiyi ölçmek üzere kurgulanmıştır. Şayet iki rassal
değişken arasında doğrusal olmayan bir ilişki varsa, bunun ortak varyans ile tespit
edilebilmesi mümkün değildir.
Örnek 3: Bir araştırmacı dönem sonu sınavları süresince bir araştırma yaparak, günlük
sınav sayısı ile kantinden atıştırma sayısı arasında bir ilişki olup olmadığını tespit etmek
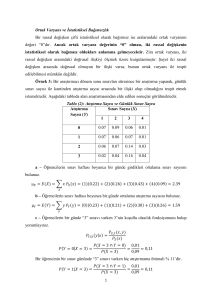
istemektedir. Aşağıdaki tabloda alan araştırmasından elde edilen sonuçlar görülmektedir.
Tablo (2): Atıştırma Sayısı ve Günlük Sınav Sayısı
Atıştırma
Sınav Sayısı (X)
Sayısı (Y)
1
2
3
4
0
0.07
0.09
0.06
0.01
1
0.07
0.06
0.07
0.01
2
0.06
0.07
0.14
0.03
3
0.02
0.04
0.16
0.04
a – Öğrencilerin sınav haftası boyunca bir günde girdikleri ortalama sınav sayısını
bulunuz.
∑
b – Öğrencilerin sınav haftası boyunca bir günde ortalama atıştırma sayısını bulunuz.
∑
c – Öğrencilerin bir günde “3” sınavı varken Y’nin koşullu olasılık fonksiyonunu bulup
yorumlayınız.
Bir öğrencinin bir sınav gününde “3” sınavı varken hiç atıştırmama ihtimali % 11’dir.
1
Bir öğrencinin bir sınav gününde “3” sınavı varken bir kere atıştırma ihtimali % 11’dir.
Bir öğrencinin bir sınav gününde “3” sınavı varken iki kere atıştırma ihtimali % 33’dür.
Bir öğrencinin bir sınav gününde “3” sınavı varken üç kere atıştırma ihtimali % 44’tür.
d – X ve Y arasındaki ortak varyansı bulup yorumlayınız.
Önceki şıklarda
elde edilmiştir. Burada E(XY)
ve
bulunmalıdır.
∑∑
Bu iki rassal değişken arasında pozitif yönlü doğrusal bir ilişki olduğu yorumu
yapılabilir (Unutulmamalıdır ki ilişkinin şiddeti burada değişkenlerin birimlerine bağlıdır.
Bundan dolayı ilişkinin zayıf veya kuvvetli olup olmadığını tespit edemiyoruz).
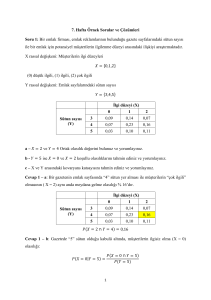
Örnek 4: Aşağıdaki tabloda eldeki kredi kartı (1 – 3) ile bir hafta içerisinde alışveriş
yapma sayıları (0 – 4) arasındaki ortak olasılıkları vermektedir.
Kart Sayısı
(Y)
Tablo (3): Haftalık Alış veriş Sayısı ile Kredi Kartı Sayısı
Haftalık Alışveriş Sayısı (X)
0
1
2
3
4
1
0.08
0.13
0.09
0.06
0.03
2
0.03
0.08
0.08
0.09
0.07
3
0.01
0.03
0.06
0.08
0.08
a – Bir kişi için haftalık ortalama alışveriş sayısı nedir?
∑
2
b – Bir kişinin ortalama kart sayısı nedir?
∑
c – Elinde “2” adet kredi kartı olan bir kişi için haftalık alışveriş sayısının olasılık
fonksiyonunu bulunuz ve yorumlayınız.
İki kredi kartı olan birinin bir hafta içerisinde hiç alışveriş yapmama olasılığı % 8.5’tir.
İki kredi kartı olan birinin bir hafta içerisinde bir kez alışveriş yapma olasılığı %
22.8’dir.
İki kredi kartı olan birinin bir hafta içerisinde iki kez alışveriş yapma olasılığı %
22.8’dir.
İki kredi kartı olan birinin bir hafta içerisinde üç kez alışveriş yapma olasılığı %
25.7’dir.
İki kredi kartı olan birinin bir hafta içerisinde dört kez alışveriş yapma olasılığı %
20’dir.
d - X ve Y arasındaki ortak varyansı bulup yorumlayınız.
Önceki şıklarda
elde edilmiştir. Burada E(XY)
ve
bulunmalıdır.
3
∑∑
Bu iki rassal değişken arasında pozitif yönlü doğrusal bir ilişki olduğu yorumu
yapılabilir (Unutulmamalıdır ki ilişkinin şiddeti burada değişkenlerin birimlerine bağlıdır.
Bundan dolayı ilişkinin zayıf veya kuvvetli olup olmadığını tespit edemiyoruz).
A – 5 – İkiterimli Rassal Değişkenlerin Olasılık Dağılımları (Bernoulli Dağılımı)
(İkiterimli Dağılım)
Yapılan rassal bir denemenin ikiterimli rassal bir deneme olabilmesi için dört temel
özelliği taşıması gerekir:
a) Yapılan rassal deneme, n tane aynı (identical) deneyden (trial) oluşmalıdır (Rassal
deneme: yazı tura atılması olsun. Burada her bir atış, bir deney sayılmaktadır. Peş peşe 5 kez
yazı-tura atılması (
) ise benzer süreçlerin tekrarlanması anlamına gelmektedir).
b) Her bir deneyde olası iki temel sonuç vardır. Bunlardan biri “Başarı” (Success)
olarak adlandırılırken diğeri “Başarısızlık” (Failure) olarak adlandırılır (yazı-tura atılmasında
sadece iki sonuç söz konusudur).
c) Başarı olasılığı, deneyden deneye değişmemekte ve hep p olmaktadır (Yazı tura
atılması rassal denemesinde ilgilendiğimiz olay, yazı gelme olasılığı olsun. Her bir deney için
yazı gelme olasılığı sabit ve 0.5’e eşittir). Bunun doğal bir sonucu olarak başarısızlık olasılığı
da (tura gelme olasılığı) sabit ve (1–p) olacaktır.
d) Rassal denemede yapılan her bir deney, birbirinden bağımsızdır.
İkiterimli bir rassal denemede ilgi alanımız, n tane benzer deneyde ortaya çıkacak olan
başarı sayısı olsun. Burada başarı sayısı bir rassal değişken olarakX ile temsil edilsin ve
alabileceği değerler de 0,1,…,n ile gösterilsin. Dikkat edilirse X rassal değişkeninin
alabileceği değerler sayılabilir çoklukta ve tamsayı değerler olduğundan X kesikli bir rassal
değişkendir. Bu tip bir rassal değişkenin olasılık dağılımı, İkiterimli Rassal Değişkenin
Olasılık Dağılımı olarak adlandırılmaktadır.
4
Örnek 5: Bir mağazaya giren müşterilerin alış veriş yaparak mağazadan çıkması ile
ilgiliyiz. Mağaza yöneticisi, geçmiş tecrübelerine dayanarak, mağazaya giren müşterilerin %
30’unun alış-veriş yaptığını tespit etmiştir. Cevabını aradığımız soru: mağazaya giren son 3
müşterinin 2’sinin alış-veriş yapma olasılığı nedir?
Cevabı aranan soru, ikiterimli bir rassal değişkenin olasılık dağılımı ile ilgilidir.
X rassal değişkeni: 3 müşterinin alış-veriş yapması
Dikkat edilirse yapılan her bir alış-veriş, birbirinden bağımsızdır. Hiçbiri alışveriş
yapmaya bilir (Bu durumda rassal değişken “0” değerini alır); veya “1” veya “2” veyahut “3”
kişinin tamamı alışveriş yapabilir. Ayrıca, kişilerin alış-veriş yapma olasılığı da deneyden
deneye değişmemektedir.
Müşterilerin alış-veriş yapmasını “başarı” olarak nitelendirip “S” harfi ile temsil edelim.
Benzer şekilde müşterilerin alış-veriş yapmamasını “Başarısızlık” olarak adlandırıp “F” harfi
ile temsil edelim. Bu rassal deneme sonucu oluşacak olası sonuçları, aşağıdaki gibi
bulabiliriz:
Bizim ilgi alanımıza giren 3 olası sonuç bulunmaktadır. Burada bir genelleme
yapılabilir. İster peş peşe ister belirli veya belirsiz aralıklarla gerçekleşsin, mümkün olan n
tane eleman arasından x tane elemanlı alt küme sayısını bulmak isteyelim:
5
Buradaki kombinasyon sayısı, n tane elemanda x tane başarı içeren dizilişlerin sayısıdır.
Bu
dizilişler
ile
ilgili
önemli
bir
nokta
da
herhangi
iki
dizilim
aynı
anda
gerçekleşmeyeceğinden bağdaşmaz olurlar. Örneğimize dönecek olursak, üç eleman (n)
içeren her bir sonuç içerisinde iki (x) başarı içeren alt grupları aramaktayız:
Bunun anlamı, rassal deneme sonucunda ortaya çıkan sonuçlardan 3 tanesi, iki başarı
içermektedir. Yukarıdaki şekilde (S,S,F), (S,F,S) ve (F,S,S) olduğu görülmektedir.
Elbette n tane deneme sonucunda x tane başarı ve
tane de başarısızlık elde
edilecektir. Tek bir deneme sonucu bu şekilde bir olasılığa sahipse, n tane birbirinden
bağımsız deneme yapıldığında sonuçların herhangi bir diziliminin olasılığı, tekil sonuçların
olasılıklarının çarpımına eşittir [bağımsız olayların ortak olasılıkları, tekil olasılıkların
çarpımına eşittir:
].
Şimdi aradığımız sonuçları içeren üç durumun olasılıklarını bulalım. Her bir müşterinin
alış-veriş yapma olasılığı 0.3 olduğuna göre:
Başlangıçta yapmış olduğumuz varsayımlarda yapılan her bir deneyin olasılık
sonuçlarının aynı olduğunu söylemiştik. Bu durumda da bir genelleme yapılabilir ve peş peşe
yapılan her bir deney sonucunda n taneden x tane başarı elde etme olasılığı, aşağıdaki gibi
ifade edilebilir:
Örneğimizde n tane (3) mevcut içerisinden x tane (2) başarı, denklemde yerine yazılırsa,
yukarıda bulduğumuz olasılık sonucu elde edilir:
İkiterimli Olasılık Fonksiyonu
6
Örnek 5 için 3 müşterinin alış-veriş olasılıklarının dağılımı, aşağıdaki gibi olacaktır:
3 müşterinin hiçbirinin alış-veriş yapmama olasılığı % 34.3’tür.
3 müşteriden sadece 1’inin alış-veriş yapma olasılığı % 44.1’dir.
3 müşteriden 2’sinin alış-veriş yapma olasılığı % 18.9’dur.
3 müşterinin de alış-veriş yapma olasılığı % 2.7’dir.
İkiterimli Dağılımın Beklenen Değeri
Örnek 5’te 3 müşteri vardı. Bu üç müşterinin ortalama olarak kaç tanesinin alış-veriş
yapması beklenir?
Şayet bu mağazanın 1000 tane müşterisi varsa, kaç tane müşterinin alış-veriş yapması
beklenir?
7
Mağazaya giren 1000 tane müşterinin 300 tanesinin alış-veriş yapması beklenir.
İkiterimli Dağılımın Varyansı ve Standart Sapması
√
Örnek 5 için hesaplayalım:
√
√
Örnek 6: Bir sigortacı belirli bir iş görüşmesinin başarı ile sonuçlanması olasılığını 0.4
olarak görmektedir. Satış yapılırsa “1” satış yapılmazsa “0” değerini alan X rassal değişkeni
tanımlandığında bu değişken, başarı olasılığı p’nin 0.4 olduğu bir ikiterimli dağılımı gösterir.
Satıcının 5 görüşme yaptığını ve her görüşmede satış yapma olasılığının 0.4 olduğunu
kabul edelim. Bu durumda rassal değişken olan satış sayısının (X) dağılımı,
olan bir binom dağılımıdır.
8
ve
Satıcının 5 görüşme sonucunda beklenen satış sayısı ise, bu ikiterimli dağılımın
ortalamasına (beklenen değerine) eşittir:
Örnek 7: Bir basketbolcu iki serbest atış kullanacaktır. Kariyerinde serbest atışlarda
başarı oranı 0.4’tür.
a) İki serbest atıştan oluşacak olası sonuçları ağaç çizimi ile gösteriniz.
b) Serbest atışlar sonucunda sırasıyla hiç sayı atamama, 1 sayı atma ve 2 sayı atma
olasılıklarını hesaplayınız.
Dikkat edilirse soruda verilenlerden hareketle isabetli basket atma rassal değişkeni (X),
ve
ile binom dağılımı göstermektedir.
9
c) Beklenen değerini ve standart sapmasını hesaplayınız ve yorumlayınız.
Bu basketbolcunun 2 serbest atışta 0.8 isabetli atması beklenir.
√
A – 6 – Poisson Olasılık Dağılımı
Belirli bir zaman aralığında veya belirli bir mekân aralığında bir olayın meydana
gelme sıklığının tahmin edilmesinde kullanılan kesikli bir rassal değişkendir. Örneğin bir saat
içerisinde araba yıkama merkezine gelen araç sayısı, otobanda 10 kilometrelik mesafede
tamire ihtiyaç duyan araç sayısı veya petrol boru hattında 200 kilometrelik mesafede meydana
gelen kaçak sayısı. Şayet bir rassal değişkenin meydana gelme sayısı, aşağıdaki iki özelliği
taşıyorsa, Poisson olasılık dağılımı olarak tanımlanır:
(1) Bir olayın meydana gelme olasılığı, eşit uzunluktaki farklı iki aralıkta da aynıdır.
(2) Her hangi bir aralık içerisinde meydana gelme veya meydana gelmeme, bir başka
aralıkta meydana gelme veya meydana gelmemeden bağımsızdır.
Poisson Olasılık Fonksiyonu
: Belirli bir aralıkta x kez meydana gelme olasılığı
: Belirli bir aralıkta meydana gelme sayısının beklenen değeri (ortalaması)
e: 2.71828
10
Örnek 8: Bir çağrı merkezinin bir saatte aranma sıklığı 48’dir.
a) 5 dakika içerisinde bu çağrı merkezinin 3 defa aranma ihtimali nedir?
60 dakikada ortalama olarak 48 defa aranıyorsa 5 dakikada ortalama olarak 4 defa
aranacaktır. 5 dakikalık zaman dilimi için değerler Poisson olasılık fonksiyonunda yerine
yazılır (
):
Bu çağrı merkezinin 5 dakika içerisinde 3 defa aranma olasılığı % 19,5’tir.
b) 10 dakika içerisinde bu çağrı merkezinin 4 defa aranma olasılığı nedir?
60 dakikada ortalama olarak 48 defa aranıyorsa 10 dakikada ortalama olarak 8 defa
aranacaktır. 10 dakikalık zaman dilimi için değerler Poisson olasılık fonksiyonunda yerine
yazılır (
):
Bu çağrı merkezinin 10 dakika içerisinde 4 defa aranma olasılığı % 5.72’dir.
Örnek 9: Uluslararası Sabiha Gökçen havalimanına rassal ve birbirinden bağımsız
olarak dakikada ortalama 10 yolcu gelmektedir.
a) Bir dakika içerisinde 2 yolcu gelme ihtimali nedir?
Bir dakika içerisinde 2 yolcu gelme ihtimali binde 227’dir.
b) 15 saniye içerisinde hiç yolcu gelmeme ihtimali nedir?
Bir dakikada (60 saniye) ortalama olarak 10 yolcu geliyorsa 15 saniyede ortalama
olarak 2.5 yolcu gelecektir.
Bu havalimanına 15 saniye içerisinde hiç yolcu gelmeme ihtimali % 8.2’dir.
11