target akışölçeri için optimum hedef mesafesinin akış perspektifi

I. EGE ENERJİ SEMPOZYUMU VE SERGİSİ
Pamukkale Üniversitesi Mühendislik Fakültesi
Denizli, Mayıs 2003
TARGET AKIŞÖLÇERİ İÇİN OPTİMUM HEDEF MESAFESİNİN
AKIŞ PERSPEKTİFİ YÖNÜNDEN İNCELENMESİ
1, 2, 3
Ümit N. Temel1, K. Melih GÜLEREN 2, Ali PINARBAŞI 3
Cumhuriyet Üniversitesi, Mühendislik Fakültesi, Makine Mühendisliği Bölümü
ÖZET
Endüstride kullanılmakta olan borularda genellikle türbülanslı akım türü hakim olup, bu esnada oluşan
gelişmiş türbülanslı akışı kalibre etmek için kurulan deney setinde akış ölçerler yaygın olarak
kullanılmaktadır. Akış ölçerlerin hareketli parçalarının olmayışı dolayısıyla verim artırıcı çalışmalar
araştırmacıların büyük ilgi odağı olmuştur. Özellikle, akışkanın fiziksel özelliklerinden dolayı (viskozite,
Reynolds sayısı gibi) özellikle hacimsel akış ölçerlerin (düşük Reynolds sayılarında, düşük hız ve yüksek
viskoziteye sahip) dizaynında veya performans artırımda birtakım problemler araştırmacıların halen
ilgisini çekmektedir. Akış ölçerlerde oluşan salınımların frekansının düşüklüğü veya ani değişimler
göstermesi sebebiyle, burada gözlemlenen akış karakteristiğini, vortex üreten cihazlar ile karşılaştırmak
mümkündür. Bunların karakteristiklerini, performansları ile doğru orantılı olarak Reynolds sayısının
düşüklüğü, verdiği sinyallerin kalitesi arasındaki ilişki olarak söyleyebiliriz.
Bu çalışmada düşük Reynolds sayısında (Re=50), hedef (target) akış ölçeri için sonlu hacimler tekniğine
dayalı nümerik metot yardımıyla, akışın çarptığı bölge ile daralan kesit arasındaki mesafenin, akış
perspektifi yönünden irdelenmesi amaçlanmıştır. 6 farklı hedef (target) geometrisi için, akışın, kararlı,
sıkıştırılamaz ve viskoz akış kabulüne dayalı, Navier-Stokes denkleminin çözümü yapılmıştır. Elde edilen
sonuçlar ışığında, optimum mesafenin analizi, akış alanında oluşan hız konturları ile sürüklenme
katsayılarının sunulmasını içermektedir.
ABSTRACT
The pipes which are used in industry contains generally turbulent flow type and the flow measurement
instruments are used for calibrating this type of flow. Scientists are interested these instruments due to not
having movable parts. Especially, because of physical features of flow, such as viscosity, Reynolds
number, and some problems occured during the design and the increased-performance of volume flow
meters, the scientist are interested still in these theme. It is possible to compare the vortex-creater
instruments and the characteristics of flow, owing to the lowest of frequency of the oscillations occurred
in the flow rates. We can say that these charesteristics are related with the Reynols number which is
proportional to performance.
In this study, it is aimed to investigate the lenght between the stagnation region of the flow and the
converging section at the low Reynolds number (Re=50) by helping of the numerical technique based on
the finite volume method for the target flow meter. The Navier-Stokes equations based on the assumption
of steady, incompressible and viscous are solved for 6 different target flowmeter geometry. The results
are presented as the analysis of optimum lenght which represent velocity contours and drag coefficients.
1
SİMGELER
Re : Reynolds Sayısı
xt : Lüle çıkışından hedefe kadar olan mesafe
yk : Bıçaklar arası mesafe
wt : Hedefin boyutu
ρ : Yoğunluk (kg/m3)
V : Hız (m/s)
A : Yüzey Alanı (m2)
g : Yerçekimi ivmesi (m/s2)
Cd : Sürüklenme Katsayısı
F : Kuvvet (N)
u, v : Hız bileşenleri (m/s)
Cp : Basınç Katsayısı
1.
GİRİŞ
Akış ölçümleri, bazen mühendislik uygulamaları için çok zahmetli ve önemli
uğraşlardan biridir. Özellikle yapılan ölçümlerin mümkün olduğu kadar hassas olması
arzu edilen bir olgu olmakla birlikte, bu gereksinimi tam olarak karşılayacak sistemlerin
dizaynı, tüm akış şartları için büyük bir sıkıntı kaynağı olmuştur. Bu uygulamalardan
biri olan ve temelde uygulanan akışın dinamik kuvvetinin bir hedef adı verilen, disk
üzerine aksettirilmesi ve bu kuvvetin bir strengeç yardımıyla dijital olarak hesaplanması
esasına dayanmaktadır. Hedef akış ölçerinin hareketli parçalarının olmayışı ve geniş bir
alana hitap etmesi sebebiyle (gaz ve sıvı ölçümünde), hem uygulama alanı açısından,
hem de bu konuda çalışan birçok araştırmacı açısından ilgi odağı haline gelmiştir. Fakat
bu ilgi özellikle akış karakteristiğinin türbülanslı akım durumunda yeterli hassasiyeti
verecek şekilde yeteri kadar geliştirilmiştir. (Re>2000) Akışın laminer yani viskoziteye
bağımlı olması durumunda (Re<1000), hedef akış ölçerin hassas kalibrasyonu
gereksinimi duyulmaktadır. Üreticiler tarafından belirtilen aralıktaki akış ölçerin vermiş
olduğu sonuçların hassasiyeti konusunda birtakım sıkıntıların bulunduğu bilinmektedir.
2
Bu sebeple özellikle gaz ölçümü esnasında yaşanan bu sıkıntıların sebebini araştırmak
ve mevcut akış ölçerin hassasiyetini artırmak için bir çok araştırma yapılmış olup,
yapılan bu araştırmaların bir çoğunda kesin bir yargı çıkarılamamıştır. Bunlardan
birkaçı Fromm ve Harlow [1], El wahed ve ark.[2], Davis ve ark. [3], Boucher ve
Mazharoglu [4], Honda ve Yamasaki’ nin [5] yapmış olduğu çalışmalar olarak
belirtilebilir.
Bu çalışma ise, düşük Reynolds sayısındaki akışın hakim olduğu ortamda, hedef akış
ölçerin kalibrasyonunda gözlemlenen belirsizliklerin giderilebilmesi amacıyla, lüle ile
hedef arası mesafenin etkileşimi ile hedef genişliğinin akış ölçerdeki akışın fiziğine olan
yansımalarını incelenmesini içermektedir.
2.
MODEL GEOMETRİSİ ve AĞ YAPISI
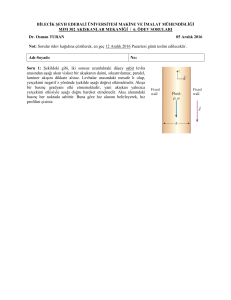
Çalışmada kullanılan hedef akış ölçeri, ince bir hedef ve cidarlar üzerinde bulunan iki
adet keskin bıçak şeklinde engellerden oluşmaktadır (Şekil 1). Boyutsuz olarak ifade
edilen ölçülerde, lüle çıkışından bıçaklara kadar olan mesafe ile bıçaklar arası mesafe
(yk) sabit tutulmuştur. Bunun yanında lüle çıkışından hedefe kadar olan mesafe (xt) için
üç farklı değer alınmıştır (xt: 9,11,13). Benzer durum hedefin boyutu ile ilgilidir.
Hedefin boyutu (wt) için 1.5 ve 2 olmak üzere iki farklı değer kabul edilmiştir. 6 farklı
model için ayrı ayrı analiz yapılmış ve sonuçlar ortaya konmuştur. Analizler tek bir
Reynolds sayısında ve belirli akış kabulleri altında gerçekleştirilmiş olup (Re=50),
optimum mesafenin tespiti için akışın fiziği yönünden irdeleme yapılmıştır.
Geometrisi yukarı ifade edilmiş olan modeller için ayrı ayrı üçgensel elemanlardan
oluşan, Gambit ağ yapıları model ve ağ yaratma programı [6] yardımıyla
oluşturulmuştur. Şekil 2, tek bir model için ( xt:9,yk: 4,wt: 1.5 ) oluşturulan örnek ağ
yapısını içermektedir. Tablo 1. nümerik inceleme amacıyla kullanılan 6 farklı model
için kullanılan eleman ve düğüm sayıları ile geometrik özellikleri gösterilmektedir.
3
Hedef
(Target)
xt
Lüle
girişi
wk
Bıçaklar
yk
Çıkış
Lüle
çıkışı
Şekil 1. Model geometrisi ve boyutsuz ölçüler
Şekil 2. Model geometrisi üzerinde üçgensel ağ yapısı
Model NO
Modeller Özellikleri
Eleman Sayısı
Düğüm Sayısı
1
xt:9,yk: 4,wt: 1.5
18 406
10 045
2
xt:9,yk: 4,wt: 2
18 528
10 112
3
xt:11,yk: 4,wt: 1.5
18 480
10 082
4
xt:11,yk: 4,wt: 2
18 594
10 145
5
xt:13,yk: 4,wt: 1.5
18 698
10 191
6
xt:13,yk: 4,wt: 2
18 858
10 227
Tablo 1. Modeller için geometri ve ağ özellikleri
3.
NÜMERİK ANALİZ METODU VE SINIR ŞARTLARI
Akış, ölçerin lüle tarafından girerek, hedef üzerinde bir kuvvet doğurur. Lüleden geçen
akış, düzlemsel olarak hedef üzerine bir jet uygulayarak iki bıçak arasından hareketine
devam eder. Prensipte lüleden çıkan akışın, hedef üzerinde yaratmış olduğu dinamik
kuvvet, strengeçler yardımıyla görüntülenme esasına dayanır. Uygulanan bu kuvvetin,
akışın türbülanslı olma koşulu ile etkisi;
4
F = CD ρ A
V2
2g
(1)
formülü yardımıyla hesaplanabilir. Fakat akışın Re<2000 olması durumunda,
viskozitenin etkisiyle ortaya çıkan salınımların yarattığı belirsizlik nedeniyle yukarıda
verilen formül işlevini yerine getirmez. Bu sebeple düşük Re sayılarında hassas
kalibrasyon gerekliliği ortaya çıkar ve belirtilen düşük hassasiyeti giderebilmek için
hedef akış ölçerin geometrisi üzerine oluşan etkileşimlerin irdelenmesi gerekmektedir.
Yapılan nümerik analizde akışın kararlı, sıkıştırılamaz ve 2B (2-boyutlu) olduğu kabulü
yapılmıştır. Bu kabuller doğrultusunda Reynolds Sayısının 50 olması durumunda sonlu
hacimler esasına dayalı olarak laminer akış için Navier-Stokes denklemleri çözülmüştür.
Başlangıçta akışkanın sıvı-gaz olması durumunda, kanal içerisindeki hızı hesaplanarak,
bu hız, lüle girişinde ilk sınır şartı olarak uygulanmıştır. Diğer şartlara gelince, çıkışta
debiyi koruyan, dışakış (outflow) [7] sınır şartı ile geriye kalan duvarlar için (hedef
dahil), kaymama (duvar) sınır şartı (u,v=0) verilmiştir.
4.
BULGULAR VE DEĞERLENDİRMELER
Hedef akış ölçerin geometrik boyutlarının, düşük Reynolds sayısında (Re=50) akış
yapısına olan etkilerini incelemek amacıyla, 6 farklı akış ölçer geometrisi üzerinde
nümerik inceleme yapılmıştır. Hedef üzerinde sürüklenme katsayılarının değişimi tüm
geometriler için, belirli iterasyon aralığında olmak üzere Şekil 3’de verilmektedir.
Özellikle hedef genişliğinin küçük seçilmesi (wt=1.5), diğer boyuta nazaran (wt=2)
sürüklenme katsayısında belirgin bir artışla sonuçlanmakta olup, genelde yüksek
salınımlı bir hareket gözlenmektedir. Lüle ile hedef mesafesi arasındaki açıklığın etkisi
irdelendiğinde, xt’nin artışıyla (xt=13), akımın genliğinde belirgin bir azalma
gözlemlendiği gibi, periyodunda da, artış saptanmıştır. xt=9 durumunda yaklaşık olarak
0.06 olan akımın hedef üzerindeki genliğin, xt=13 olmasıyla 0.01 civarında olduğu
Şekil 3.’de verilen Model-1 ile Model-5’in karşılaştırılmasından çıkarılabilir.
Tablo 2.’de ortalama olarak, hedef üzerinde tespit edilen, sürüklenme katsayıları (Cd),
basınç katsayıları (Cp) ile ortalama dinamik basınç değerleri görülmektedir.
5
0,16
0,14
Cd
0,12
0,1
0,08
0,06
0,04
801
851
901
951
1001
1051
1101
1151
1201
1251
1301
İterasyon
MODEL-1
MODEL-2
MODEL-3
MODEL-4
MODEL-5
MODEL-6
Şekil 3. Modeller için hedef üzerinde sürüklenme katsayısının değişimi
Model
NO
1
2
3
4
5
6
Modeller
Özellikleri
xt:9,yk: 4,wt: 1.5
xt:9,yk: 4,wt: 2
xt:11,yk: 4,wt: 1.5
xt:11,yk: 4,wt: 2
xt:13,yk: 4,wt: 1.5
xt:13,yk: 4,wt: 2
Cd
Cp
Ortalama
Dinamik Basınç
0.11 657
0.08 629
0.09 672
0.07 107
0.10 191
0.07 288
16.424
5.909
12.695
6.732
10.812
5.106
1.085
0.451
1.296
0.474
0.629
0.266
Tablo 2. Modeller için hedef üzerinde ortalama sürüklenme katsayısını
Sürüklenme katsayısının, hedef ile lüle mesafesi arasındaki açılığa olan etkisinde
gözlemlendiği gibi, basınç katsayısı ve dinamik basınç değerleri arasında da paralel bir
ilişki göze çarpmaktadır. Bir başka ifadeyle, hedef mesafesi arttıkça belirtilen
değerlerde orantılı bir şekilde azalma olmaktadır.
Şekil 4. altı farklı geometri için ani hız konturlarını içermekte olup, akışın lüle
çıkışından itibaren oluşturduğu jet hareketi tüm modeller üzerinde belirgin bir şekilde
kendini göstermektedir. Sol taraftan, maksimum bir hızla kesite giren akışkan, kesit
daralmasının etkisiyle eksende oluşan jet hareketi ile hedefe etkide bulunmaktadır.
Şekil 4. ve Model-1’de görüldüğü üzere hedef mesafesinin yakın olması sebebiyle,
uygulamış olduğu basıncın maksimum olacağı açıkça görülebilir. Eksenel bir jet akımı
ile gelen akış, hedefe etkide bulunması suretiyle iki bölgeli farklı bir akış yapısına
dönüşmektedir. İkincil jet olarak ifade edilen, hedefin üst ve alt kısmında bulunan ve
6
farklı özelliklerde bulunan ikincil jetlerden üst kısımda olanın jet açısının düşük olması
sebebiyle, bıçaklar üzerinde fazla bir etki bırakmadan hareketine devam etmektedir. Alt
MODEL-1
MODEL-2
MODEL-3
MODEL-4
MODEL-5
MODEL-6
Şekil 4. Modeller için ani hız konturları
kısımda bulunan ve üst akıma nazaran daha yüksek eğim açısına sahip olan jet ise katı
duvar ile bıçak arasında bir örtü gibi hareketinde durgunlaşmaya yönelmektedir. Bu
sebepten dolayı, ters akım hareketi bu bölgede gözlemlenir. Hedef genişliğinin 1.5’dan
2’ye çıkarılmasıyla (Model-2) hedef sonrası gözlemlenen ikincil jetlerdeki akış açıları
7
dönüşüme uğrayarak, ilk modele zıt olacak şekilde, alt kısımdaki jetin akış açısının
düştüğü, buna karşın üst kısımdaki jet açısının arttığı görülmektedir. Yine merkezcil
jetin üst ve altında iki bölgeli vortex hareketleri oluşmaktadır. xt mesafesini artırmaya
devam edecek olursak (xt=11, Model-3), Model-1’e paralel olarak ikincil jet hareketinin
hedefin üst kısmında oluştuğu, fakat açıklığın etkisi neticesinde, Model-1’de akış
hareketine katılmayan alt kısımdaki bölgenin mevcut basıncı yenerek harekete katıldığı,
buna karşın hedefin arka kısmında büyük çaplı bir vortex göbeği meydana geldiği
görülmektedir. Hedef genişliğinin etkisi irdelendiğinde (Model-4), akımın yapısında
belirgin bir değişim gözlemlenmekte olup, merkezcil jetin, hedefin üzerine etkimesiyle
oluşan akış yapısında eksenel simetrik bir yapıya dönüştüğü söylenebilir.Yani hedef
sonrası oluşan çıkış açılarında paralellik, buna karşın hedef öncesi jetin üst ve alt
kısmında düşük basıncın hakim olduğu iki bölgeli vortex merkezi görülmektedir. Hedef
ile lüle mesafesini biraz daha artırdığımızda (xt=13, xt =1.5, model 5) lüleden çıkan
jetin, hedef genişliğinin yeteri büyüklükte olmaması sebebiyle, akışta düzgünsüzlük
göze çarpmaktadır. Özellikle üst kısımdaki ikincil jetin, bıçağında etkisiyle ters akış
hareketine dönüştüğü, sadece alt kısımdaki jetin hareketine devam ettiği söylenebilir.
Model-6’ya gelindiğinde, yani hedef genişliğini 2’ye çıkardığımızda Model-4’e benzer
şekilde simetrik akış hareketi göze çarpar. Her iki bölgesel akışın hedef sonrası
birleşerek çıkışa doğru hareketini tamamladığı görülmektedir.
5- SONUÇLAR
Hedef akış ölçerin altı farklı geometrisi üzerinde nümerik inceleme yapılarak optimum
hedef mesafesinin akış yapısı üzerinde etkisi irdelenmiştir. Hedef genişliği ile
mesafenin etkisi dikkate alındığında optimum mesafenin 11<xt<13 arasında olması
buna karşın wt’nin ise 2 olmasının akışın yapısına pozitif yönde etki ettiği sonucu
çıkarılmıştır. Ortalama sürüklenme ve basınç katsayısı açısından irdelendiğinde ise
benzeri sonuçlar elde edilmiş olup literatürle karşılaştırıldığında benzer yaklaşımlar
olduğu vurgulanmıştır. Gerçekte akış ölçer içerisindeki akışın kararsız olması sebebiyle
ileriki çalışmalarda, akış kabulünü bu doğrultuda kabul edip, çalışmaya devam edilmesi
düşünülmektedir.
8
6- KAYNAKLAR
1.
Fromm JE., Harlow FH., “Numerical solution of the problem of vortex street
development” Phys. Fluids. V:6, pp:975-982, 1963
2.
El Wahed AK., Johnson MW., Sproston JL., “Numerical study of vortex sheeding
from different shaped bluff bodies” Flow Meas. Instrum., v:4, n:4, pp:233-240,
1993
3.
Davis RW., Moore EF., Purtell LP., “A numerical,experimental study of confined
flow around rectangular cylinders” Phys. Fluids. V:27 (1), pp:46-59, 1984
4.
Boucher RF, Mazharoglu C., “Low Reynolds number fluidic flowmetering” J.
Phys. E Sci. 21, 977-989, 1988
5.
Honda S., Yamasaki H., “A new hydrodynamic oscilator type flowmeter” Int.
Symp.On Fluid Control and Measurement, Tokyo, 1985
9