Solenoid_toroid

A.Ozansoy
13.05.2015
Örnek 9.9. Solenoidin (Akım makarası=bobin) Manyetik Alanı:
Bir solenoid, helis biçiminde sarılmış uzun bir teldir. Manyetizmada, düzgün manyetik alan
elde etmek için solenoid kullanılır. Sarımlar yeterince sıkı olduğunda solenoidin iç kısmında
sabit bir alan elde edilir. Sarımlardan her birine çembersel bir akım ilmeği gözüyle bakılabilir
ve toplam manyetik alan tüm sarımlardan gelen katkıların vektörel toplamıdır.
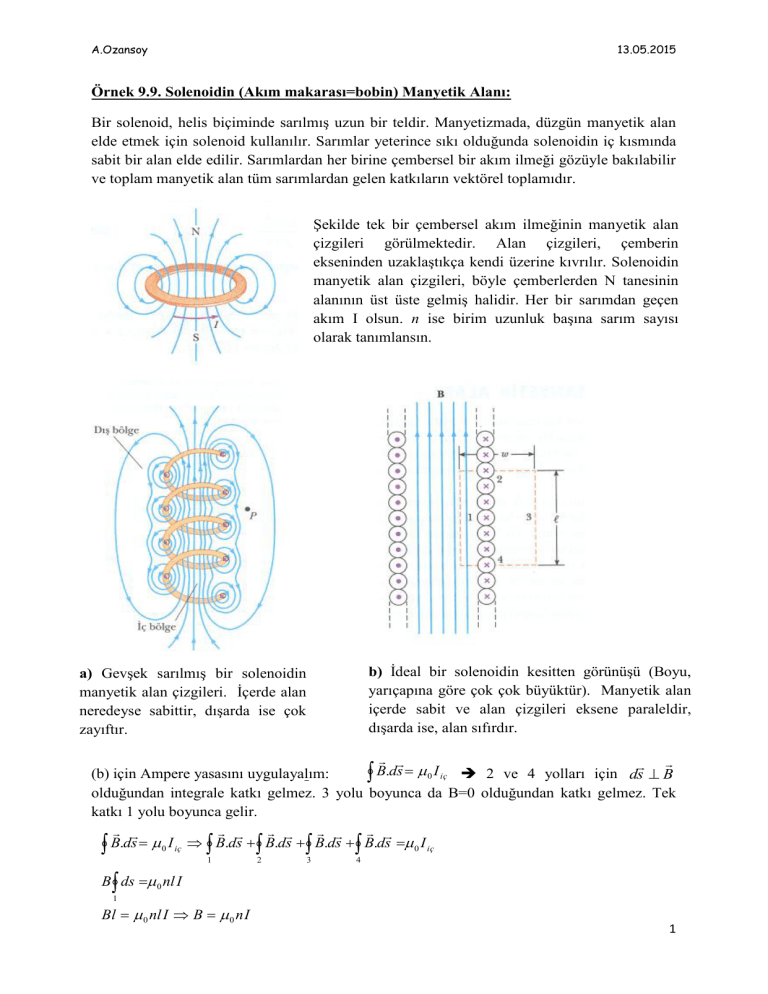
Şekilde tek bir çembersel akım ilmeğinin manyetik alan
çizgileri görülmektedir. Alan çizgileri, çemberin
ekseninden uzaklaştıkça kendi üzerine kıvrılır. Solenoidin
manyetik alan çizgileri, böyle çemberlerden N tanesinin
alanının üst üste gelmiş halidir. Her bir sarımdan geçen
akım I olsun. n ise birim uzunluk başına sarım sayısı
olarak tanımlansın.
b) İdeal bir solenoidin kesitten görünüşü (Boyu,
yarıçapına göre çok çok büyüktür). Manyetik alan
içerde sabit ve alan çizgileri eksene paraleldir,
dışarda ise, alan sıfırdır.
a) Gevşek sarılmış bir solenoidin
manyetik alan çizgileri. İçerde alan
neredeyse sabittir, dışarda ise çok
zayıftır.
 
 
B
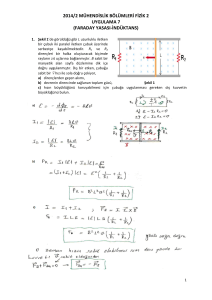
(b) için Ampere yasasını uygulayalım:
 .ds   0 I iç  2 ve 4 yolları için ds  B
olduğundan integrale katkı gelmez. 3 yolu boyunca da B=0 olduğundan katkı gelmez. Tek
katkı 1 yolu boyunca gelir.
 
 
 
 
 
B
.
d
s


I

B
.
d
s

B
.
d
s

B
.
d
s

B
0 iç




 .ds  0 I iç
1
2
3
4
B  ds  0 nl I
1
Bl   0 nl I  B   0 n I
1
A.Ozansoy
13.05.2015
Örnek 9.10. Toroidin Manyetik Alanı:
Bir toroid, iletken olmayan bir maddeden yapılmış, simit biçimli içi boş bir halkanın etrafına
sarılmış N tane iletken sarımdan oluşur. Merkezden r uzaklık için manyetik alanı
hesaplayalım:
Toroid içinde r yarıçaplı bir çember seçelim.
Çember boyunca B, yol elemanı ds’ ye paraleldir.
 
B
 .ds   0 I iç
B  ds  0 N I
B(2r )   0 N I  B 
0 N I
2r
2