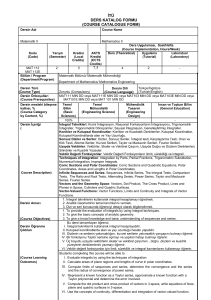
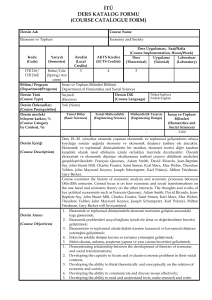
İstanbul Ticaret Üniversitesi Fen Bilimleri Dergisi Yıl:10 Sayı 19 Bahar 2011 s.37-50
ASYMPTOTIC I EQUIVALENT SEQUENCES
Hafize (GÖK) GÜMÜŞ*, Jeff CONNOR**
Geliş: 21.04.2011 Kabul: 07.07.2011
ABSTRACT
Fridy defined asypmtotic equivalence where x ( xk ) and y ( y k ) are real sequences and Pobyvanets
obtained conditions for asypmtotic equivalence for a non-negative summability matrix. Marouf studied
about asypmtotic equivalent sequences. Recently Gok, Nuray and Connor defined asypmtotic Iequivalent sequences where I is an ideal in the set of natural numbers N. The purpose of this paper is
define asymptotic ∆I- equivalence of two non-negative x ( xk ) and y ( y k ) sequences and study
about ∆I- regularity of an A (a nk ) infinite matrix where
x (xk ) ( xk xk 1 ) .
Key Words: Asymptotic equivalence,, Asymptotic I-equivalence, Difference aequences..
ASİMPTOTİK
I DENK DİZİLER
ÖZET
x ( xk ) ve y ( y k ) reel diziler olmak üzere Fridy bu diziler için asimptotik denklik kavramını
tanımlamış ve Pobyvanets negatif terimli olmayan bir toplanabilme matrisi için asimptotik regulerlik
şartlarını elde etmiştir. Daha sonra Marouf asimptotik denk diziler üzerine çalışmıştır. Gok, Nuray ve
Connor, I ideali N doğal sayılar kümesinde bir ideal olmak üzere, asimptotik I-denk dizileri
tanımlamışlardır.
Bu çalışmanın amacı, negatif terimli olmayan x ( xk ) ve y ( y k ) dizilerinin I asimptotik
x (xk ) ( xk xk 1 ) olmak üzere A (ank ) sonsuz matrisinin I
regulerliğini çalışmak olacaktır.
Anahtar Kelimeler: Asimptotik denklik, asimptotik I-denklik, Fark dizileri.
denkliğini tanımlamak ve
* Afyon Kocatepe University, Department of Mathematics, Afyonkarahisar , TURKEY [email protected]
** Ohio University, Department of Mathematics, Athens, Ohio, USA [email protected]
Hafize (GÖK) GÜMÜŞ, Jeff CONNOR
1. INTRODUCTION
Statistical convergence was introduced by Fast in 1951 and after that Kostyrko,
Mačaj and Šalát defined I -convergence for real sequences. Kostyrko, Salát and
Wilezyński applied this concept in an arbitrary metric space. I -convergence is kind
of generalization of statistical convergence and it is based on the concept of ideal.
Definition 1.1. Let x ( xk ) is a real number sequence and |.| is cardinality of any
set A. For each
0 if
lim n
1
k n : xk L 0
n
then x is statistical convergent to L and it is denoted by st lim x L . The
set of all statistical convergent sequences is denoted by S . (Fast, 1951)
Definition 1.2. A family
ideal if
(i)
I 2 N of subsets of N positive integers is said to be an
I
(ii) For each A, B I we have A B I
(iii) For each A I and B A we have B I
An ideal is called non-trivial if
n I
for each
n N . (Kostyrko, Salát and Wilezyński, 2000)
Definition 1.3. A family
filter if
(i)
N I and a non-trivial ideal is called admissible if
F 2 N of subsets of N positive integers is said to be an
F
(ii) For each A, B F we have A B F
(iii) For each A F and B A we have B F
(Kostyrko, Salát and Wilezyński, 2000)
There is an important connection between ideals and filters in that if I is an ideal in
N then F ( I ) N \ A : A I is a filter in N. (Kostyrko, Salát and Wilezyński,
2000)
38
İstanbul Ticaret Üniversitesi Fen Bilimleri Dergisi
Bahar 2011
Definition 1.4. Let x ( xk ) is a real sequence and I 2 N is an admissible ideal.
If for each 0
A( ) k : x k L
belongs to I then x is
I lim x L . The set of all I
of all
I convergent to L and this is written by
convergent sequences is denoted by c I and the set
I convergent sequences to zero is denoted by
c0 ( I ) . (Kostyrko, Salát and
Wilezyński, 2000)
In 1981 Kızmaz defined difference sequences. Let l , c and c 0 are bounded,
convergent and null sequences, respectively. He introduced
l () x ( xk ) : x l
c() x ( xk ) : x c
c0 () x ( xk ) : x c0
sequence spaces where x ( xk ) is a real sequence and x (xk ) ( xk xk 1 ) .
(Kızmaz, 1981)
Let x ( xk ) and y ( yk ) are real sequences. Asymptotic equivalence is defined
for x and y as follows: If
lim n
xk
1
yk
then x and y are called asymptotic equivalent; this is denoted by x ~ y . (Fridy,
1978) Pobyvanets introduced asymptotic regular matrices which preserve the
asymptotic equivalence of two nonnegative number sequences, that is, for the
nonnegative matrix A (a jk ) if x ~ y then Ax ~ Ay . (Pobyvanets, 1980)
Theorem 1.1. Let A (a jk ) is a non-negative matrix. A is asymptotic regular if and
only if for each
m
lim n
a nm
a
k 1
0
nk
(Pobyvanets, 1980)
39
Hafize (GÖK) GÜMÜŞ, Jeff CONNOR
The frequency of terms having zero values makes a term-by-term ratio
xk
yk
inapplicable in many cases, which motivated Fridy to introduced some related
notions. In particular, he analyzed the asymptotic rates of convergence the tails and
partial sums of series and the supremum of the tails of bounded sequences. He used
nm
n m
Rm x x n if x l1 , S m x x n if x l1 and
m x sup nm xn if
x l and he investigated the rates Rm x , S m x ve m x .
Rm y S m y
Define
m y
l1 , P0 , P and P spaces as follows:
l1 x ( x n ) : x n
k 1
P0 {the set of all nonnegativ e sequences which have at most a finite number
of zero terms}
P {the set of all sequences x such that x k 0 for all k}
P {The set of all real number sequences such that x k 0 for all k }
Theorem 1.2. If A is a nonnegative
statements are equivalent:
(l , l1 ) summability matrix, then the following
x and y are bounded sequences such that x ~ y and y P for some δ>0,
then RAx ~ RAy .
(i) If
a km
(ii) For each m , lim n k n
a kj
k n j 0
0
(Marouf, 1993)
In 2003, Patterson extended these concepts by introducing asymptotically statistical
equivalent sequences, an analog of the above definitions, and investigated natural
regularity conditions for nonnegative summability matrices. Patterson and Savaş,
40
İstanbul Ticaret Üniversitesi Fen Bilimleri Dergisi
Bahar 2011
defined asymptotic lacunary statistical equivalent sequences by using lacunary
sequences. (Patterson and Savaş, 2006)
Definition 1.5. Two nonnegative sequences x and
statistical equivalent provided that for every 0
y are said to be asymptotically
x
lim n k n : k 1 0
yk
S
In this case we write
x ~ y . (Patterson, 2003)
Asymptotically statistical reguler matrices can be defined similar to aymptotic
reguler matrices.
Definition 1.6 A summability matrix
S
S
provided that Ax ~ Ay whenever x ~ y ,
(Patterson, 2003)
A is asymptotically statistical regular
x P0 and y P for some 0.
Having introduced these ideas, Patterson then offered characterizations of (i) in
theorem 1.2. when a nonnegative summability matrix A that maps bounded
sequences into the absolutely convergent sequence and has the property that if
S
S
x P0 and y P and x ~ y , then RAx ~ RAy and (ii) when a summability
matrix is asymptotically statistical regular summability matrices.
Theorem 1.3. In order for a summability matrix A to be asymptotically statistical
regular it is necessary and sufficient that:
k0
(i)
ka
nk
is bounded for each n.
k
(ii) For any fixed
k 0 and 0
lim n
1
the number of k n :
n
k0
a
nk
a
nk
k n
k 1
0
41
Hafize (GÖK) GÜMÜŞ, Jeff CONNOR
(Patterson, 2003)
2. MAIN RESULTS
Definition 2.1. Let
x (xk ) ( xk xk 1 ) ve y (y k ) ( y k y k 1 )
are non negative real sequences.
If
lim n
then
xk
1
yk
x and y sequences are called -asymptotic equivalent sequences and this is
denoted by x ~ y .
x ( xk ) and y ( y k ) are nonnegative real sequences and I
is an admissible ideal in N. If for every 0
Definition 2.2. Let
xk
1 I
k N :
yk
then x and y sequences are called I -asymptotic equivalent sequences and this is
I
denoted by x ~ y .
Definition 2.3. Let x and
y are nonnegative real sequences and ve I is an
admissible ideal in N. If for every 0
xk
1 I
k N :
yk
then
x and y sequences are called I -asymptotic equivalent sequences and this
I
is denoted by x ~ y .
Proposition 2.1. If
x and y sequences are asymptotic
also asymptotic I equivalent i.e. if
I equivalent then they are
I
x ~ y then x ~ y .
Proof: If we consider I I f A N : A is finite then we have the proof.
42
İstanbul Ticaret Üniversitesi Fen Bilimleri Dergisi
Bahar 2011
I
Following example shows that for real sequences x and
y when x ~ y then it
I
doesn’t need to be
x~ y.
xk 1 1
Example 2.1. Choose
I lim k
xk
1 but I lim k
yk
and
k
xk
1 .
yk
yk 1 1
Theorem 2.1. Let A (a jk ) is a non negative
k
sequences. Then
(l , l1 ) summability matrix and
I, J are admissible ideals in N. Then the following statements are equivalent:
(i)
If
x
y
and
I
are
bounded
sequences
such
that
x~ y,
x P0 and y P for some 0 then R Ax ~ R Ay .
J
(ii) J lim n
a
jk
a
jk
j n k S
j n k 1
0 for all S I .
Proof: The proof that statement (ii) implies statement (i) is given first. Assume that
I
x ~ y , 0 and the set S is defined such that
x k
S k :
1
2
y k
Observe that
S I and that
1 y k xk 1 y k
2
2
for each k S . By (ii) ,
43
Hafize (GÖK) GÜMÜŞ, Jeff CONNOR
T n N :
a
j n kS
jk
a
j n k 1
jk
F (J )
2 sup k x k
For n T ,
a
j n kS
jk
a
j n k 1
2 supk xk
jk
therefore
a jk xk
Rn Ax j n k 1
Rn Ay
a jk yk
j n k 1
xk a jk xk
j n kS
kS
a jk yk
j n k 1
a
jk
supk xk a jk 1 a jk yk
2 kS
j n kS
a jk yk
j n k 1
sup k x k
a
j n kS
a
j n k 1
1
2
jk
sup k x k
1
2 sup k x k 2
1
44
jk
İstanbul Ticaret Üniversitesi Fen Bilimleri Dergisi
Bahar 2011
i.e.
Rn Ax
1
Rn Ay
(2.1)
On the other hand,
a jk xk
Rn Ax j n k 1
Rn Ay
a jk yk
j n k 1
sup k y k
a
j n kS
sup k y k
a
j n k 1
jk
j n kS
a jk
a
j n k 1
sup k y k
j n kS
a
j n k 1
jk
y k
1 a jk y k
2 j n k 1
j n k 1
a jk
xk a jk xk
j n kS
kS
a jk yk
j n k 1
jk
1 a jk y k
2 j n kS
jk
a jk
a
a jk y k
1 a jk y k
2 j n kS
a
j n k 1
1
2
jk
By condition (ii) there is a set
j n k 1
jk
1
sup
y
k
k a jk
2
j n kS
a jk
j n k 1
U F (J ) such that, for each n U , the first and
third terms of the above expression can be made small in relation to
particular ,
y k
Rn Ax
1
Rn Ay
1
2
and, in
(2.2.)
45
Hafize (GÖK) GÜMÜŞ, Jeff CONNOR
for each n U . By (2.1) and (2.2) we have
Rn Ax
1
Rn Ay
J lim
and hence (ii) implies (i).
The proof is completed by showing that statement (i) implies statement (ii). Assume
I
that
x and y are bounded sequences, x P0 , y P and x ~ y , then
R Ax ~ R Ay . Let S is a member of I and define the sequences x and
y as follows:
J
1, k S ise
xk
0, k S ise
and
Observe that
x k a jk x k
k S
k S
a jk y k
j n k 1
a
Ax
Rn
R n Ay
jn
jk
a
j n k 1
jk
a jk
j n k S
a
j n k 1
1
jk
a
j n k S
jk
a
j n k 1
jk
and, as R Ax ~ R Ay . it follows that
J
J lim
a
j n k S
0.
a
j n k 1
46
jk
jk
yk 1
İstanbul Ticaret Üniversitesi Fen Bilimleri Dergisi
Lemma 2.1. Let
Bahar 2011
x and y belong to P l and I is an admissible ideal in
I
N. Then necessary and sufficient condition for x ~ y is I lim k ( xk yk ) 0 .
I
Proof: Assume that x ~ y then
x
T k : k 1 F ( I )
yk
and for each k T we have
1 y k
x k 1 y k
and hence
1 yk xk 1 yk yk xk yk yk
supk yk xk yk supk yk
' xk yk '
(For each k T )
And hence I lim k xk yk 0 .
Now suppose that I lim k xk yk 0 then
B k : xk yk F ( I )
For each
k B we have
xk yk
xk
1
yk yk
yk
1
xk
1
yk
xk
1
yk
47
Hafize (GÖK) GÜMÜŞ, Jeff CONNOR
x
k : k 1 F ( I )
yk
I
and hence x ~ y .
Definition 2.4. Let I be an admissible ideal in N, x is a real sequence and
A (a jk ) is a nonnegative summability matrix. If I lim x L implies
I lim Ax L then A is called an I-regular matrix. (Gok Gumus, 2011)
Theorem 2.2. Let A (a jk ) is a nonnegative summability matrix,
I is an admissible ideal. The matrix
(i)
j:
a
kS
jk
A (l , l1 ) and
A is I-regular if and only if
I for all S I .
(ii)
I lim a jk 1
k 1
(Gok Gumus, 2011)
Definition 2.5. Let A (a jk ) is a nonnegative summability matrix and let
I is an
admissible ideal in N. x and y are nonnegative real sequences with x P and
y P for some δ>0. The summability matrix A is said to be asymptotic
I regular if x ~ y implies Ax ~ Ay .
I
I
Theorem 2.3. Let I 2 N is an admissible ideal in N. Then a nonnegative
summability matrix
A (a jk ) is asymptotic I regular if and only if
a
jk
a
jk
I lim k S
k 1
0
for every S I .
Proof: Assume that A is a asymptotic I - reguler matrix. Let
the sequences x and y as follows:
48
S I and choose
İstanbul Ticaret Üniversitesi Fen Bilimleri Dergisi
1, k S ise
xk
0, k S ise
Bahar 2011
yk 1
and
Observe that x and y are bounded sequences , x P0 and y P . Hence
Ax j
Ay j
a jk xk a jk xk
kS
kS
a
k 1
jk
a a
k 1
yk
jk
kS
a
k 1
Since Ax ~ Ay it follows that
jk
a
jk
a
jk
1 kS
jk
k 1
I
I lim
a
jk
a
jk
kS
k 1
0
Now define the matrix D (d jk ) by d a jk
jk
a
k 1
(2.3)
. Note that, since the row sums
jk
equal 1 and condition (2.3.) yields criteria (i) of Theorem 2.2. B is an I-regular
matrix. Also observe that, since the row sums equal 1, the matrix B maps members
of P to P . Observe that
x ~ y I - lim x y 0
I
I lim Dx y 0
I lim Dx Dy 0
Dx ~ Dy
I
And hence
49
Hafize (GÖK) GÜMÜŞ, Jeff CONNOR
Dx j
Dy j
d
jk
xk
d
jk
yk
k 1
k 1
k 1
k 1
a jk
xk
a
k 1
jk
a jk
a
k 1
yk
a
jk
xk
a
jk
yk
k 1
k 1
jk
Since Dx ~ Dy it follows that Ax ~ Ay .
I
I
REFERENCES
Fast, H., (1951), "Sur la convergence statistique", Coll. Math. 2, 241-244.
Fridy, J.A., (1978), “Minimal Rates of summability”, Can. J. Math., Vol. XXX, 4,
808-816.
(Gok) Gumus, H., Nuray, F. and Connor, J., “Asymptotic I-Equivalence”, submitted
(Gok) Gumus, (2011), “Fark Dizilerinin I-Yakınsaklığı ve Asimptotik I-Denkliği”,
Doktora Tezi, Afyon Kocatepe Üniversitesi, Fen Bilimleri Enstitüsü
Kızmaz, H., (1981), "On certain sequence spaces", Canad. Math. Bull. 24, no. 2,
169-176.
Kostyrko, P., Maćaj, M. and Šalát , T., "Statistical convergence and I-convergence",
Real Analysis Exch.,
Kostyrko, P., Šalát , T. and Wilezyński, W., (2000), "I-convergence", Real Anal.
Exchange 26, no. 2, 669-685.
Marouf, M. S., (1993), Asymptotic Equivalence And Summability. Internat. J. Math
& Math. Sci. Vol. 16 No.4, 755-162.
Patterson, R.F., (2003), “On Asymptotically Statistical Equivalent Sequences”,
Demonstratio Mathematica Vol. XXXVI, No 1.
Patterson, R.F, Savaş, E., (2006), “On Asymptotically Lacunary Statistical
Equivalent Sequences ”, Thai Journal of Mathematics, Volume 4, Number 2, 267272.
Pobyvanets, I.P., (1980), “Asymptotic Equivalence of some Linear Transformation
Defined by a Nonnegative Matrix and Reduced to Generalized Equivalence in the
sense of Cesáro and Abel”, Mat. Fig. 28, 83-87.
50