Test 1`in Çözümleri Basit Makineler

9
Basit Makineler
3. Verilen düzenekte yük 3
ipe bindiği için kuvvetten
kazanç 3 tür. Bu nedenle
yoldan kayıp da 3 olacaktır.
Test 1’in Çözümleri
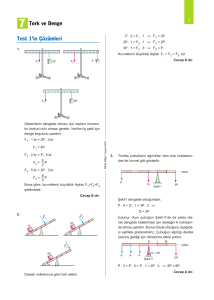
1.
2P
1
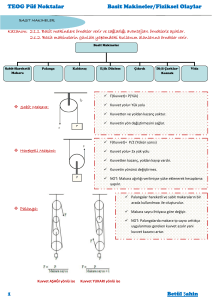
BASİT MAKİNELER
kasnak
Yükün 15x kadar yükselmesi için kasnağa bağlı
ipin 15x . 3 = 45x çekilmesi gerekir. Kasnağın çevresi 3x olduğundan;
45 x
Devir sayısı =
= 15
3x
bulunur.
3P
3P
P
2P
3P
yük
Cevap C dir.
Şekil üzerindeki bilgilere göre dinamometre 2P
değerini gösterir.
2. Dişli ve kasnaklarda devir sayısı yarıçapla ters
orantılıdır. Bir başka ifadeyle büyük tekerler az,
küçük tekerler çok döner.
Nihat Bilgin Yayıncılık©
Cevap D dir.
4.
F3
3
4
F2
F1
F4
P
K
2r
1
4
1
2
P
I
Z
T
Y
X
r
3r
L nin
1
tur dönmüş hâli
4
Dişlilerin devir sayısı n olmak üzere;
3.
2r = nB .3r
4
1.
r = nL .2r
2
P
L
B
A
P
& nB = 1 = nA
2
& nL = 1
4
1
bulunur. Buna göre L dişli çarkı ok yönünde
4
devir yapar ve şekildeki gibi görünür.
Cevap D dir.
II
III
IV
Makara ve palanga sistemlerinde kuvvetten kazanç
sayısı kadar yoldan kayıp vardır. Kuvvet kazancı
yükün bindiği ip sayısı kadardır.
P
F1 =
2
P
F2 =
2
P
F3 =
4
F4 = P
olduğundan F1 ve F2 kuvvetlerinin büyüklüğü eşittir.
Cevap A dır.
2
BASİT MAKİNELER
5.
7.
F1
K
L
2r
F2
r
O2
O1
P
P
Dişli çarklarda, devir sayısı ile yarıçap ters orantılıdır. Ayrıca birbirine dokunan iki dişli çark zıt yönlerde döner.
5
L dişlisi saat ibresi tersine
tur dönerse, K dişlisi
4
5
saat ibresi yönünde
tur döner.
8
3r
r
F3
F4
P
P
Cevap C dir.
F5
P
h
3h
Nihat Bilgin Yayıncılık©
Tüm sistemlere denge koşulunu uygulayalım;
2
F1 . 5 = P . 2 & F1 = P
5
1
4 F2 = P & F2 = P
4
1
3 F3 = P & F3 = P
3
1
F4 . 3 r = P . r & F4 = P
3
1
F5 . 3 h = P . h & F5 = P
3
olur. P yükünü dengeleyen kuvvetler yazıldığında
en küçük kuvvetin B seçeneğinde olduğu görülür.
Cevap B dir.
6.
P
D1
P
8. Eşit bölmeli XY çubuğu Şekil I deki gibi dengede
kaldığına göre, çubuk türdeş değildir. İpteki gerilme kuvveti çubuğun ağırlığına eşittir.
P
T2=3P
D2
P
2h
P
P
D3
h
P
T1=P
P
P
P
Verilen şekillerde P ağırlığındaki cisimler serbest
bırakıldığında D1 ve D2 dinamometrelerine bir yük
binmez.
Cevap D dir.
T1
T2
=
1
bulunur.
3
Cevap C dir.
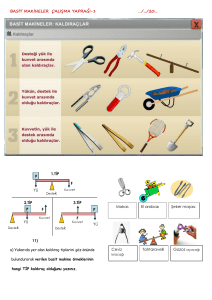
9. Elle taşınamayacak bir cismi maşayla taşırken
yaklaşık olarak orta noktasına F kuvvetini uygularız.
destek
noktası
11. F = 10 N
3 ip
T = 30 N
yük
a
X
a
yük ( P )
kuvvet ( F )
orantısı ile bulunur. Sistem dengede olduğuna
göre destek noktasına göre moment alınır.
Kuvvet kazancı, yani mekanik avantaj
destek
G
Şekil I de XY çubuğu dengede olduğuna göre,
çubuğun ağırlık merkezi desteğin olduğu noktadır.
Palangada 3 tane paralel ip olduğundan kuvvet
kazancı 3 tür. Bu nedenle ipteki T gerilme kuvveti
30 N olur. Desteğin olduğu noktaya göre moment
alırsak;
F . a = P . 2a
P
1
=
F
2
yazabiliriz. Buna göre; kuvvetten kazanç sağlanmamıştır. Basit makinelerde ya kuvvetten kazanılır ya da yoldan kazanılır. Eğer kuvvetten kazanılmışsa kuvvetten kazanç miktarı kadar yoldan
kayıp vardır. Eğer kuvvet kaybı varsa bu kez de
aynı oranda yoldan kazanç vardır.
3
BASİT MAKİNELER
T . 4= G . 2
30 . 4= G . 2 ⇒ G = 60 N bulunur.
Cevap E dir.
Nihat Bilgin Yayıncılık©
Cevap E dir.
12. D1 dinamometresi P ağırlığını
gösterir.
2
P
3
D2 dinamometresi P ağırlığı1
nın
ünü gösterir.
3
2P
D 3 dinamometresi de
3
ağırlığını gösterir.
P
3
P
3
F= P
3
Cevap E dir.
P
P
10.
13. Aynı ipteki gerilme kuvveti
her yerde aynıdır. P yükünün bindiği ipteki gerilme
kuvveti de P kadar olur.
Bunu takip ettiğimizde;
L
K
m
2P
2P
X = P + 2P + P = 4P
Arif
P
bulunur.
L makarası sabit makara olup, tavana bağlıdır. Bu
makaranın ağırlığı ipe binmediğinden Arif’in uyguladığı kuvvete bir katkısı yoktur.
Cevap C dir.
P
P
P
X
Cevap B dir.
4
BASİT MAKİNELER
14.
16.
P1
4
K
F
20 N
F
F F
3F
P1
L
30 N
P2
KL çubuğu dengede olduğuna göre;
P1
· 3 = P2 . cos a . 2
4
P1
8
= cos a bulunur.
P2
3
Bir cismin ağırlığı dünyanın merkezine doğru gösterilir. Şekilde 20 N luk ağırlığın ip doğrultusunda
bir bileşeni yoktur. Bu nedenle 20 N ağırlığındaki
bu cismin ağırlığı dikkate alınmaz.
Cevap A dır.
3F = 30
F = 10 N bulunur.
Nihat Bilgin Yayıncılık©
Cevap E dir.
15.
T=2P
Fk
17.
X
Z
4P
sv
X
P
Y
Sıvı içinde dengede olan X cisminin hacmi 3V
olsun. Buna göre;
Fk + 2P = 4P
Fk = 2P
2V.dsıvı . g = 2P
3V . dX . g = 4P
dX
d sıvı
=
⇒
4
bulunur.
3
Cevap B dir.
Birbirine dokunmakta olan iki dişli çarktan biri saat
ibresi yönünde dönerse, öteki dişli çark saat ibresinin tersine yönde döner.
Şekildeki X dişlisinin saat ibresi yönünde döndüğünü varsayalım. Bu durumda öteki dişlilerin dönme
yönleri şekildeki gibidir. Buna göre, Y dişlisi ile P
dişlisi aynı yönde döner.
Cevap C dir.
5
BASİT MAKİNELER
3.
Test 2’nin Çözümleri
P1 = P alarak iplerdeki gerilme kuvvetlerini aşağıdaki şekil üzerinde gösterelim.
1.
yatay
P
2
P
2
balk oltas
makas
P
2
el arabas
P
P
P3 = 2
P
Cambız, maşa, olta, insan kolu gibi basit makinelerde yük bir uçta, destek öteki uçtadır. Bu tür kaldıraçlarda kuvvetten kayıp, yoldan kazanç sağlanır.
P1 = P
P2 = 2P
Makaslarda destek ortada olduğundan kuvvet kolu
ile yük kolunun uzunluğuna göre kuvvetten kazanç
sağlanmayabilir.
Şekil üzerindeki bilgilere göre, P2 > P1 > P3 olur.
Cevap A dır.
El arabalarında destek bir uçta, yük ise ortadır.
Kuvvet kolu her zaman yük kolundan daha uzun
olduğundan kuvvetten kazanç vardır.
Cevap C dir.
Nihat Bilgin Yayıncılık©
4.
x1
Şekil I
m
m
x2
r
O
Şekil II
2r
x3
m
Şekil III
2.
Şekil I sabit makaralarla
kurulu olup kuvvet
kazancı yoktur. Bu
nedenle F1 = P dir.
Şekil II de ise,
P
F2 =
olur.
4
F1
P
=
=4
F2
P
4
m
P
4
P
2
P
4
Şekil I deki sistemde yayın iki ucunda m kütleli cisimler varken denge sağlanmıştır. m kütleli cisimlerden biri duvar vazifesi yaparken, öteki yayın açılmasını sağlar. Bu nedenle x1 açılma
miktarı mg ile orantılıdır.
Şekil II deki sistemde O noktasına göre tork alınırsa yayı açan kuvvetin 2mg olduğu görülür.
Şekil III teki sistemde hareketli makara göz önüne
m
· g olduğu görüalındığında yayı açan kuvvetin
2
lür. Buna göre x2 > x1 > x3 tür.
P
F2 = 4
P
2
P
Cevap D dir.
Cevap E dir.
6
5.
BASİT MAKİNELER
Şekil I deki çubuğun ağırlık merkezi Y noktası olup
ağırlığı P dir. Şekil II deki çubuğun ağırlığı 2P ve
ağırlık merkezi L noktasıdır.
X
Y
Z
K
7.
3r
O2
L
P
r
F
2P
P ile 2P nin bileşkesinin uygulama noktası K noktasıdır.
Cevap D dir.
yer
O1
P ağırlığındaki düzgün ve türdeş çubuğun ağırlığının yarısı, bağlı bulunduğu ipe biner. O2 noktasına
göre tork alırsak;
P
·r
2
F
1
=
bulunur .
P
6
F·3r =
Nihat Bilgin Yayıncılık©
Cevap E dir.
8.
6.
X = P dir. Ayrıca makaranın ağırlığı P olduğundan
asılı olduğu ipteki gerilme kuvveti 3P olur.
T·sin30°
P
P
O
P
P
2P
P
3P
2
O noktasına göre tork alınırsa;
3
T·sin30°·6 = P · 4 + 3 P · 8
2
3T = 30P
T = 10P bulunur.
3P
4P
K
yatay
X
Şekildeki verilere göre çubuğun ağırlık merkezi X
noktasıdır.
Cevap A dır.
Cevap C dir.
7
BASİT MAKİNELER
9.
11.
v
10 N
T1
r r
P
P
Y
37°
T2
X
53°
10 N
F
6P
Pçubuk= 4P
37°
37°
yatay
37°
Cisimlerin ip doğrultusundaki bileşenlerinin toplamı adamın uyguladığı kuvveti verir.
F = 10·sin37° + 10·sin53°
Önce Şekil I deki F kuvvetini P cinsinden bulalım.
F = 6 + 8 = 14 N bulunur.
F . 2r = 6P . r ⇒ F = 3P
bulunur. Şekil I de çubuğun ağırlık merkezi F kuvvetinden d kadar uzakta olsun. Buna göre;
X
Cevap B dir.
Şekil I
Şekil II
Y
F . d = P . (4 – d)
Nihat Bilgin Yayıncılık©
3P . d = P . (4 – d) ⇒ d = 1 birim
bulunur. Buna göre, çubuğun ağırlık merkezi X
noktasından 1 birim ileridedir.
Şekil II de ağırlık merkezine göre tork alınırsa;
T1 . 1 = T2 . 5 ⇒
T1
T2
= 5 bulunur.
Cevap E dir.
12.
0,8T
T
T
B
T
53°
0,6T
10. Sistem dengede olduğuna göre;
3F = GK
GK
F=
3
16 P = G K + F
GK
16 P = G K +
3
G K = 12 P bulunur .
A
37°
F
F
F
K
70 N
16P
F
Sistem dengede olduğuna göre, A noktasına göre,
tork alınırsa;
,
70· · cos 37° + 0,6 T · , · sin 37° = 0,8 T · , · cos 37°
2
3
3
4
4
4
35· + T · = T ·
5
5
5
5
5
140
9T
16 T
+
=
5
25
25
T = 100 N bulunur .
2T = PK + Pmakara
GK
Cevap D dir.
2T = PK + PK
200 = 2PK ⇒ PK = 100 N bulunur.
Cevap B dir.
8
BASİT MAKİNELER
13.
15.
F
T
r
r
F
T
F
r
12 cm
h2
2r
37°
8 cm
d
h1
G.sin 37°
x
P
37°
K
2x
X
G.cos 37°
K
G
h1 = 12 . sin37° = 7,2 cm
h2 = 8 . cos37° = 6,4 cm
Makara dengede olduğuna göre;
P
2F = P & F =
2
P
F · r = T ·2 r & T =
4
bulunur. K noktasına göre tork alınırsa;
T . (h1 + h2) + G . sin37° . 4 = G . cos37° . 6
P
12
24
·13, 6 +
G=
G
5
5
4
17
G=
P bulunur .
12
Cevap A dır.
d
a = ––
3
G=15 N
Sistem dengede olduğuna göre;
T · 2r = x · r
x = 2T
dir. K noktasına göre tork alınırsa;
2d
T·d = G·
3
2
T = 15 · = 10 N
3
x = 2 T = 20 N bulunur .
Nihat Bilgin Yayıncılık©
2a
2d
––
3
Cevap D dir.
16.
r
T3
2r
T1
T2
T2
T1
T3 T3
P
2P
2T3
P
––
2
Y
X
Z
14.
2θ
K
GX
L
GY
M
GZ
6P 6P
12P
T1 · 4·cosi = GX · 2·cosi
GX = 2T1 = 2P
T2 · 3·cos2i = GY · 2·cos2i
GY = 3P
T
12P
Sistem dengede olduğuna göre;
P
T1 = P , T2 = 2P , T3 =
2
dir. K, L ve M noktalarına göre tork alınırsa;
10P
37°
X
24P
Şekildeki sistem dengede olduğuna göre,
T = 10P·sin 37° = 6P
dir. Şekil üzerindeki bilgilere göre X cisminin ağırlığı 24P olur.
i
i
2T3 · 4·cos ( ) = GZ · 2·cos ( )
2
2
GZ = 2P
GY > GX = GZ bulunur.
Cevap A dır.
Cevap C dir.