τ ϕ λ - Kastamonu Eğitim Dergisi

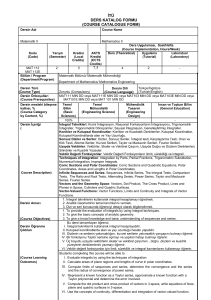
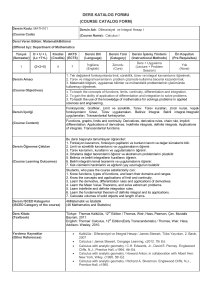
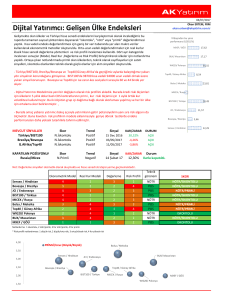
Ocak 2010 Cilt:18 No:1 Kastamonu Eğitim Dergisi 89-98


Arzu AYKUT
Atatürk Üniversitesi, Fen Fakültesi, Matematik Bölümü, Erzurum.

In this paper, we applied two approximate methods for the solution of a boundary value
problem for a differential equation with retarded argument:
x "(t ) + a (t ) x(t − τ (t )) = f (t )
x(t ) = ϕ (t ) (λ0 ≤ t ≤ 0) x(T ) = xτ ,
where
a(t ), f (t ),τ (t ) ≥ 0 (0 ≤ t ≤ T ) and ϕ (t ) (λ0 ≤ t ≤ 0) are
known
as
continuous functions.
Key world: ordinary differential equations, boundry value problem, succesive approximations
method.



Bu çalımada
x "(t ) + a(t ) x(t − τ (t )) = f (t )
x(t ) = ϕ (t ) (λ0 ≤ t ≤ 0) x(T ) = xτ ,
Yava deikenli denklem için konulmu sınır deer probleminin çözümü için iki yaklaık
a(t ), f (t ),τ (t ) ≥ 0 (0 ≤ t ≤ T )
ve
metot
verilmitir.
Burada
ϕ (t ) (λ0 ≤ t ≤ 0) önceden verilmi sürekli fonksiyonlardır.
Key world: ordinary differential equations, boundry value problem, succesive approximations
method
January 2010 Vol:18 No:1 Kastamonu Education Journal
Arzu AYKUT ...
90

A common method used for the analytical solution of the boundary value problems
is the integral equation method [1,2]. With this method, we obtain an integral equation
that is equivalent to the boundary value problem and the solution of the integral
equation is defined as the solution of the boundary value problem. The equivalent
integral equation is usually a Fredholm equation in the classical theory. In this study we
obtain a Fredholm-Volterra integral equation different from classical theory for the
problem
x "(t ) + a(t ) x(t − τ (t )) = f (t )
(1)
x(t ) = ϕ (t ) (λ0 ≤ t ≤ 0), x(T ) = xτ ,
and
a(t ), f (t ),τ (t ) ≥ 0 (0 ≤ t ≤ T ) and
0≤t ≤T
ϕ (t ) (λ0 ≤ t ≤ 0) are known as continuous functions. The Fredholm operator
where
included in the equivalent integral equation is an operator with a degenerated kernel.
We applied the modified successive method and consecutive substitution method for
problem (1). One of these methods suggested by Ja. D. Mamedov [3] has been problem
(1) by Aykut and Yıldız [4].
In this study these methods were applied to the boundary value problem with
retarted argument. We investigated the solution for arbitrary continuous function
τ (t ) .

λ (t ) = t − τ (t ) then t 0 ∈ [0, t ] is a point located at the
left side of T such that conditions λ (t 0 ) = 0 and λ (t ) ≤ 0 ( 0 ≤ t ≤ t 0 ) are
satisfied, where, λ 0 = min 0 ≤t ≤t λ (t ) . We assume that λ (t ) is a nondecreasing
function in the interval [t 0 , t ] and the equation λ (t ) = σ has differential continuous
∗
solution t = γ (σ ) for arbitrary σ ∈ [ 0, λ (t )] . It can be seen that if x (t ) is a
∗
solution of the boundary value for problem (1) then x (t ) is also the solution of the
In problem (1), if we take
0
equation
t
x(t ) = hˆ(t ) +
T

T
0
t
(T − s)a( s ) x(s − τ ( s))ds −  (t − s )a(s ) x( s − τ (s ))ds. (2)
0
Here,
t t
hˆ(t ) = ϕ (0) − ( xT − ϕ (0)) −
T T

T
0
Ocak 2010 Cilt:18 No:1 Kastamonu Eğitim Dergisi
t
(T − s ) f ( s )ds +  (t − s ) f ( s )ds.
0
The Two Method on Equatıon Wıth Retarded Argument ...
Let
91
σ = s − τ (s). Therefore Eq. (2) can be written as follows:
x (t ) = h(t ) +
−
λ (t )
0
t
T

λ (T )
0
(T − γ (σ )a(γ (σ )) x(σ )γ ′(σ )dσ
(3)
(t − γ (σ )a(γ (σ )) x(σ )γ ′(σ )dσ ,
where
t
h(t ) = hˆ(t ) +
T
0
λ (T − γ (σ )a(γ (σ ))ϕ (σ )γ ′(σ )dσ
0
0
(4)
−  (t − γ (σ )a (γ (σ ))ϕ (σ )γ ′(σ )dσ ,
λ0
K 1 (σ ) = [T − γ (σ )]a(γ (σ ))γ ′(σ )
K (t , σ ) = [t − γ (σ )]a (γ (σ ))γ ′(σ ). Therefore we write
Let
x (t ) = h (t ) +
t
T

λ (T )
0
and
K1 (σ ) x(σ ) d σ − 
λ (t )
0
K (t , σ ) x(σ ) dσ
(5)
or
x (t ) + h (t ) +
t
Fλ x + Vλ x
T
(6)
where
Fλ x ≡ 
λ (T )
0
K 1 (σ )x(σ )dσ
is the Fredholm operator,
Vλ x ≡ − 
λ (t )
0
K (t , σ )x(σ )dσ
is the Volterra operator. Eq. (6) is a Fredholm-Volterra integral equation and it is
equivalent to problem (1)

Now, we will define the modified successive approximations for the integral
equation (5), which are different from the ordinary successive approximations, as
follows:
January 2010 Vol:18 No:1 Kastamonu Education Journal
Arzu AYKUT ...
92
x n (t ) = h(t ) +
t
Fλ x n + Vλ x n−1
T
(n = 1,2,...).
(7)
In order to obtain a solution of problem (1) using this method, we will consider the
following theorem.
Theorem 1. If
α =1−
1
T

λ (T )
0
K 1 (σ ) σ d σ ≠ 0 ,
 1 λ (T )
 λ (T )
q = 
| K 1 (σ ) | dσ + 1  | K 1 (T , σ ) | dσ < 1,

|α | 0
 0
then the limit of the modified successive approximations
x n (t ) = h (t ) +
t
t
Fλ V λ x n −1
Fλ h + V λ x n −1 +
Tα
Tα
converges to the solution of the problem (1) and the convergence speed is
determined by
|| xn − x || ≤ q n || x − x0 ||
or
|| xn − x || ≤
qn
|| x1 − x0 || .
1− q
Proof. In order to obtain the approximation of xn (t ) we will use the auxiliary
equation
y(t ) = hˆ(t ) +
t
Fλ y.
T
(8)
Let Fλ y = c .
Then,
t
y(t ) = hˆ(t ) + c.
T
If we use Eq. (9) in Eq. (8), then we obtain
Ocak 2010 Cilt:18 No:1 Kastamonu Eğitim Dergisi
(9)
The Two Method on Equatıon Wıth Retarded Argument ...
93
 1

ˆ
1 − Fλ t  c = Fλ h
 T

that α = 1 − (1 / T ) Fλ t ≠ 0,
for c . By hypothesis we know
therefore
c = (1 / α ) Fλ hˆ and we can write
t
y = hˆ(t ) +
Fλ hˆ.
Tα
If we consider hˆ(t ) = h(t ) + Vλ x n −1 and use Eq. (7), then we have
t
t
Fλ h + Vλ xn−1 +
Fλ Vλ xn −1 (10)
Tα
Tα
Now, we will show that the approximations {xn (t )} , which are defined by Eq.
xn ( t ) = h ( t ) +
(10), converge to the solution of integral equation (5). Let us write
 t

Fλ Vλ + Vλ  x.
Ωx = 
T
α


Therefore, we write the approximations of Eq. (10) as
xn (t ) = h +
t
Fλ h + Ωxn−1
Tα
(n = 1, 2,3,...).
(11)
Thus, Eq. (5) can be written as
x =h+
t
Fλ h + Ωx.
Tα
(12)
Hence, the modified succesive approximations of Eq. (10) are similar to the ordinary
successive approximations (12) which are equivalent to the integral equation (5). In
order to show the convergence of approximations (10) to Eq. (5) we must prove the
convergence of approximations (11) to Eq. (12). If the condition
|| Ωx || ≤ || x || (q < 1) ,
is satisfied then ordinary successive approximations (11) converge to the solution of
Eq. (12) and the convergence speed is determined by
|| xn − x || ≤ q n || x − x0 ||
or
|| xn − x || ≤
qn
|| x1 − x0 || .
1− q
By this hypothesis we have q < 1 and
January 2010 Vol:18 No:1 Kastamonu Education Journal
Arzu AYKUT ...
94
| Ωx | =
1 λ (T )
| K1 (σ )|
| α | 0
(
λ (σ )
0
)
| K (σ ,τ ) | x(τ ) | dτ dσ + 
λ (T )
0
| K (T , σ ) | x(σ ) dσ
 1 λ (T )
 λ (T )
≤
| K1 (σ )| dσ + 1   | K (T ,τ ) | dτ || x ||,

| α | 0
 0
so we write
|| Ωx || ≤ q || x || .

If we substitue right side of equation (6) instead of
equation (6) then we obtain
x in the operator Vλ x to
t
t
x(t ) = h(t ) + Vλ h +  + Vλ  Fλ x + Vλ2 x (13)
T
T
2
If we rewrite the right side of equation (6) instead of x in the operator Vλ x to
equation (13) then we have
t
t
t
x(t ) = h(t ) + Vλ h + V 2 λ h +  + Vλ + V 2λ  Fλ x + Vλ3 x
T
T
T
(14)
Whene this operation is applied of n time we have
n
n
i =0
i =0
x =  Vλi h +  Vλi
t
Fλ x + Vλn +1 x
T
n
n
If we choose
hn (t ) =  Vλi h ,
i =0
an (t ) =  Vλi
i= 0
t
T
then it becomes
x = hn (t ) + an (t ) Fλ x + Vλn +1 x
(15)
Now we can proof that the formula it is true
| Vλn x |≤
for the operator
Ocak 2010 Cilt:18 No:1 Kastamonu Eğitim Dergisi
[ K λ (T )]
n!
n
(n ∈ N )
(16)
The Two Method on Equatıon Wıth Retarded Argument ...
Vλ x ≡ − 
λ (t )
0
95
K (t , s) x ( s ) ds
(0 ≤ t ≤ T )
(17)
n +1
As a result of this we neclect the operator | V λ x | in equation (15) for n ’s which
are big enough. Thus the consecutive approximations are formed by taking the Volterra
operator into consideration.
xn (t ) = hn (t ) + an (t ) Fλ xn
Theorem 2: Let
problem (1) and
τ (t ) ≥ 0, a(t ), f (t ) (0 ≤ t ≤ T ) be
αn = 1− 
λ (T )
0
(18)
the functions given in
K1 ( s ) hn ( s ) ds ≠ 0 .
Also
n
[ K λ (T )]
=0
n!
lim An
such that
n →∞
An = 1 +
|| an || λ (T )
| K1 ( s) | d s
| α n | 0
Then. the limit of the approximations
x n (t ) = h n (t ) +
a n (t )
αn

λ (T )
0
K 1 ( s ) hn ( s ) ds
converges to the solution of problem (1) and the speed of the convergence is
determined by
[ Kλ (T )]
| x n (t ) − x(t ) | ≤ An
n!
n
Proof: Eq. (18) is the Fredholm integral equation with a degerenated kernel.The
solution of
xn (t ) = hn (t ) + 
λ (T )
0
an (t ) K1 (s ) xn ( s ) ds
(19)
is the same as the solution of eq. (15) and problem (1). Now, let us find the solution
of equation (19). So, we use auxiliary equation,
y(t ) = hn (t ) + a n (t ) Fλ y
where Fλ y is shown as Fλ y = cn .Thus y(t ) is like that
January 2010 Vol:18 No:1 Kastamonu Education Journal
Arzu AYKUT ...
96
y(t ) = hn (t ) + an (t ) cn
(20)
Therefore,
cn = 
λ (T )
0
When
αn =1− 
λ (T )
0
K 1 ( s ) hn ( s ) ds + c n

λ (T )
0
K 1 ( s ) a n ( s) ds
K 1 ( s ) hn ( s ) ds ≠ 0 is given cn is found as follows
cn =
If we use equation (21) in (20), for
1
αn
n = 1,2,...
xn (t ) = hn (t ) +

λ (T )
0
K1 ( s ) hn ( s ) ds
(21)
then
an (t )
αn

λ (T )
0
K1 ( s ) hn ( s ) ds
(22)
This operation is the approximate solution of problem(1) that is, the limit of x n (t )
converges to the solution of problem (1).
Now let us determine the error of the approximate solution of eq. (22). Using (15)
and (18), we reach
x − x n = a n ( t ) F λ ( x − x n ) + V λn + 1 x
If it is acceted that ε is ε = x − x n , then we obtain the Fredholm integral
equation with a degenerated kernel
ε = an (t ) Fλ ε + Vλn+1 x
(23)
It was proven that solution of equation (23) is being found by using the following
formula:
ε = Vλn+1 x +
a n (t )
αn

λ (T )
0
K 1 ( s ) V λn +1 x ( s ) ds
Thus, we write
| ε | ≤ [1 +
|| a n || λ (T )
| K 1 ( s ) | ds ] || V λn +1 x ( s ) ||
| α n | 0
Then, by the hypothesis,
An = 1 +
|| a n || λ (T )
| K 1 ( s ) | ds
| α n | 0
Ocak 2010 Cilt:18 No:1 Kastamonu Eğitim Dergisi
The Two Method on Equatıon Wıth Retarded Argument ...
97
and we have
n
| xn (t ) − x(t ) | ≤ An
[ K λ (T )]
|| x ||
n!
(24)
Example 1. Let us consider the boundary value problem:
1
1 3
t ) = t 2 − t 2 0 ≤ t ≤ 1),
(25)
2
2
x(t ) = 0 (−1/16 ≤ t ≤ 0), x(1) = 1
x′′(t ) + tx(t −
This equation can be written as the Fredholm-Volterra integral equation
x (t ) =
−
409 1 4 2 72 t 1/ 2 
3 + 28σ − 80σ 2 
t + t − t +  3 + 4σ − 16σ 2 +
 x(σ ) dσ
420 12
35
16 0 
1 + 16σ 
1 t−
16 0
t /2

(4t − 1) + (48t − 20)σ − 80σ 2 
2
(4
t
1)
(16
t
12)
σ
16
σ
−
+
−
−
+

 x(σ )dσ .
1 + 16σ


(26)
Let
h (t ) =
K1 (σ ) =
K (t , σ ) =
409 1 4 2 72
t+ t − t ,
420 12
35
1
3 + 28σ − 80σ 2 
2
3
+
4
−
16
+
σ
σ
,
16 
1 + 16σ 
1
(4t − 1) + (48t − 20)σ − 80σ 2 
2
(4
t
−
1)
+
(16
t
−
12)
−
16
+
σ
σ

16 
1 + 16σ

and
1/ 2
Fλ x ≡  K1 (σ ) x(σ ) dσ ,
0
Vλ x ≡ − 
t− t / 2
0
K (t , σ ) x(σ )dσ .
Therefore, the integral equation (19) can be written as
x(t ) = h(t ) + tFλ x + Vλ x
(27)
and this equation is equivalent to problem (25). Some values of the solution of this
equation are obtained by using the method of modified successive approximations and
January 2010 Vol:18 No:1 Kastamonu Education Journal
Arzu AYKUT ...
98
the method of consecutive approximations of order two which are given in Table 1,
where the first approximation is x 0 (t ) = ( 409 / 420)t.
Table 1. Values at some point inthe interval [ 0,1]
ti
x(t i )
x 2( 2) (t i )
x 2( 3) (t i )
ε 1 (t i )
ε 2 (t i )
0.00
0.00
0.0000000
0.0000000
0.000000
0.000000
0.25
0.25
0.2501132
0.2501078
0.000113
0.000107
0.50
0.50
0.5000794
0.5000684
0.000079
0.000068
1.00
1.00
1.0000013
0.9999046
0.000001
-0.000095
x2(2) : The modified successive method; x2(3) : The concecutive substitution method.
ε1
and ε 2 are speed of the modified successive method and the concecutive
substitution method, respectively.

1. Norkin, S.B., Differential equations of the second orderwith retarded argument
some problems of theory of vibrations of systems with retardation , A. M. S.,
1972.
2. Mamedov, Ja. D., Numerical Analysis, Atatürk Üniversitesi (in Turkish), 1994.
3. Krasnosel’skij, M.A., . Lifshits, Je. AA., Sobolev ,V., Positive Linear Systems,
Heldemann, Berlin, p. 153., 1989.
4. Aykut, A., Yıldız, B., On a boundary value problem for a differential equation
with variant retarded argument, Appl. Math. Comput.93, 63-71, 1998
Ocak 2010 Cilt:18 No:1 Kastamonu Eğitim Dergisi