1. yapısal kırılma testleri

1. YAPISAL KIRILMA TESTLERİ
Yapısal kırılmanın araştırılması için CUSUM, CUSUM-Square ve CHOW testleri bize gerekli bilgileri
sağlayabilmektedir.
1.1. CUSUM Testi
(Cumulative Sum of the recursive residuals – Ardışık hataların kümülatif toplamı.)
Ardışık hatalar ile hesaplanan bu test veri setinde kırılmanın olup olmadığı hakkında kabaca bilgi verir.
Hangi dönemde kırılma olduğu hakkında net bir bilgi vermez. Bunun için birazdan aşağıda
göreceğimiz CUSUM-Square ve Chow testlerinden faydalanacağız.
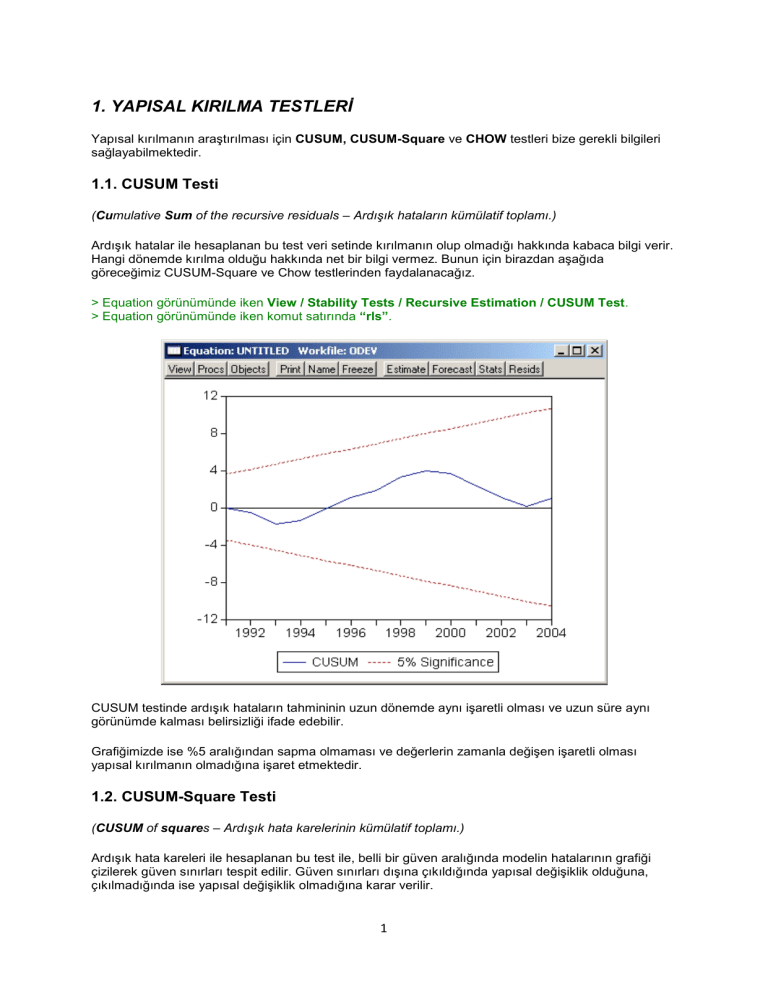
> Equation görünümünde iken View / Stability Tests / Recursive Estimation / CUSUM Test.
> Equation görünümünde iken komut satırında “rls”.
CUSUM testinde ardışık hataların tahmininin uzun dönemde aynı işaretli olması ve uzun süre aynı
görünümde kalması belirsizliği ifade edebilir.
Grafiğimizde ise %5 aralığından sapma olmaması ve değerlerin zamanla değişen işaretli olması
yapısal kırılmanın olmadığına işaret etmektedir.
1.2. CUSUM-Square Testi
(CUSUM of squares – Ardışık hata karelerinin kümülatif toplamı.)
Ardışık hata kareleri ile hesaplanan bu test ile, belli bir güven aralığında modelin hatalarının grafiği
çizilerek güven sınırları tespit edilir. Güven sınırları dışına çıkıldığında yapısal değişiklik olduğuna,
çıkılmadığında ise yapısal değişiklik olmadığına karar verilir.
1
Cusum Square testi ile yapısal kırılmanın dönemi de tespit edilir.
> Equation görünümünde iken View / Stability Tests / Recursive Estimation / CUSUM of Squares
Test.
> Equation görünümünde iken komut satırında “rls”.
Grafiğimizde belirtilen aralık dışına sapma olmamıştır. Bu yüzden yapısal kırılmadan söz edilemez.
1.3. CHOW Testi
Bu test ile regresyon modelinde yapısal kırılmanın varlığını araştıracağız. Eğer incelenen dönemde
belirli bir tarihten itibaren yapısal değişiklik varsa, yani verilerde belirli bir tarihte başlayan ve bir süre
devam eden bir kırılma söz konusuysa, modelin kırılma öncesi ve kırılma sonrası dönemlerini ayrı ayrı
tahmin etmek gerekir.
Chow testinin uygulanabilmesi için bazı varsayımlar sağlanmalıdır:
- Her iki alt döneme ait hata terimi de sabit varyanslı olmalı.
- Kısıtsız modellerin hata terimleri birbirinden bağımsız olmalı.
- Kırılmanın oluştuğu dönem bilinmeli.
- Oluşturulan her iki dönemin gözlem sayısı parametre sayısından büyük olmalı. (Eğer gözlem
sayıları parametre sayısından küçükse Chow Predictive testi uygulanır.)
Bizim testlerimizde kırılma görülmemesine rağmen deneme amaçlı olarak 1995 yılında sapma
meydana geldiğini varsayalım. Bu durumda veri setini “1995 öncesi” ve “1995 ve sonrası” şeklinde
iki bölüme ayıracağız.
2
2
Chow testi uygulanmadan önce bu iki alt döneme ait varyansların (s1 , s2 ) eşitliği testi de yapılmalıdır:
(1987-1994) VADELI = α0 + α1 LOG_FAIZ + α2 LOG_GSMH + α3 LOG_DOVIZ , SSR1 n1 = 8
(1995-2004) VADELI = β0 + β1 LOG_FAIZ + β2 LOG_GSMH + β3 LOG_DOVIZ , SSR2 n2 = 10
2
2
2
H0: s1 = s2
2
2
H1: s1 ≠ s2
2
2
Varyansların eşitliği F testi ile sınanacaktır. F formülünde s değerleri bilinmediği için Se değerlerini
kullanacağız.
s = e / (n-k) k: 4 (Parametre adedi)
2
2
Öncelikle modeli ikiye ayırıp regresyon ile tahmin yapmamız gerekiyor:
> Veri aralığı seçmek için Quick / Sample / “1987-1994”
> Komut satırında “smpl 1987 1994”
1987-1994 ve 1995-2004 aralıkları için regresyon çözümü aşağıdaki tablolardaki gibidir.
smpl 1987 1994
ls LOG_VADELI c LOG_GSMH LOG_DOVIZ LOG_TEFE
Dependent Variable: LOG_VADELI
Method: Least Squares
Date: 02/07/06 Time: 17:02
Sample: 1987 1994
Included observations: 8
Variable
Coefficient Std. Error
t-Statistic
Prob.
C
-2.010969
3.727106
-0.539552
0.6181
LOG_GSMH
1.154336
0.309462
3.730132
0.0203
LOG_DOVIZ
-0.282821
0.396849
-0.712665
0.5154
LOG_TEFE
0.312116
0.228560
1.365576
0.2438
R-squared
0.996069
Mean dependent var
4.051069
Adjusted R-squared
0.993120
S.D. dependent var
1.329593
S.E. of regression
0.110285
Akaike info criterion
1.264652
Sum squared resid
0.048651
Schwarz criterion
1.224931
Log likelihood
9.058606
F-statistic
337.8105
Durbin-Watson stat
2.027497
Prob(F-statistic)
0.000029
3
smpl 1995 2004
ls LOG_VADELI c LOG_GSMH LOG_DOVIZ LOG_TEFE
Dependent Variable: LOG_VADELI
Method: Least Squares
Date: 02/07/06 Time: 17:04
Sample: 1995 2004
Included observations: 10
Variable
Coefficient Std. Error
t-Statistic
Prob.
C
5.381369
5.284752
1.018282
0.3478
LOG_GSMH
0.765300
0.631230
1.212395
0.2709
LOG_DOVIZ
0.394419
0.540712
0.729444
0.4932
LOG_TEFE
-0.310629
0.118177
-2.628505
0.0391
R-squared
0.992573
Mean dependent var
9.554720
Adjusted R-squared
0.988859
S.D. dependent var
1.502069
S.E. of regression
0.158542
Akaike info criterion
0.556418
Sum squared resid
0.150814
Schwarz criterion
0.435384
Log likelihood
6.782092
F-statistic
267.2847
Durbin-Watson stat
1.115667
Prob(F-statistic)
0.000001
1987-1994:
LOG_VADELI = -2.010968505 + 1.154335821*LOG_GSMH - 0.2828207368*LOG_DOVIZ +
0.3121158732*LOG_TEFE
SSR1: 0.048651
n1: 8
2
s1 = 0,048651 / (8-4) = 0,01216275
1995-2004:
LOG_VADELI = 5.381369155 + 0.7653001569*LOG_GSMH + 0.3944188306*LOG_DOVIZ 0.3106293338*LOG_TEFE
SSR2: 0.150814
n2: 10
2
s2 = 0,150814 / (10-4) = 0,0251357
F = 0,0251357 / 0,01216275 = 2,07 Ftablo = 5,91
Ftest < Ftablo olduğundan Ho reddedilemez. Yani dönemlerin varyansı eşittir. Bu durumda Chow testi
uygulanabilir.
4
> Veri aralığını ilk haline getirmek için “smpl @all”
Buraya kadar aslında Chow testinin uygulanabilirliğini araştırmış olduk. Asıl test kısmı aşağıda
gerçekleştirilmektedir. Tabii ki aslında Chow testini yapabilmek için CUSUM-Square ve yukarıdaki
diğer testler yardımıyla belli bir tarihte kırılma gözlememiz gerekiyordu. Yine biraz önce modeli iki
parçaya bölmüş olmamızın gerçekten bir anlamı olması gerekiyordu.
1995 yılında kırılma olduğunu varsaymaya devam ederek Chow testine geçelim.
VADELI = δ0 + δ1 LOG_FAIZ + δ2 LOG_GSMH + δ3 LOG_DOVIZ ise SSRt n = 18 (Kısıtlı model)
VADELI = α0 + α1 LOG_FAIZ + α2 LOG_GSMH + α3 LOG_DOVIZ ise SSR1t n1 = 8 (1987-1994)
VADELI = β0 + β1 LOG_FAIZ + β2 LOG_GSMH + β3 LOG_DOVIZ ise SSR2t n2 = 10 (1995-2004)
k: 2 (Kısıt adedi.)
H0 : α0 = β0 , α1 = β1 , α2 = β2 , α3 = β3
H1 : α0 ≠ β0 | α1 ≠ β1 | α2 ≠ β2 | α3 ≠ β3 (en az biri farklı)
SSR : 0.314403
SSR1: 0.048651
SSR2: 0.150814
Ftest > Ftablo olduğundan Ho reddedilir. Yani iki denklemin parametrelerinin eşit olmamasından,
dolayısıyla yapısal değişim olduğundan sözedilebilir. Tabii ki diğer şartların sağlanmadığı bir durumda
bu testin doğrudan yapılıp yorumlanması bir anlam taşımamaktadır.
5
2. YAPISAL DEĞİŞİMİN KUKLA DEĞİŞKENLE DÜZELTİLMESİ
Kukla değişken yardımıyla hem yapısal değişiklik olup olmadığını, hem de bu değişikliğin sabit
terimden mi yoksa eğim teriminden mi kaynaklandığını öğrenebiliriz. Yukarıda 1995 yılında yapısal
değişiklik olduğunu varsayarak devam etmiştik.
Bu nedenle 1987-1994 dönemlerine 0, 1995-2004 dönemlerine 1 değerleri verilerek bir kukla değişken
oluşturalım.
Yıllar
1987
1988
1989
1990
1991
1992
1993
1994
1995
1996
1997
1998
1999
2000
2001
2002
2003
2004
DK1
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
Bu şekilde oluşan LOG_VADELİ = f ( LOG_GSMH, LOG_DÖVİZ, LOG_TEFE, DK1 ) modeli için
regresyon çözümü aşağıdadır.
LOG_VADELİ = f ( LOG_GSMH, LOG_DÖVİZ, LOG_TEFE, DK1 )
ls LOG_VADELI c LOG_GSMH LOG_DOVIZ LOG_TEFE DK1
Dependent Variable: LOG_VADELI
Method: Least Squares
Date: 02/07/06 Time: 19:20
Sample: 1987 2004
Included observations: 18
Variable
Coefficient Std. Error
t-Statistic
Prob.
C
6.880479
1.449690
4.746174
0.0004
LOG_GSMH
0.554678
0.189052
2.934001
0.0116
LOG_DOVIZ
0.574175
0.191766
2.994146
0.0104
LOG_TEFE
-0.289474
0.083354
-3.472829
0.0041
DK1
0.155040
0.161598
0.959420
0.3549
0.998245
Mean dependent var
7.108653
Adjusted R-squared 0.997705
S.D. dependent var
3.137099
S.E. of regression
0.150285
Akaike info criterion
0.722430
Sum squared resid
0.293614
Schwarz criterion
0.475104
Log likelihood
11.50187
F-statistic
1848.628
Durbin-Watson stat
1.092349
Prob(F-statistic)
0.000000
R-squared
DK1 Prob. = 0.3549 > 0.05 olduğu için DK1 anlamsız.
Görüldüğü gibi DK1 kukla değişkeninin eklenmesi anlamlı değildir. Zaten yukarıdaki testler de böyle bir
değişkene ihtiyaç olmadığı sonucunu vermişlerdi.
6
(Kukla eklenmemiş orjinal model için)
(Kukla eklenmiş yeni model için)
Her iki durumda yapısal kırılma gözlenmiyor.
7
NOT: VERİ SETİ
Vadeli
Mevduat
Vadesiz
Mevduat
Faiz
GSMH
Yıl Ortası
Nüfus
Kişibaşı
GSMH
TEFE
Döviz
Kuru
(milyon tl)
(milyon tl)
(%)
(milyon tl)
(milyon)
(tl)
(%)
(tl)
1987
8,13
6,23
52,00
129,22
52,56
2,46
32,19
0,0009
1988
15,71
7,60
83,90
227,32
53,72
4,23
68,22
0,0014
1989
27,99
12,26
58,83
393,06
54,89
7,16
69,43
0,0021
1990
41,77
18,89
59,35
630,12
56,20
11,21
54,67
0,0026
1991
76,19
27,38
72,70
1093,37
57,31
19,08
58,16
0,0042
1992
126,64
46,13
74,24
1981,87
58,40
33,94
65,53
0,0069
1993
186,85
74,50
74,76
3868,43
59,49
65,03
64,02
0,0110
1994
441,29
127,01
95,56
7762,46
60,58
128,14
118,47
0,0298
1995
971,67
195,88
92,32
14772,11
61,64
239,64
88,01
0,0457
1996
2131,21
566,40
93,77
28835,88
62,70
459,92
78,66
0,0814
1997
4293,19
893,14
96,56
52224,95
62,48
835,87
80,75
0,1521
1998
9250,48
1402,46
95,50
77415,27
63,46
1219,93
70,14
0,2610
1999
17882,46
2822,66
46,73
124583,46
64,35
1936,18
52,79
0,4201
2000
24805,61
4209,97
45,64
178412,44
67,46
2644,68
50,65
0,6237
2001
36329,20
6376,65
62,50
277574,06
68,62
4045,21
66,16
1,2254
2002
46721,93
7914,97
48,19
359762,93
69,63
5167,08
51,32
1,5058
2003
61036,06
11418,45
28,59
430511,48
70,71
6088,24
23,84
1,4931
2004
82830,98
14338,41
22,06
353980,19
71,79
4930,84
12,21
1,4223
Yıllar
Değişkenler:
Vadeli Mevduat (VADELİ): Bağımlı değişkenimiz, bankalarda aylık vadelerle işlem gören
mevduatların yıllık karşılığıdır.
Vadesiz Mevduat (VADESİZ): Bankalardaki vadesiz mevduatların yıllık karşılığıdır.
Faiz Oranı (FAİZ): 12 ay vadeli ağırlıklandırılmış mevduat faiz oranlarının yıllık karşılığıdır. (TCMB
notu: Mevduat faiz oranlarında, bankaların vadeler itibariyle ilgili ay içinde uygulayacağını bildirdiği
azami faiz oranlarının mevduat tutarları ile gün sayısına göre ağırlıklandırılarak hesaplanmış
ortalamaları alınmaktadır.)
Kişibaşı GSMH (GSMH): Yıl içinde kişibaşına düşen gelir karşılığını ifade etmektedir. Toplam
GSMH’nin yıl ortasındaki ortalama nüfus değerine bölünmesiyle elde edilir. (TCMB notu: Yıl ortası
nüfus değerleri; 1990-1996 yılları 1985-1990 nüfus projeksiyonu, 1997-1999 yılları 1997 yılı nüfus
tespiti, 2000-2004 ise 2000 yılı genel nüfus sayımına göre verilmiştir.)
TEFE (TEFE): Toptan eşya fiyatlarındaki yıllık yüzde değişimleri ifade etmektedir.
Döviz Kuru (DÖVİZ): Yıl içindeki ortalama dolar kurunun TL karşılığıdır.
8