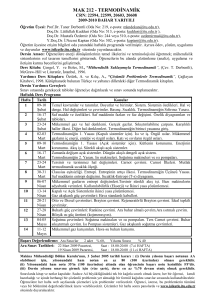
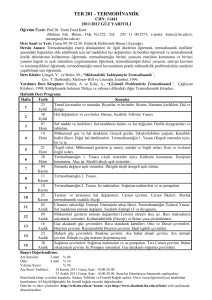
Donetsk Milli Mikhail Tugan Baranovskogo Ekonomi
ve Ticaret Üniversitesi (DETÜ)
Soğutma ve ticari makineleri bölümü
Dersin konusu:
Termodinamiğin İkinci Yasası ve onu
uygulaması
Öğt. Doç. Karnaukh Viktoriia
Donetsk-Adana
2015
PLAN:
1.
2.
3.
4.
5.
6.
Termodinamiğin ikinci yasasının ifadeleri;
Cadi Carnot çevrimi – ısı makinelerinin ideal çevrimidir;
Düzensizlik ve Entropi;
Carnot soğutma çevrimi nedir?
Pistonlu motorların teoretik çevrimleri;
Soğutma makineleri ve ısı pompası çevrimleri.
ÖNERİLEN KAYNAKLAR:
1. Çetinkaya Selim “Termodinamik”.2. Basım. NobelKitap. Ankara, 2011.
2. Akdağ Mustafa “Temel kavramları ile mühendislik termodinamiği”.
Kafqaz Üniversitesi yayınları, Bakü, 2009.
1. Termodinamiğin ikinci yasasının ifadeleri
19.
yy’ın
başlarında
buhar
makinesini
geliştirme
calışmalarında az yakıt kullanılarak daha cok iş elde etme, hatta hic
yakıt kullanmadan, cevreden ısı almak amacıyla, surekli calışan
makine yapma denemeleri yapılıyordu.
İlk defa Sadi Carnot, makine ve akışkan cinsine bağlı olmaksızın, ısıdan
faydalı iş elde etme fikrini, en genel şekilde ele aldı ve calışmalarının
sonucunda Termodinamiğin ikinci yasasının temelini oluşturacak şekilde,
• Isının ağırlığı olmayan bir madde olduğu ,
• Isının ancak sıcak olan kaynaktan, soğuk olan
kaynağa doğru kendiliğinden gectiği,
• İki kaynak arasında sıcaklık farkı varsa,
orada mekanik iş elde edilebileceği, buna
karşılık mekanik iş tuketme karşılığında
orada sıcaklık farkının oluşturulabileceği,
• Termik makinelerin calıştırılabilmesi icin
mutlaka sıcaklıkları birbirinden farklı iki
kaynağa ihtiyac olduğu…
fikirleri ile tersinir
makine kavramını ilk
defa ortaya koyuyordu
Termodinamiğin 2. yasası çeşitli biçimlerde ifade edilmiştir.
İngiliz bilim adamı Lord Kelvin şöyle bir ifade sunmuş:
Periodik olarak çalışan ve bir tek ısı kaynağı ile ısı alış verişi yaparak
sürekli olarak iş üreten bir makinenin yapılması mümkün
değildir.
Kaynaklardan çoğunda yükardaki ifade Kelvin-Plank olarak bilinir, onun
anlamına göre
hiçbir ısı makinesinin ısıl verimi % 100 olamaz.
Bu suretle, «ikinci türü ‘perpetuum mobile’nin» yapılması mümkün değildir.
Bir ısı makinesinin sürekli çalışabilmesi için sıcak kaynaktan ısı alınmasının
yanısıra soğuk kaynağa da belirli miktarda ısı vermesi gerekir.
Clausius ifadesi ise, Çerede hiçbir etki bırakmaksızın ısıyı soğuk ısı
kaynagından sıcak ısı kaynağına ileten bir ısı pompası (veya
soğuk makinesi) yapmak mümkün değildir
ya da bir başka ifadeyle
Isı enerjisi kendiliğinden soğuk ortamdan sıcak ortama doğru
akamaz, biçimindedir.
Yasanın en önemli sonuçlarından biri ise,
Kapalı sistemlerde ısı enerjisi hiçbir zaman tümüyle diğer bir enerji
formuna (örneğin mekanik enerjiye) dönüşmez. Isı enerjisi, sıcaklığı yüksek
olan cisimlerden düşük olanlara doğru akar. Bu süreç tersinmezdir.
Yani dışardan yardım olmadan ısı, düşük sıcaklıktaki cisimden yüksek
sıcaklıktaki cisme ısı aktarmak mümkün olmaz.
2. Cadi Carnot çevrimi – ısı makinelerinin ideal çevrimidir
1824 yılında Fransız bilim adamı Cadi Carnot
tarafından ısı makinelerinin IDEAL Çevrimi olarak
ortaya konmuş ve Emile Clapeyron tarafından 1830 ve
1840’lı yıllarda geliştirilmiştir.
Carnot çevriminin p-v ve T-s diyagramı, Şekil 1’de
görüldüğü gibi.
Carnot, ideal içten yanmalı motorun konseptini
geliştirdiği sırada izotermik dönüşümün ideal ısı alması
dönüşümü olduğunu ortaya koydu. Bu sırada tün
verildiği ısı tam işe dönüşür (1. Şek).
Nicolas Léonard
Sadi Carnot
(1 Haziran 1796 –
24 Ağustos 1832)
Fransız fizikçi ve
matamatikçi
р
T
2
q1
q1
3 T1=const
2
dq=0
3
T1=const
l0
q0=q1-q2
T2=const
dq=0
1
q2
4
T2=const
v
1
4
q2
s1
s2
s
Şekil 1. Carnot çevriminin p-v ve T-s diyagramları:
1-2 – Adyabatik Sıkışma (s=c),
2-3 – İzotermik Genleşme (Т=с),
3-4 –Adyabatik Genleşme (s=c),
4-1 – İzotermik Sıkışma (T=c).
Termik faydalı çalışma katsayısı:
lçev qçev q1 - q2
q2
T2
t
1 1
q1 q1
q1
q1
T1
(2.1)
3 Düzensizlik ve Entropi
(2.1) no’lu formüle göre çevreye verilen ısı miktarı q2
q1
q2 T2
T1
İfade edilebilir, şöyle ki q1/T1 ve q2 doğru
orantılı niceliklerdir.
İlk defa 1865 yılında Alman bilimadamı Clausius’un tarafından q/T oranı
Entropi olarak adlandırılmış, ilk defa bu terimi ortaya koyulmuş.
Entropi, bir sistemdeki enerjinin değersizleşme düzeyini gösteren
bir büyüklüktür.
Entropinin fiziksel bir açıklamasını yapmak oldukça zor olmakla birlikte
‘Entropi, sistemdeki düzensizliğin bir ölçüsüdür’, biçiminde bir tanımlama
yapılabilir.
Düzensizlik arttıkça entropi de artmaktadır.
Bütün tersinir çevrimler için entropi değişimi sıfıra eşittir:
dq
0
ds
T
(3.1a)
ster sinir 0
(3.1b)
Ama eğer dq sabit ise tersinmez çevrimlerde tersinir çevrimlere göre
entropi değişimi sabit değil, yani artıyor ve:
dq
ds
T
(3.2a)
dqTds
(3.2b)
Yani tersinir durumlarda entropi 0'a eşitken tersinmez durumlarda entropi 0'dan
büyüktür.
Ancak gerçek hayatta tersinir sistem yoktur, gerçek olan tersinmez işlemlerin
ideallikten ne kadar uzak olduğunu refere etmek için oluşturulmuş hayali bir
işlemdir.)
Termodinamik işlem surasında cisim 1 durumundan 2 durumuna
geçiyor ve sonra ilk haline dönüyorsa bu sistem için entropi değişimi
integral formül biçimde yazılır:
2
(
1
q
T
2
) ds s2 s1 s
1
(3.3)
Herhangi termodinamik işlem sırasında verilen (alınan) ısı
miktarı ısı diyagramı sayesinde hesaplanabilir (T-s diyagramı).
Isı diyagramında dikey eksen sıcaklık, yatay dikey ise entropidir.
Bunu unutmamak lazım, ideal gazlar için entropi ile özgül ısı
arasında bağıntı var olduğunun yanı sıra her gazın özel özgün ısısı da vardır.
Bu yüzden her gaz için ayrı T-s diyagramı kullanılmalıdır.
Şekil 2’de bir termodinamik işlem sıcaklık-entropi diyagramı üzerinde
gösterilmiştir
Т
2
2
Fa12b q Tds
1
1
df
a
(3.4)
ds
Şekil 2. Bir termodinamik işlem
T-s diyagramı üzerindedir
b s
Adyabatik
sıkıştırma
Adyabatik
genleşme
Şekil 3. Oksijen gazı için T-s diyagramının parçası
İdeal gazlar için entropi değişimi
Bildiğiniz gibi Teknik Termodinamikte hesaplamalar mutlak entropi değil
entropi değişimi sayesinde yapılmaktadır. Normal koşullardaki (T273,15K, p-101,325 kPa) gazlar için entropi sıfıra eşittir (s=0).
Eğer özgül ısının sabit olduğunu varsayılırsa
T2
p2
s2 s1 c p ln R ln
T1
p1
p2
v2
s2 s1 cv ln c p ln
p1
v1
(3.5a)
(3.5b)
T2
v2
s2 s1 cv ln R ln
T1
v1
(3.5c)
Her termodinamik işlem için durum değişimi sırasında entropi değişimini
hesaplamak mümkündür.
T-sabit
sT s2 s1 R ln
T2
T1
V-sabit
sv s2 s1 cv ln
p-sabit
s p s2 s1 c p ln
T2
T1
p2
p1
v2
v1
p
sv s2 s1 cv ln 2
p1
sT s2 s1 R ln
s p s2 s1 c p ln
v2
v1
4. Carnot soğutma çevrimi nedir?
Termodinamiğin önemli uygulama alanlarından biri de soğutmadır. Soğutma,
soğutma makineleri veya ısı pompaları ile gerçekleştirilmektedir.
Soğutma makinesi, ısı makinesinin aksine, düşük sıcaklık kaynağından ısı
alarak yüksek sıcaklık kaynağına ısı transferini gerçekleştiren bir sistemdir.
Soğutma çevriminde kullanılan çalışma maddesine ‘soğutucu akışkan’ denir.
Eğer soğutma çevriminde soğutucu akışkanın hali değişir ise ‘buhar sıkıştırmalı
soğutma çevrimi’ denmektedir.
Eğer soğutma çevriminde hava soğutucu akışkan olarak kullanılır ise ‘hava
soğutma makinesi’ denmektedir.
İdeal olan soğutma makinesinin çevrimi olarak ters Karnot çevrimi kabul
edilmektedir.
Ters Karnot çevrimi iki adet izotermik ve iki adet adyobatik olmak üzere tam
dört kademeden oluşmaktadır (şekil 4).
T
р
3 q1
3
dq=0
q1
4
l0
T1=const
l0
2
q2
1
dq=0
T2=const
v
а
4 T1=const
T2=const
2
1
q2
s1
b
s2
s
Şekil 4. Ters Carnot çevriminin p-v ve T-s diyagramları:
1-4 – Adyabatik Sıkışma (s=c),
4-3 – İzotermik Sıkışma (Т=с),
3-2 –Adyabatik Genleşme (s=c),
2-1 – İzotermik Genleşme (T=c).
Ters Karnot çevriminin katsayısı (soğutma katsayısı)
karnot
q
aln
lharcanan
q2
T2
1
q1 q2 T1 T2
(4.1)
5. Pistonlu motorların teoretik çevrimleri
Isı makinenin çevrimi altı gruba ayırabilir
Sabit hacimli çevrim –
Otto çevrimi
Stirling çevrimi
Gaz türbinlerin çevrimi
– Brayton çevrimi
Sabit basınçlı çevrim –
Dizel çevrimi
Karma çevrim –
Trinkler çevremi
Buhar türbinlerin çevrimi –
Renkin çevrimi
b)
Şekil 5 - Pistonlu içten yanmalı motor:
a) ve b) kesitleri
a)
OTTO ÇEVRİMİLİ MOTOR (1887 yılında icat adilmiş)
р
3
Т
3
q1 v
q1v
2
l0
2
4
1
q2v
q2 v
1
AÖN
UÖN
a)
4
Otto Nikolaus Avgust
1832-1891
Alman mühendisi
v
ÜÖN
AÖN
s
b)
Şekil 6 – Otto çevrimi: a) çalışma diyagramında, b) termal diyagramda
Otto Çevrimi Safhaları :
1-2 – Adyabatik sıkıştırma: Bu safhada, piston alt ölü
noktadan üst ölü noktaya doğru hareket eder. Bu sırada
emme ve egzos valfleri kapalıdır, dolayısıyla içerdeki
hava+yakıt karışımı sıkışır ve basıncı grafikte görüldüğü
gibi artar.
2-3 – Sabit Hacimde Yanma: Piston üst ölü noktaya
ulaştığı sırada bujiden kıvılcım çaktırılarak sıkışarak
ısınmış hava+yakıt karışımı yanmaya başlar, bunun
sonucunda basınç p2'den p3 değerine sıçrama yapar.
3-4 – Genleşme: Bu safhada piston aşağı doğru
hareketine başlar. Bu durum 4 nolu noktaya kadar böyle
devam eder. Piston aşağı doğru hareketine devam
ettiğinden silindirdeki basınç da düşmeye başlar.
4-1 – Egzoz: Sistem 4 nolu noktaya (AÖN) geldiğinde
egzoz valfi açılır. Silindir egzoz sistemi ile dışarıya
açıldığından silindirdeki basınç atmosferik basınca düşer.
Sistemden ısının atılması bu safhada gösterilmiştir.
DİZEL ÇEVRİMİLİ MOTOR (1897 yılında icat adilmiş)
q1 p
p
2
3
Т
q1 p
3
l0
4
2
4
q2v
1
q2v
Rudolf Kristian Dizel
1858-1913
alman mühendisi
1
ÜÖN
AÖN
a)
v
ÜÖN
AÖN s
b)
Şekil 7 – Dizel çevrimi: a) çalışma diyagramında, b) termal diyagramda
Dizel Çevrimi Safhaları :
1-2 – Adyabatik sıkıştırma: Bu safhada, piston alt ölü noktadan üst
ölü noktaya doğru hareket ederek havayı sıkıştırıyor. Bu sırada
emme ve egzos valfleri kapalıdır.
2-3 – Sabit Basınçta Yanma. Bu safhada sıkıştırılan havanın
sıcaklığı 700-900°C'a ulaşır. Piston hareketinin en tepe
noktasında, dizel yakıt yüksek basınçla (atomizer memeden
geçerek) yanma odasının içerisine püskürtülür; burada sıcak
ve yüksek basınçlı hava ile karışır. Bu karışım hızla tutuşur ve
yanar.
3-4 – Genleşme: Bu safhada yanma odası içindeki gaz
genleşirerek piston aşağı doğru hareketine başlatırır. Bu
durum 4 nolu noktaya kadar böyle devam eder. Piston
aşağı doğru hareketine devam ettiğinden silindirdeki
basınç da düşmeye başlar.
4-1 – Egzoz: Egzoz gazını silindirin dışına atma ve taze
hava çekme işlemi.
TRİNKLER ÇEVRİMİLİ MOTOR (karma çevrimli motor)
(1904 yılında icat adilmiş)
qp
р
3
qp
Т
4
qv
2
qv
l0
3
4
5
Gustav Trinkler
1876-1957
rus mühendisi
2
5
1
qv
1
ÜÖN
AÖN
a)
v
ÜÖN
AÖN
s
b)
Şekil 8 – Karma çevrim: a) çalışma diyagramında, b) termal diyagramda
Karma Çevrim Kademeleri :
1-2 Sıkıştırma: Bu safhada, piston alt ölü noktadan üst ölü noktaya
doğru hareket eder. Bu sırada emme ve egzos valfleri kapalıdır,
dolayısıyla içerdeki hava sıkışır ve basıncı artar.
2-3 Sabit Hacimde Yanma: Piston üst ölü noktaya ulaştığı
sırada silindire enjektör tarafından yakıt püskürtülmeye başlar.
Sıkışarak ısınmış havayla karşılaşan yakıt yanmaya başlar, bunun
sonucunda basınç P2'den P3 değerine sıçrama yapar. Sisteme ısı
girişinin olduğu ilk safha bu safhadır.
3-4 Sabit Basınçta Yanma: Bu safhada piston aşağı doğru
hareketine başlar fakat yanma devam ettiğinden basınç
düşmez. Bu durum 4 nolu noktaya kadar böyle devam eder.
Böylece bu safhada da sisteme ısı girişi devam etmiş olur.
4-5 Genleşme: Artık silindire yakıt üskürtülmemektedir
ve yanma durmuştur. Piston aşağı doğru hareketine
devam ettiğinden silindirdeki basınç da düşmeye başlar.
5-6 Egzoz: Sistem 5 nolu noktaya (AÖN) geldiğinde egzoz valfi
açılır. Silindir egzoz sisitemi ile dışarıya açıldığından silindirdeki
basınç atmosferik basınca düşer. Sistemden ısının atılması bu
safhada gösterilmiştir.
Motor
Formül
Çalışma
maddesi
Sıkıştırma
katsayısı
Basınç
artması
katsayısı
Ön genleşme
katsayısı
Termik
faydalı
çalışma
katsayısı
v1
v2
Otto çevrimli
Dizel çevrimli
motor
motor
Yakıt+hava karışımı Yakıt+hava karışımı
(silindir dışında
(silindir içinde
yapılmaktadır)
yapılmaktadır)
6...12
14...25
Trinkler çevrimli motor
Yakıt+hava karışımı
13...20
р
3
р2
1,3...1,7
-
2
v3
v2
-
1,5...2,5
1,1...1,9
t 1
1
k 1
k 1
t 1 k 1
k ( 1 )
ητ 1
1
к 1
к 1
( 1) к ( 1)
Buhar türbinlerin çevrimi – Rankin çevrimi (1859 yılı)
Egzoz
gazları
Türbin
William John
Macquorn
Rankine
1820-1872
İngiliz bilim
adamı
Elektro
Jeneratör
yoğunlaştırıcı
Su
kazanı
Buhar
Soğuk su
Sıcak su
Kaynamış
su
Su pompası
Şekil 9 – Buhar türbinin prensip şeması
Bütün çağdaş buhar türbinlerin çalışmasının temelinde teoretik
Rankin çevrimi yer almaktadır.
Bu çevrimde ne sürtünme kaybıları, ne ısı kaybıları var, üstelik
bütün işlemler tersinmez işlemdir. Buna ek olarak, türbindeki buharın
genleşmesi izentropik sayılmaktadır.
T
Su kaynaması
ve buharın
oluşturması
Pompa
çalışması
х=0
Tkızgın
T2
1
2
1' 2'
х=1
5
4
3
T1
İzentropik buharın
genleşmesi
2"
Buharın
yoğunlaşması
6
4'
6'
s
Şekil 10 –Rankin çevriminin T-s diyagramı
Buhar türbininin çevriminin kademeleri:
2-3 – Çalışma akışkanı, düşük basıçtan, yüksek basınca pompalanır.
(İdeal şartlarda adyobatik olarak, yani ısı değişimi sıfır, yani entropi
değişimi sıfır) Pompalama için iş girişine ihtiyaç vardır.
(Örneğin mekanik veya elektirik işi).
3-4-5 – Yüksek basınçlı sıvı bir ısıtıcıya girer, bir ısı kaynağı ile sabit
basınçta kızdırılmış buhar halini alana dek ısıtılır.Genelde ısı kaynağı
olarak, kömür, doğal gaz veya nükleer güç kullanılır.
5-6 – Kızgın buhar, türbin boyunca genişler ve iş üretimine vesile olur.
İdeal şartlarda, bu genişleme izentropiktir. Bu olay buharın basınç ve
sıcaklık kaybetmesine sebep olur.
6-1-2 – Buhar daha sonra kondensere girer, doymuş sıvı
halini alana kadar soğutulur. Bu sıvı daha sonra tekrar pompaya girer ve
çevrim tekrar eder.
Termik faydalı çalışma katsayısı:
h5 h6
Rankin
qharcanan h5 h1
lalıl
6. Soğutma makineleri ve ısı pompası çevrimleri
Soğutma makinesinin çalışma prensip şeması şekil 11’de gösterilmektedir.
Çevredeki
ortam Qк
3
4
рyoğ, tyoğ
yoğuşturucu
3
4
kısılma
vanası
pbuh, tem.
2
1
evaporatör
2
Q0
pbuh, tbuh
1
Soğutulan
ortam
Şekil 11 – Soğutma makinesinin prensip şeması
kompresör
Çalışma maddesi (ısı taşıyıcı akışkan) olarak özel özelliğe sahip olan,
örneğin R134a, R600a, R22 maddeleri kullanılabilmektedir.
Bu maddelerin buharlaşması için sabit atmosfer basınçta ortam sıcıklığı
düşük olmalı (-15...-5oC), ama bu maddelerin buhar halinden sıvı
haline geçmesi için ortam sıcaklığı yüksek olmalıdır.
Çevrim kısaca, aşağıdaki kademeleri ihtiva etmektedir:
1. KADEME (2-1): taşıyıcı akışkanın buharlaşması - soğutulan ortamdaki
bulunan Qo ısısı, basınç ve sıcaklığı düşük olan taşıyıcı akışkana transfer
edilmektedir;
2. KADEME (1-4): taşıyıcı akışkanın sıkıştırılması - kompresör ünitesinde
taşıyıcı akışkan üzerine dışarıdan iş tatbik edilerek taşıyıcı akışkan yoğunlaşma
basıncına sıkıştırılmaktadır;
3. KADEME (4-3): taşıyıcı akışkanın yoğunlaştırması - basıncı ve sıcaklığı
yüksek olan taşıyıcı akışkanın, kondansatörde (yoğunlaştırıcıda) bünyesindeki Qk
ısısı ayrılmaktadır;
4. KADEME (3-2): taşıyıcı akışkanın genleşmesi - taşıyıcı akışkan capilary tube
(kısılma vanası)den geçerken onun basıncı ve sıcaklığı büyük ölçüde
düşürülmekte ve buharlaştırma kısmına geri döndürülmektedir.
Soğutma makineleri ve ısı pompaları aynı çevrime göre çalışmaları halde
kullanım amaçları farklıdır.
Soğutma makinelerinin kullanım amaçları, bir ortamdan ısı çekerek ortamı
çevre sıcaklığından düşük sıcaklıkta tutmaktır.
Isı pompalarının kullanım amaçları ise ısıtılan bir ortamın sıcaklığını
istenen düzeyde tutmaktadır.
Isı makinesinin prensip şeması
Sıcaklığı yüksek olan bir
kaynak
Soğutma makinesi ve Isı
pompasının prensip şeması
Sıcaklığı yüksek olan bir
kaynak
Q
Q
Lfaydalı
Çalışma
maddesi
Q0
Sıcaklığı düşük olan bir
kaynak
Lkullanılan
Çalışma
maddesi
Q0
Sıcaklığı düşük olan bir
kaynak
Isı pompasının çalışma prensip şeması şekil 12’de gösterilmektedir.
Şekil 12 – Isı pompasının çalışma prensip şeması
.
GÖSTERDİĞİNİZ İLGİ İÇİN
TEŞEKKÜR EDERİM!!!