6. Ders - 80.251.40.59

SAYISAL ĐNTEGRASYON
Sayısal olarak hesaplanacak integraller, sonlu [ a, b] aralığı üzerinde,
b
Ι( f ) = ∫ f ( x) ⋅d x
a
biçimindeki integraller olacaktır.Bu tür integralleri hesaplamak için çok sayıda sayısal yöntem vardır.
Bunların birçoğu f fonksiyonunun yerine yaklaşım fonksiyonlarının kullanılması esasına
dayanmaktadır. f fonksiyonu için bir yaklaşım ailesi,
{ f n : n ≥ 1}
olmak üzere,
n →∞
max f ( x) − f n ( x ) 
→0
a ≤ x ≤b
b
özelliğinin sağlanması istenmekte ve Ι ( f n ) =
∫f
n
( x )dx = Ι n ( f ) olmak üzere, Ι( f n ) kolay
a
hesaplanacak şekilde f n fonksiyonları seçilmektedir.
b
En ( f ) = Ι( f ) − Ι( f n ) = ∫ ( f ( x) − f n ( x) )dx
a
b
En ( f ) ≤ ∫ f ( x) − f n ( x) dx ≤ (b − a ) max f ( x) − f n ( x)
a ≤ x ≤b
a
Yamuk Kuralı
b
Ι( f ) = ∫ f ( x)dx integralini göz önüne alalım. Yamuk kuralı, f fonksiyonuna x = a, b
a
noktalarında polinom interpolasyonu yaklaşımına dayanmaktadır. f ( x ) yerine
f1 ( x ) =
( x − b)
a−b
⋅ f (a) +
( x − a)
b−a
⋅ f (b)
alınıp,
x−a
x−b

Ι( f1 ) = ∫ 
f (a) +
f (b) dx
b−a

a a −b
b
f (a) ( a − b )
f (b)
b−a
2
=−
⋅
+
⋅ (b − a ) =
⋅ [ f ( a ) + f (b) ]
a−b
2
b−a
2
2
elde edilir.
b
E ( f1 ) = E1 ( f ) = ∫ ( f ( x ) − f1 ( x ) )dx
a
Đnterpolasyonda hata ile ilgili sınır,
f ( x) − Pn ( x) = ( x − x0 ) ⋅ ( x − x1 ) ... ( x − xn ) ⋅
f n +1 (ξ x )
(n + 1)!
,
ξ x ∈ [ a, b ]
max f n +1 (ξ x ) = M n +1
a ≤ x ≤b
M n +1
(b − a)
f ( x) − Pn ( x) ≤ ( x − x0 ) ⋅ ( x − x1 ) ... ( x − xn ) ⋅
≤
⋅ M n +1
(n + 1)!
(n + 1)!
n +1
olup,
b
b
E1 ( f ) = ∫ ( f ( x) − f1 ( x )) ⋅ d x = ∫ ( x − a )( x − b)
a
a
f ′′(ξ x )
dx
2
,
ξ x ∈ [ a, b ]
f ıı (ξ )  −1
3
=
 ⋅ (b − a ) 
2  b

−(b − a )3
E1 ( f ) =
⋅ f ′′(ξ ) ,
12
ξ ∈ [ a, b ]
dır. Buna göre,
Ι ( f ) = Ι1 ( f1 ) + E1 ( f )
dır.
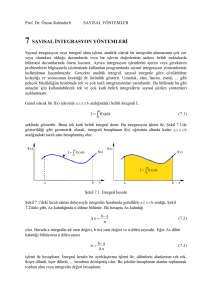
[ a, b] aralığının uzunluğu küçük olmadıkça yamuk kuralının kullanılabilir olmayacağı açıktır.
[ a, b] aralığı küçük uzunlukta alt aralıklara parçalanıp her biri üzerinde yamuk kuralı uygulanabilir.
[ a, b] genellikle eşit uzunluklu alt aralıklara parçalanır. [ a, b] aralığı n tane eşit uzunluklu alt aralığa
parçalansın. Her birinin aralık uzunluğu
xj
b
n
a
j =1 x j −1
Ι( f ) = ∫ f ( x)dx = ∑
b−a
= h olsun. x j = a + j ⋅ h , j=0,1,2,...,n için
n
∫
f ( x)dx
n
h

h3
= ∑  ⋅ ( f ( x j −1 ) + f ( x j ) ) − ⋅ f ′′(ξ j ) 
12
j =1  2

x j −1 ≤ ξ j ≤ x j
f (xj ) = f j
f ( x0 ) = f 0 
f ( x1 ) = f1 
 f 0 + f1 + f1 + f 2 + f 2 + f 3 + ... + f n − 2 + f n −1 + f n −1 + f n
.

= f 0 + 2 f1 + 2 f 2 + ... + 2 f n −1 + f n
.


.

f ( xn ) = f n 
gösterimleri altında,
b
n
Ι( f ) = ∫ f ( x)dx = ∑
a
Ι( f ) = Ι ( f n ) −
xj
∫
j =1 x j −1
f ( x)dx =
h
h3 n
⋅ [ f 0 + 2 f1 + 2 f 2 + ... + 2 f n −1 + f n ] − ⋅ ∑ f ′′(ξ j )
2
12 j =1
1 n

h3
⋅ n ⋅  ⋅ ∑ f ′′(ξ j ) 
12
 n j =1

,
ξ j ∈ ( x j −1 , x j )
min { f ′′( x)} ≤
a ≤ x ≤b
1 n
⋅ ∑ f ′′(ξ j ) ≤ max { f ′′( x)}
a ≤ x ≤b
n j =1
Amacımız hata için bir üst sınır bulmak. f fonksiyonu [ a, b ] ’de sürekli olduğundan;
1 n
⋅ ∑ f ′′(ξ j ) = f ′′(ζ ) , ζ ∈ [ a, b ]
n j =1
(ortalama değer teoremi)
h3 ⋅ n
⋅ f ′′(ζ ) , ζ ∈ [ a, b ]
12
b − a ) ⋅ h2
(
= Ι( f n ) −
⋅ f ′′(ζ ) , ζ ∈ [ a, b ]
12
Ι( f ) = Ι ( f n ) −
− (b − a ) ⋅ h2
En ( f ) =
⋅ f ′′ (ζ ) , ζ ∈ [ a, b ]
12
−h2
En ( f ) ≅
( f ′ ( b ) − f ′(a )) = E
n( f )
12
DEF FN F( x) = ...
INPUT a,b,n
s=0
h=(b-a)/n
FOR j=1 TO (n-1)
s=s+2*F(a+j*h)
NEXT j
I=(F(a)+s+F(b))*h/2
PRINT I
ÖRNEK:
1
f ( x) =
1 + x2
n = 1 için
Ι=∫
h
1  1
⋅ [ f 0 + f1 ] = ⋅ 1 +  = 0, 75
2
2  2
1 



h
1
1
Ι 2 ( f ) = ⋅ [ f 0 + 2 f1 + f 2 ] = 2 ⋅ 1 + 2 ⋅
+  = 0, 775
1 2
2
2 
1+

4

Ι1 ( f ) =
n = 2 için
n = 4 için
xj = a + j ⋅ h
h=
dx
π
= arctan1 = = 0, 7854
2
1+ x
6
0
1
1− 0 1
=
4
4
1 


h
2
2
2
1
4
Ι 4 ( f ) = ⋅ [ f 0 + 2 f1 + 2 f 2 + 2 f 3 + f 4 ] = ⋅ 1 +
+
+
+  = 0, 783
1
1
9 2
2
2 
1+
1+
1+

16
4
16

j=0,1,2,3,4
−h 2
E4 ( f ) =
⋅ ( f ′(b) − f ′( a ) )
12
1
−2 x
f ( x) =
⇒ f ′( x) =
2
2
1+ x
(1 + x 2 )
f ′(0) = 0 ,
f ′(1) =
−2 −1
=
4
2
2
1
− 
 4  ⋅  −1 − 0  = 1
E
4( f ) =


12
 2
 24 ⋅ 16
1
ÖRNEK: Ι =
dx
∫1+ x
integralinin yaklaşık değerini yamuk kuralıyla bulup, n=4 için hatanın yaklaşık
0
1
değerini ve hata için bir üst sınır bulmaya çalışalım. (Analitik çözüm:
dx
∫ 1 + x =ln2=0,69314)
0
Ι1 ( f ) = 0, 7500 , Ι 2 ( f ) = 0, 7083 , Ι3 ( f ) = 0, 7000 , Ι 4 ( f ) = 0, 6970
h=
b − a 1− 0 1
=
=
n
4
4
1
h
 4 2 4 1
Ι 4 ( f ) = ⋅ [ f 0 + 2 f1 + 2 f 2 + 2 f 3 + f 4 ] = 4 ⋅ 1 + + + + 
2
2  5 3 7 2
−h2
E
(
f
)
=
⋅ ( f ı (b) − f ı (a ) )
4
12
1
−1
f ( x) =
= (1 + x) −1 f ı ( x) =
1+ x
(1 + x) 2
b − a 1− 0 1
h=
=
=
n
4
4
1
−( ) 2
4 ⋅  −1 + 1 = −0, 004
E
4( f ) =


12  4

f ı (0) = −1
f ı (1) =
−1
4
Hata için üst sınır:
E4 ( f ) = −
( b − a ) ⋅ h 2 ⋅ f ′′(ζ )
12
ζ ∈ [ a, b ]
2
1
(1 − 0 ) ⋅  
 4  ⋅ M , M = max f ′′( x) , f ′′( x) = 2
E4 ( f ) ≤
, x=0 için max değerini alır
2
2
x∈[ 0,1]
12
(1 + x)3
E4 ( f ) ≤
( 0, 25 )
12
2
⋅2 =
1
= 0, 0104
96
SĐMPSON KURALI
b
Ι( f ) = ∫ f ( x)dx integralini göz önüne alalım.
a , c=
a
a+b
, b noktalarındaki
2
nterpolasyon polinomu,
P2 ( x) =
( x − b) ⋅ ( x − c)
( x − a) ⋅ ( x − c)
( x − a) ⋅ ( x − b)
⋅ f (a) +
⋅ f (b) +
⋅ f (c )
(a − b) ⋅ (a − c)
(b − a ) ⋅ (b − c )
(c − a ) ⋅ (c − b)
olmak üzere, f ( x ) yerine P2 ( x ) polinomunu alalım ve
b
Ι( P2 ) = ∫ P2 ( x)dx
a
integralini hesaplayalım. h =
P2 ( x) =
b−a
olsun. O zaman c = a + h, b = a + 2h olup,
2
( x − a − h ) ⋅ ( x − a − 2h )
2h
2
⋅ f (a ) +
( x − a ) ⋅ ( x − a − 2h )
−h
2
⋅ f (c ) +
( x − a) ⋅ ( x − a − h)
2h 2
⋅ f (b)
ve,
Ι( P2 ) =
h 
a+b

⋅  f (a) + 4 f (
) + f (b) 
3 
2

olur. [ a, b] aralığının uzunluğu büyük olduğunda aralığın parçalanması ve her bir parça üzerinde
yukarıdaki formül uygulanmalıdır. n çift sayı olmak üzere [ a, b] aralığını eşit uzunluklu alt aralıklara
parçalayalım.
h=
b−a
n
b
n
2
x2 j
a
j =1
x2 j−2
Ι n ( f ) = ∫ f ( x)dx = ∑
n
2
x2 j
∫
f ( x)dx
n
2
h
P2 ( x)dx = ∑ ⋅  f ( x2 j − 2 ) + 4 f ( x2 j −1 ) + f ( x2 j ) 
j =1 x2 j − 2
j =1 3
Ιn ( f ) ≅ ∑
∫
h
⋅ ( f 0 + 4 f1 + f 2 + f 2 + 4 f3 + f 4 + f 4 + 4 f 5 + f 6 + ... + f n − 2 + 4 f n −1 + f n )
3
h
= ⋅ ( f 0 + 4 f1 + 2 f 2 + 4 f 3 + 2 f 4 + 4 f 5 + 2 f 6 + ... + 2 f n − 2 + 4 f n −1 + f n )
3
=
h 4 ⋅ (b − a ) (4)
En ( f ) = −
⋅ f (ζ )
180
Hatanın yaklaşık değeri:
−h4
E
(
f
)
=
[ f ′′′(b) − f ′′′(a)]
n
180
ζ ∈ [ a, b ]
Đki Katlı Đntegraller
b d
Ι( f ) = ∫ ∫ f ( x, y )dydx integralini göz önüne alalım.
a c
b−a
=h
n
d −c
=l
m
I ji =
,
x j +1 yi+1
∫ ∫
x y
j
xj = a + j ⋅ h
,
yi = c + i ⋅ l
,
,
j=0,1,2,...,n
i=0,1,2,...,m
x j +1
f ( x, y )dydx =
i
l
∫x 2 ( f ( x, y ) + f ( x, y ) )dx
i
i +1
j
l h
= × ( f ( x j , yi ) + f ( x j , yi +1 ) + f ( x j +1 , yi ) + f ( x j +1 , yi +1 ) )
2 2
hl
= ( f ( x j , yi ) + f ( x j , yi +1 ) + f ( x j +1 , yi ) + f ( x j +1 , yi +1 ) )
4
bd
n −1 m −1
n −1 m −1
a c
j =0 i =0
j =0 i =0
Ι ( f ) = ∫ ∫ f ( x, y )dydx ≅ ∑∑ I ji = ∑∑ I ji ( f ( x j , yi ) + f ( x j , yi +1 ) + f ( x j +1 , yi ) + f ( x j +1 , yi +1 ) )