ESKİŞEHİR FATİH FEN LİSESİ GEOMETRİ

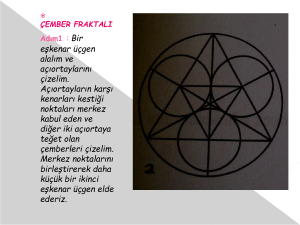
ESKİŞEHİR FATİH FEN LİSESİ
GEOMETRİ
OLİMPİYAT
NOTLARI
Eş Üçgenler
Derleyen
Osman EKİZ
EFFL
Matematik Öğretmeni
Yazım hataları mevcut olup. Tashihi yapılmamıştır. MY notlarından faydalanılmıştır.
Eş Üçgenler
Önce üçgen eşliğinde çok önem teşkil eden “eşleme yapma”
kavramını tanıyalım.
Şimdi bahsi geçmeyen üçüncü kenara ilişkin bir aksiyoma
ihtiyacımız var. Başrol oynayan açının karşısındaki kenara
taban denecek olursa,
Eşleme yapma. Eğer ABC ve ABC gibi iki üçgende A köşesine A, B köşesine B, C köşesine C köşesi karşılık getirilirse, bu iki üçgen arasında bir eşleme kurulmuştur denir.
E7. Birbirine eş olan iki üçgende karşılıklı taban açıları birbirine eştirler.
şeklinde bir belit tüm dertlere derman olur. Anlatmak istediği şudur:
b  b'


 m( B )  m( B ') 




c

c
'
ise


 m(C )  m(C ')  .
 m( A)  m( A ') 


a  a'




Bu eşleme
ABC  ABC
yazarak gösterilir. Böyle bir eşlemede kenar uzunlukları ve
açı ölçüleri de eşlenmiş olur. Bu eşlemeler de benzer olarak
a  a
b  b
c  c
m(A)  m(A)
m(B)  m(B)
m(C)  m(C)
şeklinde gösterilirler.
Üçgenlerde eşliğin yukarda verdiğimiz tanımı, iki kenar ve
bunların belirttiği açıdan bahsettiğinden bu tanıma K.A.K.
(Kenar-Açı-Kenar) tanımı denir.
Örnek. Birbirlerine paralel
A
olmayan [AC] ve [BD] doğru
parçaları birbirlerinin orta
noktalarından şekildeki gibi
E noktasında kesişiyor olsun- B
lar. Buna göre aşağıdaki ifadelerden hangisi doğru olmayabilir?
Tanım. Aralarında ABC  ABC gibi bir eşleme kurulmuş
olan iki üçgende, karşılıklı (eşleştirilmiş) kenarlar ve karşılıklı açılar eş ise bu iki üçgene eş üçgenler denir.
D
E
C
A) AB // DC
B) AD // BC
C) [AB]  [CD]
D) [AD]  [BC]
E) [AC]  [BD]
Kenarların eşliğinin aynı uzunlukta olmaları, açıların eşliğinin de aynı ölçüye sahip olmaları olduğunu hatırlatırız.
Çözüm: [AB], [BC], [CD] ve
A
D
[DA] hakkında bilgiler istendiğinden önce bu doğru parE
çalarını çizelim. Evvela AEB
ile CED üçgenlerini masaya B
C
yatıralım. Bu iki üçgende de
ortak boyda iki kenar var olup bu kenarların belirttiği açı ölçüleri de ters açılar gereği eş olduğundan yani |AE| = |CE| ve
|BE| = |DE| olup m(AEB) = m(CED) olduğundan K.A.K. tanımı gereği AEB ile CED üçgenleri eştir. Bu eşlik hem [AB]
 [CD] olmasını hem de m(A) = m(C) ve m(B) = m(D) olması doğurur. Doğan ilk eşitlik ise C şıkkının, diğer iki eşitlikse
A şıkkının doğruluğunu garantiler.
Yani
a = a
b = b
c = c
m(A) = m(A)
m(B) = m(B)
m(C) = m(C)
olmalı. Aslında karşılıklı kenarların ikisi eşit boydayken, bu
kenarların belirttiği açı ölçüsü de eşitse, diğer eşitlikler zaten
olmak zorundadır, hepsini incelemeye gerek yoktur. Niye
diye sorarsanız kanıtlayamayacağımız için, birazdan bir aksiyom vererek bu durumu tartışılmaz hale getireceğiz. Neyse, eğer böyleyse, bu üçgenlerin eşliği
ABC  ABC
yazılarak gösterilir. Ama ben yine, affınıza sığınarak,
ABC  ABC
diye göstereceğim, siz de anlayacaksınız.
Şimdiyse AED ile CEB üçA
D
genlerine odaklanalım. Bu
iki üçgende de |AE| = |CE| ve
E
|BE| = |DE| olup m(AED) =
m(CEB) olduğundan K.A.K. B
C
tanımı gereği AED ile CEB
üçgenleri eştir. Bu eşlik hem [AD]  [BC] olmasını hem de
m(A) = m(C) ve m(B) = m(D) olması doğurur. Doğan ilk
eşitlik ise D şıkkının, diğer iki eşitlikse B şıkkının doğruluğunu garantiler. O halde yanlış olan seçenek E seçeneğidir.
Bunu da kısaca izah edelim: Doğru parçalarının eş olması,
2
boylarının birbirlerine eşit olmasıyla mümkündü. Burada
[AC] ile [BD] keyfi olarak seçilen iki doğru parçası olduğundan daima eşit boyda olmaları beklenemez.
Doğru cevap: E.
Yukarda resmedilen iki üçgen eştir denilebilir mi? Yani,
karşılıklı iki kenar uzunluğuyla, bunların belirttiği değil de
diğer karşılıklı açılardan herhangi birinin ölçüsü eşit olsa
üçgenler yine eştir diyebilir miyiz? Hem sorunun kendisi
çok hoş, hem de cevabı. Olmazsa olmaz bu soruyu ve cevabını lütfen tam anlamıyla idrak edin.
Üçgende eşliğin K.A.K. tanımı ilerde sıkça kullanacağımız
şu çok önemli teoremi de kanıtlar:
Teorem. Açıortay doğrusu üzerinde alınan rastgele bir noktanın açının kollarına olan uzaklıkları eşittir.
Kanıt: Açımız yan şekildeki gibi
B
CAB açısı, bu açının açıortayı üzeP
rinde rastgele alınan nokta P ve


P’den açının kollarına inilen dikme
A
C
ayakları da B ve C olsun. PBA ile
PCA üçgenlerinde [AP] kenarı ortak
ve |AB| = |AC| olup A açıları da eş diye K.A.K. eşliği gereğince PBA ile PCA üçgenleri eştir. Dolayısıyla |PB| = |PC|
dir.
Sorunun cevabı tabii ki, ‘’hayır’’. Nedeni basit. Anlatayım:
Bir d doğrusu ve bu doğruya uzaklığı 3 birim olan bir P noktası düşünün. Doğru üzerinde bu noktaya 4 birim uzaklıkta
bulunan kaç nokta vardır? P noktasını merkez kabul eden 4
birim yarıçaplı bir çember çizilirse,
P
bu çember doğruyu şekilde gösterildiği gibi Q ve Q gibi iki farklı
4
3 4
noktada keseceğinden, “Tabii ki 2”
d
denir. Dolayısıyla BC üstünde |AC|
Q
Q'
= |AC = |AC olacak şekilde bir
C noktası daha olabilir. Bu yüzden bu eşlikten her zaman
bahsedilemez. “Her zaman” dedik, çünkü bazen bahsedilebilir. Örneğin, noktanın doğruya uzaklığı 3 birim ise doğru
üzerinde bu noktaya uzaklığı 3 birim olan tek bir nokta olabileceğinden yani farklı bir C noktası bulunamayacağından
bu üçgenler eş olur. Yani o noktadan doğruya istenilen
uzunlukta doğru parçası çizildiği zaman, doğruyu ne tür bir
açıyla kestiğini bilmemiz lazımmış. Bunu aşağıdaki teoremde vereceğiz.
Problem. ABC bir üçgen
|AB| = |DC|
m(BCA) = 
m(CAD) = 
3+ 2= 180
olduğuna göre α =  = 36 olduğunu gösteriniz.
Çözüm: Yan şekildeki gibi ABE ikizkenar üçgeni
oluşturulsun. EAC üçgeni
de ikizkenar olur. Buradan
AEB ile ACD üçgenlerinin
eşliği görülür. (K.A.K.).
O halde m(EAB) = m(ACD) = = = 36.
Tanımda geçen ‘’türdeş’’ kelimesinin ne anlama geldiğini
bilmeyenler olabilir, hemen bir tanım verelim:
İki açının ölçülerinin her ikisi de dar, her ikisi de dik veya
her ikisi de genişse, yani aynı tür açıysa, bu açılara türdeş
açı denir.
K.K.A.AT Eşlik Teoremi. İki üçgen arasında K.K.A. durumu varsa ve ayrıca üçüncü kenarlara ait açılar türdeş ise
üçgenler birbirine eştir.
Problem. ABC bir üçgen
|AC| = |BD|
3+ 2= 180
olduğuna göre m(ABC)
aşağıdakilerden hangisine
eşittir?
A)
1
2
α
B) 15º + α
Kanıt: K.K.A. durumuna uyan üçgenler ABC ve ABC olsunlar. b = b, c = c, m(B) = m(B) olup, ayrıca m(C) ile
m(C) türdeş olsun. a a kabul edelim, örneğin a < a olsun.
C) 30º– α
D) α
E) 2α
Çözüm: [BD] üzerinde
DAE üçgenini ikizkenar yapacak şekilde bir E noktası
alalım. m(DAE) = α olacağından ACE üçgeni ikizkenar olur, o halde |AC| = |EC| dir. Buradan ADC ile AEB üçgenlerinin eşliği görülür (K.A.K.), demek ki |AC| = |AB|.
Doğru cevap: D.
[BC üzerinde |BC = |BC olmak üzere C noktasını alalım. K.A.K. tanımından ABC  ABC olur ve bundan dolayı |AC = |AC olup ACC üçgeni ikizkenar olur. C''
noktası, B ve C noktaları arasında olduğundan m(C) = 90o ve
m(C) = 90o olamaz. Bu durumda ACC üçgeninde m(C) dış
açı ölçüsü m(C) iç açı ölçüsünden büyük olur. m(C) ile
m(C)nün türdeş olmadığı gösterilmiş olur ki bu sayıltıya
(kabulümüze) aykırıdır.
Eşliğin K.A.K. tanımında A harfinin K harflerinin arasına
yazılması simetrik görünsün diye değildir. Yani K.K.A. veya
A.K.K. deme hakkına sahip değiliz. Peki, uygun koşullar altında böyle eşlikler de var mıdır? Şekil çizelim:
3
a > a durumunda da benzer bir çelişki çıkar. Dolayısıyla a
= a olursa bu üçgenler eştir.
eşitlik b = b veya c = c. Çünkü bundan sonrasını üçgenin
K.A.K. tanımına göre halledebiliriz.
Örnek. Şekildeki ABC açısıA
nın açıortayı [BD dir.

D
|DA| = |DC|
m(BCD) = 70º
70o
m(DAB) = α
B
C
olduğuna göre α’nın derece
cinsinden alabileceği en küçük tam sayı değeri kaçtır?
A) 70
B) 80
C) 90
D) 110
|BA = c  c farz ederek BA üstünde |BA = c br olacak
şekilde bir A noktası alalım. K.A.K. tanımından ABC ile
ABC üçgenleri eştir. O halde
m(BCA) = m(BCA) = m(BCA)
bulunur ki; A ile A noktalarının BC kenarının aynı tarafında olmaları nedeniyle, E1 aksiyomu gereğince
A = A yani c = c.
E) 140
Çözüm: ABD ile CBD üçK
genlerinin iki kenarı ve bir iç
A 70o k
açısı eş diye bu üçgenlere eş

D
k
demeyin sakın. K.K.A. duk
rumunun bazen eşliğe yet70o
mediğini yukarda açıkladık.
B
C
[BA üzerindeki bir K noktası
için ADK ikizkenar üçgenini oluşturalım. |DC| = |DA| = |DK|
= k br olsun. BKD açısının dar, BAD açısının geniş olduğuna
dikkat ediniz. Yani BCD açısıyla türdeş olan BKD açısıdır.
Bu yüzden eş olan üçgenler BKD ile BCD üçgenleridir. Demek ki α’nın 70º olma durumu da var 100º olma durumu da
var. Küçük olan 70 değeri cevap olacak.
Doğru cevap: A.
Örnek. ABC bir üçgen
A
|CA| = 5 br

|AB| = 3 br


|BD| = 2 br

m(DAB) = θ

C
B
D
m(ABC) = 2α
3α + 2θ = 180º
olduğuna göre m(BCA) aşağıdakilerden hangisidir?
A) α
B) 2α
C) θ
D) 2θ
Teorem. Bir paralelkenarın karşılıklı kenar uzunlukları birbirlerine eşittir.
Kanıt: Paralelkenarımız
A
D

yandaki ABCD paralelke
narı olsun. AD // BC diye
m(BDA) = α dersek


m(DBC) = α ve AB // DC
B
C
diye m(ABD) =  dersek
m(CDB) =  olur. ABD ve CDB üçgenlerinin ikişer açısı
karşılıklı olarak eş iken bu açıların ortak olan kolları iki üçgende de eşit boyda olduğundan ADB ile CDB üçgenleri
A.K.A. eşliği gereğince eştirler. Bu yüzden karşılıklı kenarları da eş olmalıdır.
K.K.K. Eşlik Teoremi. Kenarları karşılıklı eş olan iki üçgen eştir.
E) θ – α
Çözüm: Sorunun esprisi 2 + 3
A
= 5 olmasıdır. Bu amaçla [AB]

kenarını B yönünde 2 br uzata

rak DBE ikizkenar üçgenini
  
oluşturalım. Bu üçgende B’ye
B   D
C
ait dış açı ölçüsü 2α olduğun 
dan B ve D açılarının ölçüleri
α olur. ABD üçgeninde iç açı- E
ların ölçüleri toplamından
m(BDA) = α + θ ve dış açı teoreminden m(ADC) = 2α + θ
olur. Şimdi CAD ile EAD üçgenlerine odaklanalım. K.K.A.
durumu halihazırda var. O zaman bu üçgenlerde C ve E açıları türdeşse eşlikten bahsedebiliriz. 2α + θ geniş olduğundan hem E hem de C açısı dardır yani türdeştirler. O zaman
bu eşlikten dolayı m(BCA) = α olur.
Doğru cevap: A.
Kanıt: a = a, b = b, c = c durumunda herhangi bir karşılıklı açının eşliğini göstermek yetecek. Kalanı yine K.A.K. tanımı halledecek. BC kenarının A noktasının bulunmadığı tarafında m(CBA) = m(CBA) ve |BA = |BA olacak şekilde bir A noktası alalım. K.A.K. tanımı gereği ABC ile
ABC üçgenleri eştir. O halde |AC| = |AC = b br olur.
Yine K.A.K. tanımından b = b olduğundan ABC ile ABC
eş bulunur ki b ve b uzunluğundaki kenarların karşılarındaki
açı ölçüleri eşit olmalıdır.
Sonuç. Karşılıklı kenar uzunlukları birbirlerine eşit olan bir
dörtgen paralelkenardır.
Dörtgenimiz |AD| = |BC|
A
D

ve |AB| = |CD| olmak üze

re ABCD dörtgeni olsun.
Derhal [BC] köşegenini



çizelim. ABD ile CDB üçB
C
genlerinin kenar uzunlukların karşılıklı olarak birbirlerine eşit uzunlukta olduğunu
A.K.A. Eşlik Teoremi. Tabanları ve karşılıklı taban açıları
eş olan iki üçgen birbirine eştir.
Kanıt: ABC ve ABC gibi iki üçgende a = a, m(B) = m(B)
ve m(C) = m(C) olsun. Doğruluğunu göstermek istediğimiz
4
fark ettiniz mi? İşte bu yüzden bu üçgenler K.K.K. eşliği gereği birbirlerine eştirler. O halde m(BDA) = α dersek
m(DBC) = α ve m(ABD) =  dersek m(CDB) =  olur. Bu da
iç ters açıların karşıtı gereği AD // BC ve AB // CD demektir.
Çözüm: Burada ilk
A 
dikkat edilmesi gereF
ken nokta ABC üçgeninin B ve C açılarıD


nın eşit ölçülü olma

30
larından dolayı ABC
B
C
E
üçgeninin ikizkenar
olmasıdır. Her ikizkenar üçgende yapılması gerektiği gibi
evvela A’dan BC’ye bir dik indireceğiz. Dikme ayağına E
diyelim. CD’nin AE’yi kestiği nokta F olsun. [BF]’yi de çizelim. AE  BC ve |BE| = |EC| olması FBC üçgeninin de
ikizkenar olmasını gerektirir. O halde m(FBD) = α, dolayısıyla m(ABF) = α olacaktır. Şimdi BAF ve BDF açılarının
ölçülerinin 60º – α olduğunu görüp [BF] ortak kenarından
dolayı BAF ile BDF üçgenleri A.K.A. veya K.A.A. eşliği gereğince eştirler. Bu eşlikten dolayı ABD üçgeni ikizkenar bulunur ki tepe açısının ölçüsü 2α olduğundan taban ölçüleri
90º – α olmalıdır. Buradan m(FAD) = 30º, dolayısıyla
m(DAC) = 30º – α olarak bulunur.
o
o
Örnek. ABC bir üçgen
|BD| = |DC|
|AD| = |BC|
m(DBC) = m(DCB) = 
m(ADB) = 60 + 
olduğuna göre olduğunu
gösteriniz.
Çözümü: Yan şekildeki
gibi BCDE paralelkenarını
oluşturalım. m(BDE) = α
olacağından m(EDA) = 60
olur. |BC| = |ED| = |DA| olduğundan ADE bir eşkenar
üçgendir. Diğer yandan
AEB ile ADB üçgenleri
K.K.K. eşliği gereğince eş olduklarından = 30o bulunur.
Teorem. Bir üçgenin herhangi bir kenarının orta noktasından üçgenin ikinci kenarına
paralel olacak şekilde geçen
doğru, üçgenin üçüncü kenarının orta noktasından geçer.
A'
c'
a
C B'
C'
a'
Kanıt: a = a, m(A) = m(A) ve m(B) = m(B) kabul edebiliriz. c > c olduğunu farz ederek, [BA üzerinde |BA = |BA
olacak şekilde A noktası alalım. ABC ile ABC üçgenleri
K.A.K. eşliği gereği eş olduğundan m(A) = m(A) olmalıdır.
Fakat, CAA üçgeninde dış açı teoremi uygulandığında
m(CAB) = m(CAA) + m(ACA) > m(A) = m(A) bulunur ki
bu bir çelişkidir. Öyle ise A = A olup c = c olur. c < c kabul edilseydi de benzer bir çelişki bizi karşılardı. Bu da iki
üçgenin eşliğini kanıtlar.
Örnek. ABC bir üçgen
D  (ABC)
m(ABD) = 2α
m(DBC) = 30º – α
m(BCD) = 30º


m(DCA) = α
B
olduğuna göre
m(CAD) = 30º– α olduğunu gösteriniz.
o
E
D
B
C
Kanıt: DE // BC olduğundan
A
yöndeş açıların eşliği gereğince ADE ile ABC ve DEA ile

 E
D
BCA açıları eş olurlar.
m(ADE) = m(ABC) =  ve



m(DEA) = m(BCA) =  diyeB
C
F
lim. Şimdi E’den AB doğrusuna bir paralel çizelim. Bu doğru BC’yi F’de kessin. BFED
dörtgeninin karşılıklı kenarları birbirlerine paralel olduğundan yani bir paralelkenar olduğundan daha önce kanıtladığımız üzere karşılıklı kenarları eş olur. O halde |AD| = |DB|
= |EF| eşitliğinden bahsedilebilir. Diğer yandan EF // AB olduğundan EFC açısının ölçüsü de  olur. Bu da ADE ile
EFC üçgenlerinin K.A.A.eşliği gereğince eş olduklarını işaret eder. Bu eşlik aradığımız |AE| = |EC| eşitliğine yeter de
artar bile.
A''
B
A
Yani şekle göre DE // BC ve |AD| = |DB| ise |AE| = |EC| dir.
K.A.A Eşlik Teoremi. İkişer açısı ve karşılıklı birer kenarı
eş olan iki üçgen birbirine eştir.
c' A
c
o
Yukardaki [DE] doğru parçası gibi, bir üçgenin herhangi iki
kenarının orta noktalarını birleştiren doğru parçalarına orta
taban denir.
A
D
Orta taban şekilden de görüleceği üzere daima tabana paraleldir. Diğer yandan ADE ile EFC üçgenlerinin eşliği |DE| =
|BF| = |FC| eşitliğini doğuracağından orta tabanın boyunun
tabanın boyunun yarısı olduğunu anlarız.

30o
C
Sonuç: Bir üçgenin üç tane
orta tabanı vardır. Bu orta tabanların belirttiği üçgene asıl
üçgenin orta üçgeni denir.
Orta üçgenin kenarlarının asıl
üçgene paralel olduğuna ve
5
A

D

B




 E
 
 
F

C
kenarlarının asıl üçgenin kenarlarının yarısı kadar olduğuna
dikkat ediniz. Bunun yanında ADE, DBF, EFC ve FED üçgenlerinin eş olması da kayda değer bir durumdur.
Örnek. ABCD bir dörtgen
DA  AB
|BE| = |EC|
m(BDA) = m(FDA)
|BD| = 10 br
|CD| = 8 br
olduğuna göre |AE| = x kaç br
dir?
F
A
x 10
Problem E1. ABC bir üçgen
CDA ve AEB birer eşkenar
üçgen
BD  CE = {P}
BD
olduğuna göre
= 1 olCE
D
8
E
B
ÇÖZÜMLÜ PROBLEMLER
A
E
P
C
B
duğunu gösteriniz.
C
Çözüm: CDA ve AEB birer
D
eşkenar üçgen olduklarından
A
m(DAC) = m(BAE) = 60
60
60 
olmalıdır. m(CAB) = α olsun. E
P
Şimdi CAE ve DAB üçgenlerine
odaklanıyoruz.
C
B
|AE| = |AB|, |CA| = |DA| ve
m(CAE) = m(DAB) = 60 + α olduğundan CAE ve DAB üçgenleri eştir. Bu yüzden |CE| = |BD| olmalıdır. Dolayısıyla
da oranları 1’dir.
Çözüm: Ne zaman orta nokta
K
görürseniz aklınıza ilk olarak
orta taban gelsin demiştik. Şe10
kilde orta taban olmaya aday tek
doğru parçası |BE| = |EC| olduD
A
ğundan [AE] dir. Bu amaçla
[CD]’yi D yönünde uzatalım.
8
x 10
CD ile BA’nın kesim noktası K
olsun. Şimdi BDK üçgenine
C
E
B
odaklanıyoruz. Bu üçgende
[DA] hem iç açıortay hem de yükseklik olduğundan BDK
ikizkenar üçgendir. O halde [DA] aynı zamanda kenarortaydır. |BD| = 10 br olduğundan |DK| = 10 br olacağını da not
edelim. Sona geldik. |CK| = 8 br + 10 br = 18 br olduğundan
|AE| = 9 br olmalıdır.
Örnek. ABC bir dik üçgen
AB  BC
BE  AD
|BD| = |CD|
m(BAD) = 2∙m(DAC) = 2α
|DE| = 3 br
olduğuna göre
|AB| = x kaç br dir?
D
o
o
Bu eşliğin oluşması için sadece eşkenar üçgen değil, diğer
düzgün çokgenlerin yapıştırılması da yeter!
A
 
x
E
3
B
D
C
Problem E2. ABC bir üçgen CDA ve AEB birer eşkenar üçgen
BD  CE = {P}
m(CPB) = 
olduğuna göre  = 1200 olduğunu gösteriniz.
Çözüm: C’den BE’ye indiA
6
rilen dikme ayağı F olsun.
F

 
DE // CF olup |BD| = |DC|
olması BCF üçgeninde
E
6
6
[DE]’nin orta taban olması
3

anlamına gelir. O halde
|DE| = 3 br olduğundan
B
C
D
|CF| = 6 br olur. Şimdi A
ile F noktalarını birleştirelim. [ED] orta taban olduğundan
|BE| = |EF| olduğunu biliyoruz. FAB üçgeninde [AE] hem
kenarortay hem de yükseklik olduğundan FAB ikizkenar üçgen olup [AE] aynı zamanda iç açıortaydır. Bu yüzden
m(CAF) = α olmalıdır. Diğer yandan AD // FC olduğundan
iç ters açıların eşliği gereği ACF açısının ölçüsü de α olur.
Sonuç olarak CFA üçgeni de ikizkenar bulunur. O halde |CF|
= |FA| = |AB| = 6 br olmalıdır.
D
A
E
P

C
B
Çözüm: Lafı uzatmayalım.
D
Bir önceki soruda CAE ve

A
DAB üçgenlerinin eş olduk60
larını kanıtlamıştık. CAE üç- E  60 
P
geninin C ve E açılarının öl

120
çülerine sırasıyla  ve  derC
B
sek DAB üçgeninin D ve B
açılarının ölçüleri sırasıyla 
ve  olmalıdır. Bu üçgenlerin herhangi birinin iç açılarının
ölçüleri toplanırsa α +  +  = 120 bulunur. Bu toplam
o
o
o
6
CABP konkav dörtgeninde kullanılırsa m(CPB) =  = 120
bulunur.
AF
FB

BD
DC

CE
EA
olduğuna göre FDE üçgeninin
eşkenar olduğunu gösteriniz.
Boyları eşit olan doğru parçalarının 120 yani 60 ile kesişmeleri bir rastlantı değildir.


α = 60
α = 90
Çözümü: |AF| = |BD| = |CE| = x
A
br ve |FB| = |DC| = |EA| = y br oly
60o
sun. FBD, DCE ve EAF üçgenleE
x
rinin ikişer kenar uzunluğu ve bu
z
kenarların belirttiği açılar da eş
x
F
z
olduğundan FBD, DCE ve EAF
y o z
60
60o
üçgenleri eştir. O halde |FD| = z
x
D y C
br dersek |DE| = |EF| = z br olur. B
DEF üçgeninin üç kenar uzunluğu da birbirlerine eşit olduğundan DEF eşkenar üçgendir.

α = 108
ABC üçgeninin kenarlarına hangi tip düzgün çokgen yapıştırılmışsa o düzgün çokgenin bir iç açısının ölçüsüyle kesişirler!
Problem E3. ABC ve ADE birer eşkenar üçgen
|BD| = x br
|CE| = y br
olduğuna göre x = y olduğunu gösteriniz.
Ortadaki şeklin eşkenar üçgen çıkması, ABC üçgeninin eşkenar üçgen verilmesindendi.
A
E
x
y
D
B
60o
108o
C
Eğer ilk şekil eşkenar üçgen yerine herhangi bir düzgün
çokgen olsaydı ortadaki şekil de o düzgün çokgenin bir yavrusu olurdu!
Çözüm: ABC ve ADE üçgenleri eşA
kenar olduklarından |AB| = |AC|
ve |AD| = |AE| olduğunu biliyoruz.
  
m(BAD) = α ve m(DAC) = θ dersek
E
α + θ = 60º olduğundan m(CAE) = α
y
D
olur. Bu da K.A.K. gereği BAD ile
x
CAE üçgenlerinin eş olması anlamıB
C
na gelir. Madem eşler, eş açıları
gördükleri kenarların boyları da eşit olmalıdır. O halde x =
y’dir.
Problem E5. ABC eşkenar üçgen
D  [BC]
E  [CA]
|BD| = |CE|
|DC| = |EA|
AD  BE = {K}
olduğuna göre
m(DKB) = 600 olduğunu gösteriniz. B
A
E
K

C
D
Bu eşlik sadece eşkenar üçgenlere has değildir.
Çözüm: |BD| = |CE| = x br ve
|DC| = |EA| = y br olsun. |AB| = x
+ y br olur. Şu durumda ABD ile
BCE üçgenlerine bakılırsa ikişer
x+y
kenarları eşit uzunluktayken bu
kenarların belirttiği açıları da eş

diye K.A.K. gereği ABD ile BCE

x
eş olurlar. m(DAB) =  denirse B
m(EBC) =  olur. m(ABE) =  olsun.  +  = 60 olduğundan ABK üçgeninin
toplanırsa α = 60 olarak bulunur.
Aynı kenar sayısına sahip iki düzgün çokgenin bir köşesi ortaksa daima böyle eşlikler belirir.
Problem E4. ABC bir eşkenar üçgen
F  [AB]
D  [BC]
E  [CA]
A
E
F
B
7
D
C
A
y

E
K

x
D
60o
y
C
iç açı ölçüleri
Problem E7. ABC bir eşkenar üçgen
F  [AB]
D  [BC]
E  [CA]
|FA| = |DC|
F
|BD| = |CE|
olduğuna göre m(FDE) = 600 oldu
B
ğunu gösteriniz.
Cevabın 60 çıkması ABC üçgeninin eşkenar olmasındandır.
90o
o
o
60
108
A
E

C
D
Eşkenar üçgen yerine başka bir düzgün çokgende aynı durum olsaydı, cevap o düzgün çokgenin bir iç açısının ölçüsü
olurdu!
Problem E6. ABC bir eşkenar üçgen
F  [AB]
D  [BC]
E  [CA]
AF
BD
CE


FB
DC
EA
olduğuna göre KLM üçgenin
eşkenar olduğunu gösteriniz.
Çözüm: ABD ile BCE üçgenleri
eştir. O halde m(BAD) = m(CBE)
olduğundan m(ABM) =
m(BCK)’dır. Dolayısıyla m(LKM)
= 60o bulunur. Simetrik şekilde
diğer benzerliklerden de faydalanarak m(KLM) = 60o bulunur.
Dolayısıyla KLM üçgeni eşkenardır.
Çözüm: |BD| = |CE| = x br ve
A
|FB| = |DC| = y br olsun. FBD ile
DCE üçgenlerinin ikişer kenar
E
uzunluğu ve bu kenarların belirt
tiği açılar da eş olduğundan FBD
x
F
ile DCE üçgenleri eştir. FBD üçy o

geninde F ve D açılarının ölçüleri
60
 60o

x
D y C
 ve  dersek, DCE üçgeninde de B
D ve E açılarının ölçüleri  ve 
olur.  +  = 120 olduğundan α = 60 olarak bulunur.
A
E
K
F
M
L
B
D
C
60 burada rastgele bir değer değil, eşkenar üçgenin bir iç
açısının ölçüsüdür.
A
K
F
L
B
60o
60o o
60
60o
E
108o
Aynı durum karede olsa cevap 90, düzgün beşgende olsa
108 olurdu.
M
D
90o
C
Problem E8. ABC bir eşkenar üçgen
D iç bölgede bir nokta
|DA| = x br
|DB| = y br
|DC| = z br
x2 + z2 = y2
olduğuna göre
m(ADC) =1500 olduğunu gösteriniz. B
Ortadaki şeklin eşkenar üçgen çıkması, ABC üçgeninin eşkenar üçgen olmasına bağlıdır.
Eğer eşkenar üçgen yerine başka bir düzgün çokgende aynı
işlemler yapılırsa, ortada düzgün çokgenin yavrusu oluşur!
A
x
D
y
z
C
Çözüm: [AD] kenarı üzerine üçA
x
genin dışına doğru şekildeki gibi
E
bir eşkenar üçgen çizelim.
x
60 x
m(BAD) = m(CAE), |AB| = |AC|
D
y
ve |AD| = |AE| olduğundan BAD
z
y
ile CAE eş olur. O halde |EC| = y
br olur. EDC üçgeninin kenarları
B
C
x br, z br ve y br olup Pisagor Teoremi’ni sağladığı görülürse
m(EDC) = 90o olduğu anlaşılır. Dolayısıyla
m(ADC) = m(ADE) + m(EDC) = 60o + 90o = 150o bulunur.
Hepsinde de maviyle gösterilmiş doğru parçalarının boyları
eşittir.
8
Problem E9. ABC bir eşkenar üçgen
D iç bölgede bir nokta
|DA| = x br
|DB| = y br
|DC| = z br
y2 = x2 + z2  xz
olduğuna göre
m(ADC) = 1200 olduğunu gösteriniz. B
Problem E11. ABC bir eşkenar
üçgen C dışarıda bir nokta
m(BCA) = m(ACD) = 60º
|CB| = x br
|CD| = y br
|CA| = z br
olduğuna göre z = x + y olduğunu
gösteriniz.
A
x
D
y
z
C
A
z
B
D
o
60o 60 y
x
C
Çözümü: [AD] kenarı üzerine
A
üçgenin dışına doğru şekildeki
x
gibi bir eşkenar üçgen çizelim.
x
E
m(BAD) = m(CAE), |AB| = |AC|
o
60 x
D 60o
ve |AD| = |AE| olduğundan BAD
y
ile CAE eş olur. O halde |EC| = y
y
z
br olur. Şimdi EDC üçgeninin
B
C
kenarları x br, z br ve y br olduğuna dikkat ediniz. Kosinüs teoremi gereği y2 = x2 + z2 – 2xz cos(EDC) olmalıdır. Soruda bu
değer y2 = x2 + z2  xz olarak verildiğinden
2xz cos(EDC) = xz
olmalıdır ki buradan cos(EDC) = 1/2 çıktığından
m(EDC) = 60º
olduğu anlaşılır. Şu durumda
m(ADC) = m(ADE) + m(EDC) = 60o + 60o = 120o
bulunur.
Çözümü: m(ADC) > 60º olduğunA
dan [AC] üzerinde m(CDE) = 60º
olacak şekilde bir E noktası alınabilir. CDE eşkenar üçgen olur.
x
Şimdi BCD ile AED üçgenlerine
120o
odaklanıyoruz.
y
E
|BD| = |AD| ve |CD| = |ED| olduğuB
 D
y
nu biliyoruz. m(CDB) = α dersek,
y
x
m(EDA) = α olacağından BCD ile
o
o
C
60
60
AED üçgenleri eştir. Bu durumda
|BC| = x br olduğundan |AE| de x br olmalıdır. O halde
|AC| = z = |CE| + |EA| = y + x br olarak bulunur.
Problem E12. Dar açılı ABC üçgeninin diklik merkezi H
olup AH = BC ise m(BAC) = ?
A
Problem E10. ABC bir eşkenar üçgen
A, C, D doğrusal
|BE| = |CD|
m(BAE) = 
m(CED) = α
olduğuna göre α =  olduğunu
gösteriniz
B
Çözüm: m(HAE) = m(HBD),
m(BCE) = m(AHE) ve AH = BC
olduğundan AHE ve BCE üçgenleri A.K.A’dan eş olup AE = BE
olur. Bu durumda ABE ikizkenar
dik üçgen olup m(BCA) = 450 =
m(BAC) = 450 olacaktır.
A

E

H
B
E
C
D
C
D
Problem. ABC üçgeninde AH yükseklik olup BC, CA, AB
kenarlarının orta noktaları sırasıyla D, E, F ise FHE 
FDE olduğunu gösteriniz.
Çözüm: E’den BA’ya paralel çiA
zilen doğru CA’yı K’de kessin.
x
AB // EK diye m(AEK) =  ve
K

KEC eşkenar üçgen olur.
y
AED üçgeninin bir önceki soru
 y
tipi olduğunu fark ettiniz mi?
y
C
|EC| = |CK| = |KE| = y br ve

B x E
x
|BE| = |CD| = |KA| = x br olsun.
D
m(ECD) = m(EKA) = 120
olduğunu da görelim.
Şu durumda ECD ile EKA eş olurlar. O halde α =  olmalıdır.
A
Çözüm: ABC üçgeninde D, E, F
kenar orta noktalar olduğundan
2.FE = BC, 2.FD = AC ve 2.DE
= AB dir. ABH dik üçgeninde AF
= FB= FH ve ACH dik üçgeninde AE = EC = EH olur. Bu durumda FHE ve FDE üçgenleri
K.K.K’dan eştir.
9
F
B
E
D
H
C
Problem. ABC dik üçgeninde AC ve BC kenarları üzerinde
sırasıyla alınan K ve L noktaları için BK = KL dir. m(BAC) =
900 ve m(BCA) = m(ABK) = 180 ise LC = 2.AB olduğunu
gösteriniz.
C
Çözüm: m(CAP) =
m(PCX) = α olsun.
Bu
durumda
m(YAM) = m(XCM)
P
= 450 - α’dır. CX =
Y
X
AY ve AM = CM olB
A
//
duğundan YAM 
M
XCM olur. Dolayısı
ile YM = XM ve m(YMA) = m(XMC) olur. CM  AB olduğundan m(YMX) = 900 dir.
B
L
18
18
N
18
A
K
M
C
Çözüm: Verilenlere göre m(LKC) = 360 olup KC üzerinde
KL = ML olacak şekilde bir M noktası alalım. M’den LC’ye
inilen dikme ayağı N olsun. Bu durumda LN = NC olacaktır.
BK = MC ve m(BCA) = m(ABK) = 180 olduğundan
A.K.A’dan ABK  NCM olup NC = AB olur. Dolayısı ile
LC = 2.AB dir.
Problem. ABC ikizkenar dik üçgenininde m(B) = 900 olup
AB ve BC kenarları üzerinde sırasıyla P ve Q noktaları alınsın. BP = BQ olmak üzere P ve B’den geçen AQ’ya dik doğrular AC’yi sırasıyla K ve L’de kessin. KL = LC olduğunu
gösteriniz.
Problem. ABC üçgeninin AC ve AB kenarları üzerine dışa
doğru ACB1 ve ABC1 ikizkenar dik üçgenleri inşa edilsin.
BC’nin orta noktası D olmak üzere DC1 = DB1 ve DC1 
DB1 olduğunu gösteriniz.
Çözüm: AB’nin uzantısı
üzerinde PB = BR olacak
şekilde bir R noktası alalım.
Ayrıca
AQ  RC  S olsun. BR
= BQ ve BC = AB olduğundan  ABQ CBR
olur. Bu durumda AS 
RC olup PK // BL // RC
olacaktır. BP = BR olduğundan KL = LC’dir.
Çözüm: AB ve AC’nin orta noktası sırasıyla E ve F olsun.
AB
AC
Bu durumda EC1 
 FD ve FB1 
 ED olup
2
2
A
m(DEC1)
=
m(DFB1) dür.
Bu
durumda C1
DEC1 ve B1FD
E
F
üçgenleri
eş
olup DC1 = DB1
dür. Üçgenlerin
eş olmasından
C
B
faydalanarak
D
açıları
yerine
yazdığımızda DC1  DB1 olduğu da ortaya çıkar.
A
K
P
L
Q
B
C
S
R
B1
Problem. ABC ikizkenar dik üçgen olup BA  CA’dır. AB
kenarının orta noktası M olmak üzere A’dan geçen CM’ye
dik doğru BC’yi N’de kessin. Bu durumda m(AMC) =
m(BMN) olduğunu gösteriniz.
Çözüm: ABDC karesini
inşa edelim. AN, BD’yi
P’de kessin. MAC 
PBA olacağından PB =
AM = MB olur. Bu durumda BNM ve BNP üçgenleri eş olup m(BPN) =
m(BMN) olur. MAC 
PBA eşliğinden m(BPA)
= m(AMC) olup m(AMC)
= m(BMN) olur.
Problem. ABC ikizkenar dik üçgeninde m(C) = 900’dir. BC
üzerinde bir P noktası alınsın. [AP] üzerinde alınan X ve Y
noktaları için CX  AP ve AY = CX olsun. AB’nin orta
noktası M ise YMX üçgeninin ikizkenar dik üçgen olduğunu
gösteriniz.
10
A
C
M
N
B
//
P
D
Problem. ABC üçgeninde AD açıortay olup BC’ye D’de dik
olan doğru ile AB, E’de kesişsin. ED = CD ise BA  CA olduğunu gösteriniz.
Problem. ABC üçgeninin AB ve AC kenarları üzerine dışa
doğru ABDE ve ACFG kareleri inşa edilsin. Aşağıdaki ifadelerin doğruluğunu kanıtlayınız.
a.
b.
c.
E
Çözüm: D noktasından AB ve
AC’ye
inilen
A
R
dikme ayakları
Q
sırasıyla P ve Q
olsun. AD açıorP
tay olduğundan
DP = DQ’dur. B
C
ED = CD olduğu
D
göz önüne alınırsa  EPD CDQ olur. Bu durumda BA  CA olacaktır.
EC  GB dir.
EC, GB ve DF noktadaştır.
EG’nin orta noktası M olmak üzere MA  BC ve
BC = 2.MA’dır.
Çözüm:
a. P-E2’den EC  BG olur.
G
E
A
45
45
F
P
45
45
D
C
B
b. EC  GB  P olsun. EC  BG olduğundan ABDE ve
ACFG karelerinin çevrel çemberleri P’den geçer. Bu durumda m(CPF) = m(BPD) = 450 olduğundan D, P, F doğrusaldır.
Problem. ABCD karesinin AB kenarının orta noktası K ve
AC köşegeni üzerinde alınan bir L noktası için AL : LC = 3 :
1 ise m(KLD) = ?
Çözüm: AC = 4 alalım.
K ve D ve K’dan AC’ye
inilen dikme ayakları sırasıyla N ve M olsun. Bu
durumda AM = KM = 1,
AN = DN = 2 ve NL = 1
olur.
Dolaysı
ile
 LND  KML
olup
m(KLD) = 900 dir.
D
C
L
1
2
G
GG
11
M
1
E
E1
A
N
1
F
M
1
A
1
//
D
B
//
K
P
B H
C1
Problem. ABC üçgeninde AC < BC olup m(C)= 60 dir. BC
kenarı üzerinde alınan D noktası için BD = AC’dir AC kenarının uzantısı üzerinde alına bir E noktası için AC = CE ise
AB = DE olduğunu gösteriniz.
 AGG1  ACC1 olur. Bu durumda B1 = H = C1 olur. Bu
E
C
durumda BH = AE1 ve CH = AG1 olur. Bu iki eşitlik BC =
2.MA olduğunu gösterir.
Aynı şartlar altında A’dan geçen BC’ye dik doğrunun EG’yi
ortaladığını okuyucuya alıştırma olarak bırakalım.
// D
60
60
A
C
c. AM  BC  H olsun. E ve G noktalarından AM’ye inilen
dikme ayakları sırsıyla E1 ve G1 ve B ve C’den AH’a indirilen dikme ayakları sırasıyla B1 ve C1 olsun. EM = GM olduğundan EE1 = GG1’dir. Ayrıca  AEE1  ABB1 ve
0
Çözüm: BC kenarı üzerinde
alınan bir F noktası için BD
= CF olsun. Bu durumda
CD = BF olur. ADC eşkenar
olup EC = AF ve m(DCE) =
m(AFB) = 1200 olduğu göz
önüne alınırsa EDC ve AFB
üçgenleri eş olur. Bu durumda AB = ED’dir.
B1
F
//
B
ALIŞTIRMA PROBLEMLERİ
11
Alıştırma. AB doğru
parçası üzerinde bir C
noktası alınsın. AB’nin
aynı tarafında ACE ve
CBD eşkenar olacak
şekilde E ve D noktaları
verilsin. AD ile BE’nin
kesim noktası F olduğuna göre m(EFD) = ?
Alıştırma. ABCD karesinin A köşesinden CD
ve BC kenarlarını kesen
d1ve d2 doğruları çizilsin. Bu doğrulara BB1,
BB2, DD1, DD2 dikmeleri inilsin. Bu durumda
B1B2  D1D2 ve B1B2 =
D1D2 olduğunu gösteriniz.
Alıştırma. ABC eşkenar üçgeninin AB, BC, CA kenarları
üzerinde alınan X, Y, Z noktaları için XYZ üçgeni eşkenar olsun. A(ABC) = 2.A(XYZ) ise AX : XB =?
E
F D
A
B
C
Alıştırma. ABC üçgeninin CA ve CB kenarları üzerine dışa
doğru sırasıyla ACQ ve BCR dik üçgenleri inşa edilsin.
m(AQC) = m(BRC) = 900 ve m(CAQ) = m(CBR) olsun.
AB’nin orta noktası P ise PQ = PR ve m(QPR) = 2.m(CAQ)
olduğunu gösteriniz.
d2
D
Alıştırma.
Şekilde ARB, BPC,
CQA ikizkenar üçgenleri benzer olup
AR = BR, BP = CP
ve CQ = AQ’dur. Bu
durumda ARPQ’nun
paralelkenar olduğunu gösteriniz.
C
D2
B1
d1
B2
D2
A
B
A
Q
R
P
B
C
Alıştırma. ABCD karesinin DC kenarı üzerine dışa(veya
içe) doğru DCP üçgeni inşa edilsin. DP  CP, PC = 3 ve PD
= 4 ise PA = ?
Alıştırma. ABCD paralelkenar olup BC ve DC kenarları
üzerine dışa doğru BCQ ve DCP eşkenar üçgenleri inşa edilsin. AP = AQ olduğunu gösteriniz.
Alıştırma. ABCD karesinin DC kenarı üzerine dışa doğru
DCP üçgeni inşa edilsin. DP  CP olup DPC açısının açıortayı DC ve AB’yi sırasıyla K ve L de kessin. KC = AL olduğunu gösteriniz.
Alıştırma. ABCD konveks dörtgeninde AB ile DC, P’de, AD
ile BC, Q’da kesişsin. AB = PB = CQ ve DC = DQ ise
m(ABQ) = ?
Alıştırma. ABCD karesinin AD kenarı üzerinde P noktası ve
AB’nin uzantısı üzerinde Q noktası verilsin. DP = BQ ise
m(CPQ) = ?
Alıştırma. ABCD konveks dörtgeninde m(A) = m(B) = 1200
ve AD = BC’dir. DC kenarı üzerine dışa doğru PDC eşkenar
üçgeni inşa edilsin. APB üçgeninin eşkenar üçgen olduğunu
gösteriniz.
Alıştırma. ABCD karesinin AB, BC, CD, DA kenarları üzerinde sırasıyla A1, B1, C1, D1 noktaları verilsin. A1C1  B1D1
ise A1C1 = B1D1 olduğunu gösteriniz.
Alıştırma. ABC üçgeninin BC, CA, AB kenarları üzerinde sırasıyla A1, B1, C1 noktaları alınsın. AC1 = BA1 = CB1 olsun.
ABC ve A1B1C1 üçgenlerinin çevrel çemberlerinin merkezlerinin çakışık olması için gerek ve yeter şartın ABC’nin eşkenar olması gerektiğini kanıtlayınız.
Alıştırma. Dar açılı ABC üçgeninin diklik merkezi H olup
H’den geçen bir doğru AB ve BC’yi sırasıyla P ve Q’da kessin. AC’nin orta noktası D ve DH  PQ ise HP = HQ olduğunu gösteriniz.
12
Alıştırma. ABC dik üçgeninde m(B) = 900 ve m(C) =
150’dir. AC kenarı üzerinde bir D noktası verilsin. D’den
BC’ye inilen dikme ayağı E olsun. AB = AD ise A(ABC) =
2.BE2 olduğunu gösteriniz.
13