Ural Federe Bölgesi Öğretmen Evi X. Uluslararası Bilim Temelleri

Ural Federe Bölgesi Öğretmen Evi
X. Uluslararası Bilim Temelleri Bilgi Yarışması
2013-2014 öğretim yılı
1.etap
Matematik
10.sınıf
Andrew John Wiles‘e ithafen
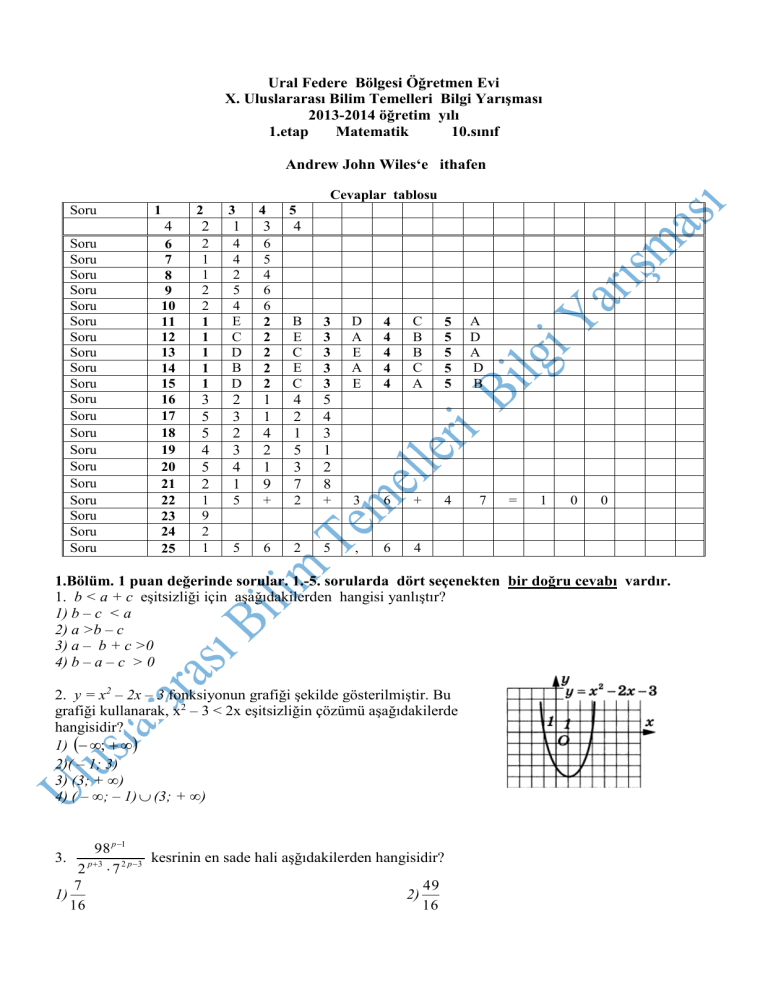
Cevaplar tablosu
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
1
2
3
4
5
4
2
1
3
4
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
2
1
1
2
2
1
1
1
1
1
4
4
2
5
4
E
C
D
В
D
6
5
4
6
6
2
2
2
2
2
B
E
C
E
C
3
3
3
3
3
3
5
5
4
5
2
2
3
2
3
4
1
1
1
4
2
1
9
4
2
1
5
3
7
5
4
3
1
2
8
1
9
2
1
5
+
2
5
6
2
D
A
E
A
E
4
4
4
4
4
C
B
B
С
A
5
5
5
5
5
A
D
A
D
B
+
3
6
+
4
7
5
,
6
4
=
1
0
0
1.Bölüm. 1 puan değerinde sorular. 1.-5. sorularda dört seçenekten bir doğru cevabı vardır.
1. b < a + c eşitsizliği için aşağıdakilerden hangisi yanlıştır?
1) b – с < a
2) a >b – с
3) a – b + c >0
4) b – а – с > 0
2. у = х2 – 2х – 3 fonksiyonun grafiği şekilde gösterilmiştir. Bu
grafiği kullanarak, х2 – 3 < 2x eşitsizliğin çözümü aşağıdakilerde
hangisidir?
1)  ;  
2)( – 1; 3)
3) (3; + ∞)
4) ( – ∞; – 1)  (3; + ∞)
98 р 1
kesrinin en sade hali aşğıdakilerden hangisidir?
2 р  3  7 2 р 3
7
49
1)
2)
16
16
3.
3)
4
16807
4)
142 р  2
7 2 р 7
4. Koordinat doğrusunda şekilde verilen b sayısı için ağıdakilerden hangisi doğrudur?
1) – b – 1 < 0
2) b + 3 < 0
3) – 2 – b > 0
4) – 4 – b >0
5. 4 pozitif, 7 negatif sayı arasından rasgele 3 farklı sayı alınıyor? Seçilen sayıların çarpımının negatif
olma olasılığı kaçtır?
1) 10/7
2) 9/15
3) 8/15
4) 7/15
2.Bölüm. 3 puan değerinde sorular. 6.-10. sorularda altı seçenekten üç doğru cevabı vardır.
6. Şekilde Rostov şehrin, 17 Kasım – 5 Aralık arasında ortalama hava sıcaklığını göstermektedir. Buna
göre doğru ifadeleri seçiniz:
1) 17 Kasım - 5 Aralık arasında en yüksek hava sıcaklığı 30С’dir.
2) 1 - 5 Aralık arasında en yüksek hava sıcaklığı 40С’dir.
3) 17 - 30 Kasım arasında en yüksek hava sıcaklığı
20С’dir.
4)17 Kasım- 5 Aralık arasında en yüksek sıcaklık 1
Aralık’ta oldu.
5) Kasım ayında en düşük sıcaklık 10С’dir.
6) Kasımın son haftasında ortalama en düşük sıcaklık 1
0
С’dir.
7. Doğru ifadeleri seçiniz:
1. İç açılarının ölçüleri toplamı 1620° olan bir çokgenin, bir köşesinden 8 köşegen çizilir.
2. Köşegen sayısı kenar sayısının iki katından üç eksik olan çokgen dörtgendir.
3.f(x) = x2 + 5x + 7 parabolünün y eksenini kestiği nokta A(a, b) olduğuna göre, a + b toplamı
5’tir.
4. Bütün köşegen uzunlukları eşit olan konveks düzgün çokgen 5 kenarlı olabilir.
5. Bir köşesinden çizilen köşegen sayısı 9 olan çokgenin kenar sayısı 12’dir.
6. Köşegen sayısı kenar sayısının 3 katına eşit olan düzgün çokgenin bir iç açısının ölçüsü 1100’dur.
8. Doğru ifadeleri seçiniz:
1. x(x-y) + y(x-y)= (x-y)(x+y)
2. 25x2-4 =( 5x + 2 )(5x – 2)
3. a2- a -1 = 0 ise a7 = 8a + 13
4. x2-(x-1)2 = 2x – 1
5. x2 - x + 1 = 0 ise x100 + x101 = 2
6. a2 -x2 -2(a-x) = ( a + 1 )(x - 1)
9. Tüm yüzleri eşkenar üçgenleri olan АВСD piramidin, O noktası AC kenarın orta noktasıdır. Buna
göre doğru ifadeleri seçiniz:
1) sin  OCD  
1
2
2) tan( ACD)  3
3) cos( ABO) 
1
2
4) tg (ODC )  1
5) sin( BOC )  1
6) cos( ABC ) 
1
2
10. Doğru ifadeleri seçiniz:
2a1  d (n  1)
aritmetik dizisinin ilk n terimlerin toplamıdır.
2
a  an1
2) Bir aritmetik dizide : an  n1
dir.
2
b (q n  1)
, q  0 aritmetik dizisinin ilk n terimlerin toplamı - Sn.
3) S n  1
q
1) S n 
 a1  an 
  n aritmetik dizisinin ilk n terimlerin toplamı - Sn.
 2 
4) Sn  
5) aritmetik dizisilerde : bn  bn 1  bn 1 dir.
6) Bir aritmetik dizide a1 ilk terim ve d ortak fark olmak üzere an  a1  (n  1).d dir.
3.Bölüm. 5 puan değerinde sorular. 11.-15.sorularda eşleştirme, 16.-20.sorularda sıralama yapılacaktır.
Cevap,her kare içine bir harf veya rakam olarak yazılacaktır ( Örnek 1A2B3C4D5E, ABCED, 12435 ).
Büyük harf ve kitap harfi (el yazısı değil ) kullanınız. Nokta, virgül ve diğer işaretleri kullanmayınız.
11. Uygun eşleştirmeleri yapınız:
Formülleri
Fonksiyon grafikleri
1)
А) y = х – 4х
2
2)
В) y = – х2+2
3)
С) y = (х+1)2
4)
D) y = – (х+2)2 + 1
5)
E) y = – х2 +4х
12. Uygun eşleştirmeleri yapınız:
Eşitsizlik sistemleri
5 х  20  0,
1) 
2 x  14  0;
Çözümleri
А) ( – 1,5;5]
 x  4,
2) 
 x  6;
 x 2  25,
3) 
2 x  3  0;
В) [7; +∞)
 4 x  16,

4)  x
 3,5;

2
6 x  24  0,
5) 
2 x  1  3.
13. Eşit ifadeleri eşleştiriniz:
D) (2; 4)
С) (4;7)
Е) ( – ∞; 4]
İfade 1
İfade 2
1) соs   sin 
А) sin 
2) 4 sin  cos  cos2
3) sin 2  sin  cos 2
В) 1
С) sin 4
4) соs 2  2 sin 2 
D) сos2
4
4
2
5) 1 
sin 2  cos
2 sin 
Е) – 1
14. Bu bilgi yarışması; İngiliz ve Amerikan matematikçi Andrew John Wiles’e ithaf edilmiştir. Andrew John Wiles
ile ilgili verilen ifadeleri tamamlayınız:
Açıklamalar
1) Andrew John Wiles, ….. yılında Cole Ödülü almıştır.
2) Andrew John Wiles, ….. yılında Wolfskehl Ödülü almıştır.
3) Andrew John Wiles,…. yılında Fermat'ın Son Teoremi profesyonel
çalışması başlamıştır.
4) Andrew John Wiles, ….. yılında Kral Faysal Ödülü almıştır.
5) Andrew John Wiles, ….. yılında Britanya İmparatorluğu Şövalyesi
olmuştur.
Tarih
A)1986
B) 1996
C) 1998
D) 2000
E) 1997
15. Aşağıdaki fonksiyonları ile en geniş tanım kümelerini eşleştiriniz:
Fonksiyon
Tanım kümesi
х 1
A) ( – ; 0)(1; + )
1) у  2
х  16
х2 1
х 2  10х
х
3) у 
х  х  5  6
B) ( – ; – 2)( – 2; 12)( 12; + )
х
х 1
х2 1
5) у 
х  10х  24
D) ( – ; – 4)( – 4; 4)(4; + )
2) у 
4) у 
C) ( – ; 0)( 0; 10)(10; + )
E ) ( – ; – 3)( – 3; – 2)( – 2; + )
16. Sayılarda * yerine cümleye uygun olarak en küçük rakamı bulup küçükten büyüğe doğru sıralayınız:
1) 3’e bölünecek şeklinde 23*47 sayısında *yerine uygun rakamı bulunuz.
2) 9’a bölünecek şeklinde 235*7 sayısında *yerine uygun rakamı bulunuz.
3) 4’e bölünecek şeklinde 233*4 sayısında *yerine uygun rakamı bulunuz.
4) 6’ya bölünecek şeklinde 265*2 sayısında * yerine 0 olmayan uygun rakamı bulunuz.
5) 11’e bölünecek şeklinde 238*56 sayısında *yerine uygun rakamı bulunuz.
17. Aşağıdaki sayıları büyükten küçüğe doğru sıralayınız:
1) sin 400
2) cos 1200
3) sin 800
4) cos 1500
5) sin 900
18. İşlemlerin sonuçları küçükten büyüğe doğru sıralayınız:
1) 12 2  3 8
2)
4 6
4 6

4 6
4 6
3) 18 3  3 12
4)
3 5
3 5

3 5
3 5
1
1
5) 3 2  84  2 5
3
4
19. İşlemleri yapıp sonuçları büyükten küçüğe doğru sıralayınız:
1) а  (7,3) ve b  (1, 5) vektörlerin skaler çarpımı kaçtır?
2) а  (8, 12) ve b  (2, 4) olduğuna göre a  b vektörün uzunluğu kaçtır?
3) а  (3, x) ve b  (7, 2) vektörleri birbirine dik vektörler olduğuna göre x kaçtır?
4) üçgenin iki kenarı 15 ve 8, aralarındaki açı 600olduğuna göre üçüncü kenarın uzunluğu kaçtır?
5) а  (2,3) ve b  (1,0) vektörlerine dik olan с vektörün koordinat toplamı kaçtır?
20. İşlemleri yapıp sonuçları küçükten büyüğe doğru sıralayınız:
1) 3  2 2  4 17  12 2 = ?
2) 74 öğrenciden 35’i dört ve beş notları aldığına göre tamsayı olarak yaklaşık yüzde kaçtır?
3) (аn) aritmetik dizisinde, а4 = – 3; d = 5; an= 47 olduğuna göre n kaçtır?
4) bir zar atıldığında üst yüzüne çift sayı gelme olasılığı kaçtır?
5) 2(х – 2) – 3х < 3 eşitsizliğini sağlayan en büyük negatif tam sayı kaçtır?
4.Bölüm. 6 puan değerinde sorular. 21.-25. sorular. Cevap, ilk kareden başlayarak rakam veya
kelime (tekil ve yalın durumda !)her kare içine bir rakam veya bir harf olarak yazılacaktır. Büyük harf ve
kitap harfi (el yazısı değil ) kullanınız. Cevap, iki veya fazla kelimeden( rakamdan ) ise virgül kullanınız.
Ondalık kesri yazabilmek için virgül işareti kullanınız.
21. A, B, C, D ve E birbirlerinden ve sıfırdan farklı tamsayılardır.
ABCDE x 4 = EDCBA ise A=? B=? C=? D=? E=?
22. 1,2,3,4,5,6,7,8, ve 9 rakamlarını birer kez kullanarak aralarına sadece + işareti koyarak 100 sayısını
elde ediniz. Cevap tablosuna işlem yazınız.
23. Ahmet ve Suat, oto yedek parça fabrikasında çalışmaktadır. Ahmet, Suat’tan bir saatte 4 fazla parça
hazırlıyor ve tüm siparişi 5 saatte tamamlıyor. Suat aynı siparişi 9 saatte hazırlayabiliyor. Buna göre
Ahmet bir saatte kaç parça hazırlayabilir?
24. 12 kibritten 5 tane kare elde edilmiştir. Büyüklükleri farklı ve sadece iki kare kalacak şeklinde kaç
kibrit alınmalıdır?
25. Hiç bir rakamı sıfır olmayan öyle iki sayı bulun ki, çarpımları bir milyon olsun. Cevap, iki sayı virgül
kullanarak yazınız.
Ural Federe Bölgesi Öğretmen Evi
XI. Uluslararası Bilim Temelleri Bilgi Yarışması
2014-2015 eğitim-öğretim yılı
1.etap Matematik
10.sınıf
Cevap Anahtarları
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
1
2
3
4
5
2
3
1
3
1
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
2
3
1
1
1
1
1
1
1
1
3
5
4
3
4
С
D
B
В
E
4
6
5
5
5
2
2
2
2
2
Е
C
A
D
C
3
3
3
3
3
2
2
1
5
3
9
4
4
5
3
4
3
5
3
2
5
1
3
2
4
1
5
1
4
1
2
E
9
6
20
V
0
0
E
,
T
1
3
А
B
E
A
B
4
4
4
4
4
В
E
C
E
A
5
5
5
5
5
D
A
D
C
D
5
1.Bölüm. 1 puan değerinde sorular. 1.-5. sorularda dört seçenekten bir doğru cevabı vardır.
1. a < 2b olduğuna göre aşağıdaki eşitsizliklerden hangisi yanlıştır?
1) 2,5a < 5b
а
b
2) >
3
6
а
>2–b
2
4) –1,3а > –2,6b
3) 2 –
2. Şekilde gösterilen grafik, ikinci dereceden fonksiyonlardan hangisine aittir?
1) у = х2 + 6х – 7
2) у = –х2 – 6х + 7
3) у = х2 – 6х + 7
4) у = –х2 + 6х – 7
37
3.

n
 122
kesrinin en sade hali aşağıdaki hangisidir?
52 n 1  7 2 n 1
7
1)
3)
5
5
2)
4)
7
2
1
35
25
49
4. Verilen eşitliklerden , ikisinin birden aynı anda doğru olmayan olan hangisidir?
2
2
, cos  
1) sin   
6
6
2) sin 
2
2
, cos  
6
6
3) sin 
2
3
, cos  
6
6
4) sin  
1
3
, cos  
2
2
5. А(–3; 6) ve В(1; 2) noktaların koordinatları verilmiştir. Buna göre AB doğru parçasının orta noktasının
koordinatları hangisidir?
1) (–1; 4)
2) (–1; 3)
3) (–2; 4)
4) (–2; 8)
2.Bölüm. 3 puan değerinde sorular. 6.-10. sorularda altı seçenekten üç doğru cevabı vardır.
6. Şekilde , otoyolda iki otobüsün ( A ve B ) hareketleri gösterilmiştir. Buna göre doğru ifadeleri seçiniz:
1) B otobüsü, A otobüsünden daha az yol
yapmıştır.
2) B otobüs yolda bir mola almıştır.
3) Hareket ettikten ilk 30 dakika sonra
otobüsler arasında mesafe 5 km olur.
4) İlk 10 dakikada A otobüsün hızı saatte
60 km.dir
5) A otobüs 5 dakikalık mola yapmıştır.
6) B otobüs yolda iki mola yapmıştır.
7. Aşağıdaki ifadelerden doğru olanları seçiniz:
1) Her hangi bir üçgende tabana ait yükseklik kenarortayla eşittir.
2) İkizkenar üçgenin taban açısı dar ise o halde bu dar açılı üçgendir.
sin 
3) Dik açılı üçgende,
, α açısının tanjantıdır.
cos 
4) Üçgenin dış açıları her zaman geniş açıdır.
5) Dik açılı üçgende, hipotenüse ait kenarortay, hipotenüsün yarısına eşittir.
6) Eşkenar dörtgenin köşegenleri dik olarak kesişirler.
8. Doğru ifadeleri seçiniz:
1) Bir torbada 14 kırmızı, 9 sarı ve 7 yeşil top vardır. Torbadan rastgele bir top çekilirse, seçilen topun
sarı olma olasılığı 0,3’tür.
2) 4 ve 23 sayıları arasında 3’e bölünebilen doğal sayı seçme olasılığı 0,4’tür.
3) Telefon üzerinde 10 tane rakamlı tuş ( 0-9 arası ) vardır. Bu rakamlı tuşlardan herhangi birine rastgele
basıldığında, rakamın 5’ten büyük ve çift sayı olma olasılığı 0,3’tür.
4) Fabrikada yapılan kahve makinelerinden 1000 tanesinden 7’si bozuk çıkmaktadır. Rastgele seçilen
kahve makinesinin bozuk olmama olasılığı 0.993’tür.
5) Bir madeni para 3 kere masanın üzerine atılıyor. 2 kez tura gelme olasılığı 0,375’tir.
6) 2 zar aynı anda masanın üzerine atılıyor. Üste gelen yüzdeki sayıların toplam 4 olma olasılığı 0,25’tir.
9. Doğru ifadeleri seçiniz:
4
3
1) sin t  , 900  t  1800 olduğuna göre cos t  
5
5
6 0
4
2) sin t  , 0  t  900 olduğuna göre cos t  
5
10
7
24
, 0 0  t  900 olduğuna göre sin t 
3) соst 
25
25
5 0
, 0  t  900 olduğna göre ctgt  2 ,4
12
4
3
5) tgt  , 0 0  t  900 olduğna göre ctgt 
3
4
8
15 0
6) сtgt 
, 0  t  900 olduğna göre tgt 
15
17
4) tgt 
10. Doğru ifadeleri seçiniz:
1) Bir АВСD paralelkenarında, AD vektörü ile CB vektörleri aynı doğrultulu vektörlerdir.
     
2) a  b  c  a  b  c eşitliğine üçgen eşitsizliği kuralı denir.
3) Hacim vektörel büyüklüktür.
4) Bir çemberin yarıçapı 2 cm artılırsa, çevresi 4π cm artar.
5) Eşkenar dörtgenin simetri merkezi vardır..
6) D(–3; 4) noktası 3. Bölgede (üçüncü çeyrekte) bulunmaktadır.




3.Bölüm. 5 puandeğerindesorular. 11.,12.,13.,14.,15. ve18.sorularda eşleştirme, 16.,17.19. ve
20.sorularda sıralama yapılacaktır. Cevabı,her kare içine bir harf veya rakam olacak şekilde
yazınız. ( Örnek 1A2B3C4D5E, ABCED, 12435 ). Büyük harf ve kitap harfi (el yazısı değil )
kullanınız. Nokta, virgül ve diğer işaretleri kullanmayınız.
11. Fonksiyon grafiklerini, denklemleriyle eşleştiriniz:
Fonksiyon grafikleri
1)
Formül
1
А) у 
х1
2)
В) у   х
3)
С) у  х  2
4)
D) у 
5).
E) у  x 2  4 x  5
1
1
х
12. Eşitsizliklere uygun çözüm kümelerini bulunuz:
Eşitsizlik
1) ( 3  10 )( 2 х  7 )  0
3
2)
0
2х  1
2х  1
0
3)
х2
4
0
4)
3х  7
5) ( x 2  4 )( х  3 )  0
Çözüm
А) ( 2; 2 )  ( 3;   )
В) ( 0 ,5; 2 )
С) ( 0 ,5;   )
D) ( 3 ,5;   )
1
Е) ( ; 2 )
3
13. Eşit ifadeleri eşleştiriniz:
İfade 1
İfade 2
1) tg    cos   sin 
А) cos2α
2) 1  2sin   cos   tg
В) 0



3) sin 2   cos 2  sin 2  
С) 2
2
2

сos
4) (sin 
)  2 sin 
D) 2cosα
tg
1
5)
 sin  cos(  ) 
Е) sin2α
tg
14. Uygun eşleştirmeleri yapınız:
Açıklama
Matematik terim
1) Çember çevresinin uzunluğunun, çapının uzunluğuna bölünmesi ile A) Rasyonel sayıdır
elde edilen sabit sayı ………….
2) 1 ve kendisinden başka hiçbir sayma sayısı ile bölünemeyen 1’den
B) Pi sayısıdır
büyük tam sayı …………
3) a ve b tam sayı ve sıfır olmamak üzere a/b şeklindeki sayı ……..
C) Cebirsel sayıdır
4) İki tam sayının birbirine bölümü şeklinde yazılmayan sayı ………
D) Asal sayıdır
5) Katsayıları tam sayılar olan bir polinomun kökü olarak ifade edilebilen E) İrrasyonel sayıdır
sayı ……………..
15. Aşağıda verilen dizi sorularını doğru cevaplarıyla eşleştiriniz.
Dizi
Dizinin ilk n
terim toplamı
1) (bn) geometrik dizisinde ilk terim b1 = 3 ve ortak çarpanı q = 2 verilmiştir.Buna A) –100
göre bu dizinin ilk beş terim toplamını bulunuz.
2) ilk terimi 4, ortak farkı 3 olan bir aritmetik dizisinin ilk 15 terim toplamını B) 54
bulunuz.
3) Aritmetik dizinin oluşturan –10; –6; –2; 2;… dizisinin ilk 9 teriminin toplamını C) 375
bulunuz.
4) 5, -15, ... geometrik dizisi verilmiştir. Bu dizinin ilk 4 terim toplamı bulunuz.
D) 115
5) а5 = 10, а10 = 25 olduğuna göre (аn) aritmetik dizisinin ilk 10 terim toplamı E ) 93
bulunuz.
16. Aşağıdaki ifadeleri değerlerine göre küçükten büyüğe doğru sıralayınız:
18
1)  4 3  27 2 


3
2) 5  2 7  ( 5  2 7 )  15 7
0 ,08  320
5
16   7
3
4
4)   2 ,8      0 ,018  
5  3
8
7
3)
5)
3 ,6  106
4  10 4
17. Aşağıdaki problemleri çözünüz ve bulunan değerlerini büyükten küçüğe doğru sıralayınız:
 
 
11
2) Bir ABC dik üçgeninde m  ACB   90 , sin  CAB  =
, ǀАСǀ = 10 3 olduğuna göre ǀАВǀ bulunuz.
14
3) Bir ABC dik üçgeninde m  ACB   90 , ǀАВǀ = 30, ǀАСǀ = 24 olduğuna göre tan  CAB  yi bulunuz.
20
4) Bir ABC dik üçgeninde m  ACB   90 , cos  CBA  =
, ǀАВǀ = 29 olduğuna göre ǀАСǀ bulunuz.
29
5) Bir ABC dik üçgeninde m  ACB   90 , АС = 15, sin  CAB  = 0,6 olduğuna göre ǀBCǀ bulunuz.
1) Bir ABC dik üçgeninde m ACB  900 , ǀАВǀ = 20, ǀАСǀ = 16 olduğuna göre sin CAB yi bulunuz.
0
0
0
0
18. İfadeleri, değerlerine göre küçükten büyüğe doğru sıralayınız:
1


2
51  7  2 




1)
2
1
44
4)
2
2)
13 1126  5 2 15
21  8 5  21  8 5
 112
1

2  52   9




3)
1
25 4
5)
3
32 : 3 4  121
19. Aşağıdaki problemleri çözünüz ve bulmuş olduğunuz değerleri büyükten küçüğe doğru sıralayınız:
1)  ВАС = 1200,  АВС = 300, ǀАВ = 5 olduğuna göre ABC üçgenin ǀACǀ kenar uzunluğu kaçtır?
2) Bir ABCD dörtgeninde ǀАВǀ = 10, ǀСDǀ = 8, ǀВСǀ = 5 ve dörtgenin içinde kenarlara teğet olacak şekilde
bir çember çizilebildiğine göre dörtgenin ǀADǀ kenar uzunluğu kaçtır?
3) АВ  (3,8) ve MN  (2,3) vektörlerinin skaler çarpımı bulunuz.
4) Bir dışbükey çokgenin iç açıların toplamı 7200 olduğuna göre çokgenin kaç kenarı vardır?
5) Bir yamuğun alt ve üst tabanların oranı 1/11 ve orta tabanı 48 olduğuna göre büyük taban uzunluğu
kaçtır?
20. Denklemleri kök değerlerine göre küçükten büyüğe doğru sıralayınız:
56  2 х  6
4
1
2) х  23
5
5
х  43
3
3)
х5
4) х2 + 12х + 32 = 0 ( denklemin birden fazla kökü varsa büyük kökü dikkate alınız)
5) 2х2 – 13х + 11 = 0 ( denklemin birden fazla kökü varsa küçük kökü dikkate alınız)
1)
4.Bölüm. 6 puandeğerindesorular. 21.-25. sorular. Cevap olacak rakam veya kelime ilk kareden
başlayarak (tekil ve yalın durumda!)her kare içine bir rakam veya bir harf gelecek şekilde
yazılacaktır. Büyük harf ve kitap harfi (el yazısı değil ) kullanınız. Cevap, iki veya daha fazla
kelimeden oluşuyor ise virgül kullanınız. Ondalık kesri yazabilmek için virgül işareti kullanınız.
21. Bir usta 60 parçayı kalfasından 3 saat daha kısa bir sürede onarabilmektedir. İkisi birlikte
çalıştıklarında bir saatte 30 parçayı onarabildiğine göre, kalfa tek başına 90 parçayı kaç saatte onarabilir?
22. –13,5 ve –3,7 sayıları arasına 7 tane sayı koyularak bir aritmetik dizi oluşturulmuştur.. Bu dizinin
ortak farkı, у = 1 + х – х2 fonksiyonun değerler kümesine ait mi? Cevap tablosuna evet veya hayır
yazınız.
23. Bir antikacı 225 ruble ile iki antika parça satın alıp bu parçalardan %40 kar elde etmiştir. Birinci
parçadan % 25, ikinci parçadan ise % 50 kar elde ettiğine göre , her parçanın kaç rubleye alındığını
bulunuz. Cevap tablosuna sadece değerleri araya virgül koyarak yazınız.
24. Bir araç, ilk üç saat 50 km/s, sonraki yarım saat 60 km/s ve daha sonraki iki saat ise 75 km /s hızla
hareket ettiğine göre, aracın tüm yol boyunca ortalama hızı kaç km/ s olur ? Cevap tablosuna sadece
değeri (birimsiz) yazınız.
25. 200 metrelik bir koşuda birinci gelen atlet, koşuyu ikinciden 10 metre, üçünden de 29 metre önde
bitirmiştir. Buna göre, ikinci gelen atlet, koşuyu üçüncüden kaç metre önde bitirmiştir?
( Atletlerin sabit hızla koştukları varsayılacaktır ).
Final
Ural Federe Bölgesi Öğretmen Evi
X. Bilim Temelleri Bilgi Yarışması
PREMİER LİG 2013-2014 öğretim yılı
Matematik
İngiliz matematikçi Andrew John Wiles ‘e ithafen
10.sınıf
Cevap anahtarları
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15.1
15.2
15.3
15.4
16.1
16.2
16.3
16.4
1
4
2
2
2
1
1
1
5
5
1
1
B
2
2
1
3
1
0
0
2
2
5
4
3
3
B
D
E
3
3
C
C
C
5
4
6
5
5
4
2
2
2
2
1
2
2
D
4
E
C
C
4
4
F
D
A
3
3
3
3
1
2
3
3
F
A
A
4
4
4
C
E
B
5
5
5
A
B
D
E
A
4
4
D
E
5
5
A
B
1
6
7
8
B
F
6
6
7
7
C
H
8
8
D
G
5
1.Bölüm. 3 puan değerinde sorular. 1.-5. sorularda altı seçenekten üç doğru cevabı vardır.
Doğru yanıtların numaralarını cevap tablosuna yazınız.
1. Aşağıdaki ifadelerden hangileri diğerlerinden büyüktür?
3) 2 cos  1
4) 2  5 cos
1) sin  1
2) 1 cos
5)   2  2
6) 2  2
2. Şekile göre f(x) > g(x) eşitsizliğini sağlayan tam sayılar aşağıdakilerden hangileridir?
1) 1
2) 2
3) 3
4) ‒1
5) ‒2
6) ‒3
3. Sinema gişesinde sırada Namık, Ahmet, Bora, Volkan, Gökay ve Deniz vardır. Ahmet, Bora’dan önce
ama Deniz’den sonradır. Volkan ile Deniz sırada yan yan değiller, Gökay ise Deniz, Ahmet ve Volkan ile
yanında değildir. Namık en son bileti alır. Buna göre sıradaki ilk üç arkadaş hangileridir?
1) Namık
2) Ahmet
3) Gökay
4. Aşağıdaki şekillerden eşit alanlı olanları bulunuz.
4) Volkan
5) Deniz
6) Bora
1)
2)
3)
4)
5)
6)
 x 2  2 x  15
5. y 
fonksiyonun çözüm kümesine uygun (x,y) ikilileri aşağıdakilerden hangileridir?
x5
3
15
1) (2, 3)
2) (1,1)
5) (‒7,1)
6) (4, 2)
3) (0,
)
)
4) ( 1,
5
2
2.Bölüm. 5 puan değerinde sorular. 6.-8.sorularda uygun eşleştirme, 9.-10.sorularda uygun
sıralama yapılacaktır.
Cevap,her kare içine bir harf veya rakam olarak yazılacaktır ( Örnek 6.8.sorularda -1A2B3C4D5E, 9.-10.sorularda- 13425 ). Büyük harf ve kitap harfi (el yazısı değil )
kullanınız. Nokta, virgül ve diğer işaretleri kullanmayınız.
6. Uygun eşleştirmeleri yapınız:
Dizi
Genel terim
1) 2, 4, 8, 16, 32, …
A) yn   1  3 n
2) ‒1, 2, ‒3, 4, ‒5, 6, …
B) y n  2 n
3)
1
1
1
1
,
,
,
,…
2  5 4  7 6  9 8  11
n
C) yn  3 2 
n
1
2n(3n  2)
4) ‒6, 12, ‒24, 48, …
D) yn 
5) ‒3, 9, ‒27, 81, …
E) yn   1  n
n
F) y n 
1
2n(2n  3)
7. Fonksiyon ile tanım kümesini eşleştiriniz:
1) y  ( 2  х)5
A) (;2]
2) y  ( 8  2 х)
B) (;2)  (2;2)  (2;)
3) y  4  2 х
1
4) y 
9  3х
5х
5) y  2
х 4
C) (;4)  (4; )
-6
D) (;)
E) (;3)
8. Trigonometrik fonksiyonlar ile periyotlarını eşleştiriniz:
х
3
2) y  sin 4 x
4
3
1) y  cos
A)
3) y  cos1,5 х
B) 

C)
2
D) 3
4) y  sin x
5) y  sin
2
x
3
E) 6
F) 4
9. f(2) ‒ f(1) değerlerin azalmasına göre fonksiyonları sıralayınız:
3x  x 2
x 1
5 x 2 (1  x)
2) f ( x) 
2 x  3x 2
3) f ( x)  4 x 2  8 x  9
1) f ( x) 
4x  x 2
x
5) f ( x)  3x( x 2  5)
4) f ( x) 
10. Aritmetik dizileri, terimler arasındaki farka göre büyükten küçüğe sıralayınız.
1) 6, 8, 10, …
2) 25, 21, 17, …
3) 7, 10, 13, …
4) 12, 9, 6, …
5) 16, 21, 26, …
3.Bölüm. 8 puan değerinde sorular.
11.-12. uygun eşleştirme, 13.-14.sorularda uygun sıralama yapılacaktır. Cevap, her kare içine bir
harf veya rakam olarak yazılacaktır ( Örnek 11.-12.sorularda -1A2B3C4D5E, 13.-14.sorularda13425 ).
11. Aşağıdaki ifadeleri eşleştiriniz.( Harfler tekrarlanabilir).


1) sin x   
2

2) cos(  x) 
3) sin(  x) 
 3

4) cos
 x 
 2

 3

5) tg 
 x 
 2

6) tg (  x) 


7) sin  x  
2



8) cos  x  
2

A)  ctgx
B)  tgx
C) cos x
D) sin x
E)  sin x
F)  cos x
12. Aşağıdaki problemlerin cevaplarını bulunuz:
1) % 8 zam yapıldığından sonra televizyon fiyatı 10800 TL olduğuna göre zamdan önce
televizyonun fiyatı kaç liraydı?
2) Eylül ayında üzümün 1 kg fiyatı 60 ruble, ekim ayında % 30, kasım ayında ise % 20 daha
zam oldu. Kasım ayındaki zamdan sonra üzümün kilosu kaç ruble oldu?
3) Defterin fiyatı 10 lira. 30 adetten fazla defter aldığında % 15 indirim uyguladığına göre
900 liraya en fazla kaç defter alınır?
4) Gelir vergisi % 13’tür. Ahmet beyin net maaşı 21750 ruble olduğuna göre vergi
kesilmemiş haliyle kaç rubledir?
5) Sezen’in oturduğu ev 16 katlı ve her katta 8 daire vardır. Daire numarası 109 olduğuna göre
Sezen kaçıncı katta oturmaktadır?
6) Bir kesrin payı % 20 artırılmıştır. Kesrin değerinini iki katına çıkartmak için paydasının
% kaç küçültmesini gerekicektir?
7) Elma kuruturken kendi ağırlığının% 85 kaybeder. 500 kg taze elmadan kaç kg kuru elma
elde edilir?
8) C vitamini günlük alım miktarı 60 mg'dır. Bir mandalina ortalama 35 mg C vitamini içerir.
Üç mandalina yiyen bir çocuk,haftalık C vitamini ihtiyacının yaklaşık yüzde kaçını alır?
A) 103
B) 14
C) 10000
D) 93,6
E) 25000
F) 40
G) 25
H) 75
13. Bu bilgi yarışması; İngiliz ve Amerikan matematikçi Andrew John Wiles’e ithaf edilmiştir.
İngiliz ve Amerikan matematikçi, Oxford Üniversitesi'nde Royal Society araştırma profesöru, Clay
Matematik Enstitüsü Bilim Kurulun üyesidir. 1974 yılında tamamladığı Cambridge Üniversitesi'
nin Merton Kolejindeki lisans eğitimi bitirdi. Andrew Wiles’in kariyerinin en önemlisi Fermat'ın Son
Teoremi kanıtı oldu. Tabloda Andrew Wiles’in Amerika’ya taşındığı yılı yazılmıştır. Aşağıdaki işlemleri
yapıp her rakama eşit olan sonucun harfı yazınız.
1
9
8
2
А)
 3 2  9   1 
 2
1
C)
 11  :  11 
2 5
1
3 3
1
1
  9
 11 
B)
 12  :  12 
4 8
17 2
2
1
   1
 12 
D)
1
2
1 1 1
        40
5 5  7
14. Polinomların ile (х ‒ 2) bölüm kalanları bulunuz ve kalanların artışına göre polinomları sıralayınız:
1) 8х2 ‒ 12х ‒ 3
2) х5 ‒ 2х4 ‒ 8х2 + 16х ‒ 3
3) 3х3 ‒ 5х2 ‒ 2х + 4
4) х3 ‒ 2х2 + 3х ‒ 4
5) х4 ‒ 2х3 ‒ 8х + 16
6) 3х2 ‒ 5х + 4
7) х3 ‒ 2х2 + 4х ‒ 1
8) 4х4 ‒ 6х3 ‒ 4х2 + 8
15. 15.1–15.4 alt sorularda verilmiş seçeneklerden bir doğru vardır. Cevap numaraları cevaplar
tablosuna yazınız. Büyük harf ve kitap harfi (el yazısı değil ) kullanınız. Nokta, virgül ve diğer
işaretleri kullanmayınız.
15.1. х 2  6 х  5  а denklemin kökü yoksa a kaç olmalıdır?
1) а > 0
2) a < 0
3) a > 4
4) 0 < a < 4
15.2. х 2  6 х  5  а denklemin iki farklı kök var ise a kaç olmalıdır?
1) а = 0, а > 4
2) а < 4
3) а = 0
4) а > 6
15.3. . х 2  6 х  5  а denklemin üç farklı kök var ise a kaç olmalıdır?
1) 0 ≤ а ≤ 4
2) 0 < a < 4
3) a = 4
4) a < 0
15.4. . х 2  6 х  5  а denklemin dört farklı kök var ise a kaç olmalıdır?
1) 0 < a < 4
2) a = 0, a = 4
3) a ≥ 0
4) a > 5
4.Bölüm. 16.soru 20 puan değerindedir. 16.soruda 4 alt soru vardır ve her alt soru 5 puan
değerindedir. Cevap her kare içine bir harf olarak boşluk bırakmadan yazınız. Virgül ve diğer
işaretleri kullanmayınız. Büyük harf ve kitap harfi (el yazısı değil ) kullanınız.
16.1. ( х 2  16) х 2  4 х  5  0 denklemin en küçük kökü bulunuz ve cevap tablosuna yazınız.
16.2. ( х 2  16) х 2  4 х  5  0 denklemin köklerinin toplamı bulunuz ve cevap tablosuna yazınız.
16.3. ( х 2  16) х 2  4 х  5  0 denklemin köklerinin aritmetik ortalaması bulunuz ve cevap tablosuna
yazınız.
16.4. ( х 2  16) х 2  4 х  5  0 denklemin pozitif köklerinin geometrik ortalamasını bulunuz ve cevap
tablosuna yazınız.
Ural Federe Bölgesi Öğretmen Evi
IX. Bilim Temelleri Bilgi Yarışması
Final
PREMİER LİG 2012-2013 öğretim yılı
Matematik
10.sınıf
Maxim Kontsevich ‘e ithafen
Cevap anahtarları
soru
soru
soru
soru
soru
soru
soru
soru
soru
soru
soru
soru
soru
soru
soru
soru
soru
soru
soru
soru
soru
soru
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15.1
15.2
15.3
15.4
16.1
16.2
16.3
16.4
1
2
1
1
2
1
1
1
2
4
1
1
5
8
4
4
3
2
1
2
0
4
2
4
2
3
3
D
C
B
3
5
D
D
1
3
4
5
4
5
5
2
2
2
4
1
2
2
2
5
А
E
E
5
2
C
H
8
1
3
3
3
1
3
3
3
4
4
B
D
А
4
4
4
C
B
D
5
5
5
E
А
C
А
F
3
2
4
4
7
7
F
А
6
6
5
5
E
B
6
6
G
G
7
7
H
C
8
8
B
E
0
2
1.Bölüm. 3 puan değerinde sorular. 1.-5. sorularda beş seçenekten üç doğru cevabı seçiniz.
Cevaplar her rakam her kare içinde boşluk bırakmadan yazınız.
x
fonksiyon için doğru ifadeleri seçiniz:
2
1) fonksiyonun en büyük değeri 3’tür
2) fonksiyon periyodu 4 ‘e eşittir
3) x=k ( k  Z ) fonksiyonun sıfırlar
4) fonksiyon tektir.
5) [ – 2;2]aralıkta fonksiyon artandır
1. y  3 sin
2. Yanlış olan eşitlikleri seçiniz:
3
1) sin(  x)   cos x
2
2) cos(  x)   sin x

3) tg (  x)  ctgx
2
4) ctg (  x)  tgx
5) sin(2  x)   cos x
3. АВС üçgen ile ilgili yanlış ifadeleri seçiniz:
1) АВ  АС  АВ  2  АВ  АС  cos A
2) AB  sin C  AC  sin B
2
2
3) ВC  АС  АВ  2  АВ  АС  cos A
2
4) AB 
2
2
AC
sin C  sin B
BC

5)
sin B sin A
AC
4. Aşağıdaki fonksiyonlardan üstten sınırlı olan hangileridir?
1) у= – 3x2+5x-8
2) y=tg(2x)
3) y=arcsin(x)
4) y=8x2+17x-12
5) y   5x  4
5. Genel terimi y n  1  cos2

n
olan dizinin beş terim bulunmuştur. Bunlardan hangileri doğrudur:
1) y1  2
2) y 2  1
3
3) y 3 
4
2 2
4) y 4 
2

5) y 5  sin 2
5
2.Bölüm. 5 puan değerinde sorular. 6.-8. sorularda uygun eşleştirmeleri yapınız.
Cevap her kare içine bir harf olarak yazınız. Büyük harf ve kitap harfi (el yazısı değil ) kullanınız.
6. у  sin x trigonometrik fonksiyonudur. Dönüşümden sonra trigonometrik fonksiyon görünümü nasıl
olacaktır? Uygun eşleştirmeleri yapınız:
Trigonometrik fonksiyonu grafik dönüşümü
1) OY ekseni boyunca 2 katı sıkıştırma ve simetrinin apsis
eksenine göre dönüşümü.
2) ОУ ekseni boyunca 2 kat uzatılma, OX ekseni boyunca 2
katı sıkıştırma
3) ОX ekseni boyunca 2 uzatılma, OY ekseni boyunca 2 katı
sıkıştırma
4) ОУ ekseni boyunca 2 kat uzatılma, simetrinin apsis
eksenine göre dönüşümü.
5) ОX ekseni boyunca 2 kat sıkıştırma ,OY ekseni boyunca 2
katı uzatılma
Trigonometrik fonksiyonu
А) у  2 sin 2 x
B) у  0,5 sin 0,5 x
C) у  2 sin x
D) у   0,5 sin x
E) у  0,5 sin x
7. Uygun eşleştirmeleri yapınız:
Noktaların geometrik pozisyonu
Denklem veya eşitsizlik
А) x  y 2
1)
B) xy  0
2)
C) х2=у2
3)
D) 1  x 2  y 2  4
4)
E) х2+у2 – 2у+1=1
5)
8. (f) yüzey, ребер (k) kenar ve (e) tepe sayısına göre düzgün çokgen çeşitleri belirtiniz:
Çokgen özellikleri
1)f = 4, k = 6, e = 4
2) f = 8, k = 12, e = 6
3) f = 20, k = 30, e = 12
4) f = 6, k = 12, e = 8
5) f = 12, k = 30, e = 20
Çokgen
А) düzgün yirmiyüzlü
B) düzgün dörtyüzlü
C) düzgün onikiyüzlü
D) Küp
E) düzgün sekizgen
9.soruda uygun sıralamaları yapınız. Cevap her kare içinde bir rakam olarak boşluk bırakmadan
yazınız. Virgül ve diğer işaretleri kullanmayınız.
9. Bu bilgi yarışması; Fields ödülü alan rus kökenli fransız matematikçi Maxim Kontsevich’e ithaf
edilmiştir. Maxim Kontsevich ile ilgili verilen ifadelerin kronolojik sıralamasını yapınız:
1)Maxim Kontsevich Forbes derginin reytingine göre dünyaca en ünlü rus kökenli 10 bilimadam
arasında yer aldı.
2) M.Kontsevich Moskova Devlet Üniversitesi mekanik-matematik fakültesi bitirdi.
3) M.Kontsevich Bonn Üniversitesi'nde PhD derecesini aldı.
4) M.Kontsevich Poincare ödülü almıştır.
5) Witten'in hipotezsi kanıtığı için Fields ödülü aldı.
3
 
10. sin x  , x   ;   olduğuna göre ifadelerin değerlerini bulup büyükten küçüğe doğru sıralayınız:
5
2 
1) cos x
2) sin (2x)
3) ctg x
4) cos(2x)
5) tg x
3.Bölüm. 8 puan değerinde sorular.
11.-12.sorularda uygun eşleştirmeleri yapınız. Cevap her kare içinde bir harf olarak boşluk
bırakmadan yazınız. Büyük harf ve kitap harfi (el yazısı değil ) kullanınız.
11. Aritmetik veya geometrik olduğunu belirtip dizileri ile ortak fark / ortak çarpan eşleştiriniz:
Dizi
Ortak fark / payda
1) 2; 10; 50; …
А) 7
B) – 0,1
1
1 1
2)
;  ; ;...
16
8 4
3) 7’e bölünen iki basamaklı dizisi
C) – 2
4) – 50; – 35; – 20; …
D) 5
5) 2; 2 2 ; 4; 4 2 ;...
E) 2
F) 15
6) a n  3n  5 formüllü dizisi
G) 3
7) bn  2  32n formüllü dizisi
8) – 100; 10; – 1; 0,1; …
H) 9
12. İkinci sınıf tren vagonunda 54 oturma yeri ( 9 kabin: 4 ön ( 2 alt/ 2 üst) ve 2 yan ( 1 alt / 1 üst) oturma
yeri ) vardır. Çift sayılı - üst, tek sayılı – alt oturma yerleridir. Bir yolcu tren bileti alırken oturma yeri
rastgele belirtilmiştir. Buna göre doğru eşleştirmeleri yapınız.
Olay
1) alt yan oturma yeri olma
2) üst yan oturma yeri olma
3) alt oturma yeri olma
4) 1.-35. oturma yerleri satıldığında, alt oturma yeri olma
5) 3/1’i oturma yerleri satıldığında, alt oturma yeri
olma
6) 1.-32. oturma yerleri satıldığında, üst yan oturma yeri olma
7) 1.-20. oturma yerleri satıldığında, yan oturma yeri olma
8) 1.-20. alt oturma yerleri satıldığında, ön oturma yeri
olma
Olasılık
1
А)
4
2
B)
3
9
C)
17
1
D)
3
13
E)
22
1
F)
2
9
G)
22
1
H)
6
13.-14.sorularda doğru sıralamaları yapınız.Cevap her kare içinde bir harf olarak boşluk
bırakmadan yazınız. Büyük harf ve kitap harfi (el yazısı değil ) kullanınız.
13. Sayıları küçükten büyüğe doğru sıralayınız:
5
)
12
13
2) cos (
)
24
5
3) sin(
)
24
17
4) sin(
)
6
5) cos (  )
1) sin( 

)
6

6) ctg(
7) tg(
)
4
8) sin(0)
14. Metinde boş bırakılan yerleri uygun ünlü matemitikçilerin isimleri ile tamamlayınız. Cevaplar
tablosuna, metin içinde bunların sırayla gelen numaraları yazınız.
XII. yüzyılda yaşamış Hint matematikçi _____________ (1114 – 1185) «Lilavati » eserinde
kombinasyon ve permütasyon ile ilgili problemlerin araştırmalarını yapmış. Kombinatorik, genellikle
sonlu soyut nesneleri konu alan pür matematik dalı XVI.yüzyılında ortaya çıkmış. Zar oyunlarında farklı
seçenek olasılığı ile ilk araştırmaları italyan matematikçi __________________(1499-1557) başlamıştır.
Kombinatorik teoretik araştırmaları XVII. yüzyılında fransız bilimadamları Blaise Pascal (1623-1662) ve
____________(1601-1665) yapmışlardır.Bundan miza problemi önemli bir rol oynamıştır. Bu
problemi
_____________________ çözmüştür. Bu problemin çözümü « matematiksel beklenti » kavramının
tanıtılmasına yol açmıştır. Daha sonraki kombinatorik gelişiminde, İsviçreli matematikçi
________________ 1654-1705), Alman matematikçi _____________(1646-1716),
_________________(1707-1783) yer almışlardır. Ancak onların araştırmalar da farklı oyunlara( loto,
soliter oyunu, v.s.) bağlıydı.
Modern kombinatorik babası olarak, kombinatoryal olasılık analizi yapan, Macar matematikçi
____________ (1913-1996) kabul edilir.
1) Blaise Pascal
2) Gottfried Leibniz
3) Niccolo Tartaglia
4) Jakob Bernoulli
5) Pierre de Fermat
6) Pal Erdos
7) Leonard Euler
8) Bhaskara
15.1–15.4 alt sorularda verilmiş seçeneklerden bir doğru
tablosuna yazınız.
15. Problemleri çözünüz:
vardır. Cevap numarası cevaplar
15.1 Arzu, bildiği ünlü matematikçilerin isim listesi yapmış: Mileti Thales, Öklid, Newton, Lobaçevski ,
Francois Vieta. Bunlar arasında hangisi diğerlerinden en son yaşadı?
1) Mileti Thales
2) Öklid
3) Newton 4) Lobaçevski
5) Francois Vieta
15.2 Şekillerde gösterilen böyle kenarları ve açıları olan tek bir üçgen vardır. Hangisidir?
1)
2)
3)
4)
5)
15. Dip alanı 2 dm2 olan dikdörtgenler prizması biçiminde bir akvaryum 5 cm
yüksekliği kadar su ile doldurulmuş. Dip alanı 1 dm2 ve yükseklik 7 cm olan
dikdörtgenler prizması biçiminde boş kavanozu akvaryumum dibine
yerleştirilmiş.Akvaryumdaki yükselen suyun bir kısmı boş kavanoza akar.
Buna göre kavanozda su kaç cm yükseltmiştir?
1) 1 сm
2) 2 сm
3) 3 сm
4) 4 сm
5) 5 сm
15.4 Cümle tamamlayınız: n – bir prizmanın ayrıt sayısı ise ,o halde n…..
1) n – mutlaka çifttir
2) n – mutlaka 3’ bölünür
3) n – mutlaka tektir
4) n – mutlaka 10’dan büyüktür
5) n –2006 ‘ya eşit olabilir
4.Bölüm. 16.soru 20 puan değerindedir.
16.soruda 4 alt soru vardır ve her alt soru 5 puan değerindedir. Cevap her kare içine bir harf
olarak boşluk bırakmadan yazınız. Virgül ve diğer işaretleri kullanmayınız. Büyük harf ve kitap
harfi (el yazısı değil ) kullanınız. Ondalık kesir virgül ile yazınız.
16. Problemleri çözünüz:
16.1 Denklemi çözünüz: х1099  2 х1199  3х1299  ...  20х1999  21х 2009  232 .
16.2 Newton problemi: Çayırın her yerinde ot aynı şekilde büyüyor. Bu otu 70 inek 24 günde, 30 inek
ise 60 günde yerler. Buna göre 96 günde bu otu kaç inek yiyebilir? (Not: inekler eşit miktarda ot
yiyorlar).
16.3 x  R , olmak üzere , 4  x 2 
8  sin 2 x
denkleminin çözüm kümesini bulunuz.
2  x4
16.4 1 Eylül tarihinde sabah matematik öğretmeni tahtaya 6 ve 7 sayılarını yazmış. Ondan sonra nöbetçi
öğrenci her sabah yazılan sayıları silip yerine bu sayların aritmetik ve harmonik ortalaması yazacaktır. 22
Ekim Tarihinde gündüz tahtada yazılan sayıların çarpımım kaçtır?
(a ve b sayıların aritmetik ortalaması
2
ab
, harmonik ortaması ise
dir. )
1 1
2

a b
Ural Federe Bölgesi Öğretmen Evi
XI. Uluslararası Bilim Temelleri Bilgi Yarışması
2014-2015 eğitim-öğretim yılı
Final Premier lig
Matematik 10.sınıf
Cevap anahtarları
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
Soru
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15.1
4
3
1
1
3
1
1
1
1
2
1
1
2
2
4
5
5
3
2
5
B
C
B
2
,
B
C
1
3
6
6
4
3
6
2
2
2
5
6
2
2
3
4
A
E
C
4
,
A
B
4
1
3
3
3
3
5
3
3
E
D
A
4
4
4
C
B
E
5
5
5
D
A
D
,
D
D
1
4
4
3
C
A
,
1
5
,
3
0
Soru
Soru
Soru
Soru
Soru
Soru
Soru
15.2
15.3
15.4
16.1
16.2
16.3
16.4
3
1
2
4
-
1
0
5
,
5
1.Bölüm. Her soru 3 puan değerindedir. 1.-5. soruların altı seçenekten üç doğru cevabı vardır.
Doğru yanıtların numaralarını cevaplar tablosuna yazınız.
1. Aşağıdakilerden hangisi geometrik dizidir?
1
n
1) an = 2n – 1
3) an =
2) 3, 6, 9, ... , 3k, ...
4) 2, 4, 8, ... , 2n, ...
5) 3, –1,
1
1
,  , ...
9
3
6) a, 0, 0, ...
2. Kökü -4 olan denklemler aşağıdakilerden hangileridir?
1) (x + 2) 2 + (x + 6)2 = 2x2
3) x2 = –11x – 28
2) 41 + 2x = 642x
4) 9x – 2·(–5 + 7x) = –8x – 5
5)  24  10 х   х
6) 65x + 18 =1:36
3. Soçi şehrinde yapılan Kış olimpiyatlarında Kanada takımı Almanya takımından daha fazla ama Rusya
takımından daha az madalya almıştır. Almanya, Kanada takımının gerisinde kalan Norveç takımından
daha az madalya almıştır. Buna göre aşağıdakilerden hangileri doğrudur?
1) Rusya takımın Norveç takımına göre madalya sayısı daha fazladır
2) Belirtilen takımlardan Kanada takımı üçüncü olmuştur
3) Belirtilen takımlardan Almanya takımı sonuncu olmuştur
4) Norveç takımı Almanya takımının önüne geçmiştir
5) Norveç takımın Rusya takımına göre madalya sayısı daha fazladır
6) Belirtilen takımlardan Kanada takımı birinci olmuştur
4. Geometrik fraktalları seçiniz:
1) Serpinskiy halısı
2) Koch eğrisi
3) Menger süngeri
4) Newton havuzları
5) Mandelbrot kümesi
6) Julia kümesi
5. Cevabı 0,1 olan sorular aşağıdakilerden hangileridir?
1) Bilgisayar kelimesinden rastgele bir harf seçilirse, bu harfin ünsüz olma olasılığı nedir?
2) İki madeni para havaya atıldığında, ikisini de tura gelme olasılığı nedir?
3) Adnan rastgele üç basamaklı sayıyı seçer. Bu sayının son rakamı 6 olma olasılığı bulunuz.
4) Ortalamada 100 adet cep feneri başına 7 tane arızalı denk gelmektedir. Çalışan feneri satın alma
olasılığı bulunuz.
5) Taksi firmasında şu anda 10 araç boştur: 5 siyah, 1 sarı ve 4 yeşil. Taksi dırağına yapılam çağrı
yapılması durumunda ,müşteriye tesadüfen en yakın bulunan araçlardan birinin sarı renk taksi olma
olasılığını bulun.
6) Timur ile babası ile dönme dolaba binmeye karar verirler. Dönme dolapta toplam 10 kabin vardır: 1 mavi, 8 yeşil, kalanlar kırmızı. Kabinler sıra ile binme platformuna gelmektedir. Timur'un kırmızı kabine
binme olasılığını bulunuz.
2.Bölüm. 6.-10.sorular. Her soru 5 puan değerindedir.
6. - 8.sorularda uygun eşleştirmeleri yapınız. Eşleştirdiğiniz rakam ve harfi cevaplar tablosuna
örnekteki gibi yazınız. ÖRNEK:
1
A 2 C 3 B 4 D 5 E
6. İfadelerin değerlerini bularak uygun eşleştirmeleri yapınız:
İfadeler
2 3
1)( 49 ·4 ):196
A) 121
2) (48·1110):448
B) 784
8 11
7
3) (3 ·4 ):12
C) 196
4) (47·497):1966
D) 27
9
12
9
E) 768
5) (49 ·3 ):147
Değerler
7. Aşağıdaki problemleri, doğru cevapları ile eşleştiriniz:
Soru
1) Veysel ile aynı yaşta olan erkek çocukların ortalama ağırlığı 54 kg. Veysel
ortalamadan %35 fazla olduğuna göre, Veysel kaç kilogramdır?
2)Bütçesi 40 milyon ruble bir firmada, bütçenin %25 ini oluşturan bir harcama için kaç
ruble harcanır?
3) Açık arttırmada ürünün fiyatı %50 düşürüldükten sonra 940 ruble olmuştur. Açık
arttırmadan önce ürünün fiyatı ne kadardı?
4) Yılın başında 200 bin kişi olan "Batı" telefon şirketin abone sayısı, yılın sonunda 230
bin kişi olmuştur. Bu şirketin abone sayısı bir yılda yüzde kaç artmıştır?
5) Vişnenin bir kilosunun fiyatı 120 ruble, kirazın ise 150 rubledir. Vişnenin fiyatı,
kirazdan yüzde kaç ucuzdur?
8. Aşağıdaki problemleri, doğru cevapları ile eşleştiriniz:
Soru
1) Nilay'ın cep telefonunda 56 kontör vardı, Sevgi ile konuştuktan sonra 21 kontörü kaldı. Konuşmanın bir
dakikası 2,50 kontör olduğuna göre Sevgi ile konuşması kaç dakika sürmüştür?
2) 11"A" sınıfının mezunları, mezuniyet töreni için öğretmenlerine, rehber öğretmenine ve okul müdürüne
buket çiçek verecektir.Her öğretmen için bukette 5 gül, rehber öğretmen ve okul müdürü için ise 9 gül
planlamışlardır. Mezunlar, 17 öğretmene (okul müdürü ve rehber öğretmen dahil) buket hediye
edeceklerdir. Güllerin tanesi 30 rubleden toptan fiyatına alınmaktadır. Tüm güllerin fiyatı kaç paradır?
3) Elektrik sayacın göstergesii 1 Kasım tarihinde 7061 kW-saat, 1 Aralık tarihinde ise 7249 kW-saat
göstermektedir. Elektrik enerjinin 1 kW-saati 1 TL 10 kuruş olduğuna göre Kasım ayı elektrik parası ne
kadardır? Cevabı TL olarak veriniz.
4) Döviz bürosunda 1 Grivna'nın bedeli 4 TL 10 kuruştur. 1 kg’ı 11 Grivna olan portakaldan 7 kg
alınduğında,bu alışverişin kaç TL'ye karşılık geldiğini bulunuz, Cevabı tam sayıya yuvarlayınız.
5) Özge 14 arkadaşına yılbaşı tebrikleri içeren SMS göndermiştir. Bir SMS fiyatı 1 TL 30 kurutur. SMS
göndermeden önce Özge’nin hesabında 77 lira vardı. Tüm SMS gönderildikten sonra Özge'de kaç lira
kalacaktır?
Cevap
A) 20
B) 15
C) 72,9
D) 1.880
E) 10 000 000
Cevap
A) 206,8
B) 14
C) 2790
D) 58,8
E) 316
9.-10.sorularda uygun sıralamaları yapınız. Yaptığınız sıralamayı cevaplar tablosuna örnekteki gibi
yazınız. ÖRNEK:
1
3 5 2 4
9. Tabloda Türkiye'nin beş şehrinde (2010 yılın başı itibariyle) bazı esas gıda ürünleri için ortalama
fiyatları (TL olarak) belirtilmiştir. Her şehir için, 3 buğday ekmek, 3 kg patates, l ayçiçek yağıdan oluşan
gıda ürünleri setinin fiyatını (TL olarak) belirleyiniz ve küçükten büyüğe doğru sıralayınız:
Gıda adı
1) Niğde 2) Kayseri
3) Edirne
4) Kastamonu 5) Kemer
Buğday ekmek
13
10
16
11
14
Süt (1 litre)
25
21
27
26
23
Patates (1 kg)
9
13
16
17
12
Peynir (1 kg)
260
220
270
240
265
Et (dana eti, 1 kg)
280
240
300
285
280
Ay çiçek yağı (1 litre)
38
44
50
52
44
10. Dik kenarları 12 ve 5 olan dik açılı üçgen verilmiştir. Üçgenin hipotenüsünü, alanını ve yarı
çevresini, ayrıca iç teğet çemberin yarıçapını ve çevrel çemberin yarıçapını bulunuz. Sonuçları küçükten
büyüğe doğru sıralayınız.
3.Bölüm. 11.-15.sorular. Her soru 8 puan değerindedir.
11. - 12.sorularda uygun eşleştirmeleri yapınız. Eşleştirdiğiniz rakam ve harfi cevaplar tablosuna
örnekteki gibi yazınız. ÖRNEK:
1 A 2 C 3 D 4 B
11. Diyagramda, yıl içinde bir beyaz eşya mağazasında aylık buzdolabı satış durumu gösterilmiştir.
Diyagramı kullanarak belirtilen zaman periyotları içinde ürünlerin satış durumları ile eşleştiriniz:
1) yılın ilk çeyreği
2) yılın 2. Çeyreği
3) yılın 3. Çeyreği
4) yılın 4. Çeyreği
A) en hızlı satış artışı
B) iki ay aynı, sonra artmış
C) minimum satış hacmi
D) maksimum satış hacmi
12. Fonksiyonlar ile tanım kümelerini eşleştiriniz:
1) у  ( 2  х )5
А)  ;3 
2) у  ( 8  2 х )
3) у  4  2 х
4) у 
1
9  3х
6
B)  ;4   4; 
C)  ; 
D)  ;2
13. - 14.sorularda uygun sıralamaları yapınız. Yaptığınız sıralamayı cevaplar tablosuna örnekteki
gibi yazınız. ÖRNEK:
1
3 4 2
13. Aşağıdaki soruların cevapları bularak bulduğunuz değerleri küçükten büyüğe doğru sıralayınız:
1) ABC üçgeninde C açısı 90∘, CH – yükseklik, AC = 25, AH = 15 ise cos B =?
2) ABC üçgeninde C açısı 90∘, CH – yükseklik, BC = 25, CH = 24 ise sin A =?
3) ABC üçgeninde C açısı 90∘, CH – yükseklik, AH = 15, tgA = 3/5 ise |BH|=?
4) ABC üçgende AC = BC, AB = 30, sinA = 0,8 ise |AC|=?
14. Soruların cevaplarını bularak değerleri büyükten küçüğe doğru sıralayınız:
1) g= 9,8, m = 5, E = 4,9 ise E = mgh eşitlikte h=?, bulunuz.
2) p1, p2, p3 – asal sayılar ise, p1∙p2∙p3 sayının tüm bölenlerin toplamı (p1+1)∙(p2+1)∙(p3+1) ise 154 sayısının
bölenlerin toplamını bulunuz.
3) ayrıtları a,b,c olan dikdörtgenler prizmasının yüzey alanı S = 2·(ab + ac + bc) formülüne göre
hesaplanır. Kenarları 2,4,6 olan dikdörtgenler prizmasının yüzey alanını bulunuz.
4) a,b,c üç sayıların geometrik ortalaması g  3 abc formülüne göre hesaplanmaktadır. 2,6,144 sayıların
geometrik ortalama değerini hesaplayınız.
15.soruda 4 alt soru vardır. Her sorunun bir doğru cevabı vardır. Doğru cevabın numarasını
cevaplar tablosuna yazınız.
15. Verilen aralıkta y = x-4 fonksiyonun en büyük değerini bulunuz:
15.1. [0,5; 1]
15.2. (–∞;–2]
15.3. (–3; –1]
1) 1
1) 1
1) 1
2) 1/81
2) 1/81
2) 1/81
3) 1/16
3) 1/16
3) 1/16
4) 16
4) 16
4) 16
15.4. [3; +∞)
1) 1
2) 1/81
3) 1/16
4) 16
4.Bölüm. 16.soru 20 puan değerindedir.
16.soruda 4 alt soru vardır ve her alt soru 5 puan değerindedir. Cevabı, her kare içine bir rakam
gelecek şekilde boşluk bırakmadan yazınız. Ondalık kesri yazabilmek için virgül işareti kullanınız.
16.1. ( х 2  4 ) х 2  х  20  0 denklemin en büyük kökünü bulunuz ve cevap tablosuna yazınız.
16.2. ( х 2  4 ) х 2  х  20  0 denklemin kök toplamını bulunuz ve değerini cevap tablosuna yazınız.
16.3. ( х 2  4 ) х 2  х  20  0 denklemin köklerin aritmetik ortalama değerini bulunuz ve değerini cevap
tablosuna yazınız.
16.4. ( х 2  4 ) х 2  х  20  0 denklemin en küçük kökünü bulunuz ve cevap tablosuna yazınız.