ÖLÜ M 2 - WordPress.com

BÖLÜM
2
L İNEER S İSTEMLER
Genel durumda diferansiyel denklemlerin çözümlerini açık olarak elde etmek veya çözümlerin
bazı önemli özelliklerini araştırmak için genel yöntemler yoktur, çoğu zaman denkleme özel yöntemler geliştirmek gereklidir. Fakat lineer durumda çözümlerin en temel özellikleri için kapsamlı
bir teori mevcuttur, hatta sabit katsayılı durumda denklemin veye sistemin çözümü açık olarak
elde edilebilir. Bu bölümde lineer diferansiyel denklem sistemlerinin çözümlerinin elde edeceğimiz bazı temel özellikleri, lineer olmayan sistemler için de temel oluşturur.
2.1 Giriş
Şimdi x(t ) := (x 1 (t ), x 2 (t ), . . . , x n (t ))T bilinmeyen bir vektörel fonksiyon, i , j = 1, 2, . . . , n olmak üzere
a i j (t ) ve b i (t ) fonksiyonları da (r 1 , r 2 ) aralığında verilmiş sürekli fonksiyonlar olmak üzere, birinci
mertebeden n°boyutlu
x i0 =
n
X
j =1
a i j (t )x j + b i (t ),
i = 1, 2, . . . , n
(2.1.1)
°
¢
lineer sistemini ele alalım. Eğer A(t ) ile n£n boyutlu a i j (t ) matrisini, B (t ) ile de (b 1 (t ), b 2 (t ), . . . , b m (t ))T
vektörünü gösterirsek (2.1.1) sistemini
x 0 = A(t )x + B (t )
(2.1.2)
olarak ifade edebiliriz. A ve B matrisleri kapalı bir bölgede sürekli ise f (t , x) := A(t )x +B (t ) fonksiyonunun her iki değişkene göre türevleri sürekli olacaktır, dolayısıyla bu bölgede Lipschitz koşulu
sağlanır. Böylece Teorem 1.2.24 gereği A(t ) ve B (t ) matrislerinin sürekli sürekli olduğu kapalı bir
bölgede (2.1.2) denklemi ile verilen bir başlangıç değer probleminin tek bir çözümü vardır.
(2.1.2) tipindeki lineer denklemlerin önemli bir özelliği süperpozisyon ilkesi denilen şu özelliktir. x 1 (t ) fonksiyonu (2.1.2) sisteminin B (t ) = B 1 (t ) için bir çözümü, x 2 (t ) fonksiyonu da aynı
sistemin B (t ) = B 2 (t ) için bir çözümü olsun. Bu durumda c 1 ve c 2 verilmiş skaler sabitler olmak
üzere x(t ) = c 1 x 1 (t )+c 2 x 2 (t ) fonksiyonu (2.1.2) sisteminin B (t ) = c 1 B 1 (t )+c 2 B 2 (t ) için bir çözümü
33
Bölüm 2. Lı̇neer Sı̇stemler
34
olur. Gerçekten bunu
x 0 (t )
=
c 1 x 10 (t ) + c 2 x 20 (t )
=
A(t ) (c 1 x 1 (t ) + c 2 x 2 (t )) + c 1 B 1 (t ) + c 2 B 2 (t )
=
=
c 1 (A(t )x 1 (t ) + B 1 (t )) + c 2 (A(t )x 2 (t ) + B 2 (t ))
A(t )x(t ) + B (t )
olarak gözlemleyebiliriz. Özel olarak x 1 (t ) ve x 2 (t ) fonksiyonları aynı
x 0 = A(t )x
(2.1.3)
lineer homojen sisteminin çözmleri iseler, bu durumda x(t ) = c 1 x 1 (t )+c 2 x(t ) fonksiyonu da (2.1.3)
sisteminin bir çözümü olur. Dahası, eğer x 1 (t ) fonksiyonu (2.1.2) sisteminin bir çözümü ise, x 2 (t )
fonksiyonunun da (2.1.2) sisteminin bir çözümü olması için gerek ve yeter koşul x 1 (t )°x 2 (t ) fonksiyonunun (2.1.3) sisteminin bir çözümü olmasıdır.
Süperpozisyon ilkesi daha soyut bir biçimde şöyle de ifade edilebilir. B (t ) fonksiyonu bir L
vektör uzayının elemanlarını tarasın, ayrıca her B (t ) 2 L için (2.1.2) sisteminin tek bir çözümü
olsun. Bu durumda (2.1.2) sisteminin çözümlerinin kümesi olan Y kümesi bir vektör uzayıdır.
Lineer sistemlerin kalitatif özelliklerinin araştırılmasında matrisler teorisi çok önemlidir. Şimdi
matrislerle ilgili ihtiyacımız olacak bazı bilgileri özetleyelim. Okuyucu bu bilgileri lineer cebir
derslerinden
Sadece elemanları reel değerli olan kare matrislerle ilgileneceğiz.
° hatırlayacaktır.
¢
Bir A = a i j matrisinin normunu tüm elemanlarının mutlak değerce toplamı olarak, yani
kAk :=
n Ø
X
Ø
Øa i j Ø
(2.1.4)
i , j =1
olarak tanımlarız. Matrislerin bir {A n } dizisi, eğer n ! 1 için kA n ° Ak ! 0 ise, A matrisine yakınsaktır denir. Ayrıca Cauchy yakınsaklık kriteri matrisler için de geçerlidir. Matrislerin bir serisinin
kısmi toplamlar dizisi yakınsak ise ilgili seri de yakınsaktır. Bir A matrisinin determinantını det A
veya |A| ile, transpozunu A T ile, ve izinin (esas köşegen üzerindeki elemanları toplamını) Tr A ile
göstereceğiz. Bir A matrisisnin terslenebilir olması için gerek ve yeter koşul det A 6= 0 olmasıdır. I
ile n°boyutlu birim matrisi gösterelim, n £n boyutlu bir A kare matrisi için ∏ değişkeninin n°inci
dereceden
f (∏) = det (A ° ∏I )
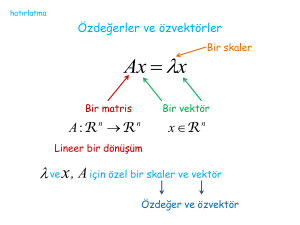
polinomuna A matrsinin karakteristik polinomu, bu polinomun köklerine de bu matrisin özdeğerleri denir. Tüm özdeğerlerinin çarpımının det A değerine, toplamının da Tr A değerine eşit olduğu kolayca doğrulanabilir. Bir ∏0 özdeğeri için Ax 0 = ∏0 x 0 eşitliğini sağlayan sıfırdan farklı x 0
vektörüne, A matrisinin ∏0 özdeğerine karşılık gelen öz vektörü denir.
A ve B iki matris olsun. Eğer A = T °1 BT eşitliği sağlanacak şekilde bir terslenebilir T matrisi
varsa, A ile B matrislerine benzer matrisler denir. Benzer matrislerin karakteristik polinomlarının
aynı olduğu kolayca doğrulanabilir.
Bir A kare matrisinin Jordan kanonik biçimi ile ilgili aşağıdaki temel sonucu hatırlayalım.
Teorem 2.1.1 k 1 + k 2 + · · · + k r = n olmak üzere ∏1 , ∏2 , . . . , ∏r sayıları n £ n boyutlu A matrisinin
k 1 , k 2 , . . . , k r katlı özdeğerleri olsun. Bu durumda L 1 (∏ j ) := ∏ j ve
0
B
B
L k j (∏ j ) := B
B
@
∏j
0
..
.
0
1
∏j
..
.
0
0
1
..
.
0
···
···
···
0
0
∏j
0
1
0
0 C
C
C
C
1 A
∏j
Yrd. Doç. Dr. Süleyman ÖĞREKÇİ
2.1. Giriş
35
olmak üzere
T
°1
0
B
B
AT = B
B
@
L k1 (∏1 )
0
..
.
0
0
L k2 (∏2 )
..
.
0
···
···
···
1
0
0
..
.
L kr (∏r )
C
C
C
C
A
olacak şekilde terslenebilir bir T matrisi vardır. Özel olarak eğer A matrisinin tüm özdeğerleri farklı
ise
0
1
∏1 0 · · · 0
B 0 ∏
··· 0 C
B
C
2
°1
T AT = B
..
.. C
B ..
C
@ .
.
. A
0
0
···
olacak şekilde terslenebilir bir T matrisi vardır.
∏n
Örnek 2.1.2 6 £ 6 boyutlu bir A matrisinin özdeğerleri ∏1 = ∏2 = 1, ∏3 = ∏4 = ∏5 = 6 ve ∏6 = 3
biçiminde olsun. Bu durumda r = 3, k 1 = 2, k 2 = 3, k 3 = 1 ve
0
1
µ
∂
6 1 0
1 1
L 2 (1) =
, L 3 (6) = @ 0 6 1 A , L 1 (3) = 3
0 1
0 0 6
biçimindedir. Dolayısıyla
0
B
B
B
B
B
T °1 AT = B
B
B
B
@
1
0
1
1
0
0
1
0 C 0
C
C B
C B
C B
C=B
0 C
C @
C
A
0
6
0
0
1
6
0
0
1
6
0
1
0
0
0
0
1
0
0
0
0
0
6
0
0
0
0
1
6
0
0
0
0
1
6
0
0
0
0
0
3
3
olacak şekilde bir T matrisi vardır.
1
C
C
C
C
A
⇤
Şimdi de kompleks özdeğerler bulunması durumunu ele alalım. A n£n matrisinin ∏1 , ∏2 , . . . , ∏r
özdeğerleri reel, u 1 , u 2 , . . . , u m özdeğerleri de kompleks olsun. Bu kompleks özdeğerler u i = u i °1
biçiminde olsun. Bu durumda r + m = n olacaktır. Æk ve Øk sayıları
u k°1 = Æk°1 + i Øk°1
eşitliğini sağlayan sayılar olsun. Bu durumda
0
∏1 0 · · · 0
B
0 ∏2 · · · 0
B
B
..
..
..
B
B
.
.
.
B
B
0
0
·
·
·
∏
r
B
B
B
T °1 AT = B
B
0
B
B
B
B
B
0
B
B
@
..
.
olacak şekilde bir T matrisi vardır.
ve
u k = Æk°1 ° i Øk°1
0
Æ1
°Ø1
Ø1
Æ1
0
..
.
0
0
0
0
Æ2
°Ø2
Ø2
Æ2
..
.
0
1
C
C
··· C
C
C
C
C
C
C
C
C
··· C
C
C
C
C
··· C
C
C
A
..
.
Bölüm 2. Lı̇neer Sı̇stemler
36
Örnek 2.1.3
0
°1
@
0
A=
0
1
°1
9 A
°2
1
°2
1
olsun. Bu durumda det(A ° ∏I ) = °(∏ + 1)(∏2 + 4∏ + 13) olup özdeğerler
∏1 = °1,
u 1 = °2 + 3i ,
olarak tespit edilir. Böylece
olacak şekilde bir T matrisi vardır.
0
u 2 = °2 ° 3i
0
°2
°3
°1
°1
@
0
T AT =
0
1
0
3 A
°2
⇤
Uyarı 2.1.4 İki boyutlu lineer sistemler için Jordan kanonik formları özetleyelim.
(i) A 2£2 matrisinin farklı iki ∏ ve µ özdeğeri varsa
µ
∏
°1
T AT =
0
0
µ
∂
olacak şekilde bir T matrisi vardır.
(ii) A 2£2 matrisinin çift katlı bir ∏ özdeğeri varsa, bu özdeğere karşılık gelen öz vektörlerin lineer
bağımsız veya bağımlı olması durumuna karşılık sırasıyla
µ
∂
µ
∂
∏ 0
∏ 1
°1
°1
T AT =
veya T AT =
0 ∏
0 ∏
olacak şekilde bir T matrisi vardır.
(iii) A 2£2 matrisinin özdeğerleri Æ ± i Ø ise
T °1 AT =
µ
Æ
°Ø
Ø
Æ
∂
olacak şekilde bir T matrisi vardır.
Œ
2.2 Çözümler ve Temel Özellikleri
Homojen Denklemler
Bu
x(t ) := (x 1 (t ), x 2 (t ), . . . , x n (t ))T bilinmeyen n°boyutlu bir vektörel fonksiyon ve A :=
° bölümde
¢
a i j de (r 1 , r 2 ) aralığında verilen sürekli n £ n boyutlu bir matris fonksiyonu olmak üzere
x 0 = A(t )x
(2.2.1)
lineer homojen denklem sisteminin çözümlerinin temel özelliklerini araştıracağız.
(2.2.1) denkleminin çözümlerinin herhangi bir kombinasyonu yine (2.2.1) denkleminin bir
çözümü olur. j = 1, 2, . . . , n olmak üzere ¡ j (t ) fonksiyonları (2.2.1) denkleminin çözümleri ve c j ’ler
de keyfi sabitler olsun. Ayrıca
n
X
¡(t ) :=
c j ¡ j (t )
j =1
Yrd. Doç. Dr. Süleyman ÖĞREKÇİ
2.2. Çözümler ve Temel Özellikleri
37
fonksiyonunu tanımlayalım. Buradan türev alarak
¡0 (t ) =
n
X
j =1
c j ¡0j (t ) =
n
X
j =1
n
X
°
¢
c j A(t )¡ j (t ) = A(t )
c j ¡ j (t ) = A(t )¡(t )
j =1
elde ederiz ki bu da ¡(t ) fonksiyonunun (2.2.1) denkleminin bir çözümü olduğunu gösterir.
Dikkat edilmelidir ki ¡(t ) ¥ 0 fonksiyonu (r 1 , r 2 ) aralığında (2.2.1) denkleminin bir çözümüdür.
Hatta aşağıda kanıtlayacağımız gibi bu çözüm (2.2.1) denkleminin ¡(t 0 ) = 0 koşulunu sağlayan
tek çözümüdür.
Lemma 2.2.1 t 0 2 (r 1 , r 2 ) ve ¡(t ) fonksiyonu (2.2.1) denkleminin ¡(t 0 ) = 0 koşulunu sağlayan çözümü olsun. Bu durumda t 2 (r 1 , r 2 ) için ¡(t ) ¥ 0 olur.
İspat ¡(t ) ¥ 0 fonksiyonu (r 1 , r 2 ) aralığında (2.2.1) denklemini ve ¡(t 0 ) = 0 başlangıç koşulunu
sağlar. Çözümün tekliği gereği bundan başka çözüm yoktur.
Á
v 1 (t ), v 2 (t ), . . . , v n (t ) fonksiyonları bir I aralığında tanımlı olsunlar. Her t 2 I için
n
X
i =1
c i v i (t ) = 0
eşitliği sadece c 1 = c 2 = · · · = c n = 0 için sağlanıyorsa bu v i (t ) fonksiyonları I aralığında lineer
bağımsızdır denir. Aksi taktirde bu fonksiyonlar lineer bağımlıdır.
Teorem 2.2.2 ¡1 (t ), ©2 (t ), . . . , ¡n (t ) fonksiyonları (r 1 , r 2 ) aralığında (2.2.1) denkleminin lineer bağımsız çözümleri olsunlar. Bu durumda
n
X
c j ¡ j (t )
j =1
lineer kombinasyonu c 1 = · · · = c n = 0 olmadıkça (r 1 , r 2 ) aralığındaki hiç bir t için sıfır olmaz.
P
İspat ¡(t ) := nj=1 c j ¡ j (t ) tanımlayalım. Bu durumda denklem lineer olduğundan ¡(t ) fonksiyonu (2.2.1) denkleminin bir çözümü olur. Eğer bir t 0 2 (r 1 , r 2 ) için ¡(t 0 ) = 0 oluyorsa Lemma 2.2.1
gereği (r 1 , r 2 ) aralığında ¡(t ) ¥ 0 olur. Bu ise lineer bağımsızlıkla çelişir, o halde ¡(t ) fonskiyonu
(r 1 , r 2 ) aralığında hiçbir zaman sıfır olamaz.
Á
Tanım 2.2.3 (Temel çözüm) (2.2.1) denkleminin (r 1 , r 2 ) aralığındaki ¡1 (t ), ¡2 (t ), . . . , ¡n (t ) çözümleri eğer bu aralıkta lineer bağımsız iseler, bu durumda bu çözümlere (2.2.1) denkleminin bir temel
çözümler sistemi denir.
Teorem 2.2.4 (2.2.1) denkleminin bir temel çözümler sistemi her zaman vardır.
İspat ¡1 (t ), ¡2 (t ), . . . , ¡n (t ) fonksiyonları (r 1 , r 2 ) aralığında (2.2.1) denkleminin
¡ j (t 0 ) = e j ,
j = 1, 2, . . . , n
başlangıç koşullarını sağlayan çözümleri olsunlar. Burada t 0 2 (r 1 , r 2 ) ve e j ler de Rn in birim vektörleridir. Çözümün tekliği gereği, bu çözümler farklı başlangıç koşullarını sağladıklarından, birbirlerinden farklıdırlar. Bu çözümlerin (r 1 , r 2 ) aralığında lineer bağımsız olduklarını iddia ediyoruz. Varsayalım ki bu yanlış olsun, bu durumda hepsi birden sıfır olmayan c j sabitleri için
¡(t ) :=
n
X
j =1
c j ¡ j (t ) ¥ 0,
t 2 (r 1 , r 2 )
Bölüm 2. Lı̇neer Sı̇stemler
38
olur. Böylece
¡(t 0 ) =
n
X
j =1
c j ¡ j (t 0 ) =
n
X
j =1
c j e j = (c 1 , c 2 , . . . , c n ) = 0
elde ederiz. Buradan c 1 = c 2 = · · · = c n = 0 elde edilir ki bu da fonksiyonların lineer bağımsız olmasıyla çelişir.
Á
Sonuç 2.2.5 (2.2.1) denkleminin her çözümü, temel çözümler sisteminin elemanlarının bir lineer
kombinasyonu olarak yazılabilir.
İspat t 0 2 (r 1 , r 2 ) olmak üzere x(t ) fonksiyonu (r 1 , r 2 ) aralığında (2.2.1) denkleminin x(t 0 ) = x 0 :=
(x 10 , x 20 , . . . , x n0 )T başlangıç koşulunu sağlayan çözümü olsun. Ayrıca j = 1, 2, . . . , n olmak üzere
¡ j (t ) fonksiyonları da (2.2.1) denkleminin ¡ j (t 0 ) = e j koşullarını sağlayan bir temel çözümler
sistemi olsun. Şimdi
n
X
¡(t ) :=
x j 0 ¡ j (t )
j =1
olarak tanımlarsak ¡(t ) fonksiyonunun (2.2.1) denklemini sağladığı açıktır. Ayrıca
¡(t 0 ) =
n
X
j =1
x j 0 e j = (x 10 , x 20 , . . . , x n0 ) = x 0
olur. Çözümün tekliği gereği böylece t 2 (r 1 , r 2 ) için ¡(t ) ¥ x(t ) elde edilmiş olur.
Á
Uyarı 2.2.6 Elde ettiğimiz bu sonuçlar bize (2.2.1) denkleminin tüm çözümlerinin n°boyutlu bir
vektör uzayı oluşturduğunu gösterir. (2.2.1) denkleminin her çözümü temel çözümler cinsinden
yazılabildiği için bu denklemin çözümlerinin özelliklerini araştırmak için sadece n°tane temel
çözümünü ele almak yeterlidir. Œ
°
Şimdi j °inci sütunu (2.2.1) denkleminin ¡ j (t 0 ) = e j koşulunu sağlayan çözümü ¡ j (t ) := ¡1 j ,
¢T
¡2 j , . . . , ¡n j vektörü biçiminde olan n £ n matrisini ©(t ) ile gösterelim. Yani
0
¡11 (t )
B
..
©(t ) := @
.
¡n1 (t )
···
···
¡1 j (t )
..
.
¡n j (t )
···
···
olarak tanımlayalım. ©(t 0 ) = I eşitliğinin sağlandığı açıktır.
1
¡1n (t )
C
..
A
.
¡nn (t )
Sonuç 2.2.7 Yukarıda tanımlanan ©(t ) matrisi
©0 (t ) = A(t )©(t )
(2.2.2)
matris diferansiyel denklemini ve ©(t 0 ) = I eşitliğini sağlar. Ayrıca (2.2.1) denkleminin x(t 0 ) = x 0
başlangıç koşulunu sağlayan x(t ) çözümü x(t ) = ©(t )x 0 eşitliğini sağlar.
İspat Her ¡ j (t ) sütunu (2.2.1) denkleminin bir çözümü olduğundan her j = 1, 2, . . . , n için ¡0j (t ) =
A(t )¡ j (t ) eşitliği sağlanır. Bu da (2.2.2) eşitliğinin sağlandığını gösterir. Şimdi x 0 := (x 10 , x 20 , . . . , x n0 )T
olsun. Bu durumda Sonuç 2.2.5 gereği
x(t ) =
n
X
x j 0 ¡ j (t )
j =1
eşitliği sağlanır. Bu eşitliğin sağ tarafı ©(t )x 0 matris çarpımı olduğundan x(t ) = ©(t )x 0 eşitliği elde
edilmiş olur.
Á
Yrd. Doç. Dr. Süleyman ÖĞREKÇİ
2.2. Çözümler ve Temel Özellikleri
39
Tanım 2.2.8 (Wronskian) Sütunları (2.2.1) denkleminin ¡1 (t ), . . . , ¡n (t ) çözümlerinden oluşan ©(t )
matrisinin determinantı olan skaler W (t ) := det ©(t ) fonksiyonuna ¡1 (t ), . . . , ¡n (t ) fonksiyonlarının Wronskianı denir.
Tanım 2.2.9 (Temel matris) Sütunları (2.2.1) denkleminin lineer bağımsız olan ¡1 (t ), . . . , ¡n (t )
çözümlerinden oluşan ©(t ) matrisine (2.2.1) denkleminin bir temel matrisi denir.
Teorem 2.2.10 (Abel-Liouville formülü) ©(t ) matrisi (2.2.1) denkleminin bir temel matrisi ve t 0 2
(r 1 , r 2 ) olsun. Bu durumda
∑Zt
∏
W (t ) = W (t 0 ) exp
Tr A(s) ds ,
t 2 (r 1 , r 2 )
t0
eşitliği sağlanır.
İspat W (t ) = det ©(t ) fonksiyonunun türevini hesaplamak için Jacobi türev formülü olarak bilinen formülü kullanacağız. Bu formüle göre herhangi bir ©(t ) kare matrisi için
µ
∂
d
d
det ©(t ) = Tr adj ©(t ) · ©(t )
dt
dt
eşitliği geçerlidir. Burada ©(t ) matrisinin sütunları lineer bağımsız olduğundan bu matris terslenebilirdir, dolayısıyla bu eşitlikte
adj ©(t )
©°1 (t ) =
det ©(t )
eşitliğini kullanarak
µ
∂
d
d
°1
det ©(t ) = Tr © (t ) · det ©(t ) · ©(t )
dt
dt
°
¢
eşitliğini elde ederiz. Diğer yandan Sonuç 2.2.7 gereği ©(t ) matrisi A(t ) = a i j (t ) olmak üzere ©0 =
A(t )© eşitliğini sağlar. Bunu da yukarıdaki eşitlikte kullanarak ve gerekli düzenlemeleri yaparak
°
¢
d
det ©(t ) = Tr ©°1 (t ) · det ©(t ) · A(t )©(t ) = Tr (det ©(t ) · A(t )) = det ©(t ) · Tr (A(t ))
dt
eşitliğine, yani
W 0 (t ) = Tr (A(t )) · W (t )
skaler diferansiyel denklemine varırız ki bu da ispatı tamamlar.
Á
Üstel fonksiyon hiç bir zaman sıfır olmadığından bu sonuçtan, eğer bir t 0 2 (r 1 , r 2 ) için W (t 0 ) =
0 oluyosa bu durumda her t 2 (r 1 , r 2 ) için W (t ) = 0 olacağını anlıyoruz. Aşağıda daha genel bir
sonuç elde edeceğiz.
Teorem 2.2.11 (2.2.2) denkleminin çözümü olan bir ©(t ) matrisinin (2.2.1) denkleminin bir temel
matrisi olması için gerek ve yeter koşul
W (t ) 6= 0,
t 2 (r 2 , r 2 )
olmasıdır.
İspat Sütunları (2.2.1) denkleminin çözümleri olan ¡ j (t ) vektörlerinden oluşan ©(t ) matrisi (2.2.1)
denkleminin bir temel matrisi olsun. Şimdi ¡(t ) fonksiyonu (2.2.1) denkleminin herhangi bir çözümü olsun, bu durumda
n
X
¡(t ) =
c j ¡ j (t )
j =1
Bölüm 2. Lı̇neer Sı̇stemler
40
olacak şekilde aynı anda hepsi sıfır olmayan c j sabitleri vardır. (2.2.1) denkleminin çözümlerinin
tekliği gereği ayrıca bu sabitler tektir. Eğer c := (c 1 , c 2 , . . . , c n )T olarak tanımlarsak bu eşitliği
¡(t ) = ©(t )c
biçiminde yazabiliriz. Her t 2 (r 1 , r 2 ) için bu eşitlik n°tane c 1 , . . . , c n bilinmeyenlerinin bir lineer
denklem sistemini belirtir ve çözüm tektir. Dolayısıyla ©(t ) matrisinin determinantı sıfırdan farklıdır.
Diğer taraftan, eğer t 2 (r 1 , r 2 ) için W (t ) 6= 0 ise bu aralıkta ¡ j (t ) sütun vektörleri lineer bağımsızdır. Bu vektörler (2.2.1) denkleminin çözümleri olduklarından ©(t ) matrisi bir temel matristir.
Á
Uyarı 2.2.12 Herhangi bir matrisin determinantı, sütunları lineer bağımsız olsa bile, sıfır olabilir.
Örneğin
0
1
1 t2 t4
©(t ) = @ 0 et e°t A
0 0 0
matrisinin determinantı sıfırdır ve sütunları herhangi bir aralıkta lineer bağımsızdır. Bu sütunlar
aynı lineer denklemin çözümleri olmadıklarından bu durum Teorem 2.2.11 sonucu ile çelişmez.
Œ
Örnek 2.2.13 (İkinci mertebeden lineer denklemler) p(t ) ve q(t ) fonksiyonları (r 1 , r 2 ) aralığında
sürekli olsunlar. Eğer y 1 (t ) ve y 2 (t ) fonksiyonları bu aralıkta
y 00 + p(t )y 0 + q(t )y = 0
(2.2.3)
denkleminin
W12 (y 1 , y 2 ) = y 1 y 20 ° y 10 y 2 6= 0,
t 2 (r 1 , r 2 )
koşulunu sağlayan çözümleri iseler, bu durumda diğer çözümlerin de bu iki çözümün lineer kombinasyonundan oluştuğunu kanıtladık. Şimdi bu denklem üzerinde bu durumu gözlemleyeceğiz.
Bir y 3 (t ) fonksiyonu (2.2.3) denkleminin bir çözümü olsun. Bu durumda
y 100 + p(t )y 10 + q(t )y 1 = 0
y 200 + p(t )y 20 + q(t )y 2 = 0
y 300 + p(t )y 30 + q(t )y 3 = 0
eşitlikleri sağlanır. İlk eşitliği °y 2 ile ve ikinci eşitliği y 1 ile çarpıp toplarsak
denklemine, yani
°
¢
y 1 y 200 ° y 100 y 2 + p(t ) y 1 y 20 ° y 10 y 2 = 0
0
W12
+ p(t )W12 = 0
denklemine ulaşırız. Buradan da
∑ Zt
∏
W12 (t ) = k 12 exp °
p(s) ds
elde ederiz, k 12 6= 0 olduğu açıktır. Benzer şekilde
£ Rt
§
°y 20 y 3 + y 2 y 30 = W23 (t ) = k 23 exp ° p(s) ds
£ Rt
§
°y 10 y 3 + y 1 y 30 = W23 (t ) = k 13 exp ° p(s) ds
Yrd. Doç. Dr. Süleyman ÖĞREKÇİ
2.2. Çözümler ve Temel Özellikleri
41
eşitlikleri elde edilebilir. Bunlardan ilk eşitliği °y 1 ile, ikincisini de y 2 ile çarpıp toplarsak
∑ Zt
∏
°
¢
W12 (t )y 3 (t ) = °k 23 y 1 (t ) + k 13 y 2 (t ) exp °
p(s) ds
eşitliğine varırız, buradan da
y 3 (t ) = °
k 23
k 13
y 1 (t ) +
y 2 (t )
k 12
k 12
⇤
olduğu sonucuna varırız.
Teorem 2.2.14 © matrisi (2.2.1) denkleminin bir temel matrisi ve C de terslenebilir herhangi bir
matris olsun, bu durumda ©C matrisi de (2.2.1) denkleminin bir temel matrisi olur. Ayrıca (2.2.1)
denkleminin her temel matrisi bir terslenebilir C matrisi için ©C biçiminde yazılabilir.
İspat ©(t ) matrisi (2.2.1) denkleminin bir temel matrisi ise Sonuç 2.2.7 gereği
(©(t )C )0 = A(t ) (©(t )C )
eşitliği sağlanır ve dolayısıyla ©(t )C matrisi (2.2.2) denkleminin bir çözümü olur. Ayrıca
det(©C ) = det © · detC 6= 0
olduğundan ©C matrisi (2.2.1) denkleminin bir temel matrisi olur.
Şimdi (2.2.1) denkleminin herhangi iki ©1 ve ©2 temel matrisi için ©2 = ©1C olacak şekilde
terslenebilir bir C matrisinin var olduğunu gösterelim. ©°1
1 (t )©2 (t ) =: ™(t ) tanımlayalım, bu durumda ©2 = ©1 ™ eşitliği sağlanır. Bu eşitliğin türevini alarak ©02 = ©1 ™0 + ©01 ™ eşitliğini elde ederiz. Bu eşitlikte (2.2.2) denklemini kullanırsak A©2 = ©1 ™0 + A©1 ™ ve ©1 ™0 = 0 sonucuna varırız.
Dolayısıyla isteniln özelliklerde terslenebilir bir sabit C := ™ matrisi bulunmuş olur.
Á
Uyarı 2.2.15 Şu hususlara dikkat edilmelidir. Öncelikle yukarıdaki teoremin iddiası C © matrisi
için doğru değildir. Ayrıca iki farklı lineer homojen sistem aynı temel matrise sahip olamaz. Dolayısıyla © matrisi A matrisini belirler, bunun tersi doğru değildir. Œ
Uyarı 2.2.16 Yukarıdaki teorem bize ©(t 0 ) = I kısıtlamasının gerekli olmadığını, elde ettiğimiz
sonuçların herhangi bir başlangıç koşulu için de geçerli olduğunu gösterir. Çünkü C := ©°1 (t 0 )
seçersek ©1 (t ) := ©(t )C matrisi ©1 (t 0 ) = I koşulunu sağlayan bir temel matris olur. Œ
Mertebenin Düşürülmesi
Bir I := [a, b] aralığında n £ n boyutlu
x 0 = A(t )x
(2.2.4)
sisteminin lineer bağımsız r tane çözümü biliniyorsa, bunları kullanarak (2.2.4) problemini n ° r
boyutlu bir lineer sistemi çözme problemine indirgeyebiliriz. Şimdi bu indirgeme işlemini açıklayacağız.
Öncelikle (2.2.4) sisteminin bilinen lineer bağımsız r tane çözümünün oluşturduğu n £ r boyutlu matrisi X r (t ) ile gösterelim. Ayrıca aşağıdaki sekilde gösterildiği gibi X r (t ) matrisinin ilk r £r
boyutlu bloğunu X r 1 (t ) ile, kalan (n ° r ) £ r boyutlu bloğunu da X r 2 (t ) ile gösterelim.
0
B
B
X r (t ) := B
B
@
·
·
·
·
·
·
·
·
·
·
·
·
···
·
·
·
·
1
0
C B
C B
C=B
C B
A B
@
X r 1 (t )
X r 2 (t )
1
C
C
C
C
C
A
Bölüm 2. Lı̇neer Sı̇stemler
42
Şimdi I aralığının t 0 2 I 1 ve her t 2 I 1 için det X r 1 (t ) 6= 0 olacak şekilde bir I 1 := [Æ, Ø] alt aralığının var olduğunu varsayalım ve n £ n boyutlu Y (t ) matrisini
Y (t ) :=
µ
X r 1 (t )
X r 2 (t )
∂
0
I n°r
(2.2.5)
olarak tanımlayalım, bu durumda t 2 I 1 için det Y (t ) = det X r 1 (t ) 6= 0 olacaktır. Bu matrisin tersini
hesaplamak için bloklara ayırarak matris çarpımından faydalanarak
Y
°1
(t ) :=
µ
X r°1
(t )
1
°X r 2 (t )X r°1
(t )
1
0
I n°r
∂
(2.2.6)
elde ederiz. Ayrıca (2.2.5) eşitliğinde doğrudan türev alarak
0
Y (t ) := A(t )
µ
X r 1 (t )
X r 2 (t )
0
0
∂
(2.2.7)
eşitliğinin sağlandığı kolayca görülebilir.
Diğer yandan r £ r boyutlu A 11 (t ) matrisini, (n ° r ) £ (n ° r ) boyutlu A 22 (t ) matrisini ve diğer
A 12 (t ) ile A 21 (t ) matrislerini
µ
∂
A 11 (t ) A 12 (t )
A(t ) =
(2.2.8)
A 21 (t ) A 22 (t )
eşitliği ile tanımlayalım. Ayrıca r boyutlu y 1 vektörünü ve (n ° r ) boyutlu y 2 vektörünü de
y :=
µ
y1
y2
∂
(2.2.9)
olacak şekilde tanımlayalım.
Şimdi (2.2.4) sisteminde yeni bir y değişkeni için x = Y (t )y değişken dönüşümünü uygularsak
olduğundan
°
¢0
Y (t )y = A(t )Y (t )y
)
Y 0 (t )y + Y (t )y 0 = A(t )Y (t )y
£
§
y 0 = Y °1 (t ) A(t )Y (t ) ° Y 0 (t ) y
(2.2.10)
yeşitliğini elde ederiz. Eğer (2.2.5), (2.2.6), (2.2.7), (2.2.8) ve (2.2.9) ifadelerini (2.2.10) eşitliğinde
yerine yazarsak
0
A(t )Y (t ) ° Y (t )
=
=
=
=
=
=
A(t )Y (t ) ° A(t )
µ
X r 1 (t )
X r 2 (t )
0
0
∂∏
∂
∑
µ
X r 1 (t ) 0
A(t ) Y (t ) °
X r 2 (t ) 0
∑µ
∂ µ
X r 1 (t ) 0
X r 1 (t )
A(t )
°
X r 2 (t ) I n°r
X r 2 (t )
µ
∂
0
0
A(t )
0 I n°r
µ
∂µ
∂
A 11 (t ) A 12 (t )
0
0
A 21 (t ) A 22 (t )
0 I n°r
µ
∂
0 A 12 (t )
0 A 22 (t )
0
0
∂∏
Yrd. Doç. Dr. Süleyman ÖĞREKÇİ
2.2. Çözümler ve Temel Özellikleri
43
olduğundan
µ
y 10
y 20
∂
=
=
µ
µ
X r°1
(t )
1
°X r 2 (t )X r°1
(t )
1
0
I n°r
∂µ
0
0
A 12 (t )
A 22 (t )
∂µ
X r°1
(t )A 12 (t )
1
°X r 2 (t )X r°1
(t )A 12 (t ) + A 22 (t )
1
0
0
∂µ
y1
y2
y1
y2
∂
∂
eşitliğine, yani
y 10
y 20
X r°1
(t )A 12 (t )y 2
1
£
§
°X r 2 (t )X r°1
(t )A 12 (t ) + A 22 (t ) y 2
1
=
=
(2.2.11)
(2.2.12)
sistemine ulaşırız.
Dikkat edilirse (2.2.12) denklemi y 2 bilinmeyeninin (n°r )£(n°r ) boyutlu lineer bir sistemidir,
bunun çözümü elde edilebilirse (2.2.11) denkleminde yerine yazılarak bu denklemin de çözümü
elde edilir. Böylece n tane çözümün tamamı elde edilmiş olur. Unutulmamalıdır ki bu yöntem
sadece I 1 alt aralığında geçerlidir, tüm I aralığında değil.
Homojen Olmayan Denklemler
Şimdi n°boyutlu bilinmeyen bir x vektörü, verilen n £ n boyutlu ve (r 1 , r 2 ) aralığında sürekli bir
A(t ) matrisi ve aynı aralıkta sürekli olan verilmiş bir B (t ) n°boyutlu vektörü için
x 0 = A(t )x + B (t )
(2.2.13)
denklemini ele alalım. Bu denkleme n°inci mertebeden homojen olmayan lineer sistem denir. A
ve B sürekli olduğundan bu denklemin bir başlangıç değer probleminin tek çözümü vardır.
(2.2.1) ve (2.2.13) sistemleri arasında yakın ilişki vardır. Eğer (2.2.1) denkleminin bir temel
matrisi biliniyorsa, bu durumda (2.2.13) denkleminin çözümleri de bundan faydalınalarak elde
edilebilir.
Teorem 2.2.17 (Sabitlerin çeşitlenmesi formülü) ©(t ) ile (2.2.1) denkleminin ©(t 0 ) = I koşulunu
sağlayan temel matrisini gösterelim. Bu durumda t 0 2 (r 1 , r 2 ) olmak üzere (2.2.13) denkleminin
x(t 0 ) = x 0 başlangıç koşulunu sağlayan çözümü
x(t ) = ©(t )x 0 +
Zt
t0
©(t )©°1 (s)B (s) ds
(2.2.14)
eşitliği ile verilir.
İspat Sonuç 2.2.7 gereği (2.2.1) denkleminin y(t 0 ) = x 0 koşulunu sağlayan y(t ) çözümünün y(t ) =
©(t )x 0 olduğunu biliyoruz. Şimdi c vektörünün sabit olmayıp, t 2 (r 1 , r 2 ) için değişken bir c(t ) :=
(c 1 (t ), c 2 (t ), . . . , c n (t ))T , c(t 0 ) = x 0 vektörü olduğunu varsayıp x(t ) := ©(t )c(t ) fonksiyonunun (2.2.13)
denkleminin çözümü olması için (bu mümkün ise) c(t ) fonksiyonunun ne olması gerektiğini araştıralım. Varsayalım ki
x(t ) = ©(t )c(t ),
c(t 0 ) = x 0
(2.2.15)
fonksiyonu (2.2.13) denkleminin bir çözümü olusn. Bu durumda türev alarak
x 0 (t ) = ©0 (t )c(t ) + ©(t )c 0 (t )
eşitliğini, yani
A(t )x(t ) + B (t ) = A(t )©(t )c(t ) + ©(t )c 0 (t ) = A(t )x(t ) + B (t )c 0 (t )
Bölüm 2. Lı̇neer Sı̇stemler
44
eşitliğini elde ederiz. Bu eşitlikten de anlaşıldığı gibi B (t ) = ©(t )c 0 (t ) eşitliği sağlanır. Ayrıca © bir
temel matris olduğundan tersi vardır, dolyaısıyla
c 0 (t ) = ©°1 (t )B (t ),
eşitliği sağlanır. Buradan da
c(t ) = x 0 +
Zt
t0
c(t 0 ) = x 0
©°1 (s)B (s) ds
elde edilir ki böylece (2.2.15) gereği ispat tamamlanır.
Á
Uyarı 2.2.18 Temel matris ve bunun tersini içerdiğinden hesaplamalarda (2.2.14) formülü n > 3
için kullanışlı değildir. n = 3 durumunda bile temel matrisi hesaplamak çok zordur, yada imkansızdır. Fakat bu formül çözümlerin kalitatif özelliklerinin araştırılmasında çok önemli bir araçtır.
Bazı kullanım alanlarını ilerleyen bölümlerde göreceğiz. Œ
Uyarı 2.2.19 f (t , x) fonksiyonu r 1 < t < r 2 ve kxk < 1 bölgesinde sürekli olmak üzere
x 0 = A(t )x + f (t , x)
(2.2.16)
denklemi için de (2.2.14) benzeri bir formül benzer bir yöntemle elde edilebilir. Bu durumda ©(t )
ile (2.2.1) denkleminin ©(t 0 ) = I koşulunu sağlayan bir temel matrisi gösterilmek üzere, (2.2.16)
denkleminin x(t 0 ) = x 0 koşulunu sağlayan çözümü
x(t ) = ©(t )x 0 +
Zt
t0
©(t )©°1 (s) f (s, x(s)) ds
eşitliğini sağlar. Œ
A(t ) matrisinin sabit bir matris olması durumunda, yani
x 0 = Ax + B (t )
(2.2.17)
denklemi için (2.2.14) formülü daha da basitleşir. Sıradaki sonuçla bunu veriyoruz.
Teorem 2.2.20 ©(t ) matrisi x 0 = Ax denkleminin ©(0) = I koşulunu sağlayan bir temel matrisi
olsun. Bu durumda (2.2.17) denkleminin x(t 0 ) = x 0 koşulunu sağlayan çözümü
x(t ) = ©(t )x 0 +
Zt
t0
©(t ° s)B (s) ds,
t 2 (r 1 , r 2 )
ile verilir.
İspat Her Æ reel sayısı için ©(t )©°1 (Æ) = ©(t ° Æ) olduğunu göstereceğiz. ©(t ) matrisi x 0 = Ax
denklemini sağladığından ©1 (t ) := ©(t )©°1 (Æ) matrisi de aynı denklemi ve ©1 (Æ) = I başlangıç
koşulunu sağlar. Diğer yandan ©2 (t ) := ©(t ° Æ) fonksiyonu da
©02 (t ) = ©0 (t ° Æ) = A©(t ° Æ) = A©2 (t )
olup x 0 = Ax denklemini sağlar. Ayrıca başlangıç koşulu da ©2 (Æ) = ©(0) = I biçimndedir. Böylece
çözümün tekliği gereği ©1 (t ) ¥ ©2 (t ) olmalıdır.
Á
Yrd. Doç. Dr. Süleyman ÖĞREKÇİ