Çoklu-Anten Çok-Gönderim-Yollu Sönümlemeli

Çoklu-Anten Çok-Gönderim-Yollu Sönümlemeli CDMA Kanallarında Uzaysal
Alım Çeşitliliği ve Işın Oluşturmanın Kodlanmış Hata Oranı Tabanlı
Karşılaştırmalı Analizi
Özgür Ertuğ
Elektrik Elektronik Mühendisliği Bölümü
Gazi Üniversitesi, Ankara
e-posta: [email protected]
Özet
Çoklu-anten bir CDMA sisteminde antenlerin uzaysal
alım çeşitliliği veya ışın oluşturma arasında
paylaştırılması sistemin erişebileceği kapasite ve kalite
üzerinde önemli bir rol oynamaktadır. Bu bildiride alıcı
antenlerin uzaysal alım çeşitlilği ve ışın oluşturma
arasında bölümlendiği RAKE almaç ve MRC
birleştirim tabanlı bir alıcı yapısı önererek istatistiki
kodlama tabanlı hata eksponentlerine bağlı kodlanmış
hata oranlarını çok-gönderim-yollu Rayleigh yavaş
sönümlemeli kanallarda bularak alım çeşitliliği ve ışın
oluşturma arasındaki kazancı karşılastırmalı olarak
incelemekteyiz .Sonuçlarımız her çok gönderim yolu
sayısında belirli bir kodlanmış hata oranı tabanına
yakınsamasına rağmen çeşitlilik gruplarının sayısının
arttırılmasının antenlerin ışın oluşturmaya ayrılmasına
nazaran daha iyi güç verimliliği sağladığını ortaya
koymaktadır.
Anahtar Kelimeler: çoklu-anten CDMA, çeşitlilik alımı,
ışın oluşturma, istatistiki kodlama hata eksponentleri
Bölüm.3'te, kodlanmış hata oranlarını istatistiki-kodlama
tabanlı hata eksponentleri analizine bağlı olarak
bulmaktayız. Bölüm.4'teki nümerik sonuçlar ve
tartışmamız Bölüm.5'teki sonuçlar kısmı tarafindan takip
edilmektedir.
2. SİSTEM MODELİ
Ele aldığımız çip/sembol senkron yukarı-hat zamanla
değişken çok-gönderim-yollu Rayleigh speküler yavaş
sönümlemeli çoklu-anten CDMA sisteminin modeli
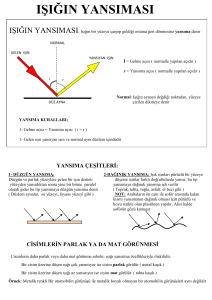
Şekil.1'de verilmiştir. Sistemde K adet eşit-güç kullanıcı
olup yayma faktörü L idir. Kullanıcıların sembolleri sembol
SNR'i SNRs güç-limitli istatistiki kompleks Gaussian
kodlarla kodlanmıştır ve yayma işleminin ise yayma
dizinleri üzerinden ortalama sonuçlara ulaşma amacıyla
normu normalize edilmiş eşit-olasılıklı ikili antipodal
çiplerden olusan vektörlerle yapıldığı farzedilmiştir [2].
1. GİRİŞ
Çoklu-anten kablosuz alıcı sistemlerinde uzaysal
haberleşme boyutunu belirleyen anten sayısının alım
çeşitliliği ve ışın oluşturma arasında bölümlenmesinin
sistemin erişebileceği kapasite ve kalite uzerinde büyük
etkisi vardir. Bu etki ilk olarak Nezafat ve Kaveh [1]
tarafindan frekans-düzgün Rayleigh sönümlemeli bir
çoklu-anten alım sisteminde antenlerin ışın-oluşturma
gruplarına bölünerek bu bölümler üzerinden uzaysal alım
çeşitliliği yapılması altında ergodik ve yetmezlik
kapasitelerinin incelenmesiyle yapılmıştır.
Böyle bir etkinin analizi özellikle bir çoklu-erişim
CDMA sisteminde ve çok-gönderim-yollu sönümlemeli
kanallarda daha da önem arzetmektedir. Biz bu bildiride
uzaysal alım çeşitliliği ve ışın oluşturma arasindaki anten
bölümlenmesinin kodlanmış hata oranlarına etkisini çokgönderim-yollu sönümlemeli CDMA kanallarında
inceleyeceğiz. Bölüm.2'de sistem modelini vermekteyiz.
Şekil 1. Göndericiler ve hibdrid almaç yapısı
Her kullanıcının tek gönderici anteni olup almaçtaki
anten sayisi M idir. Almaçtaki bu antenler Md adet
çeşitlilik grubuna bölünmüş olup her grupta Mb adet ışın
oluşturma anteni bulunmaktadır. Her çeşitlilik grubunda
ışın oluşturma antenleri arası uzaklık
dm ≤
λc
2
olup
MKD ×1
(1)
ki burada D her kullanıcının gönderim yolu sayısı, R MKD
A
MKD × M KD
d
x MKD çapraz korelasyon matrisi,
∈C
blok-diyagonal dizin yönlendirme vektörleri matrisi,
H∈C
Pe , K ≤ exp( − NE ( Rsum ))
w ∈C
MKD ×1
{ww } R
ise kovaryans matrisi E
= olan
sıfır-ortalama sirküler-simetrik kompleks-Gaussian ardalan
gürültüsü vektörüdür.
H
3. KODLANMIŞ HATA ORANI
Bu bölümde çoklu-anten kullanımında uzaysal alım
çeşitliliği ve ışın oluşturma arasındaki kazanç farklılığını
belirlemek icin toplam-oranlar istatistiki kodlama istatistiki
kodlama hata eksponentlerine bağlı olarak ML belirleme
için rastgele kod kitapçıkları üzerinden averajlanmış üstsınır sembol hata oranlarını türetmekteyiz. Hata
eksponentleri istatistiki-kodlama için ML belirleme ile elde
edilebilecek rastgele kod kitapçıkları üzerinden
averajlanmıs sembol üst-sınır eksponaniyel hata
oranlarının üzerinde bit/sembol cinsinden orana bağlı bir
eksponent olup sıfıra gittikleri nokta enformasyon-teoretik
kapasiteyi göstermektedir [3].
İstatistiki ikili antipodal normalize yayma dizinlerinden
dolayı çapraz korelasyon matrisi R simetrik olup diyagonal
elemanları 1 ve non-diyagonal elemanları merkezi-limit-
1
teoreminden dolayı sıfır-ortalama
-varyans Gaussian
L
rastsal değişkenlerdir [4].
Varanasi ve Guess’in [5] Gaussian çoklu-erişim kanalı
için türettiği istatistiki-kodlama hata eksponenti sonucunu
enterferans-limitli durumda incelediğimiz vektör Gaussian
(3)
ρ ∈[ 0 ,1]
E0 , K ( ρ ) =
ρ

K
1
∑ log1 + 1 + ρ SIR
2
( SGA )
k

k =1
ki burada maksimize edici parametre
( SGA)
k
SIR
herhangi
bir
eşit-güç



(4)
ρ =1
olup
kuıllanıcının
enterferansının averaj güç değerinin kullanımıyla elde
edilen standard Gaussian yaklaşımı sinyal-enterferans oranı
rastsal değişkenidir. Ayrıca üst-sınır sembol hata oranının
dış-bükeyliğinden dolayı Jensen eşitsizliği ile diğer bir üstsınır sembol hata oranı da şu şekilde verilebilir:

K

Pe, K ≤ exp − N  log 1 + E SIRk( SGA) − ρRsum   (5)
2


(
{
})
ve E{.} istatistiki averaj operatörüdür.
Hibrid almaç incelendiğinde her eşit-güç kullanıcı için
standard Gaussian yaklaşımı altında sinyal enterferans
oranının şu şekilde verildiği görülür:
M d KD × K
blok-diyagonal sıfır ortalama 1-varyans
kompleks Gaussian kanal katsayılarından oluşan kullanıcı
kanal dürtü tepkisi vektörlerinin matrisidir. Vektör
(2)
E ( Rsum ) = max {E0, K ( ρ ) − ρRsum }
λc
taşıyıcı frekansı idir. Çeşitlilik grupları arası uzaklık ise
bağımsız sönümleme kanalları elde edilmesi amacı ile
taşıyıcı frekansın 10 katından büyük seçilmiştir. Hibrid
almaçta çip ve kod uyumlu filtrelerden oluşan RAKE
katından sonra her kullanıcının her gönderim yolu için
konvansiyonel ışın oluşturma işlemi gerçekleştirilmektedir.
Bu elde edilen istatistikler ise her kullanıcının kanalının
almaçta komple olarak bilinmesinin farzedilmesi ile
maksimal-oranlar birleştiriminden (MRC) geçirilmekte ve
kullanıcı sembolleri ML (maximum-likelihood) belirleme
ile bulunmaktadır.
Çip ve kod uyumlu filtreleri takiben elde edilen kesiklizaman vektörel sinyal şu şekildedir:
y = RHAs + w, y ∈ C
çoklu-erişim sistemi için ilerletirsek üst-sınır sembol hata
oranı için şu sonuca varırız:
hkH R kkH Φ kk R kk hk
SIRk( SGA) =
K
∑h
ki burada R ve R
k '=1, k '≠ k
kk
H
k'
kk '
rastsal matrisleridir.
(6)
2
çapraz korelasyon matrisin kk.
MdD×MdD
ve kk’.
{ }
R Φ kk 'R kk 'hk ' + E nk
H
kk '
diyagonal ve off-diyagonal
Φij = A iH A j
matrisleri ise ışın
oluşturma güç kaybı rastsal değişkenlerinin rastsal
matrisleri
olup
bu
rastsal
değişkenler
Φ (θ ,θ
ij
n
m
) = aiH (θ n )a j (θ m )
tanımlanmaktadır.
[−π , π ]
Ertuğ
2
[6]’da
olarak
bu
değişkenlerin
arasında dağılımlı D.O.A’lar için averaj değerinin ışın
oluşturma antenlerinin sayısı M b ve uzaysal örnekleme
oranı
ρ=
dm
λc
için şu şekilde verildiğini göstermiştir:
{
S ( M b , ρ ) = E w H (θ i )a(θ j )
=
Simetrik
1
2M b2
2
}
3M b − 2
∑ CM b (m).J 02 (2πρ (m − M b ))
(7)
m =1
katsayılar
şu
şekilde
verilmekte
olup:
CM ( m) = {1, 2,..., M − 1, M + 1, M + 1,..., M + 1, M − 1,
M − 2,...,2,1} dizin ortasındaki M+1 katsayılarının
sayısı M idir.
Arkaplan gürültüsü istatistiğinin açılımı ise :
nk = hkH A kH w k w kH A k hk
2
(8)
Çapraz korelasyon matrisinin diyagonal submatrislerinin
özdeğer dağılımı deterministik 1 olup off-diyagonal
submatrislerin özdeğer dağılımı ise averaj diyagonal
toplamı (trace) tanımından dolayı

1 
 idir.
N  0,
 M d DL 
Bu bilgilere bağlı olarak rastsal matris çarpımı grupları
üzerinden averajlama kurallarını [2] kullanarak standard
Gaussian yaklaşımı altında sinyal-enterferans oranının
averaj değerini şu şekilde elde edebiliriz:
{
}
E SIRk( SGA) =
M d DSNRs
K
S ( M b , ρ )SNRs + M d D
M d DL
(9)
ve üst-sınır sembol hata oranı da bu değer üzerinden (5) ile
verilmektedir.
4. NÜMERİK SONUÇLAR VE
TARTIŞMA
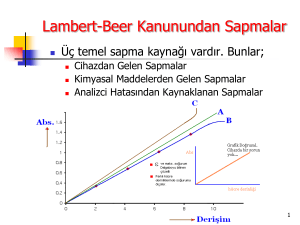
(5) ve (9) ile verilen üst sınır sembol hata oranı Şekil 2.’de
128 anten için Md’ye karşılık D=1,2,3,4 için verilen
değerlerde çizilmiştir.
Şekil 2. Toplam 128 anten için
M d ’ye karşılık
log( Pe ) ; K=20, L=7, N=4, D=1:4, ρ = 0.5 ,
SNRs = 5 dB, Rsum = 16 bit/sembol
Görülebileceği gibi sabit anten sayısı için çeşitlilik
gruplarının sayısı artırılırken kodlanmış hata oranı
düşmektedir. Yine de tüm D değerleri için grafikler
çeşitlilik gruplarının sayısı artarken belirli bir tabana
yakınsamaktadır. Ayrıca birleştirimde kullandığımız D ile
belirlenen ne kadar çok gönderim yolu kanalımız var ise
güç verimliliğimiz o kadar artmaktadır ki bu da antenlerin
bölümlenmesine ek bir etki olarak ortaya çıkmaktadır. Çok
gönderim yolu sayısının artması durumunda da hata oranı
tabanı yeniden ortaya çıkmaktadır.
5. SONUÇLAR
Çoklu-anten CDMA sisteminde antenlerin uzaysal alım
çeşitliliği veya ışın oluşturma arasında bölümlenmesinin
sistemin erişebileceği hata oranı üzerinde büyük etkisi
vardır. Bu makalede alıcı antenlerin uzaysal alım çeşitlilği
ve ışın oluşturma arasında bölümlendiği bir alıcı yapısı
önererek istatistiki-kodlama tabanlı hata eksponentlerine
bağlı kodlanmış hata oranlarını bularak alım çeşitliliği ve
ışın oluşturma arasındaki kazancı karşılastırmalı olarak
inceledik. Türettiğimiz üst sınır sembol hata oranı
formülüne göre her çok gönderim yolu sayısında belirli bir
kodlanmış hata oranı tabanına yakınsamasına rağmen
çeşitlilik gruplarının sayısının arttırılmasının antenlerin
ışın oluşturmaya ayrılmasına nazaran daha iyi güç
verimliliği sağladığını ortaya koymaktadır.
6. KAYNAKÇA
[1] M. Nezafat ve M. Kaveh. Analysis of diversity,
beamforming and hybrid diversity-beamforming
systems. Proceedings of 2003 IEEE International
Conference on Acoustics, Speech and Signal
Processing, Nisan 2003, pp. 369-372.
[2] S. Verdu. A. M. Tulino. Random Matrix Theory for
Wireless Communications. Now Publishers, 2004.
[3] R. G. Gallager. Information Theory and Reliable
Communications. John Wiley&Sons Inc., 1968.
[4] S. Yoon and Y. Bar-ness. Performance analysis of
linear multiuser detectors for randomly-spread cdma
using gaussian approximation. IEEE Journal on
Selected Areas in Communications, vol. 20, no. 2, pp.
409-418, Şubat 2002.
[5] T. Guess and M. K. Varanasi. Error-exponents for
maximum-likelihood and successive decoders for the
Gaussian CDMA channel. IEEE Transactions on
Information Theory, vol. 46, no. 4, pp. 1683-1691,
Temmuz 2000.
[6] Özgür Ertuğ. Lineer çoklu-anten dizinlerinin
düzgün dağıulımlı rastgele dalga gelim yönlerine bağlı
averaj maksimum-SIR uzaysal filtreleme bastırımı.
2006 3. Ulusal URSI Konferansı, pp. 465-467, 6-8
Eylül, Ankara, Türkiye.