Benzer Terim: Bir cebirsel ifadede değişkeni ve değişkenin kuvveti

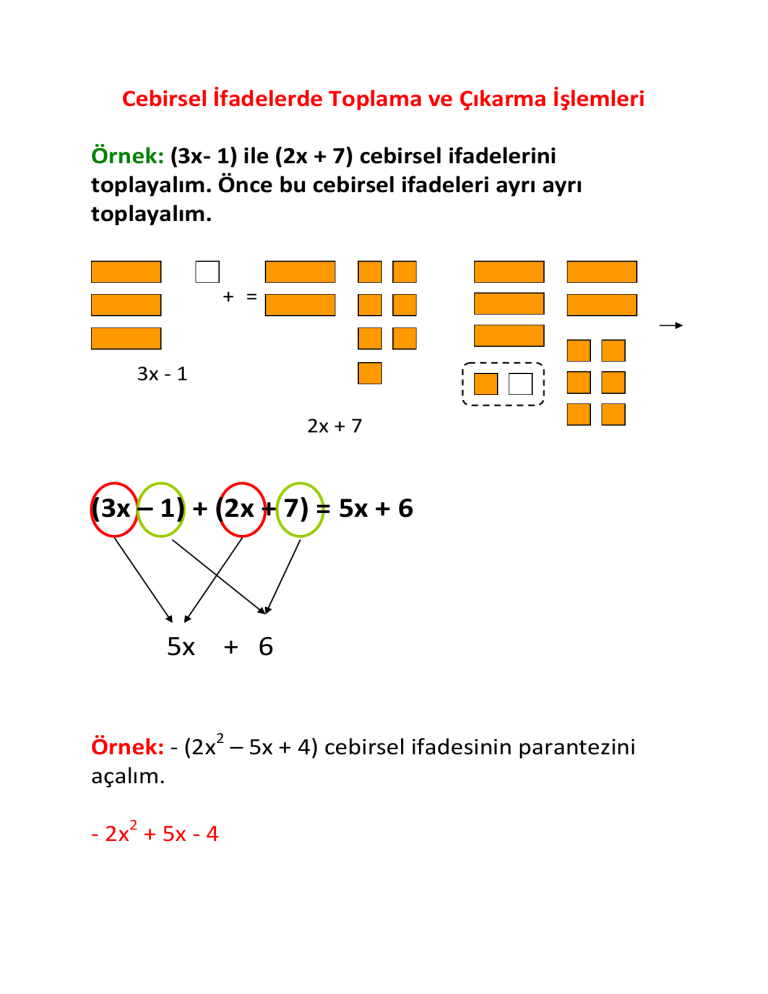
Cebirsel İfadelerde Toplama ve Çıkarma İşlemleri
Örnek: (3x- 1) ile (2x + 7) cebirsel ifadelerini
toplayalım. Önce bu cebirsel ifadeleri ayrı ayrı
toplayalım.
+ =
3x - 1
2x + 7
(3x – 1) + (2x + 7) = 5x + 6
5x + 6
Örnek: - (2x2 – 5x + 4) cebirsel ifadesinin parantezini
açalım.
- 2x2 + 5x - 4
Örnek: Aşağıda modellenen toplamalara ait cebirsel
ifadeleri yazınız.
+
+
=
=
+
=
Örnek: Aşağıdaki cebirsel ifadeler arasındaki toplama
ve çıkarma işlemlerini model kullanmadan yapalım.
a) (6x + 4) + (2x+1) = 8x + 5
b) (2x2 – 1) – (3x2- 5) = - x2+5
c)
(4x+5y) + (8x + y)=12x + 6y
d) (-5x+ 5y+18y) – 14y = -5x + 9y
e) (2a- 3b) – (4a- 5b) = -2a + 2b
f)
(2x + 1)+ (x+7) = 3x + 8
g)
(x+7) + (2x- 7) = 3x
h) (-3x+8) + (2x- 4) = - x + 4
i)
(-2x – 1)+(-x- 3) = - 3x – 4
Örnek: x=3 için aşağıdaki cebirsel ifadelerin değerlerini
bulunuz.
15 – 2x = 15 – 6 = 9
- 2x + x3 = -6 + (-27) = -33
- 9 + 2x – (2x)2 = -9 + 6 – 36 = -39
2.(x2 -1) + 5x = 2.(8) + 15 = 31
Cebirsel İfadelerde Çarpma İşlemi
1. model
a
b
2.(4a + 3b)
2. model
8a+6b
Örnek: Aşağıda verilen cebirsel ifadelerin çarpımlarının
en sade hallerini yazınız.
2a.3a= 6a2
-4.(2 - x)=-8+4x
-5a.(8a)=-40a2
x.(x+1)=x2+x
2.(x+3) = 2x + 6
2x.(2-3x)=4x-6x2
(x+1).(x+2)
(a - 1).(a + 3)
(x+5).(2x+8)
- 8.(2x+x- 10)
(2x- 1).(2x+3)
(-3x) + 2x.(x+1)
(a+5)2 = (a+5).(a+5)
(a-2)2 = (a-2).(a-2)
5y.(y- 4) + 6
x.(x- 2)+2x2
Cebirsel İfadelerle Çarpma İşleminin
Modellenmesi
x
2
-x
2
x -x 1 -1