Bir-fazlı Gerçek Transformatorlar

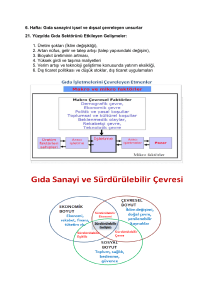
Bir-fazlı Gerçek Transformatorlar
1
Gerçek Transformatorlar
v1(t )  v1a (t )  R1i1(t )
v1a (t )
olur.
d1
 N1
dt
m
R1

v1(t)
L1
v1a (t )
i2(t)
i1(t)
e1(t)
l1
l2
e2(t)
L2
R2
v2 a (t )
yük
2
Gerçek Transformator
1 akısı primer sargısını keser. Eğer nüvenin geçirgenliği sonsuz kabul edilir ise,
relüktans (manyetik direnç) sıfırdır ve böylece sadece demir
nüve yolundan
devresini tamamlar. İdeal durumdan farklı olarak 1 'in çok küçük bir oranı hava
aralığından devresini tamamlar (kaçak l1), sekonder sargısını kesmez ve L1 kaçak
endüktansı veya X1 kaçak reaktansı ile temsil edilir. Geri kalan akı m hem primer
hem sekonder sargılarını kesen demir nüvedeki ortak akıdır. Bu durumda akı
denklemimiz aşağıdaki gibi tanımlanır.
1  l1  m
Bir önceki slaytta primer tarafı için gerilim denklemi; v1( t )
v1a (t )
v1(t )
d1
 N1
dt
dl1
dm
 R1i1(t )  N1
 N1
dt
dt
 v1a (t )  R1i1(t )
şeklinde yazılabilir.
3
Gerçek Transformator
dir ve bu değer faraday yazasına göre;
d l1
di1
L1
 N1
dt
dt
eşittir.
Aynı zamanda primer sargıda endüklenen gerilim;
d m
e1  N1
dt
olduğundan primer tarafı için son olarak elde edilen gerilim
denklemi aşağıdaki gibi tanımlanır.
v1(t )  R1i1(t )
di1
 L1
 e1(t )
dt
Gerçek Transformator-Manyetik yapı
1
+
F1=N1 i1
m
l1
Rl1
2
Rm
l2
Rl2
+
F2=N2 i2
5
Gerçek Transformator-Manyetik yapı
1
m
Rm
l1
+
2
l2
Rl2
Rl1
F1=N1 i1
m
F1=N1 i1
+
F2=N2 i2
 m Rm  N1i1  N 2 i2
Rm
+
Şekildeki manyetik eşdeğer
devreye bakılırsa, F1 ve F2
arasındaki fark sonucu
manyetik
devrede
m
akısının üretildiği açıkça
görülür.
Matematiksel
olarak bu durum aşağıdaki
gibi tanımlanır.
+
F2=N2 i2
Prof. Dr. Güngör Bal, [email protected]
Gazi Üniversitesi
6
Gerçek Transformator - Uyartım devresi
m Rm  N1i1  N 2i2
F1 ve F2 arasındaki fark sonucu manyetik devrede m akısının üretildiğini
söyleyen bu denklemi yeni bir akım tanımlamasıyla aşağıdaki gibi yazılabilir.
m Rm  i N1
N1i  N1i1  N 2 i2
N2
i1  i 
i2
N1
ve değer aynı zamanda; i1
 i  i2'
şeklinde yazılabilir.
Bu sonuç bize şunu söyler;
Primer akımı, uyartım akımı ile primere aktarılmış sekonder akımının toplamı olarak
ifade edilebilir.
7
Gerçek Transformator - Uyartım akımı
𝑖∅ uyartım akımı şekildeki fazör diyagramında gösterildiği gibi 𝑖𝑚 ve 𝑖𝑐 şeklinde iki
bileşeni bulunmaktadır. 𝑖𝑚 bileşeni mıknatıslanma akımı olarak adlandırılır ve
manyetik akı ∅ ile aynı fazda olduğu kabul edilmektedir. 𝑖𝑐 bileşeni ise nüve
kayıplarını temsil eder ve 𝐸1 ile fazda olduğu kabul edilmektedir.
Bu durumda uyartım akımının varlığı transformatörün gerçek eşdeğer devresinde
göstermek için bir direnç kondüktansı (Elektriksel Direncin Tersi) 𝐺𝑐 ile bir sargı
süseptansı (süseptans, elektronik devrelerde iletkenlik katsayısının imajinel kısmıdır)
𝐵𝑚 ’ nin paralel kombinasyonu kullanılarak temsil edilir.
Ic
qc
Im

E1
I
Uyartım akımının fazör diyagramı
Gerçek Transformator - Eşdeğer devre
Transformatörün gerçek devresi elde edebilmek için son olarak sekonder tarafla
ilgilenilir. Sekonder sargıdan geçen 𝑖2 akımının ürettiği manyetik akının düşük bir
oranı devresini havadan tamamlarken büyük bir oranı ise nüveden devresini
tamamlar. Primer sargı için kullanılan kurallara benzer olarak da sekonder sargının
kaçak endüktansı 𝐿2 veya reaktansı 𝑋2 ve sargı direnci 𝑅2 tanımlanarak bir
transförmatörün gerçek devresi aşağıdaki gibi elde edilir.
Bir transformatorun elektrik devresi
Gerçek Transformator - Eşdeğer devre
Elde edilen bu eşdeğer devrenin sekonder tarafı primer tarafına aktarılmasıyla
aşağıdaki şekilde görülen tranförmatörün T eşdeğer devresi elde edilir.
2
N 
R2'   1  R2
 N2 
2
N 
X 2'   1  X 2
 N2 
I 2' 
N2
I2
N1
V2' 
N1
V2
N2
Gerçek Transformator - Eşdeğer devre
Örnek: (Elektrik Makinaları-1, Prof. Dr. Güngör BAL, sayfa 116)
Lütfen Not Alınız.
Gerçek Transformator – Yaklaşık eşdeğer devreler
I1
I2
Yaklaşık eşdeğer devreler; şekildeki T eşdeğer devre pratikte ve özellikle de
+
+
I
+
+
jX
jX
R
R
güç sistemleri
uygulamalarında gerekenden çok daha
hassas sonuçlar verir. T
eşdeğer
devre basit olmasına rağmen
bu
devrenin yaklaşık eşdeğer devreleri
V
E
E
V
G
B
kullanılabilir. Nüveyi temsil eden paralel kolun empedansı primer ve sekonder
sargıların
empedansından çok büyüktür
ve
dolayısıyla paralel- kolun akımı yani
uyartım akımı ( 𝐼∅ ) çok küçüktür.
İşte bu nedenden dolayı primer sargı
ideal tramsformator
N
empedansına (𝑅1 + 𝑗𝑋1 ) düşen Ngerilim
ihmal
edilecek kadar az olmasından
(a)
I’
dolayı paralel kol şekilde gösterildiği gibi ya primer Itarafa yada sekonder tarafa
I
I’
+
I
kaydırılabilir.
+
R
jX

1
1
1
c
2
2
1
m
2
2
2
1
2
1
1
+
2
I
jX1
R1
+
Im
Ic
R’2
V1
eq
eq
Im
+
Ic
JX’2

Gc
V’2
Bm
V’2
V1
Gc
Bm
I’2
I1
I
Ic
V1
-
Gc
-
-
-
-
+
E1
Req
jXeq
-
+
Req
I
jXeq
Ic
Im
Bm
I’2
I1
(b)
+
(a)
V’2
-
V1
+
Gc
+
Im
Bm
V’2
-
(b)
Gerçek Transformator – Yaklaşık eşdeğer devreler
-
-
(a)
I’2
I1
I
+
+
jXeq
+
Req
Gc
I
jXeq
Im
Ic
V1
Req
I’2
I1
Ic
V’2
Bm
-
-
+
V1
Gc
+
Im
Bm
V’2
-
-
(a)
(b)
I
I’
Bu yaklaşık
devrelerde artık primer
ve sekonder empedansları seri bağlı durumu
I1=I’2
I
+empedans (𝑅
+gelmiştir ve
R bu durum
jX
bir eşdeğer
+𝑗𝑋
)
ile
temsil
edilebilir. Yani;
𝑒𝑞
𝑒𝑞
1
2
eq

eq
Ic
+
V1
Gc
Im
Bm
V’2
+
Req
+
jXeq
𝑅𝑒𝑞 = 𝑅1 + 𝑅2′
V
′
- 𝑋
=
𝑋
𝑒𝑞
1 + 𝑋2
V’2
1
(b)
-
(c)
I1=I’2
+
V1
Req
jXeq
I1=I’2
+
V’2
+
jXeq
+
I
+
Gerçek Transformator – Yaklaşık eşdeğer devreler
+
Req
jXeq
+
Req
jXeq
+
V1
+
Ic
I Im
I
Gcc
ImB
+
V’2
m
V’2
B
G
Daha ileri bir yaklaşık devre ise şekilde gösterildiği
gibi paralel kol kaldırılarak
gerçekleştirilebilir. Böylece
eşdeğer devre çok daha basit
hale getirilebilir. Devreyi
(b)
daha da basitleştirmek istediğimizde eşdeğer
direnç ihmal edilerek devrede sanki de
(b)
tek bir eşdeğer endüktans varmış gibi düşünülebilir.
V1
c
m
I1=I’2
I1=I’2
+
+
Req
Req
+
+
jXeq
jXeq
V1
V1
V’2
V’2
-
-
(c)
(c)
I1=I’2
I1=I’2
+
+
jXeq
jXeq
+
+
V’2
V’2
V1
V1
-
-
-
(d)
(d)
Gerçek Transformator - Eşdeğer devre
Örnek: (Elektrik Makinaları-1, Prof. Dr. Güngör BAL, sayfa 120)
Çok çok faydalı bir soru lütfen not alınız.
Transformatorların Performans Ölçütleri
Belirli bir uygulama için uygun transformatorun seçimi önemli
performans ölçütlerinin değerlendirilmesini gerektirir.
Önemli performans ölçütleri:
• Gerilim regülasyonu
• Verim
Prof. Dr. Güngör Bal, [email protected]
Gazi Üniversitesi
Performans Ölçütleri - Gerilim regülasyonu
• Gerilim regülasyonu
Sabit bir güçkatsayısında yükün sıfırdan anma değerine kadar
değişmesi sonucu sekonder gerilimindeki değişimdir.
V2  yüksüz  V2 anma
%VR 
100
V2 anma
Performans Ölçütleri - Gerilim regülasyonu
IL2
+
Req2
+
jXeq2
V1/a
-
Sekondere göre yaklaşık eşdeğer devre
ZL2
-
V2
(V1 / a)  V2
%VR 
100
V2
Performans Ölçütleri - Verim
Verim:
Transformatorun çıkış gücünün giriş gücüne oranıdır.
P2

P1
 
P2  V2 I L cos  L
Pl  Pc  I L2 Req
P1  P2  Pl

V2 I L cos L
 
V2 I L cos L  Pc  I L2 Req
Transformatorların güçleri arttıkça verimlerinin de artığı
genellemesi yapılabilir. Bir transformatorun verimi yük akımı ile
değişir.
Prof. Dr. Güngör Bal, [email protected]
Gazi Üniversitesi
Performans Ölçütleri - Maksimum Verim
Maksimum verim şartı:

0
I L
P2

P1
P2
( )
P1
0
I L
 P2
P1 
I L



I L
 P2
P1 
 I L

 P1
  P2 

 I L
P12

 P1
  P2 

 I L
P12


 0


 0
P1 P1 / I L

P2 P2 / I L
P1

P2
Prof. Dr. Güngör Bal, [email protected]
(V2 I L cos L  Pc  I L2 Req ) / I L
(V2 I L cos L ) / I L
Gazi Üniversitesi
Performans Ölçütleri - Maksimum Verim
Pc  2 I L2 Req   I L2 Req 
P1 V2 cos L  2 I L Req

P2
V2 cos L
Böylece maksimum verim şartı:
P1  P2  2 I L Req I L
P1  P2  2 I L2 Req
P1  P2  Pl
Pl  Pc 
2
IL
Pc  I L2 Req 
Maksimum verim şartı; nüve kayıpları
ile sargıların direnç kayıpları eşit
olduğunda sağlanmaktadır.
Req 
2 I L2 Req   Pc  I L2 Req 
Prof. Dr. Güngör Bal, [email protected]
Gazi Üniversitesi
 max
100
% verim

340W
Pcu
90
Pc
120W
0
50
100
% anma ak ım ı
150
Yük akımı ile verim, bakır kayıpları ve nüve kayıplarının değişimi
Prof. Dr. Güngör Bal, [email protected]
Gazi Üniversitesi
G ü ç k a yıpları
Performans Ölçütleri - Verim