Kuvvet çifti vektörleri

Seventh Edition
VECTOR MECHANICS FOR
ENGINEERS: STATICS
Ferdinand P. Beer
E. Russell Johnston, Jr.
Ders Notu:
Hayri ACAR
İstanbul Teknik Üniveristesi
3. Rijit Cisimler:
Eşdeğer Kuvvet
Sistemleri
Tel: 285 31 46 / 116
E-mail: [email protected]
Web: http://atlas.cc.itu.edu.tr/~acarh
© 2002 The McGraw-Hill Companies, Inc. All rights reserved.
• Bir cisimi maddesel nokta olarak kabul etmek her zaman uygun değildir.
Genelde, cisimin boyutları ve kuvvetlerin uygulama noktası önemlidir.
• Mekanikte bir çok cisim rijit olarak kabul edilebilir: kuvvet etkisi altında
şekil değişimi çok küçüktür ve denge koşullarını ve cisimin hareketinin
etkilemez.
• Bu bölümde, rijit cisime uygulanan kuvvetlerin etkisi ve verilen kuvvet
sisteminin daha basit olan eşdeğer kuvvet sistemine dönüştürülmesi
incelenecektir
• kuvvetin bir noktaya göre momenti
• kuvvetin bir eksene göre momenti
• kuvvet çiftinin momenti
• Bir rijit cisime etki eden herhangi bir kuvvet sistemi, bir noktaya etki
eden bir kuvvet ve kuvvet çiftinden oluşan eşdeğer bir sisteme
dönüştürülebilir.
Dış ve İç Kuvvetler
• Rijit cisimlere etki eden
kuvvetler iki gruba ayrılır:
- Dış kuvvetler
- İç kuvvetler
• Dış kuvvetler serbest cisim
diyagramında gösterilir
• Her kuvvet cisime öteleme
hareketi, dönme hareketi veya
her ikisini birlikte yaptırabilir.
Kaydırılabilme İlkesi: Eşdeğer Kuvvetler
• Bir kuvvetin tesir çizgisi boyunca
kaydırıldığında, cisimin denge veya
hareket şartlarında değişiklik olmaz.
• F kuvvetinin uygulama noktasını
ön tampondan arka tampona
kaydırılması kamyonun hareketini
değiştirmez.
• Kaydırılabilme ilkesi iç kuvvetler
için ve şekil değiştiren cisimler
için kullanılamaz.
İki Vektörün Vektörel Çarpımı
• Bir kuvvetin bir noktaya göre momenti, vektörel
çarpım uygulamaları ile daha iyi anlaşılabilir.
• P ve Q vektörlerinin vektörel çarpımı şu şekilde
tanımlanır:
1. Sonuç vektörü V, P ve Q vektörlerinin
oluşturduğu düzleme diktir.
2. V vektörünün şiddeti:
V = P Q sin θ
3. V vektörünün yönü sağ el kuralı ile belirlenir.
• Vektörel çarpım özellikleri:
Q × P = −( P × Q )
P × (Q1 + Q2 ) = P × Q1 + P × Q2
( P × Q ) × S ≠ P × (Q × S )
Sağ el kuralı
Vektörel Çarpım: Dik Bileşenler
• Kartezyen birim vektörlerin vektörel çarpımı:
r r
i ×i = 0
r r r
i× j =k
r r
r
i ×k = − j
r r r r
r r
j × i = −k k × i = j
r r
r r
r
j× j =0
k × j = −i
r r
v r r
j ×k = i
k ×k = 0
• P ve Q vektörlerinin vektörel çarpımı:
r
r
r
r
r
r
r
V = Px i + Py j + Pz k × Q x i + Q y j + Q z k
r
r
= Py Q z − Pz Q y i + ( Pz Q x − Px Q z ) j
r
+ Px Q y − Py Q x k
(
(
)
(
r
i
= Px
Qx
r
j
Py
Qy
r
k
Pz
Qz
) (
)
)
Bir Kuvvetin Bir Noktaya Göre Momenti
• Bir kuvvet vektörü şiddeti ve yönü ile tanımlanır.
Bu kuvvetin cisim üzerindeki etkisi uygulama
noktasına bağlıdır.
• F kuvvetinin O noktasına göre momenti:
MO = r × F
• Moment vektörü MO O noktası ve F kuvvetinin
oluşturduğu düzleme diktir.
• MO momentinin şiddeti cisimin kuvvet etkisi altında
dönme eğiliminin ölçüsüdür. Yönü sağ el kuralı ile
belirlenir.
M O = rF sin θ = Fd
• Aynı şiddetli ve yönlü moment oluşturan her hangi bir
kuvvet F’ , F kuvvetinin eşdeğeridir.
yer vektörü
• İki-boyutlu yapılarda uzunluk ve genişlik vardır. Derinlik
ihmal edilir. Kuvvetler bir düzlem içindedir.
• Yapı düzlemini O noktası ve F kuvveti oluşturur.
MO: kuvvetin O noktasına göre momentidir ve düzleme
diktir.
• Kuvvet, yapıyı saat ibrelerinin ters yönünde çevirmeye
çalışırsa moment yönü düzlemden dışarıya doğrudur.
Bu yön pozitif yön olarak seçilir.
• Kuvvet, yapıyı saat ibrelerinin yönünde çevirmeye
çalışırsa moment yönü düzlemden içeriye doğrudur.
Bu yön negatif yön olarak seçilir.
Varignon Teoremi
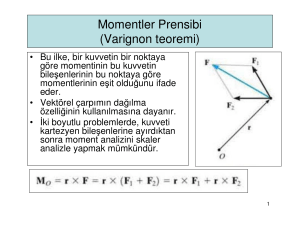
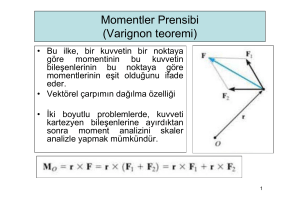
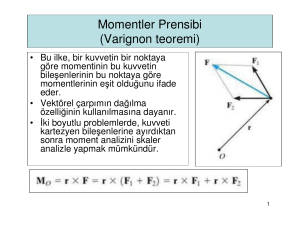
• Bir noktaya etkiyen bir çok kuvvetin
bileşkesinin bir O noktasına göre momenti,
bu kuvvetlerin O noktasına göre
momentlerinin toplamına eşittir:
r r r
r r r r
r × (F1 + F2 + L) = r × F1 + r × F2 + L
Momentin Dik Bileşenleri
F kuvvetinin O noktasına göre momenti:
r
r r
r
r = xi + yj + zk
r
r
r
r
F = Fx i + Fy j + Fz k
r
r r
MO = r × F,
r
MO = x
r
j
r
k
y
z
Fx
Fy
Fz
r
i
r
r
r
= ( yFz − zFy )i + ( zFx − xFz ) j + (xFy − yFx )k
r
r
r
r
M O = M xi + M y j + M z k
F kuvvetinin B noktasına göre momenti:
r
r
r
M B = rA / B × F
r
r r
rA / B = rA − rB
r
r
r
= (x A − xB )i + ( y A − y B ) j + (z A − z B ) k
r
r
r
r
F = Fx i + Fy j + Fz k
r
i
r
M B = (x A − xB )
Fx
r
j
( y A − yB )
Fy
r
k
(z A − z B )
Fz
İki-boyutlu yapılar için:
r
r
M O = (xFy − yFx )k
MO = MZ
= xFy − yFx
r
r
M O = ( x A − xB )Fy − ( y A − yB )Fx k
[
MO = MZ
= ( x A − xB )Fy − ( y A − yB )Fx
]
Örnek Problem 3.1
100 N’luk dik kuvvet O noktasından bağlanmış
şafta A noktasından etkimektedir.
a) O noktasına göre momenti,
24 cm
N
b) aynı momenti oluşturacak, A noktasına
uygulanacak yatay kuvveti,
c) aynı momenti oluşturacak, A noktasına
uygulanacak en küçük şiddetli kuvveti ,
d) aynı momenti oluşturacak 240 N’luk düşey
kuvvetin yerini,
e) b, c, ve d şıkkında elde ettiğiniz kuvvetlerin
orjinal kuvvete eşdeğer olup olmadığını,
belirleyiniz.
24 cm
N
a) Kuvvetin O noktasına göre oluşturduğu momentin
şiddeti, kuvvetin tesir çizgisiyle moment alma
noktası arasındaki dik mesafeyle çarpımı ile bulunur.
Moment saat ibreleri yönünde olduğuna göre, yönü
sayfa düzleminin içine doğrudur.
M O = Fd
d = (24 cm )cos 60° = 12 cm.
M O = (100 N )(12 cm )
M O = 1200 N ⋅ cm
b) Aynı momenti oluşturan A noktasına
uygulanacak yatay kuvvet:
24 cm
d = (24 cm )sin 60° = 20.8 cm
M O = Fd
1200 N ⋅ cm. = F (20.8 cm.)
1200 N ⋅ cm.
F=
20.8 cm
F = 57.7 N
24 cm
c) Aynı momenti oluşturan A noktasına uygulanacak
en küçük kuvvet:
Bunun için tesir çizgisi ile moment alma noktası
arasındaki dik mesafenin en büyük değere sahip
olması gerekir. F kuvvetinin şaft eksenine dik
olduğu durumda gerçekleşir.
M O = Fd
1200 N ⋅ cm = F (24 cm )
1200 N ⋅ cm
F=
24 cm
F = 50 N
d) aynı momenti oluşturacak 240 N’luk dik kuvvetin
uygulama noktası:
N
M O = Fd
1200 N ⋅ cm = (240 N )d
1200 N ⋅ cm
= 5 cm
d=
240 N
OB cos60° = 5 cm
OB = 10 cm
24 cm
N
24 cm
e) b, c ve d şıklarında elde edilen kuvvetler orjinal
kuvvet ile O noktasına göre eşit şiddetli ve yönlü
moment oluşturmaktadırlar. Fakat bu kevvetlerin
şiddeti, yönü ve tesir çizgileri farklı olduğu için
eşdeğer kuvvet değildirler.
24 cm
N
Örnek Problem 3.4
Dikdörtgen plaka A ve B noktalarından
duvara sabitlenmiştir ve CD teli ile
desteklenmektedir. Teldeki kuvvetin 200
N olduğu biliniyorsa, telin C noktasından
plakaya uyguladığı kuvvetin A noktasına
göre momentini hesaplayınız.
ÇÖZÜM:
F kuvvetinin A noktasına göre momenti
MA vektörel çarpım ile bulunur:
r
r
r
M A = rC A × F
r
r
r
M A = rC A × F
r
r
r
r r
rC A = rC − rA = (0.3 m )i + (0.08 m ) j
r
r
r
rC D
F = Fλ = (200 N )
rC D
r
r
r
− (0.3 m )i + (0.24 m ) j − (0.32 m )k
= (200 N )
0 .5 m
r
r
r
= −(120 N ) i + (96 N ) j − (128 N )k
r
r
r
i
j
k
r
M A = 0.3
0 0.08
− 120 96 − 128
r
v
r
r
M A = −(7.68 N ⋅ m ) i + (28.8 N ⋅ m ) j + (28.8 N ⋅ m )k
İki Vektörün Skaler Çarpımı
• İki vektör P ve Q nun skaler çarpım tanımı:
r r
P • Q = PQcosθ
• Scaler çarpım özellikleri:
r r r r
P•Q = Q• P
r r r
r r r r
P • (Q1 + Q2 ) = P • Q1 + P • Q2
r r r
P • Q • S = tanimsiz
(
)
• Kartezyen birim vektörlerin skaler çarpımı:
r
r
r r
r
r
r
r
P • Q = (Px i + Py j + Pz k )• (Qx i + Q y j + Qz k )
r r
r r
r r
r r
r r
v r
i •i =1 j • j =1 k •k =1 i • j = 0 j •k = 0 k •i = 0
r r
P • Q = PxQx + PyQy + Pz Qz
r r
P • P = Px2 + Py2 + Pz2 = P 2
İki Vektörün Skaler Çarpımı: Uygulamalar
• İki vektör arasındaki açı:
r r
P • Q = PQ cosθ = Px Qx + Py Q y + Pz Qz
cosθ =
Px Qx + Py Q y + Pz Qz
PQ
• Vektörün verilen eksendeki izdüşümü:
P’nin OL boyunca izdüşümü
POL = P cosθ
r r
P • Q = PQ cosθ
r r
P •Q
= P cosθ = POL
Q
• Birim vektör ile tanımlanmış bir eksen için:
POL
r r
= P•λ
= Px cosθ x + Py cosθ y + Pz cosθ z
Vektörlerin Üçlü Karişık Çarpımı
(
)
r r r
S • P × Q = skaler sonuc
• S, P ve Q vektörlerinin 6 değişik çarpımı eşit
şiddetlidir fakat işaretleri aynı değildir.
r r r
r r r
r r r
S • (P × Q ) = P • (Q × S ) = Q • (S × P )
r r
r r r
r r r
= − S • (Q × P ) = − P • (S × Q ) = −Q • (P × S )
r r r
S • (P × Q ) = S x (Py Qz − Pz Q y ) + S y ( Pz Qx − Px Qz )
+ S z (Pxy Qz − Py Qx )
Sx
Sy
Sz
= Px
Qx
Py
Qy
Pz
Qz
Bir Kuvvetin Verilen Bir Eksene Göre Momenti
• A noktasına uygalanan F kuvvetinin O noktasına
göre momenti MO :
r
r r
MO = r × F
• OL eksenine göre moment MOL, MO momentinin
OL ekseni üzerindeki izdüşümüdür:
M OL
r
(
r r r
r
= M 0Cosθ = M 01Cosθ = M 0 • λ = λ • M O = λ • r × F
λx
λy
λz
M OL = x
y
z
Fx
Fy
Fz
r
)
M x = yFz − zFy
• Momentin bileşenleri:
M y = zFx − xFz
M z = xFy − yFx
• Bir kuvvetin keyfi bir eksene göre momenti:
M BL
r
rA B
r
r
= λ •MB
r r
r
= λ • (rA B × F )
r r
= rA − rB
• Sonuç verilen eksendeki B noktasından bağımsızdır.
Örnek Problem 3.5
P kuvveti A küpüne F köşesinde
etkimektedir. P kuvvetinin
a) A noktasına göre,
b) AB kenarına göre,
c) AG köşegenine göre momentlerini
bulunuz.
d) AG ile FC.doğruları arasındaki dik
uzunluğu bulunuz.
• P kuvvetinin A noktasına göre momenti:
r
r
r
M A = rF A × P
r
r
r r
r
rF A = a i − a j = a (i − j )
r
r
r
r r
P = P (1 / 2 ) i + (1 / 2 ) j = ( P / 2 ) j − k
r
r r
r r
M A = a (i − j )× ( P / 2 ) j − k
(
(
(
)(
)
(
)
r
r r r
M A = aP / 2 i + j + k
)
• P kuvvetinin AB eksenine göre momenti:
M AB
r r
= i •MA
r
r r r
= i • aP / 2 i + j + k
(
M AB = aP / 2
)(
)
)
• P kuvvetinin AG köşegenine göre momenti:
r
r
M AG = λ • M A
r
r r
r
r rA G ai − aj − ak
1 r r r
(
=
=
i − j −k)
λ=
rA G
a 3
3
r
aP r r r
(
MA =
i + j +k)
2
1 r r r aP r r r
(
(
M AG =
i − j − k )•
i + j +k)
3
2
aP
(1 − 1 − 1)
=
6
M AG
aP
=−
6
• AG ile FC doğruları arsındaki dik mesafe:
r r P r r 1 r r r
P
(
(
(0 − 1 + 1)
P•λ =
j − k )•
i − j − k )=
2
3
6
=0
Bu nedenle, P vektörü AG.köşegenine diktir.
M AG
aP
=
= Pd
6
a
d=
6
Bir Kuvvet Çiftinin Momenti
• İki kuvvet F ve -F aynı şiddete, paralel tesir çizgisine
fakat zıt yönlere sahip ise kuvvet çifti oluştururlar
• Kuvvet çiftinin momenti:
r r r r
r
M = rA × F + rB × (− F )
r
r r
= (rA − rB ) × F
r r
= r×F
M = rF sin θ = Fd
• Kuvvet çiftinin moment vektörü seçilen koordinat
merkezinin yerinden bağımsızdır:
Serbest vektördür ve herhangi bir noktaya
uygulandığında aynı etkiyi oluşturu.
İki kuvvet çiftinin momentini aynı olması için:
• Paralel düzlemlere sahip olması gerekir
• Her iki kuvvet çiftinin oluşturduğu
momentlerin yönleri aynı olmalıdır.
• Ayrıca
F1d1 = F2 d 2
Kuvvet Çiftlerinin Toplanması
• Kuvvet çiftleri içeren P1 ve P2 kesişen
düzlemleri için:
r
r r
M 1 = r × F1 düzlem P1
r
r r
M 2 = r × F2 düzlem P2
• Vektörlerin bileşkesi de kuvvet çifti oluşturur:
r
r
r
r r r
M = r × R = r × (F1 + F 2 )
• Varignon theoremi kullanılırsa:
r r r r r
M = r × F1 + r × F2
r
r
= M1 + M 2
Kuvvet Çiftleri Vektörlerle Gösterilebilir
• Bir kuvvet çifti, kuvvet çiftinin oluşturduğu momentle
aynı şiddete ve yöne sahip vektörle gösterilebilir.
• Kuvvet çifti vektörleri vektörel toplama kurallarına uyarlar.
• Kuvvet çifti nektörleri bileşenlerine ayrılabilir.
• Kuvvet çifti vektörleri serbest vektördürler.
Uygulama noktası yerinin önemi yoktur.
Bir Kuvvetin O Noktasında
Bir Kuvvet ve Kuvvet Çiftine Çözümlenmesi
• Kuvvet vektörü F, O noktasına kaydırılırken sadece basit taşıma işlemi yapılmaz.
• O noktasında F kuvvetiyle aynı şiddete sahip zıt vektörler yerleştirilirse sistemde
değişikliğe neden olmaz.
• Bu üç kuvvet eşdeğer bir kuvvet ve kuvvet çifti ile yer değiştirebilir:
Kuvvet-Kuvvet çifti sistemi.
• F kuvvetinin A noktasından O’ noktasına kaydırılması farklı bir kuvvet
çiftinin toplamını gerektirir, MO’ :
r
r r
M O' = r ′ × F
• F kuvvetinin O’ noktalarına göre momentleri:
r
r r
r r r r r r r
M O ' = r '×F = (r + s ) × F = r × F + s × F
r
r r
= MO + s × F
• Kuvvet-Kuvvet çifti sisteminin O noktasından O’ noktasına taşınması, O
noktasındaki kuvvetin O’ noktasına göre momentinin toplamını gerektirir.
Örnek Problem 3.6
12 cm
12 cm
Şekildeki iki kuvvet çiftinin tek bir
kuvvet çifti için bileşenlerini bulunuz.
30 N
20 N
9 cm
20 N
9 cm
Çözüm
30 N
•
Verilen kuvvet çiftlerinin hesabını kolaylaştırmak için A
noktasına +x doğrultularında 20 N’luk iki kuvvet ilave
edilebilir. Böylece toplamı kolay olan 3 kuvvet çifti
oluşur.
• Alternatif olarak, iki kuvvetin uygulama noktası olduğu
için (bu kuvvetlerin momenti sıfır olacaktır), D noktasına
göre momentler hesaplanabilir.
• A noktasına 20 N şiddetli +x yönlerinde
iki kuvvet ilave edilirse:
12 cm
12 cm
30 N
20 N
20 N
20 N
9 cm
20 N
9 cm
30 N
• Üç kuvvet çifti:
M x = −(30 N )(18 cm ) = −540 N ⋅ cm
M y = +(20 N )(12 cm ) = +240 N ⋅ cm
M z = +(20 N )(9 cm ) = +180 N ⋅ cm
r
r
r
M = −(540 N ⋅ cm )i + (240 N ⋅ cm ) j
r
+ (180 N ⋅ cm )k
12 cm
12 cm
30 N
20 N
• Alternatif olarak, kuvvetlerin D
noktasına göre momenti hesaplanabilir:
• D noktasına göre sadece C ve E
noktalarındaki kuvvetlerin momentleri vardır.
9 cm
20 N
9 cm
30 N
r
r
r
r
M = M D = (18 cm ) j × (− 30 N )k
r
r
r
+ (9 cm ) j − (12 cm )k × (− 20 N )i
r
r
r
M = −(540 N ⋅ cm )i + (240 N ⋅ cm ) j
r
+ (180 N ⋅ cm )k
[
]
Kuvvet Sistemlerinin
Kuvvet ve Kuvvet Çiftine Çözümlenmesi
• Kuvvetler sistemi O noktasına göre bir kuvvet ve
kuvvet çiftine çözümlenebilir.
• Bilşeke kuvvet ve kuvvet çifti vektörleri:
r
r
R = ∑F
rR
r r
M O = ∑ (r × F )
• O noktasındaki kuvvet ve moment çifti O’ noktasına kaydırılırsa:
rR
rR r r
M O' = M O + s × R
• İki kuvvetler sistemi aynı kuvvet-kuvvet çiftine
çözümlenebiliyorsa eşdeğerdir.
Örnek Problem 3.8
Şekildeki kiriş için, kuvvetler sistemini
(a) A noktasındaki eşdeğer kuvvet-kuvvet çiftine
(b) B noktasındaki eşdeğer kuvvet-kuvvet çiftine ve
(c) tek bir kuvvete indirgeyiniz
Not: Mesnet tepkileri katılmayacağı için verilen kuvvet sistemi
etkisi altında kiriş dengede değildir.
a) Kuvvetleri A noktasına taşırsak:
r
r
R = ∑F
r
r
r
r
= (150 N ) j − (600 N ) j + (100 N ) j − (250 N ) j
r
r
R = −(600 N ) j
rR
r r
M A = ∑ (r × F )
r
r
r
r
= (1.6 i )× (− 600 j ) + (2.8 i )× (100 j )
r
r
+ (4.8 i )× (− 250 j )
r
rR
M A = −(1880 N ⋅ m )k
b) B noktasındaki eşdeğer kuvvet-kuvvet
çiftini bulmak için A noktasındaki
kuvvet-kuvvet çiftini kullanabiliriz.
r
r
R = −(600 N ) j
rR
rR r
r
M B = M A + rB A × R
r
r
r
= −(1880 N ⋅ m )k + (− 4.8 m )i × (− 600 N ) j
r
r
= −(1880 N ⋅ m )k + (2880 N ⋅ m )k
r
rR
M B = +(1000 N ⋅ m )k
Örnek Problem 3.10
Şekildeki dirseğe etki eden 3
kuvvet yerine A noktasına etkiyen
eşdeğer bir kuvvet-kuvvet çifti
bulunuz.
Kuvvet vektörlerinin A noktasına göre
yer vektörleri:
r
r
r
rB A = 0.075 i + 0.050k (m )
r
r
r
rC A = 0.075 i − 0.050k (m )
r
r
r
rD A = 0.100 i − 0.100 j (m )
• Kuvvetlerin bileşenleri:
r
r
r
FC = (1000 N )(cos 45 i − cos 45 j )
r
r
= 707 i − 707 j ( N )
r
r
r
FD = (1200 N )(cos 60 i + cos 30 j )
r
r
= 600 i + 1039 j ( N )
r
r
FB = (700 N )λ
r
r
r
r
r rE B 75 i − 150 j + 50k
=
λ=
rE B
175
r
r
r
= 0.429 i − 0.857 j + 0.289k
r
r
r
r
FB = 300 i − 600 j + 200k ( N )
• Eşdeğer Kuvvet:
r
r
R = ∑F
r
= (300 + 707 + 600 ) i
r
+ (− 600 + 1039 ) j
r
+ (200 − 707 )k
r
r
r
r
R = 1607i + 439 j − 507 k ( N )
• Kuvvet Çifti:
vR
r r
M A = ∑ (r × F )
r
i
r
r
rB A × F B = 0.075
r
k
r
j
r
r
0.050 = 30i − 45k
0
300 − 600 200
r
r
r
i
j
k
r
r
r
rC A × F c = 0.075 0 − 0.050 = 17.68 j
707
r
i
0
− 707
r
r
j
k
r
r
r
rD A × F D = 0.100 − 0.100 0 = 163.9k
600
1039
0
r
rR
r
r
M A = 30 i + 17.68 j + 118.9k
M=Fd
F
Civata sıkılması
d
F
Kapı açılması
d
Duvar
Menteşe
Duvar
Kapı
M=Fd