ELEKTRÝK -ELEKTRONÝK - BÝLGÝSAYAR MÜHENDÝSLÝÐÝ 10. ULUSAL KONGRESÝ
WIEN KÖPRÜ TABANLI KARI IK MODLU
KAOT K DEVRE MODEL (W-MMCC)
1
1
Recai Kılıç, 2Fatma Yıldırım
Erciyes Üniversitesi Müh. Fak. Elektronik Müh. Böl., 38039, Kayseri
2
Erciyes Üniversitesi Sivil Havacılık Y. O., 38039, Kayseri
[email protected]
[email protected]
Anahtar sözcükler: Wien Köprü Osilatör, Karı ık Modlu Kaotik Devre, Kaos
ÖZET
Bu çalı mada, do rusal ve do rusal olmayan
osilasyonlarla çalı an ara tırmacılar, ö renciler ve
bilim adamları için e itim amaçlı yeni bir devre
modeli sunulmu tur. Wien köprü tabanlı karı ık modlu
kaotik devre (Wien bridge-based Mixed-Mode
Chaotic Circuit, W-MMCC) olarak isimlendirilen
devre modeli, hem do rusal hem de do rusal olmayan
osilasyonları üreten bir yapıya sahiptir. Bu devre
yapısında, Wien köprü devre kısmından dolayı
sinüzoidal osilasyonlar gözlemlenmesinin yanı sıra,
hem otonom hem de otonom olmayan karı ık modlu
kaotik osilasyonların elde edilmesi de mümkün
olmaktadır. Devre, bu derece karı ık dinamikler
sergilemesine ra men donanım olarak basit bir yapıya
sahiptir. Devrede tek bir do rusal olmayan direnç
kullanılmı tır. Wien köprü tabanlı karı ık modlu
kaotik devrenin davranı ı, PSpice simülasyonları ile
do rulanmı tır.
1. G R
Son yirmi yılda ara tırmacılar, bilim adamları ve de
lisans ö rencileri için do rusal olmayan sistemlerle
özellikle de kaotik yapılarla ilgili literatürde e itim
amaçlı çalı malar yer almı tır. Kaosun varlı ını
göstermek ve ö rencilerin kaosu anlamasını
kolayla tırmak için Lonngren [1], bir deneysel
düzenek tanımlarken, Hamill [2], PSpice kullanarak
simüle edilmi 10 adet kaotik devrenin koleksiyonunu
içeren bir simülasyon çalı ması sunmu tur. Bu
çalı maların devamında Aissi [3], lisans ö rencilerine
elektronik derslerinde gösterilmesi amacıyla kaotik
devreler içeren e itim amaçlı bir çalı ma sunmu tur.
Literatürde yer alan ve yukarıda bahsedilen e itim
amaçlı çalı malara ek olarak bu bildiride, do rusal ve
do rusal olmayan osilasyonlarla ilgilenen bilim
adamları, ö renciler ve ara tırmacılar için yeni bir
e itim amaçlı devre modeli sunulmaktadır. Wien
köprü tabanlı karı ık modlu kaotik devre (W-MMCC)
olarak isimlendirilen devre modeli, hem do rusal hem
de do rusal olmayan osilasyonlar üreten bir yapıya
sahiptir ve bu devre, hem otonom hem de otonom
olmayan kaotik dinamikleri incelemek için e itim
amaçlı çok iyi bir modeldir. Hazırlanan bu çalı ma,
a a ıdaki bölümlerden olu maktadır: 2. bölümde,
334
Karı ık Modlu Kaotik Devre ve bu devrenin kaotik
dinamikleri tanıtılmı tır. 3. bölümde, Wien köprü
tabanlı karı ık modlu kaotik devre olarak adlandırılan
e itim amaçlı modelin devre yapısı ve davranı ı
simülasyon sonuçlarıyla birlikte tanımlanmı tır. Son
olarak 4. bölümde elde edilen sonuçlar tartı ılmı tır.
2. KARI IK MODLU KAOT K DEVRE
MODEL ve KAOT K D NAM KLER
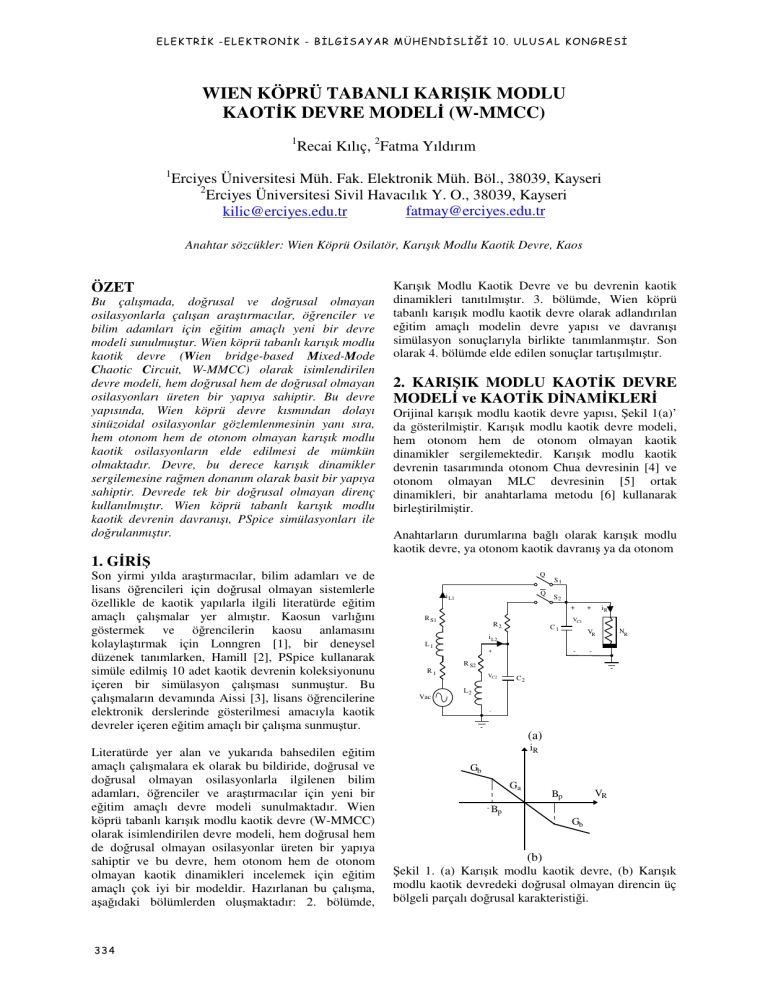
Orijinal karı ık modlu kaotik devre yapısı, ekil 1(a)’
da gösterilmi tir. Karı ık modlu kaotik devre modeli,
hem otonom hem de otonom olmayan kaotik
dinamikler sergilemektedir. Karı ık modlu kaotik
devrenin tasarımında otonom Chua devresinin [4] ve
otonom olmayan MLC devresinin [5] ortak
dinamikleri, bir anahtarlama metodu [6] kullanarak
birle tirilmi tir.
Anahtarların durumlarına ba lı olarak karı ık modlu
kaotik devre, ya otonom kaotik davranı ya da otonom
Q
Q
i L1
S1
S2
+
R S1
R2
R1
Vac
C1
-
+
iR
VR
i L2
L1
+
VC1
NR
-
R S2
VC2
C2
L2
-
(a)
iR
Gb
Ga
VR
Bp
- Bp
Gb
(b)
ekil 1. (a) Karı ık modlu kaotik devre, (b) Karı ık
modlu kaotik devredeki do rusal olmayan direncin üç
bölgeli parçalı do rusal karakteristi i.
ELEKTRÝK -ELEKTRONÝK - BÝLGÝSAYAR MÜHENDÝSLÝÐÝ 10. ULUSAL KONGRESÝ
olmayan kaotik davranı sergilemektedir. Anahtarların
durumları, S1-ON ve S2-OFF oldu unda karı ık
modlu kaotik devre modeli, otonom olmayan kaotik
MLC devre yapısına [5] dönü ür. Bu durumda devre,
iki adet birinci dereceden otonom olmayan
diferansiyel denklem takımı ile tanımlanmaktadır:
C1
L1
di L1
dt
dVC1
= i L1 − f (VR )
dt
(1)
= − i L1 (R1 + RS1 ) − VC1 + A sin (wt )
(2)
Burada (A), ekil 1(a)’ daki Vac harici periyodik
i aretin genli ini ve (w) da açısal frekansını temsil
etmektedir. Harici i aretin genli i (A), kaotik de i im
(bifurcation) parametresi olarak kullanılmaktadır. Bu
genlik de erinin sıfırdan yukarıya do ru artırılmasıyla
dallanma
ve
kaos
olayı
sistem,
de i ik
sergilemektedir.
ekil 1(a)’ daki devrede anahtarların durumları S1OFF ve S2-ON oldu unda devre, otonom Chua
devresine dönü mektedir [4]. Bu durumda devre, üç
adet birinci dereceden otonom diferansiyel denklem
takımı ile tanımlanmaktadır:
di L 2
(3)
L2
= −VC 2 − i L 2 ⋅ R S 2
dt
dV
1
(4)
(VC 2 − VC1 )
C2 C 2 = i L 2 −
dt
R2
C1
dVC1
1
( VC 2 − VC1 ) − f (VR
=
dt
R2
)
3. WIEN KÖPRÜ TABANLI KARI IK
MODLU KAOT K DEVRE MODEL
E itim amaçlı olarak dü ünülen karı ık modlu kaotik
devrenin yeni gerçekle tiriminde, ekil 1(a)’ daki
devrenin pasif LC rezonatörü, aktif Wien köprü
tabanlı RC konfigürasyonu ile de i tirilmi tir. Wien
köprü tabanlı karı ık modlu kaotik devre, ekil 3’ de
lk olarak, statik anahtarlama
gösterilmi tir.
kullanılarak devrenin statik performansı gösterilecek
ve do rulanacaktır. Anahtarların durumları, S1-ON ve
S2-OFF oldu unda orijinal karı ık modlu kaotik devre
yapısındaki otonom olmayan aynı kaotik devre kısmı
elde edilir. Bundan dolayı bu durumda devre, orijinal
karı ık modlu kaotik devredeki gibi iki adet birinci
dereceden otonom olmayan diferansiyel denklem
takımı ile tanımlanmaktadır:
(5)
ekil 1(a)’ daki devrede R2 direnç de eri kaotik
de i im parametresidir ve bu direnç de erinin 2000
Ω’ dan 0 Ω’ a do ru azaltılmasıyla devre, de i ik
dallanma ve kaos olayı sergilemektedir. Burada, (1) ve
(5) ba ıntısında verilen f(VR) ifadesi, parçalı do rusal
ekil 1(b)’ de grafiksel olarak
bir fonksiyondur ve
gösterilmi olup a a ıdaki gibi tanımlanmaktadır:
(6)
iR = f (VR ) =GbVR +0.5⋅(Ga −Gb ) × VR + Bp − VR −Bp
(
Karı ık modlu kaotik devre modelinin yukarıdaki
statik çalı masına ek olarak ekil 1(a)’ daki S1 ve S2
analog anahtarların giri lerine iki e lenik Q ve Q
kontrol i aretleri sürekli uygulanarak, karı ık modlu
kaotik devrenin kaotik dinami i elde edilmektedir.
Karı ık modlu kaotik devrede kontrol i areti olarak
periyodik i aretler kullanılabilece i gibi periyodik
olmayan i aretler de kullanılabilir. Dinamik çalı ma
modu için karı ık modlu kaotik devrenin davranı ı
ekil 2’ de gösterilmektedir. Burada, darbe süreleri 5
msn olan Q ve Q kontrol i aretleri kullanılmı tır.
)
Burada, Ga ve Gb, sırasıyla iç ve dı bölgelerdeki
e imler olup, ±BP kırılma noktalarını belirtmektedir.
Do rusal olmayan direnç, Ga=-0.76 mS, Gb=-0.41 mS
ve ±BP=±1.0 V parametrelerini verecek ekilde [7]’
deki devre topolojisi kullanılarak gerçekle tirilmi tir.
C1
di L1
L1
dt
dVC1
= i L1 − f (V R )
dt
(7)
Burada (A), ekil 1(a)’ daki Vac harici periyodik
i aretin genli ini ve (w) da açısal frekansını temsil
etmektedir. Harici i aretin genli i (A), kaotik de i im
(bifurcation) parametresi olarak kullanılmaktadır. Bu
genlik de erinin sıfırdan yukarıya do ru artırılmasıyla
sistem de i ik dallanma ve kaos olayı sergilemektedir.
Bu otonom olmayan devre kısmı için devre
parametreleri, C1=10 nF, L1=18 mH, R1=1340 Ω,
RS=12.5 Ω, A=0.15 V ve harici i aret kayna ının
frekansı 8890 Hz olarak belirlenmi tir. Bu çalı ma
modunda Wien köprü tabanlı karı ık modlu kaotik
devrenin otonom olmayan kaotik davranı ı, Wien
Q
Q
i L1
S1
S2
+
RS
R2
C1
+
L1
R3
VC2
R1
C2
R6
Vac
-
ekil 2. ekil 1(a)’ daki karı ık modlu kaotik devrenin
kaotik davranı ı.
(8)
= − i L1 (R1 + RS ) − VC1 + A sin (wt )
C3
Vout
VR
-
+
+ iR
VC1
NR
-
VC3
R4
R5
ekil 3. Wien köprü tabanlı karı ık modlu kaotik
devre.
335
ELEKTRÝK -ELEKTRONÝK - BÝLGÝSAYAR MÜHENDÝSLÝÐÝ 10. ULUSAL KONGRESÝ
köprü devresinin sinüzoidal formdaki çıkı osilasyonu
ve kaotik çift çeker yapısı, sırasıyla ekil 4(a), 4(b) ve
4(c)’ de gösterilmektedir. Bu anahtarlama modunda,
C1 kapasitörü üzerindeki voltaj otonom olmayan
kaotik osilasyon olarak gözlenirken, Wien köprü çıkı
sinüzoidal
osilasyonlar
dü ümünde
gözlemlenmektedir. Bundan dolayı hem kaotik hem de
periyodik osilasyonlar, bu osilatör yapısında e
zamanlı olarak gözlemlenebilmektedir. Anahtarların
durumları, S1-OFF ve S2-ON oldu unda kaotik çift
çeker yapısını sergileyen otonom Wien köprü tabanlı
Chua devresi [8] elde edilmektedir. Burada Op-Amp
(VOA) kullanılarak gerçekle tirilen Wien köprü
osilatörünün kazancı, K = 1 + R4 ’ dir. Bu durumda
R5
devre, üç adet birinci dereceden otonom diferansiyel
denklem takımı ile tanımlanmaktadır:
(a)
C3
dVC 3
R
1
= − 4 VC 2 − VC 3
dt
R3 R5
R3
C2
dVC 2
1
1
1
= VC1 −
VC 2 + VC 3
dt
R2
RX
R3
(10)
C1
dVC1
1
=
( VC 2 − VC 1 ) − f ( V R
dt
R2
(11)
(9)
)
Burada f(VR), (6) ba ıntısındaki gibi tanımlanmaktadır
ve,
RX =
R2 R3 R6 R5
R2 ( R3 R5 − R6 R4 ) + R3 R6 R5
(12)
olarak ifade edilmektedir.
C1 kapasitörü ve NR do rusal olmayan direnci, otonom
ve otonom olmayan çalı ma modları için karı ık
modlu kaotik devrede ortak elemanlar oldu undan bu
elemanların parametre de erlerine göre Wien köprü
tabanlı RC konfigürasyonunun devre parametreleri
belirlenmektedir. Devrenin çift çeker yapısını
sergilemesi için devre parametreleri, C1=10 nF,
C2=C3=800 nF, R3=R5=R6=100 Ω, R4=207 Ω ve
R2=1.525 Ω olarak belirlenmi tir. C de erleri ve R
de erleri e it seçilerek (C2=C3=C0, R3=R6=R0), Wien
köprü osilatörde osilasyonların ba laması için
devrenin voltaj kazancı K, nominal de erinin (K=3)
biraz üzerinde seçilmi tir (K=3.07). Wien köprü
tabanlı karı ık modlu kaotik devrenin otonom kaotik
dalga formu ve kaotik çift çeker yapısı sırasıyla ekil
5(a) ve 5(b)’ de gösterilmi tir. Bu çalı ma modunda
tasarlanan devre, R2 de i im parametresinin 1250 Ω1850 Ω de erleri arasında farklı periyodik ve kaotik
davranı lar sergileyebilmektedir.
(b)
(a)
(c)
ekil 4. Otonom olmayan çalı ma modunda Wien
köprü tabanlı karı ık modlu kaotik devrenin
simülasyon sonuçları, (a) Otonom olmayan kaotik
dinamik, (b) Wien köprü devresinin çıkı osilasyonu,
(c) (VC1-IL1) düzleminde kaotik çift çeker gösterimi.
336
(b)
ekil 5. Otonom çalı ma modunda Wien köprü tabanlı
karı ık modlu kaotik devrenin simülasyon sonuçları,
(a) C1 kapasitörü üzerindeki voltajın kaotik dalga
formu, (c) (VC1-VC2) düzleminde kaotik çift çekerli
yapının gösterimi.
ELEKTRÝK -ELEKTRONÝK - BÝLGÝSAYAR MÜHENDÝSLÝÐÝ 10. ULUSAL KONGRESÝ
Q
Q
i L1
4. SONUÇ
S1
S2
+
RS
Q S
3
L1
R2
C1
R3
+
VC2
R1
C2
R6
Vac
-
+
C3
V out
+
VC1
VR
-
iR
NR
-
VC3
-
R4
R5
ekil 6. S3 anahtarı ilave edilerek modifiye edilen
Wien köprü tabanlı karı ık modlu kaotik devre.
Wien köprü tabanlı karı ık modlu kaotik devrenin
dinamik performansını de erlendirmek amacıyla statik
performans gösterildikten sonra iki e lenik kare dalga,
Q ve Q , orijinal karı ık modlu kaotik devredeki gibi
anahtarlama i leminin sürekli olarak devam etmesi
için, ekil 3’deki S1 ve S2 analog anahtarlarının
giri lerine uygulanmalıdır. Her bir kare dalganın darbe
geni li i ve periyodu sırasıyla 5 msn ve 10 msn olarak
seçilmi tir. Bu dinamik çalı ma modunda orijinal
karı ık modlu kaotik devrenin davranı ına benzer bir
karı ık modlu kaotik dinamik gözlemlemek amacıyla,
S2 anahtarı ile e zamanlı olarak çalı an analog S3
anahtarı, ekil 6’da gösterildi i gibi Wien köprü
tabanlı karı ık modlu kaotik devreye eklenmi tir.
Wien köprü tabanlı karı ık modlu kaotik devre, S3
anahtarı olmaksızın otonom olmayan aynı kaotik
davranı ı sergilerken otonom olmayan moddan
otonom moda geçi sırasında Wien köprü devrenin
osilasyonundan dolayı Wien köprü tabanlı karı ık
modlu kaotik devre, otonom kaotik davranı ı
sergilememektedir. Bu yüzden, otonom olmayan
modda S2 anahtarı ile e zamanlı olarak çalı an S3
anahtarı, Wien köprü devresinin çıkı osilasyonunu
önlemektedir. Önerilen Wien köprü tabanlı karı ık
modlu kaotik devrenin karı ık modlu kaotik dalga
formu, ekil 7’de gösterilmi tir.
Bu çalı mada e itim amaçlı yeni bir Wien köprü
tabanlı karı ık modlu kaotik devre modeli önerilmi tir.
PSpice simülasyon sonuçları, Wien köprü tabanlı RC
konfigürasyonu kullanılarak gerçekle tirilen karı ık
modlu kaotik devrenin, orijinal karı ık modlu kaotik
sergiledi ini
devrenin
kaotik
davranı ları
do rulamaktadır. Karı ık modlu kaotik devrenin bu
yeni gerçekle tirimi, do rusal ve do rusal olmayan
osilasyonlarla çalı mak için iyi bir prototip
olu turmaktadır.
Karı ık modlu kaotik devrede, Wien köprü devresinin
kullanımı, mevcut parametrelere ek olarak yeni devre
parametre de i imleri içermektedir. Bu yüzden,
karı ık modlu kaotik devrenin bu yapıdaki
gerçekle tirimi, sadece basit bir tasarıma sahip
olmakla kalmayıp aynı zamanda olası kaotik
uygulamalarında
geni
parametre
haberle me
de i ikleri ile daha fazla güvenilirlik sa lama
potansiyeline sahiptir. Ayrıca karı ık modlu kaotik
devrede Wien köprü tabanlı RC konfigürasyonu
kullanılarak indüktör sayısı azaltılmaktadır.
KAYNAKLAR
[1] Lonngren K.E., Notes to accompany a student
laboratory experiment on chaos, IEEE Trans. on
Education, 34, (1), 1991.
[2] Hamill D.C., Learning about chaotic circuits with
SPICE, IEEE Trans. on Education, 36, (1), pp.123128, 1993.
[3] Aissi C., Introducing chaotic circuits in an
undergraduate electronic course, Proceedings of
the 2002 ASEE Gulf-Southwest Annual
Conference, Lafayette, USA, 2002.
[4] Chua L.O., Wu C.W., Huang A., and Zhong G.A.,
Universal circuit for studying and generating
chaos, IEEE Trans. Circuits&Syst., CAS-40, (10),
pp.732-745, 1993.
[5] Murali K., Lakshmanan M., and Chua L.O.,
Bifurcation and chaos in the simplest dissipative
non-autonomous
circuit,
Int.
J.
of
Bifurcations&Chaos, 4, (6), pp.1511-1524, 1994.
[6] Kılıç R., Alçı M. and Tokmakçı M., Mixed-mode
chaotic circuit, Electronic Lett., 36, (2), pp.103104, 2000.
[7] Kennedy M.P., Robust Op-Amp realization of
Chua’s circuit, Frequenz, 46, pp.66-80, 1992.
[8] Morgül Ö., An RC Realization of Chua’s circuit
family, IEEE Trans. Circuits& Syst-I., 47, (9),
pp.1424-1430, 2000.
ekil 7. Wien köprü tabanlı karı ık modlu kaotik
devrenin kaotik davranı ı.
337