Tork ve Denge - Nihat Bilgin Yayıncılık

11. SINIF
SORU BANKASI
1. ÜNİTE: KUVVET VE HAREKET
8. Konu
TORK VE DENGE
TEST ÇÖZÜMLERİ
8
Tork ve Denge
Test 1 in Çözümleri
1.
(–)
(+)
F
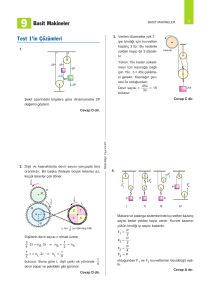
3. F1 = k · x1
r
P = k · x1
x1 =
P
k
F2 = k · x2
2P = k · x2
2P
k
F3 = k · x3
O
r
F
2F
x1
2P
P
x3
x2 =
P
P
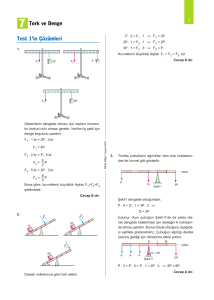
O noktasına göre tork alalım. Toplam tork;
P = k · x3
τ = F · 0 + F · r – 2F · r
x3 =
τ = –F · r
P
k
F4 = k · x4
bulunur.
P · sin37° = k · x4
P · 0, 6
x4 =
7°
k
in3
P·s
Buna göre, yaylardaki uzama miktarlarının büyüklük ilişkisi;
x2 > x1 = x3 > x4
şeklinde olur.
2.
Nihat Bilgin Yayıncılık©
Yanıt A dır.
F1
x2
x4
37°
Yanıt B dir.
O
F2
4.
F3
T
Birim karelerin bir kenar uzunluğunu F alarak F 1 ,
F 2 , F 3 kuvvetlerinin O noktasına göre torklarını
alalım.
30°
L
K
P
τ1 = F · 2
G
N
M
τ2 = F · 2 · 2
2
τ2 = F
τ3 = F · 3
τ3 = 3F
τ3 > τ1 > τ2 büyüklük ilişkisi vardır.
P
L noktasına göre tork alınırsa;
T · 4 · sin30° = G ·
4P · 4 ·
Yanıt B dir.
5
+P·3
2
5G
1
=
+ 3P
2
2
G = 2P bulunur.
Yanıt D dir.
TORK VE DENGE
5.
7.
T1
37°
Şekil I
3
53°
T3
T1
T2
37°
T1x
ip
53°
T3x
30°
L
K
6P
P 1 = 30 N
T2
T1x = T2
Şekil II
2P
T1 · cos37° = T2
T1 · 0,8 = T2
4P
T1 . sin30° · 6 = 6P · 3
T1 = 6P
T2 · 2 = 4P · 2 + 2P · 4
T2 = 8P
T1
T2
=
3
4
olur .
Yanıt A dır.
6.
Nihat Bilgin Yayıncılık©
6P
=
T2
8P
5
T
4 2
T3x = T2
T1 =
T3 · cos53° = T2
T3 · 0,6 = T2
T1
P2
ip
5
T
3 2
Buna göre, iplerdeki gerilme kuvvetleri T3 > T1 > T2
şeklinde sıralanır.
T3 =
Yanıt E dir.
T2
T1
T2·sin37°
30 N
45°
45°
8.
P2
P1
N
P
=
sin 90 °
sin 143 °
P
N=
0, 6
N=
Bir sistem dengede ise yatayda sağa doğru olan
kuvvetler sola doğru olan kuvvetlere eşittir. Buradan;
T2·sin37° = P1
T2 ·
3
= 30
5
T2 = 50 N bulunur.
Yanıt D dir.
53°
T
5
P
3
Y noktasına göre
tork alınırsa;
N
ip
143°
X
N·1=T·2
5
P=T·2
3
6
P
olur.
=
5
T
Y
N
P
Yanıt C dir.
4
Ünite 1
Kuvvet ve Hareket
9. Uzun çubuğun tepki kuvvetine
N diyelim N in olduğu yere göre
P
tork alırsak T1 =
olur.
2
P
Aynı zamanda N =
olacaktır.
2
11.
T1
N
3
P
Şekil I
P
T2
Şekil II
Şekil II de destek noktasına göre tork alalım;
T2 · 4 = 3P · 2 + N · 2
P
4T2 = 6P +
·2
2
7
T2 = P
4
P
T1
2
=
7
T2
P
4
T1
T2
=
2
7
GK = P · sin3a
GL = P · sin2a
GM = P · sina
Buna göre GK > GL > GM olur.
M
Yanıt E dir.
bulunur.
Yanıt B dir.
10.K yüzeyinin küreye tepkisi TK, L yüzeyinin küreye
tepkisi TL aşağıda şekil üzerinde gösterilmiştir. TL
nin düşey bileşeni P ye eşit olup sabittir.
P
Nihat Bilgin Yayıncılık©
P
P ağırlıklı cismi tutan ip-
lerdeki gerilme kuvvetleri
de P dir. Bu P kuvvetinin
düşey bileşeni K, L, M cisimlerinin
ağırlıklarına
eşittir.
N
K
L
3P
2
12.Şekil I deki çubuğun ağırlık merkezi destek noktasıdır.
L
K
TL · sinq = P yazabiliriz.
Şekil I
K
G
L
TL
T
53°
TK
q
L
Şekil II
P
q
K
37°
L yüzeyi ok yönünde döndürüldükçe q açısı artar.
Bu durumda sinq artacağı için TL azalmalıdır.
TL nin yatay bileşeni TK ya eşittir.
TL · cosq = TK
q açısı arttıkça cosq azalır. Ayrıca TL de azaldığına göre TK azalmalıdır.
Yanıt D dir.
yatay
G
Şekil II deki K dönme noktasına göre tork alınırsa;
G · 2 · cos37° = T · 5 · cos37°
G·2=T·5
2
T
=
olur.
5
G
Yanıt D dir.
TORK VE DENGE
13.K yüzeyinin tepki kuvveti NK, L yüzeyinin tepki kuvveti NL şekildeki gibidir.
5
15.
K
A
yatay
NL
G
L
F = 10 N
NK
yatay
A noktasına göre tork alınırsa;
G = 10 2 N
yatay
45°
Lami teoremini uygularsak;
F·1=G·1
G = 10 N bulunur.
Yanıt B dir.
NL
sin 90 °
=
NL =
G
sin 4 5 °
10 2
2
2
NL = 20 N olur.
14.
Nihat Bilgin Yayıncılık©
Yanıt B dir.
v2F
16.
2F
A
T
T
53°
143°
fs
127°
yatay
A
P
F
2F
P
T
=
sin 143 °
sin 127°
Yalnız F kuvvetinin A noktasına göre torku;
τ=F·2
dir. Tüm kuvvetlerin A noktasına göre toplam torku;
R x = 2 F ·1 +
2 F · 2 2 – 2 F ·1 + F · 2
P
T
=
0, 6
0, 8
T=
A cisminin dengede kalması için T ip gerilmesi,
fs sürtünme kuvvetine eşit olmalıdır.
T = fs =
Rx = 6F
Rx = 3x
bulunur .
Yanıt E dir.
4
P
3
4
P
3
Yanıt A dır.
6
Ünite 1
Kuvvet ve Hareket
17.Desteğin sol tarafındaki 4 parçanın ağırlığı 20 N
olup şekildeki gibi gösterebiliriz.
19.K duvarının tepkisi F1 ,
F kuvvetinin yatay bileşenine eşittir.
O
N
M
20 N
P=10 N
K
T
10 · 1 + 20 · 2 = 5 · n ·
n
2
n=
F1 = 16 N
L duvarının tepkisi ile
düşey
ağırlığın toplamını F
kuvvetinin düşey bileşeni dengeler. F2, L duvarının
tepkisi olmak üzere;
F2 + G = F · sin37°
F2 + 10 = 20 · 0,6
n2 = 20
20
4 < n < 5 olduğu için alev KL arasına geldiği zaman
kalas bir süre için yatay konuma gelir.
Yanıt D dir.
F = 20 N
37°
37°
F1 = F · cos37°
yatay
Alev destekten n bölme uzağa geldiği zaman, kalasın bir süre için yatay dengede kaldığını varsayarak destek noktasına göre tork alalım.
yatay
F1
alev
L
L
F2 = 2 N bulunur.
Buradan;
F1
K
G = 10 N
F2
F1
F2
=
16
2
=8
olur .
Nihat Bilgin Yayıncılık©
Yanıt E dir.
18.
T2
L
T1
O
20.Sistem dengede olduğuna
göre F + T = P olmalıdır.
Yani P en büyüktür. Ayrıca
P ağırlık merkezine göre
tork alınırsa;
K
G
Çubuğun ağırlık merkezi olan O noktasına göre tork
alırsak T1 ve T2 kuvvetlerinin oranını buluruz.
T1 · 3 = T2 · 1
1
olur.
=
T2
3
Yanıt A dır.
F·1=T·2
yer
P
T1
T
F = 2T bulunur.
F
Buna göre, P > F > T büyüklük ilişkisi vardır.
Yanıt B dir.
TORK VE DENGE
Test 2 nin Çözümleri
3. T · 3 = P · 5 · cos53°
1.
yatay
T1 30°
30°
3T = P · 5 · 0,6
T = P olur.
T
P
T3
53°
yatay
T2
P
T1
sin 90 °
=
T1 =
T1
T2
7
P
Yanıt A dır.
T2
sin 150 °
T2
4.
0, 5
yatay
=2
olur .
2T1
T3
T2
T1
Yanıt E dir.
yatay
Y
X
Nihat Bilgin Yayıncılık©
P
Aynı ip üzerinde oldukları için T1 = T2 olmalıdır.
T1 ve T2 ip gerilme kuvvetlerinin bileşkesi tam ortadan alınır. P ağırlık merkezine göre tork alalım.
2T1 · 1 = T3 · 3
2T1 = 3 · T3
Buna göre, T1 = T2 > T3 büyüklük ilişkisi yazılır.
Yanıt D dir.
2.
T3
yatay
T2
45°
5.
X
Y
T1
yatay
Bir cisim dengede ise cisme etki eden kuvvetlerin
yatay bileşenlerinin vektörel toplamı sıfır olmalıdır.
T3 · cos45° = T1
Bu durumda T3 > T1 olur.
Ağırlık merkezine göre tork alalım;
T3 · sin45° = T2
Bu durumda T3 > T2 olur.
cos45° = sin45° olduğundan,
T1 = T2 olur.
T
F
2F
F
yatay
2P
İp gerilmelerine F diyelim. F kuvvetlerinin bileşkesi şekildeki 2F dir. 2F nin olduğu noktaya göre tork
alalım. Buradan;
Yanıt A dır.
2P ·
3
7
=T·
2
2
6
T = P olur.
7
Yanıt D dir.
8
Ünite 1
Kuvvet ve Hareket
6. F2 nin yatay ve düşey bileşenleri şekildeki gibi F olsun.
9.
I
II
K
τ1 = F1 · 0
τ1 = 0
τ2 = F · 3 + F · 2
τ2 = 5F
τ3 = 2F
τ1, τ2 , τ3 torklarının büyüklük sıralaması τ2 > τ3 > τ1 olur.
su
su
F3
F
F1
F2
L
K
F
Buna göre,
Yanıt C dir.
II. Kaba atılan 30 gram kütleli cismin özkütlesi
2 g/cm3 ise hacmi;
m
d
30
V=
= 15 cm3 tür.
2
Suyun özkütlesi 1 g/cm3 olduğundan hacmi ve kütlesi birbirine eşittir.
7. K dönme noktasına
göre tork alınırsa;
K
F·2+P·
P
F=
4
F
3
= 2P · 1
2
olur.
2P
4P
P
Yanıt E dir.
Nihat Bilgin Yayıncılık©
düşey
V=
I nolu kefedeki ağırlaşma 30 – V gram,
II nolu kefedeki ağırlaşma 30 – 15 = 15 gram,
Boş kefede biriken su kütlesi 15 + V gram olur.
Destek noktasına göre tork alınırsa;
(30 – V) · 2 = 15 · 2 + (15 + V) · 1
V = 5 cm3
bulunur. Buna göre I. kaba atılan cismin özkütlesi;
dcisim =
m
V
30
dcisim =
= 6 g/cm3 olur.
5
Yanıt D dir.
10.
T1
T2
A
yatay
8.
X
L
X
P
Y
Z
K
L
M
T3
P
Y
K
P
M
P ağırlıklı küre L ipinin sağ tarafında iken K ipi, küre
L ipinin sol tarafına geçince L ipi dengeyi sağlayacağı için M ipi kesilirse yatay denge bozulmaz.
Yanıt C dir.
İlk durumda türdeş çubuğun tüm ağırlığını T1 ip gerilmesi taşırken T2 ve T3 gerilmeleri sıfırdır. Çubuğun XZ kısmı kesilip atılırsa; ağırlık merkezi T2
ipinin bağlı olduğu noktaya kayacağından T2 artar,
T1 ve T3 sıfır olur.
Yanıt D dir.
TORK VE DENGE
11.
T1
K
13.
düşey
T
9
L
T2
2a
P
P
Düşey denge koşulundan;
T1 = 2P + T2 ....................... (1)
yazabiliriz. T1 ipinin bağlı olduğu noktaya göre tork
alırsak;
2P · 2 = T2 · 2
T2 = 2P ............................. (2)
T · 2 = 24 · 1
(2) nolu denklem (1) nolu denklemde yerine yazılırsa;
T = 12 N bulunur.
T1 = 4P bulunur.
K noktasındaki P ağırlıklı araba L noktasına götürülürse çubuğun ağırlığı ile dengelenir. Bu durumda
Tʹ2 = 0 ve Tʹ1 = 2P olacağından T1 ve T2 azalır.
Yanıt B dir.
a
37°
yatay
24 N
T ip gerilmesi ve levhanın ağırlığı aynı doğrultudadır. Ağırlık merkezinin dönme noktasına uzaklığı 1
br, T ninki de 2 br dir. Buna göre, dönme noktasına
göre tork alırsak;
Nihat Bilgin Yayıncılık©
Yanıt B dir.
14.
T2
12.
X
T1
Y
O1
N
O2
G
4P
4P
O1 , O2 noktalarının üzerinde bulunduğu düşey
doğrultuya göre tork alırsak, desteğin tepkisi;
T1 ve T2 gerilmelerinin bulunduğu iplerin düzgün
türdeş altıgen levhanın ağırlık merkezine uzaklıkları sırasıyla 2 birim ve 1 birimdir. Ağırlık merkezine
göre tork alınırsa;
destek
4P · 2 + 4P · 4 = N · 6
N = 4P bulunur.
T1 · 2 = T2 · 1
T1
T2
=
1
bulunur.
2
Yanıt B dir.
Yanıt D dir.
10
Ünite 1
Kuvvet ve Hareket
15.
17.
T
2T
T3
T1
53°
yatay
T
T
120°
T
T
T2
P
P1
T3 · cos53° = T2
T3 · 0,6 = T2
3
· T3 ......................... (1)
5
yazabiliriz. Ağırlık merkezine göre tork alınırsa;
T1 · 2 = T3 · sin53° · 2
4
T ....................... (2)
5 3
(1) ve (2) denklemlerini taraf tarafa bölelim.
T1
4
bulunur.
=
T2
3
Yanıt E dir.
T2 =
Şekil I incelenirse;
P1 = T
Şekil II incelenirse;
P2 =
Buna göre 2P1 =
Şekil II
2T
2 P2 olarak bulunur.
Yanıt E dir.
T1 =
Nihat Bilgin Yayıncılık©
Şekil I
Türdeş çubuk dengede olduğuna göre, bir yöndeki
kuvvetler aksi yöndeki kuvvetlere eşittir. Bunu yatay
doğrultu için kullanırsak;
P2
18.
O
37°
53°
16.
P3
30°
P2
P
53°
P1 60°
G
60°
O
60°
O
60°
53°
P
O
Aynı çubuk üç farklı şekilde dengede kaldığına göre
P1, P2, P3 ağırlıklarının torku eşittir.
P1 · sin60° = P2 = P3 · sin30°
Bu durumda ağırlıkların büyüklük ilişkisi;
P3 > P1 > P2 olur.
O dönme noktasına göre tork alınırsa;
G · 2 · sin53° + P · 4 · sin53° = P · 4
Yanıt D dir.
G · 2 · 0,8 + P · 4 · 0,8 = 4P
1,6 G = 0,8 P
G
1
olur.
=
P
2
Yanıt E dir.
TORK VE DENGE
19.
F
N
M
X
3G
3G
Y
Alttaki çubuğun ağırlık merkezi X desteğinden 1 birim, Y den 2 birim uzaktadır. Buna göre, çubuğun
ağırlığının G kadarını Y desteği, 2G kadarını da X
desteği dengeler.
Üstteki çubuğun dönebilmesi için F = 3G kadar kuvvete ihtiyaç vardır. Bu anda üstteki çubuktan dolayı
Y desteğine düşen kuvvet 6G, X desteğine düşen
kuvvet sıfırdır.
Bu durumda,
FY
FX
FY
=
2G + 0
G + 6G
=
2
7
bulunur .
Yanıt A dır.
Nihat Bilgin Yayıncılık©
FX
11
12
Ünite 1
Kuvvet ve Hareket
3.
Test 3 ün Çözümleri
düşey
ip
1. T1 in düşey bileşeni
P ağırlığına eşit olup
sabittir. Bu durumda ip
K dan L ye getirilirken
düşey bileşenin değişmemesi için T1 azalmalıdır.
L
K
37°
T
T1
T3
a
53°
P·cos37°
P
T2
Dönme noktasına göre tork alınırsa;
P
T2, P ağırlığını dengelediği için değişmez. T1 in yatay bileşeni T3 gerilmesine eşittir. İp K dan L ye getirilince T1 in yatay bileşeni sıfır olacağından T3 azalmış olur.
T · 1 = P · 2 · cos37°
T = P · 2 · 0,8
T=
8
P olur.
5
Yanıt C dir.
Nihat Bilgin Yayıncılık©
Yanıt D dir.
4.
2.
R
T1
ip
T
P
4G
Şekil I
ip
yatay
K
Denge şartına göre; T nin yatay bileşeni F ye, düşey bileşeni de P nin yarısına eşit olur.
T · cos30° = F
T · sin30° =
P
2
Bu durumda, P = T > F olur.
Yanıt A dır.
P
Şekil II
4G
Çubuğun ağırlığına 4G diyelim. T1 nin ağırlık merkezine uzaklığı 1 birim, T2 nin de 3 birim olduğu
için;
P
30˚
R
30˚
F
T3
T2
T1 = 3G
T2 = G olur.
Benzer düşünceyi Şekil II’de uygularsak, T3 = 3G
zeminin tepkisi de G olur. Bu durumda T1 = T3 > T2
olur.
Yanıt D dir.
TORK VE DENGE
5.
13
7.
k3 = 4k
T1
X
Y
X
Y
k1 = k
k2 = k
P1
P2
GY = P
Dönme noktasına göre tork alınırsa, P1 = 3P2 eşitliği yazılır. Yani P2 = P ise P1 = 3P olur. Buna göre
yayların uzama miktarları;
3P = k · x1
x1 =
3P
k
P = k · x2
P
x2 =
k
4P = 4k · x3
1. şekilde desteğe göre tork alınırsa;
2P · 2 = T1 · 4
T1 = P
2. şekilde desteğe göre tork alınırsa;
T2 · 1 = P · 1 + 2P · 3
P
k
olarak bulunur. Yayların uzama miktarlarının büyüklük ilişkisi x2 = x3 < x1 olur.
T2 = 7P
olarak bulunur. Buna göre T1 ve T2 ip gerilmeleri
arasında 7T1 = T2 ilişkisi vardır.
Yanıt B dir.
8.
F
6.
T1 = P
GX = 2P
x3 =
Yanıt B dir.
GY = P
GX = 2P
GY = P alınırsa GX = 2P olur.
Nihat Bilgin Yayıncılık©
T2
F1
T2
A
O
O
F2
P
P
G
G = 10 P
F3
Türdeş çubuğun ağırlığını bulmak için O noktasına
göre tork alınır.
1
P·2+P·3=G·
2
T2 ip gerilmesini bulmak için Oʹ noktasına göre
tork alınır.
10 · P ·
1
+ P · 1 = T2 · 3
2
T2 = 2P olur.
Yanıt C dir.
F1 kuvvetinin yatay bileşenine F dersek, kuvvetlerin A noktasına göre
τ1 , τ2 , τ3 torkları;
τ1 = F · 2
τ2 = F · 1
τ3 = F · 2
olarak bulunur. Buna göre,
τ1 = τ3 > τ2 olur.
Yanıt C dir.
14
Ünite 1
Kuvvet ve Hareket
9.
11.
F
O
M
6F
m = 4 kg
2F
37˚
3F
F
I
O
II
F
O
4 kg = 4000 gram
F
III
5 L = 5000 cm3
τ1 = F · 2 – 6F · sin37°
Musluk açıldıktan t dakika sonra dengenin bozulmaya başladığını varsayalım.
τ1 = 2F – 3,6F
τ1 = –1,6 F
4000 · 4 = 5000 · 1 · t
τ2 = 2F · 2 – 3F · 1
τ2 = F
τ3 = 3 · F + 2 · F
16
dakika
5
Buna göre, musluk açıldıktan sonra 3-4 dakika
arasında denge bozulmaya başlar.
τ3 = 5F
Buna göre,
τ3 > τ1 > τ2 olur.
30˚
T3
Nihat Bilgin Yayıncılık©
Yanıt C dir.
Yanıt C dir.
10.
t=
T2
a
T1
P
Şekildeki verilen düzeneğin yatay dengede olması
için;
T3 cos30° = T1
3
T3 ·
= T1
2
olmalıdır. Bu nedenle;
12.
T3
a
a
T3 > T1 olur.
P ağırlığının asıldığı noktaya göre tork alınırsa;
T3 · sin30° · 2 = T2 · 1
T2
T1
P
P
Her durumda ipteki gerilme kuvvetinin dönme noktasına uzaklığı, ağırlık merkezinin dönme noktasına
uzaklığının 2 katı olduğu için;
T3 = T2
olur. Buna göre ip gerilme kuvvetleri arasında;
T2 = T3 > T1 büyüklük ilişkisi vardır.
Yanıt D dir.
P
T1 = T2 = T3 =
P
olur.
2
Yanıt B dir.
TORK VE DENGE
13.
16.
T1
T2
P
T1
yatay
K
B
A
L
K
15
L
X
Y
20 N
T2
P ağırlıklı cisim hareket ederken P ağırlığının ve T2
kuvvetinin B noktasına göre döndürme etkileri eşit
olacaktır. Cisim ok yönünde giderken döndürme etkisi artacağından T2 nin de döndürme etkisi artacak yani T2 artacaktır.
20 N
40 N
Çubukların ağırlıklarının bileşkesi T2 nin uygulama
noktasında olduğu için T2 = 40 N ve T1 = 0 olur.
Yanıt A dır.
Sistem dengede olduğuna göre;
T1 = P + T2
dir. Cisim ok yönünde giderken P değişmeyip T2
arttığı için T1 de artmalıdır.
Yanıt D dir.
14.
T1
T2
15G
Çubuğun ağırlığı 15G olsun. İlk durumda T2 = 5G
ve T1 = 10G olur. Ayrıca çubuğun ağırlık merkezinin K nın bir birim sağında olduğunu söyleyebiliriz.
İkinci ip L noktasına kaydırıldığında, çubuğun ağırlık merkezi birinci ipten 1 birim, ikinci ipten 4 birim
uzakta olur. Bu durumda T2 = 3G ve T1 = 12 G
olur.
Buna göre T1 artarken, T2 azalır.
Nihat Bilgin Yayıncılık©
L
K
17.
Yanıt E dir.
F1 = F
O
F
15.Dengede olan 2P ağır-
lıklı çubuğa uygulanan
kuvvetlerin Y noktasına
göre torku alınırsa;
2P · 2 + P · 3 = T · 4 + T · 3
7P = 7T
F2 = F
2F
F3
T
T
X
τ = F · 1 alalım. F3 kuvvetini yatay ve düşey bile-
Y
şenlerine ayırıp, kuvvetlerin O noktasına göre bileşke torkunu alırsak;
P
2P
T = P olur.
Yanıt C dir.
F · 1 + F · 1 – 2F · 1 + F · 1 = F = τ olur.
Yanıt A dır.
16
Ünite 1
Kuvvet ve Hareket
18.
20.
L
K
T2
T2
T3
T3
T1
L
Şekil I
T
T1 = 0
K
G
P
L
K
T ipine göre K çubuğu için tork alırsak;
T3
T2
Şekil II
T1
G
Şekil I de çubuğu sağa çeken bir kuvvet olmadığı için T1 = 0 dır. Türdeş çubuğun ağırlığı T2 ve
T3 gerilme kuvvetlerinin tam ortasında olduğu için
T2 = T3 tür.
İp, Şekil II deki gibi K dan L ye kaydırıldığı zaman
T2 = Tʹ3 · cosa olur. Yani T2 gerilme kuvveti değişmezken T3 gerilme kuvveti artar.
Ayrıca son durumda çubuğu sağa çeken kuvvet arttığı için T1 de artmalıdır.
Yanıt B dir.
T1 · 3 = P
P
3
T1 ipine göre K çubuğu için tork alırsak;
T·3=P·2
2
P
3
T3 ipine göre L çubuğu için tork alırsak;
Nihat Bilgin Yayıncılık©
T1 =
T=
2
P · 1 = T2 · 3
3
2
T2 = P bulunur.
9
Buna göre;
P
3
=
2
T2
P
9
T1
T1
T2
=
3
olur.
2
Yanıt D dir.
19.
T1 = T
X
Y
2P
T2 = T
Z
K
L
4P
Çubuğun LN kısmı kesilip XZ üzerine yapıştırılınca
oluşan yeni şeklin ağırlık merkezi YZ arasında ve
Z ye daha yakındır. İp gerilme kuvvetlerinin değişmemesi için ağırlık merkezi iplere eşit mesafede olmalıdır. Buna göre T2 ipi KL arasından asılmalıdır.
Yanıt A dır.
TORK VE DENGE
3.
Test 4 ün Çözümleri
I
II
T1
1. Düşey duvar sürtünmesiz olduğundan düşeyde
dengenin sağlanması için F1 kuvveti, kalas ve m
kütlesinin ağırlıkları toplamına eşit olmalıdır. Bu nedenle F1 değişmez.
Y
P
P
Sistem dengede olduğu için yukarı doğru kuvvetler
aşağı doğru kuvvetlere eşit olmalıdır.
F2
F
T1 + T2 = 2P
X ucuna bağlı ip I konumundan II konumuna getirildiğinde T1 ipi ağırlık merkezine yaklaştığı için T1
gerilmesi artar, T2 azalır.
m
K
T2
X
düşey
yatay
Yanıt B dir.
F1
m kütleli cisim yükseldikçe K noktasına göre torku
artar. Dengeyi sağlayan F2 kuvvetinin de K noktasına göre torku artmalıdır. Yani F2 artar.
Yanıt D dir.
Nihat Bilgin Yayıncılık©
17
4.
T2
T1
a
L
K
T3
P
Sistem dengede olduğuna göre, sağa doğru kuvvetler sola doğru kuvvetlere eşit olmalıdır. Buna
göre;
2. X ve Y çubukları için ayrı
ayrı K noktasına göre
tork alalım.
Gx · 1 = T · 2
Gy · 2 = 2T · 4
T
X
K
53°
T
Y
2T
2T
=
4T
Gy
Gx
1
=
2
Gy
T3 = T2 · cosa
ifadesinde T3 ve a bilindiğinden T2 bulunabilir.
K noktasına göre tork alınırsa;
P · 2 = T2 · sina · 7
ifadesinde T2 ve a bilindiği için P bulunabilir.
L noktasına göre tork alınırsa;
T1 · 2 = T2 sina · 5
ifadesinde T2 ve a bilindiği için T1 bulunabilir.
T
GX
Gx
GY
olur .
Yanıt B dir.
Yanıt A dır.
18
Ünite 1
Kuvvet ve Hareket
5.
8. Sistem dengede olduğu-
F
na göre K dönme noktasına göre bileşke tork sıfır
K
olmalıdır. Şekildeki kırmızı boyalı karelerin ağırlık
P
merkezi K noktasında olduğu için tork oluşturmazlar. Bu durumda F kuvveti
ve P ağırlığının K noktasına göre torkları eşit olmalıdır.
T
Y
X
P
2P
Y noktasına göre tork alınırsa;
T · 3 = 2P · 2 + P · 2
T = 2P bulunur.
Yanıt A dır.
F · 1,5 = P · 2
F=
4
P olur.
3
Yanıt B dir.
6. X tuğlası Y tuğlasının
üstüne konulursa ya da Y
tuğlasının üstüne iki tuğla
daha konulursa sistemin
ağırlık merkezi desteğin
düşey doğrultusunda olacağından, denge sağlanır.
X
Yanıt D dir.
Nihat Bilgin Yayıncılık©
Y
9.
T
T1
K
I
7.
N
P
T2
II
P
K
L
L
P1
N
P2
Şekildeki I pozisyonunda T gerilme kuvveti ve P
ağırlığının K noktasına göre torku sıfırdır. T1 gerilme kuvvetinin K noktasına göre torkundan dolayı
denge ok yönünde bozulur.
P3
K noktasına göre tork alırsak;
P1 · 6 = N · 5
6
N = P1
5
L noktasına göre tork alırsak;
N · 3 = P3 · 2
6
· P1 · 3 = P3 · 2
5
P3
9
olur.
=
5
P1
Yanıt B dir.
II pozisyonunda T2 gerilme kuvvetinin L noktasına
göre torkundan dolayı denge ok yönünde bozulur.
III pozisyonunda
T3 gerilme kuvvetinin M noktasına
göre
torkundan
dolayı denge ok
yönünde bozulur.
M
T3
P
III
Yanıt E dir.
TORK VE DENGE
10.
12.
T
37°
19
yatay
yatay
x1
T
x2
30°
O
53°
58 N
60°
37°
yatay
O
O
Şekildeki kuvvetlerin çubuğa dik bileşenlerini bularak O noktasına göre tork alalım.
Her durumda yayın
yatay
uyguladığı kuvvetin
O
dönme noktasına dik
60°
x3
uzaklığı,
ağırlığın
denge noktasına dik
uzaklığının 2 katıdır.
Bu durumda tork alındığında kuvvetler eşit olur.
Yaylar özdeş olduğundan uzama miktarları da eşit
olacaktır.
T · sin30° + T · sin37° · 4 = 58 · sin53° · 2
0,5T + 2,4T = 58 · 1,6
T = 32 N bulunur.
Yanıt B dir.
Nihat Bilgin Yayıncılık©
Yanıt C dir.
13.Denge durumunda yukarı doğru olan kuvvetler aşağı doğru olan kuvvetlere eşit olmalıdır.
11.
T1
T4
Şekil I için;
2T1 · sin30° = P
T1 = P
yatay
T2
T3
T5
P
Bütün sistemi aşağıya çeken dış kuvvet P ağırlığıdır. T5 gerilme kuvveti tek başına bu ağırlığı dengeliyor. Diğer kuvvetler T2 ile T3 ve T1 ile T4 ise
bu ağırlığı paylaşıyor. Buna göre T5 gerilme kuvveti en büyüktür.
Yanıt E dir.
Şekil II için;
2T2 = P
P
2
Şekil III için;
2T3 · sin30° = P
T1
30°
30°
Şekil I
T2
T2 =
T3 = P
Buna göre, T1 = T3 > T2 olur.
Şekil II
30°
30°
T3
Şekil III
Yanıt A dır.
20
Ünite 1
Kuvvet ve Hareket
14.
16.Öncelikle T2 gerilme kuvvetini bileşenlerine ayıralım.
T
2F
F
F
T2·cos37°
T1
yatay
37°
K
15 N
20 N
T2·sin37°
İpteki F gerilme kuvvetlerinin bileşkesi K noktasındadır.
Desteğe göre tork alınırsa;
15 · 1 = T2 · sin37 · 1
K noktasına göre tork alırsak;
T · 5 = 20 · 2
Yatay dengenin sağlanması için;
T1 = T2 · cos37°
T1 = 25 · 0,8
T1 = 20 N
T = 8 N olur.
Yanıt C dir.
T2
T2 = 25 N bulunur.
olur.
15.
O
O
3F
2F
2F
F1
Şekil I
2F
F2
Nihat Bilgin Yayıncılık©
Yanıt D dir.
Şekil II
Şekil I deki F 1 kuvvetini bileşenlerine ayırıp O
noktasına göre tork alalım.
τ1 = 2F · d + 2F · 2d
τ1 = 6Fd
Şekil II deki F 2 kuvvetini bileşenlerine ayırıp O
noktasına göre tork alalım.
17.
F1
F2
r =10 cm
6 cm
8 cm
P
τ2 = 3F · d + 2F · 2d
τ2 = 7Fd
F 3 kuvvetinin O noktasına göre torku da;
τ3 = 3F · 2d
τ3 = 6Fd
olur. Buna göre;
4 cm
Ayrı ayrı K noktasına göre tork alalım.
F1 · 20 = P · 8
F1 = P · 0,4
F2 · 16 = P · 8
τ2 > τ1 = τ3 olur.
Yanıt B dir.
F2 = P · 0,5
Buna göre;
F1
F2
=
4
olur.
5
Yanıt D dir.
TORK VE DENGE
18.
20.
T1
F2
Z
21
2 birim
2
45°
Y
X
O
37°
O
2P
P
F1
Cisim Z noktasındayken O noktasına göre tork
alalım.
2P · 2 + P · 3 = 4T1
F3
Şekildeki F 1 , F 2 , F 3 kuvvetlerinin O noktasına
göre torkları;
7P = 4T1 ............................. (1)
Cisim X noktasındayken
alalım.
O noktasına göre tork
2P · 2 + P · 1 = 4T2
1 birim
5P = 4T2 ............................ (2)
τ1 = F1 · 1
τ2 = F2 ·
τ3 = F3 · 1
(1) ve (2) denklemleri taraf tarafa oranlanırsa;
T1
T2
=
7
olur.
5
Yanıt D dir.
Nihat Bilgin Yayıncılık©
1 birim
45°
45°
2
2
2
2
2
1
1
F1 ·
= F2 ·
= F3 · 2
2
2
bulunur. Buna göre, F1 = F3 > F2 olur.
Yanıt B dir.
21.
T1
T2
X
yatay
K
B
A
P
4P
yatay
L
19.Şekildeki gibi F 1 kuv-
vetini bileşenlerine ayıralım. Şimdi de yönlerine dikkat ederek O noktasına
göre tork alalım.
F3
F2
P
O
F
Şekildeki A noktasına göre tork alalım.
2F
R x = F1d1 + F2d2 – F3d3
R x = Fd + 2F · 2d + Fd –Fd
R x = 5Fd
F 2 nin O noktasına göre torku
R x = 5 x olur.
F1
x ise;
T1 · 3 = P · 2 + 4P · 1
T1 = 2P
B noktasına göre tork alalım.
T2 · 3 = P · 1 + 4P · 2
T2 = 3P
Buna göre;
T1
Yanıt C dir.
T2
=
2
3
olur.
Yanıt A dır.
22
Ünite 1
Kuvvet ve Hareket
4.
Test 5 in Çözümleri
F
O
r
Z
1. Kuvvetlerin hepsi aynı
noktaya etki ediyor. Dik
olarak etki eden F3 kuvvetinin K noktasına göre
döndürme momenti en
büyüktür.
L
K
2r
F
X
F3
Y
F
Moment = Kuvvet x Dik uzaklık
Yanıt C dir.
İki kuvvetin bileşkesi aralarındaki açı küçüldükçe
artar. C seçeneğinde ipler arasındaki açı en küçük
olduğundan bu sistem en çok yük kaldırabilir.
Yanıt C dir.
bağıntısını kullanarak her bir kuvvetin O noktasına
göre momentlerini (torklarını) bulalım.
MX = F · r
MY = F · 2r
MZ = F · r
Buna göre, momentler arasındaki ilişki;
MX = MZ < MY olur.
Yanıt C dir.
Nihat Bilgin Yayıncılık©
2. En çok yük kaldırılabilmesi için ip gerilme kuvvetlerinin bileşkesi en büyük olmalıdır.
5.
O
A
K
L
yatay
P
Oyuncak araba K-L arasındayken denge A noktası etrafında bozulur. Bu nedenle oyuncak arabanın
K ve L noktasında bulunduğu durumlar için A
noktasına göre tork alalım. Arabanın ağırlığı Pʹ olarak verilmiştir. Araba K da iken henüz denge bozulmamıştır. Bu yüzden;
3.
K
P
L
M
N
O
P · 1 = Pʹ · 1
P > Pʹ olur. Yani oyuncak arabanın ağırlığı P den
küçüktür.
Araba L ye gelmeden denge bozulmuştur. Bu nedenle,
P · 1 < Pʹ · 2
P
P
< Pʹ olur. Yani oyuncak arabanın ağırlığı
2
2
den büyüktür.
R
P
2P
2P
Önce P ağırlıklarının bileşkesi bulunur ve 2P olarak
şekildeki gibi yerleştirilir. Son durumda 2P yüklerinin bileşkesi MN arası olur.
Yanıt C dir.
Yanıt B dir.
TORK VE DENGE
6.
8.
3f
L
K
(–)
TK
f
O
r
r
53° 37°
127°
10 N
2f
Üç kuvvetin kesiştiği nokta için Lami teoremini uygulayarak tellerdeki gerilme kuvvetlerini bulabiliriz.
Döndürme yönlerine dikkat ederek kuvvetlerin O
noktasına göre torklarını alıp toplayalım.
R x = f · r + 2f · 3r – 3f · 2r
R x = f · r olur.
TL
O 143°
r
(+)
TK
sin 143 °
TK
sin 37 °
=
=
TL
sin 127 °
TL
sin 53 °
=
10
sin 90 °
=
10
1
Bileşke tork pozitif çıktığı için levha (+) yönde döner.
Buradan TK = 6 N ve TL = 8 N bulunur.
Yanıt B dir.
Halkalar ancak 7 N luk kuvvete dayanıklı olduğu
için önce L halkası kopar. L halkası koptuktan sonra
K halkasına düşen yük artar. Bu yüzden sonra da K
halkası kopar.
Nihat Bilgin Yayıncılık©
23
Yanıt D dir.
9. Kalasa uygulanan kuvvetler şekilde gösterilmiştir.
7.
F=1N
F
G
P = 10 N
Desteğe göre tork alınırsa, el kantarının gösterdiği
F değeri;
F · 3, = P · 2,
F=
2
P olur.
3
Desteğe göre tork alırsak;
F·4+G·2=P·1
1 · 4 + G · 2 = 10 · 1
Yanıt B dir.
G = 3 N bulunur.
Yanıt E dir.
24
Ünite 1
Kuvvet ve Hareket
10.
12.
( II )
mg
––
2
mg
––
2
(I)
F1x
yatay
F2
O
O
53°
mg
53°
Serbest bırakıldığı anda çubuğa şekildeki kuvvetler
döndürme etkisi uygular. Bu kuvvetlerin O noktasına göre döndürme etkileri eşit ve zıt yönlüdür. Bu
nedenle çubuk bırakıldığı gibi dengede kalır.
F1 = 12 N
37°
yatay
Sistem dengede olduğuna göre;
Yanıt C dir.
F2 = F1x olmalıdır.
F2 = F1 · cos53°
F2 = 12 · 0,6
F2 = 7,2 N
Nihat Bilgin Yayıncılık©
Yanıt D dir.
11.
M
L
K
P
Şekil I
Alev K noktasına geldiğinde, destek noktasına göre
sağ tarafın torku sol taraftan daha fazladır.
Alev L noktasına geldiğinde, destek noktasına göre
sol tarafın torku sağ taraftan daha fazladır ve kalas
sol tarafa döner.
13.
K
M
L
T
K
çubuk
P
G
P = 16 N
6G
Şekil II
Buna göre alev K-L arasında bir noktada iken kalas
dengeye gelir.
K dönme noktasına göre tork alınırsa;
Yanıt B dir.
16 · 5 = T · 8
T = 10 N bulunur.
Yanıt C dir.
TORK VE DENGE
14.
16.
F
O çubuk
L M
2F
yatay
K
M
25
d
N
(+)
L
G
F
Şekil I
destek
d
O
K
L
M
N
F
x
(–)
d
yatay
O
6–x
F
K
G = 3F
Şekil II
Döndürme yönlerine dikkat ederek kuvvetlerin O
noktasına göre torklarını alarak toplayalım.
destek
Şekil I de desteğe göre tork alınırsa;
G·2=F·6
G = 3F
R x = –2Fd
Bileşke tork negatif çıktığı için çubuk (–) yönde döner.
bulunur. Şekil II de desteği O noktasının x kadar
sağına koyalım ve desteğe göre tork alalım.
G · x = F · (6 – x)
3F · x = F · (6 – x)
R x = F · d + F · d – 2F · 2d
x = 1,5 birim olur.
Yani destek K ile L nin orta noktasına konmalıdır.
Yanıt B dir.
Yanıt B dir.
Nihat Bilgin Yayıncılık©
17.
15.
d
d
d
K
F3
d
F
F2
d
düşey
3P
F1
basamak
P
K noktasına göre tork alınırsa;
F 1 ve F 3 kuvvetlerinin doğrultusu dönme noktasından geçtiğine göre döndürme etkileri yoktur.
Yalnız F2 kuvveti tekeri basamağa çıkarabilir.
Yanıt B dir.
3
5
d+P· d
2
2
F = 7P olur.
F · d = 3P ·
Yanıt D dir.
26
Ünite 1
18.
Kuvvet ve Hareket
20.
düşey
K
yatay
K
L
M
N
yatay
A
a
X
a
a 2
45°
F2
F3
GX · 2 = GY · 4 ................ (1)
X cismi L noktasına kaydırıldığında yukarıdaki eşitliğin sol tarafı yarıya iner. Bu eşitliğin sağ tarafının
da yarıya inmesi için Y cisminin N noktasına kaydırılması gerekir. I. öncül doğrudur.
Y cisminin kütlesini yarıya indirmek de (1) eşitliğinin
sağ tarafını yarıya indirir. II. öncül de doğrudur.
Askı noktasının M ya da N noktasına getirilmesi
dengenin sola doğru kaymasını sağlar. III. ve IV.
öncüller yanlıştır.
F 1 , F 2 , F 3 kuvvetlerinin her biri tek başına cismi
dengede tutabiliyorsa kuvvetlerin K noktasına göre
torkları birbirine eşittir.
τ1 = τ2 = τ3
F1 · a = F2 · a 2 = F3 · a
F1 =
GY
Y
A noktasına göre tork alarak X ve Y cisimlerinin kütleleri arasındaki ilişkiyi bulabilirz.
F1
GX
2 F2 = F3
Bu durumda, F2 < F1 = F3 olur.
Yanıt A dır.
Nihat Bilgin Yayıncılık©
Yanıt C dir.
21.
F1
F2
K
P
19.
K
L
M N
yatay
yatay
P
P
P
P
2P
3P
Özdeş cisimlerin herbirinin ağırlığı P olsun. Sistemi
sola döndürmeye çalışan; P · 1 + P · 2 + P · 3 = 6P
döndürme etkisi vardır. Sağa doğru döndürmeye
çalışan 3P · 1 = 3P döndürme etkisi vardır. Çubuğun yatay dengede durabilmesi için sağa doğru 3P
lik daha döndürme etkisi gereklidir. Bu nedenle K
ve L noktalarına birer tane daha cisim asılmalıdır.
Yanıt A dır.
Türdeş ve özdeş tuğlaların ağırlğına P diyelim. Tuğlaların ortak ağırlık merkezi şekildeki gibi K noktasındadır.
F1 ve F2 kuvvetlerinin K noktasına göre torkunu
alırsak;
F1 ·
3
5
= F2 ·
2
2
F1
5
olur.
=
F2
3
Yanıt E dir.
TORK VE DENGE
22.
24.
T
27
yatay
K
yatay
Fk
P=2N
X
Y
Z
M
L
23 N
Bir cisim dengede ise, cisim üzerine etki eden kuvvetlerin vektörel toplamı sıfırdır. Başka bir ifadeyle,
sağa doğru kuvvetler sola doğru kuvvetlere, aşağı
doğru kuvvetler yukarı doğru kuvvetlere eşittir.
Çubuk üzerine etki eden bütün kuvvetler şekildeki
gibi gösterilir. Sistem dengede olduğuna göre kuvvetlerin bir yöndeki döndürme etkisi aksi yöndeki
döndürme etkisine eşittir.
M noktasına göre tork alırsak;
T · 3 = 2 · 2 + 23 · 1
Bu durumda, I. öncül yanlış, II ve III. öncüller doğrudur.
Yanıt E dir.
T = 9 N bulunur.
Nihat Bilgin Yayıncılık©
Yanıt C dir.
25.Şekil I de O noktasına
göre tork alınırsa;
K
L
yatay
mX · 1 = mY · 2
mX = 2 mY
Y
X
eşitliği bulunur.
Şekil I
FX
FY
K
23.
O
O
L
yatay
F1
F5
X
Y
su
O
F2
F3
Doğrultusu dönme noktasından geçen kuvvet döndürme etkisi oluşturmaz.
Şekil II
F4
Şekildeki F2 kuvvetinin doğrultusu O dönme noktasından geçmektedir. Bu yüzden F2 kuvvetini kaldırmak levhanın dengesini bozmaz.
Yanıt B dir.
Şekil II de yatay denge bozulmadığına göre
FX = 2FY olmalıdır.Buna göre;
VX · dsu · g = 2 · VY · dsu · g
VX = 2VY
olur. Bu durumda cisimlerin kütleleri oranı hacimleri
oranına eşittir. Bu nedenle özkütleleri de eşit olmalıdır.
Yanıt A dır.
28
Ünite 1
Kuvvet ve Hareket
26.
29.
K ipi
yatay
X
yatay
O
Z
A
Y
L ipi
Bilye ok yönünde hareket ederken A noktasına göre
döndürme etkisi artar. Bu döndürme etkisini dengelemek için L ipindeki gerilme kuvveti de artacaktır.
Düşey denge şartı yazılırsa;
TK = TL + Gbilye + Gçubuk
Bu ifadeye göre, TL artarsa, TK da artar.
mX , mY , mZ kütleli X, Y, Z cisimleri ile dengede
olan çubuğun destek noktasına göre torku alınırsa;
2mX + 2mY = 3mZ
eşitliği yazılır. Y cisminin kütlesinin sıfır olduğunu
varsayalım.
Yanıt B dir.
mX
3
mZ = 2
mX
3
olarak bulunur. Buna göre m oranı kesinlikle
2
Z
den daha küçük olmalıdır.
Yanıt A dır.
27.Özdeş her bir cismin ağırlığına G diyelim.
K
L
M
N
P
R
G
2G
4G
Bu ağırlıkların O noktasına göre torkunu alırsak,
7G < 8G olduğu görülür.
Dengenin sağlanması için sol tarafta G kadar artış
gerekir. M deki cismi L ye kaydırma bu artışı gerçekleştirir.
Nihat Bilgin Yayıncılık©
O
30.Cisimlerin L noktasına göre torku alınırsa, Y cisminin kütlesi;
3m = 2mY
mY =
3
m olarak bulunur.
2
Yanıt B dir.
x
K
L
M
N
P
R
yatay
28.
ip
3m X
yatay
O
X
Y
mX · 2 = mY + mZ · 2
eşitliği yazılır. Buna göre X in kütlesi Z ninkinden
kesinlikle büyük olmalıdır. Ancak X ile Y ve Y ile Z
nin kütleleri karşılaştırılamaz.
Yanıt B dir.
3m Y
2
Z 2m
Çubuğun asılma noktası M ye kaydırıldığında, yatay dengenin bozulmaması için 2m kütleli Z cisminin M noktasından x kadar uzağa asıldığını varsayarsak;
3m · 2 =
9
birim bulunur. Buna göre Z cismi M noktası4
9
nın
birim uzağında P ile R nin arasına asılmalı4
dır.
Z
Dengede olan düzenekte O noktasına göre tork alınırsa;
ip
3m
· 1 + x · 2m
2
x=
Yanıt D dir.
TORK VE DENGE
31.
K
L
M
29
33.
N
yatay
PL
duvar
mg
L
mg
K
2mg
M
Çubuğun kütlesi ile m kütleli cismin kütle merkezi
şekildeki N noktasındadır.
K
L
M
yer
N
2mg
PL
P
Sistem dengede olduğuna göre P ve PL kuvvetlerinin M noktasına göre döndürme etkileri eşit olmalıdır.
yatay
2mg
4mg
Böylece N noktasındaki 2mg ile 2m kütleli cismin
ağırlığının bileşkesi ikisinin tam ortasında L noktasında olur.
37° yatay
Şekildeki M noktasına göre tork alırsak;
P·
1
= PL · sin37° · 1
2
5
PL = P bulunur.
6
Yanıt E dir.
Çubuk bileşke kuvvetin olduğu L noktasından asılırsa dengede kalır.
Nihat Bilgin Yayıncılık©
Yanıt C dir.
34.
tavan
M
T
T
yatay
A
32.
F
mKg
K
su
P
ip
Çubuğa etki eden bütün kuvvetleri şekildeki gibi
gösterebiliriz.
T
İplerdeki T gerilme kuvvetlerinin bileşkesi A noktasındadır. K ve L cisimlerinin A noktasına göre döndürme etkileri eşit olacaktır.
Bu nedenle A noktasına göre tork alalım.
mK · g · 0,5 = mL · g · 2,5
mK
m L = 5 bulunur.
Önce şekildeki gibi çubuğa etki eden bütün kuvvetleri gösterelim.
Şimdi de K noktasına göre tork alalım.
F·
mLg
3
=P·2
2
4
F = P bulunur.
3
Yanıt D dir.
Yanıt B dir.
30
Ünite 1
Kuvvet ve Hareket
35.
37.
v
2v
NX
1
NY
2
X
Y
yatay
1. Yol
Şekildeki sistemin dengede olabilmesi için
mK = 2mL olmalıdır.
İşçilerin kütleleri eşit olup süratleri farklıdır. 2 numaralı işçinin sürati 2v olduğundan Y desteğine daha
hızlı bir şekilde yaklaşır. Bu durumda Y desteğinin
NY tepki kuvveti artar, X inki azalır.
2. Yol
İşçilerin kütleleri eşit olup süratleri farklıdır. 2 numaralı çocuğun sürati 2v olduğundan çocukların ortak
kütle merkezi Y desteğine doğru hareket eder. Bu
durumda Y desteğinin NY tepki kuvveti artar, X inki
azalır.
x tane L
K ve L nin yerleri şekildeki gibi değiştirilirse, denge
durumu aşağıdaki gibi yazılabilir.
x · mL · g · 1 = mK · g · 2
x · mL = 2mL · 2
x=4
Yanıt B dir.
Nihat Bilgin Yayıncılık©
Bu durumda L nin altına 3 cisim daha asılmalıdır.
Yanıt C dir.
36.
duvar
K
38. L
ipi
d
T2
K
2d
T1
37°
T2
T1
O
O
P
P
O
Şekildeki OOʹ kalasına etki eden T, TL kuvvetlerinin O noktasına göre döndürme etkileri birbirine eşit
olmalıdır. Buradan;
M
L
TL
L ipi
T
yer
(yatay)
M
Şekil I
Şekil I de T2 nin karşısındaki açı dar açıdır. Bu nedenle T2 , P ve T1 den büyüktür. T1 ve P karşısındaki açılar eşit olduğu için T1 = P dir.
Şekil II de P nin karşısındaki açı dar açı olduğu için
P en büyük olmalıdır. Bunun için hem T1 , hem de
T2 azalmalıdır.
TL · 2d = T · cos37° · 3d
TL · 2 = T ·
TL =
4
·3
5
6
T bulunur.
5
Yanıt A dır.
Şekil II
Yanıt A dır.