ŞİİRLERİMİZ

Aylin Karaahmet
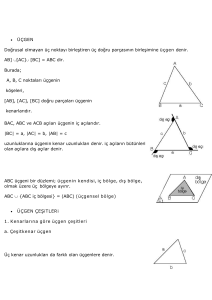
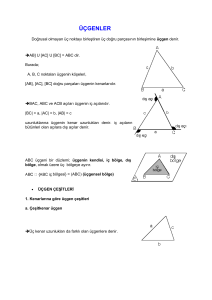
A, B ve C doğrusal olmayan üç nokta olmak
üzere [AB], [BC] ve [CA]’nın birleşimine ÜÇGEN
denir.
A
Köşe
Z
X
B
Y
1. A, B ve C noktaları
üçgenin köşeleridir.
2. [AB], [BC] ve [AC]
üçgenin kenarlarıdır.
3. |BC|= a
|AC|= b
|AB|= c üçgenin kenar
uzunluklarıdır.
C 4. A, B ve C
köşeleri üçgenin iç
açılarıdır.
Matematikte karşımıza en çok çıkan
geometrik şekil üçgendir. Çokgenler içinde
kenar sayısı en az olan üçgenler. Diğer
çokgenlerle ilgili özellikleri de ortaya çıkarır.
Bir üçgeni çizebilmek için bu üçgene ait bazı
elemanların ölçülerini bilmemiz gerekir:
1. üçgenin bütün kenar uzunlukları veya
2. üçgenin iki kenar uzunluğu ve bu kenarlar
arasındaki açı veya
3. üçgenin iki açısı ve bir kenar uzunluğu
1. Önce [KL]’i çizelim. K
L
2. K noktasını merkez alarak açı ölçerle 70°yi
LKM çizelim. ΙKMΙ = 4 cm olsun.
M
L ve M noktalarınıbir
doğru parçası ile birleştirelim.
70°
K
5 Cm
L
Kenar uzunlukları 6 cm ve 8 cm olan, arasındaki
açısı 45° olan üçgen çiziniz.
1) Yükseklik: Üçgenin bir köşesinden karşı
kenarına veya karşı kenarının uzantısına çizilen dik
doğru parçasıdır. “h” ile gösterilir.
h
h
1) Bir ABC üçgeninde üç kenara ait yükseklikler
A
ha
c
ha
a kenarına ait
yükseklik
b
hc
Diklik
Merkezi
hb
B
C
a
2) Üçgen DİK AÇILI bir üçgense; DİK KENARLARIN
İKİSİDE üçgenin yüksekliğidir.
a kenarına ait
c kenarı
A
A
a kenarı
b
c
B
a
ha
C
B
yükseklik
c kenarına ait
yükseklik
b
hc
C
3) Geniş açılı bir üçgende yükseklikler
çizildiğinde iki yüksekliğin üçgenin dışında
diğer yüksekliğin içinde olduğu görülür.
A
7 br
B
5 br
C
ABC üçgeninde s(C) < s(A)
ise |BC|’nin en küçük tam
sayı değeri için yükseklikler
nasıl sıralanır?
|AB|-|AC|<|BC|<|AB|+|AC|
7-5<|BC|<7+5
2<|BC|<12 Açılara göre
|BC|<7
|BC|=8 br.
a=8 br, b=5 br, c=7 br
ha<hc<hb’dir.
1-) Bir ABC ninde a,b ve c kenar uzunlukları
olmak üzere a < b < c ise ha > hb > hc dir.
Terside doğrudur.
EN UZUN KENARA AİT YÜKSEKLİK EN KISADIR.
2-) Bir ABC ninde s(A) > s(B) > s(C) ise
ha < hb < hc dir.
AÇILARLA YÜKSEKLİKLER DE TERS ORANTILIDIR.
Bir ABC ninde s(A) = 63° ve s(B) = 57° ise
yükseklikler arasındaki ilişki nasıldır?
s(C)=180°-(57°+63°)=60°
|AD|<|CF|<|BE|
A
c
b
E
F
B
C
D
s(A)>s(C)>s(B)
ha<hc<hb
Üçgenin bir köşesinden karşı kenarı iki eş parçaya
ayıracak şekilde çizilen doğru parçasıdır. “V” ile
gösterilir.
V
//
//
NOT: Bir üçgende
üç kenarortay bir
noktada kesişir.
Üçgenin ağırlık merkezi
A
Va
Vb
Vc
Va
Vc
Vb
B
//
//
C
a kenarına ait kenarortay
b kenarına ait kenarortay
c kenarına ait kenarortay
A
ABC’nde |AD|=12 br.
olduğuna göre |AG| kaç
br. dir?
E
G
B
//
D
//
C
|AG|=2|GD|
|GD|= k ise |AG|=2k
|AD|=|AG|+|GD|
= 2k + k =3k
12=3k
k=4
|AG|= 2k = 2.4 = 8br. dir
E
ABC ninde
I EG I = 2x – 2 br
I GC I = 3x+1 br olduğuna göre I
EC I = ? Br dir.
I GC I = 2 I EG I
3x+1 = 2.(2x-2)
3x+1 = 4x-4
5=x
I EG I = 2x-2
2.5 – 2= 8 br
I GC I = 3x+1
3.5 + 1= 16 br
I EC I = 8 + 16 = 24 br
Üçgenin bir köşesindeki açıyı iki eş parçaya
ayıran doğru parçasıdır. “n” ile gösterilir.
n
İç açıortay
Dış açıortay
A
na
nb
na
nc
nb
B
C
a kenarına ait açıortay
b kenarına ait açıortay
I DA I = I BD I s ( ABD ) = 80° ( ikizkenar)
Bir dış açı kendisine komşu olmayan iki iç açının
ölçüsünün toplamına eşittir.
s ( D ) = 80° + 80° = 160°
s ( B ) = 10° ve s ( C ) = 10° (ikizkenar üçgen)
[CE]
[AD]
I AE I = I ED I
I AB I = I CD I
s ( BAC ) = 68°
s (CAD ) = ?
[CE] , AD nin kenar ortayı olup
ACD ikiz kenar olur. Öyle ise
I AC I = I CD I dir.
s (ABC) = s(ACB)
= (180° - 68° ) / 2
= 56°
s (ACD) = 180° - 56° = 124°
s (CAD) = ( 180° - 124° ) / 2
= 28°
TANIM : Bir kenarı dik olarak iki eş parçaya böler.
NOT : Bir üçgende kenar orta dikmelerin kesim
noktası dış teğet çemberin merkezidir.
Üçgenlerin kenarlarıyla açıları arasında
bazı bağıntılar bulunmaktadır. Kenar
uzunlukları her istenen değeri alamaz.
1.) Bir üçgende büyük açı karşısında büyük
kenar, küçük açı karşısında küçük kenar
vardır. Yada büyük kenar karşısında büyük
açı, küçük kenar karşısında küçük açı vardır.
A
a>b>c
s(A)>s(B)>s(C)
70°
b
c
50°
60°
B
a
C
2.) Bir üçgende eş uzunluklar karşısında eş
açılar ya da eş açılar karşısında eş uzunluklar
vardır.
A
s(B)=s(C)>s(A)
b=c>a dır.
40°
b
c
70°
70°
B
a
C
Bir üçgende açılardan biri dik açı ya da geniş
açı ise, o açı karşısındaki kenar en büyüktür.
A
A
b
b
c
c
120°
B
B
a
C
a
C
b>d>e
a>b>c
En uzun kenar [BC] dir.
Şekildeki ABC üçgeninde
I AB I = 4 cm
I AC I = 9 cm
I BD I = 12 cm
[BC]
[CD] olduğuna göre
[BC] kenarının alabileceği
tam sayı değerleri toplamı
kaçtır?
ABC üçgeni için I BC I nin alabileceği değerler:
I 9-4 I < I BC I < I 9+4 I
5 < I BC I < 13
Ayrıca s (BCD) = 90° [BD] → BCD üçgeni için
en uzun kenardır.
I BC I < 12
Buradan 5 < I BC I < 12 olur.
Toplam= 6+7+8+9+10+11 = 51 dir.
Şekilde s ( A ) > s ( B )
I AC I = 18 cm
I BC I = 2x + 8 cm
I AB I = x + 4 cm
x’ in alabileceği tamsayı
değerleri ?
x – 6 < 10 →
10 < 3x – 2 →
x < 16
12 < 3x
→ 4<x
s(B)> s(C)
2x – 4 > 10
2x > 14
→ x>7
7 < x < 16
C = { 8,9,10,11,12,13,14,15 }