İstatistik ve Olasılık

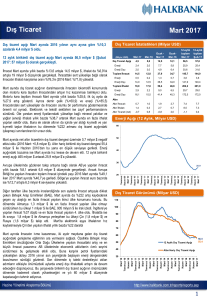
Açıklayıcı İstatistik
İstatistik ve Olasılık
Ders 2: Açıklayıcı İstatistik
Prof. Dr. İrfan KAYMAZ
Atatürk Üniversitesi
Tanım
Açıklayıcı İstatistik
İnceleme sonucu elde edilen ham verilerin istatistiksel yöntemler kullanılarak
özetlenmesi açıklayıcı istatistiği konusudur.
Açıklayıcı istatistikte kullanılan yöntemler:
Frekans Tabloları
Şekiller ve Grafikler
Histogram ve Frekans Poliganları
Sütun ve Pasta Grafikleri
Atatürk Üniversitesi
Frekans Tabloları
Açıklayıcı İstatistik
Kullanılan en yaygın yöntemlerden biridir.
Örnek Frekans Tablosu
Atatürk Üniversitesi
Açıklayıcı İstatistik
Frekans Tabloları
Verileri frekans
özetlenebilir:
tabloları
yardımıyla
sınıflandırmanın
yararları
şöyle
İlgili değişkenin dağılımı hakkında bilgi alınabilir.
Verilerin hangi değerler etrafında gruplandığı görülebilir.
Ortalama, standart sapma ve varyans gibi değerler daha kolay
hesaplanabilir.
Bu yararlarına karşın verilerin sınıflandırılması sırasında (özellikle sınıf
aralıklarının geniş tutulması halinde) bilgi ve hassasiyet kaybı olmaktadır.
Çünkü, herhangi bir sınıfın aralığı içine düşen farklı değerler sadece o aralığın
orta değeri ile temsil edilirler.
Atatürk Üniversitesi
Frekans Tabloları
Açıklayıcı İstatistik
Frekans tablolarının düzenlenmesinde aşağıdaki sıra izlenir:
1.Sınıf sayısı belirlenir (5 ila 20 arasında olur).
Sturgess kuralıSS=1+3.2*log(n)
2. Verilerin değişim genişliği bulunur (DG=enbüyük değer - enküçük değer)
3. Yaklaşık sınıf aralığı bulunur (SA=DG/sınıf sayısı)
4. Birinci sınıfın alt limiti veri grubundaki en küçük değeri içine alacak şekilde
belirlendikten sonra, hesaplanan sınıf aralığı bu değere eklenmek suretiyle
diğer sınıfların alt limitleri oluşturulur. Bir sınıfın üst limitini bulmak için bir
sonraki sınıfın alt limitinden belirli bir değer (veri grubunun özelliğine göre
yeteri kadar küçük bir değer) çıkarılır. Böylece sınıf aralarına değer düşmesi
önlendiği gibi, bir değerin iki ayrı sınıfa dahil edilmesi de engellenmiş olur.
5. Sonuncu sınıfın üst limiti veri grubundaki en büyük değeri içine alacak
şekilde belirlenir.
Atatürk Üniversitesi
Frekans Tabloları
Açıklayıcı İstatistik
Frekans tablolarının düzenlenmesinde aşağıdaki sıra izlenir:
6. Sınıf limitlerinin ortalamaları alınarak sınıf değerleri (sınıf ortalamaları)
belirlenir.
7. Veriler taranarak her sınıfa düşecek veri sayısı (frekans) belirlenir.
Frekans tablosundaki her bir sınıf için nispi (oransal) frekans, eklemeli frekans ve
eklemeli nispi(oransal) frekans değerleri hesaplanır.
Nispi Frekans: bir sınıfın frekansının (n) toplam veri sayısına (N) bölünüp, 100 ile
çarpılması ile elde edilir.
Eklemeli Frekans: Herhangi bir sınıfın frekansı ile o sınıftan önceki sınıfların
frekanslarının toplanması ile elde edilir.
Eklemeli Nispi Frekans: bir sınıfın eklemeli frekansının toplam veri sayısına (N)
bölünüp 100 ile çarpılmasıyla elde edilir.
Atatürk Üniversitesi
Açıklayıcı İstatistik
Frekans Tabloları
Örnek 1:
Bir dolum tesisinde doldurulmakta olan bakliyat paketlerinden rastgele
seçilen 40 paketin ağırlıkları kg olarak aşağıda verilmiştir.
2.3
1.6
3.2
4.3
3.6
4.1
3.1
3.6
3.1
3.2
3.6
3.2
2.8
4.2
4.4
4.5
3.7
3.4
1.8
3.5
3.1
3.1
3.8
3.4
3.8
4.7
3.1
4.7
3.2
3.9
3.3
3.9
2.8
2.6
3.0
3.4
3.3
4.2
3.6
2.7
Sınıf sayısını 7 alarak frekans tablosunu oluşturunuz.
Nispi (izafi) frekansları, birikimli ve birikimli nispi frekansları hesaplayınız.
Atatürk Üniversitesi
Frekans Tabloları
Açıklayıcı İstatistik
Örnek 1 ÇÖZÜM:
DG=4.7-1.6=3.1 
SA=3.1/7=0.440.5
Veriler dikkate alınarak alt ve üst limitleri belirlemede kullanılacak yeterince küçük
değer=0.1 olarak seçilebilir.
Sınıf alt limitleri  1.6-0.1=1.5 1.5+0.5=2.0 2.0+0.5=2.5 3.0 3.5 4.0 4.5
Sınıf üst limitleri  2.0-0.1=1.9 1.9+0.5=2.4 2.4+0.5=2.9 3.4 3.9 4.4 4.9
Sınıf sınırları  (2.0-1.9)/2=0.05 birinci sınıf için 1.5-0.05=1.45 ve 1.9+0.05=1.95
Nispi frekans  (2/40)*100=%5 (1/40)*100=%2.5 (4/40)*100=%10
Atatürk Üniversitesi
Frekans Tabloları
Açıklayıcı İstatistik
Örnek 1 ÇÖZÜM:
Frekans tablosunun tarama sütununa bakıldığında verilerin hangi değerler
etrafında yoğunlaştığı ve veri grubuna ait dağılımın şekli kabaca görülmektedir
Atatürk Üniversitesi
Açıklayıcı İstatistik
Şekiller ve Grafikler
Anlamlı bilgileri çıkarabilmek için şekillerin
ve grafiklerin çiziminde eksenlerin orantılı
olmasına ve gerekli açıklayıcı bilgileri
bulundurmasına dikkat edilmelidir. Verileri
şekil ve grafiklerle göstermenin yararları
aşağıdaki gibi özetlenebilir:
4
2
0
-2
-4
2
1
2
1
0
Anlaşılabilirlik artırılır.
Dikkat çekilecek hususlar belirtilir.
Dağılımın biçimi hakkında bilgi sağlanır.
Tahmin kolaylaşır
0
-1
-1
-2
-2
60
40
20
6
0
5
4
1
3
2
2
1
Atatürk Üniversitesi
Histogram ve Frekans Poligonları
Açıklayıcı İstatistik
X eksenine sınıf sınırları, Y eksenine frekans
değerleri yazılarak her bir sınıf için
oluşturulan
dikdörtgenlerin
meydana
getirdiği şekle histogram denir.
Her bir dikdörtgenin alanı ilgili sınıfın
frekansını ifade etmektedir. Örnek1’e göre
oluşturulan frekans tablosunun histogramı
yandaki gibi çizilebilir.
Şekildeki dikdörtgenlerin orta noktalarının birleştirilmesiyle frekans poligonu
elde edilir. Poligondaki kırık çizgilerin kaldırılmasıyla (bunun için gözlem
sayısının yeterince artırılması gerekir) verilerin dağılım biçimi kabaca
belirlenebilir.
Atatürk Üniversitesi
Histogram ve Frekans Poligonları
Açıklayıcı İstatistik
Dağılımın biçimine bakılarak veri grubu hakkında ilk basit değerlendirmeleri
yapmak mümkündür. Sözgelimi, dağılımın simetrik değil de herhangi bir yöne
çarpık olması;
Örneklemenin hatalı yapıldığı,
Ölçüm skalasının yanlış seçildiği,
Örnek büyüklüğünün yetersiz olduğu
anlamına gelebilir.
Ayrıca çizilen histogramın veya frekans poligonunun tepe değerinin birden
fazla olması;
İlgili anakütlenin homojen olmadığını ve
Örnek büyüklüğünün artırılması
gerektiğini gösterir. İncelenen verilere ilişkin dağılım her zaman normal
dağılım olmayabilir.
Atatürk Üniversitesi
Histogram ve Frekans Poligonları
Açıklayıcı İstatistik
Yukarıdaki frekans tablosunda verilen birikimli frekans değerleri Y eksenine,
sınıf üst (veya alt) sınırları X eksenine yazılır ve ilgili değerler grafiğe noktalar
halinde işlenip, bu noktalar birleştirilirse aşağıdaki birikimli frekans poligonu elde
edilir
Birikimli frekans poligonu yardımıyla belirli orandaki değerlerin hangi değerden
daha küçük veya hangi değerden daha büyük olduğu belirlenebilir
Atatürk Üniversitesi
Açıklayıcı İstatistik
Sütun ve Pasta Grafikleri
Miktarlar arasındaki ilişkiyi göstermek için X eksenine sınıf veya alt sınırlar,
Y eksenine mutlak veya nispi miktarlar yerleştirilerek çizilen grafiklerdir.
Örnek 2:
Kamu ve özel sektörleri tarafından yapılan şeker üretiminin yıllara göre dağılımı
aşağıdaki tabloda verilmiştir. Verilere ait sütun grafiğini çiziniz.
Yıllar
1967
1968
1969
1970
1975
Kamu
438301
411921
351619
315307
494000
Özel
224915
305700
235573
202703
312000
Toplam
663216
717621
587192
518010
806000
Atatürk Üniversitesi
Sütun Grafiği
Açıklayıcı İstatistik
Örnek 2 Çözüm:
Atatürk Üniversitesi
Pasta Grafiği
Açıklayıcı İstatistik
Bir bütünü meydana getiren parçaların ifade edilmesinde kullanılan
grafiklerden biri de bölünmüş daire (pasta) grafikleridir. Bu grafikleri çizerken
dairenin bütün alanı %100 kabul edilir. Merkezdeki 3.6 derecelik açı %1’e karşı
geldiğinden (360/100=3.6) parçaların kaçar derece açıyla gösterileceği
hesaplanır.
Örneğin yan tarafta çizilen ve bir
üniversitedeki
faaliyetlerin
dağılımını
gösteren bölünmüş daire grafiği şöyle
yorumlanabilir:
Bu
üniversitedeki
faaliyetlerin %65’i eğitim-öğretim, %20’si
araştırma, %15’ide yayın ve halk hizmeti
olarak verilmektedir
Atatürk Üniversitesi
Dersin Özeti
Açıklayıcı İstatistik
Araştırmalar sonucu elde edilen veri grupları belirli bir
şekilde sınıflandırılmadan veya uygun grafiklerle
gösterilmeden veri grubu hakkında ilk basit
değerlendirmeyi
yapmanın
mümkün
olmadığı
söylenebilir.
Atatürk Üniversitesi
Gelecek dersin konusu
Açıklayıcı İstatistik
Merkezi Eğilim ve Dağılma Ölçüleri….
Atatürk Üniversitesi