7. Sınıf 2. Ünite Kuvvet ve Hareket (Korumalı PDF).

Sarmal Yaylar
Kuvvet uygulandığında bazı cisimlerin şekillerinde
değişiklikler olduğunu, uygulanan kuvvet ortadan kalktığında
ise bu cisimlerin ilk şekillerine dönerler. Bu tür cisimlere,
esnek cisimler denir.
Örneğin, giydiğimiz bazı tişört ve çoraplar esnektir.
Onları, giyebilmek için gereriz. Çıkardığımızda ise bu giysiler,
ilk şekillerine döner. Oyun hamuru ve cam macunu gibi
maddeler esnek değildir. Onlara kuvvet uyguladığımızda
şekillerini değiştirebiliriz. Fakat uyguladığımız kuvvet ortadan
kalktığında bu maddeler eski hâllerine dönmezler.
2
Sarmal Yaylar
Yay gibi cisimler esnektir. Gererek ya da
sıkıştırarak onların şekillerini değiştirebiliriz.
Uyguladığımız kuvveti ortadan kaldırdığımızda ise
yay eski hâline döner.
3
Sarmal Yaylarda
Kuvvet – Uzama İlişkisi
Bir yaya kuvvet
uyguladığımızda yay,
kuvvetin büyüklüğüyle
orantılı olarak uzar ya
da sıkışır.
4
Sarmal Yaylar (Soru)
Kuvvet – uzama grafiği şekildeki gibi olan bir
yayı 12 cm uzatabilmek için uygulanması
gereken kuvvet kaç N’dur?
A) 25
B) 30
C) 60
D) 120
5
İŞ
Günlük hayatımızda zihinsel ve bedensel
faaliyetlerimizi anlatırken iş sözcüğünü kullanırız.
Fizikte ise iş, kuvvet ile hareket arasında bir
ilişkidir. İş, skaler bir büyüklüktür ve W ile
gösterilir.
Birimini formülden çıkaralım.
W(İş) = F (Newton) . X (Metre)
W (İş) = Newton.Metre olur.
Buna fizikte joule (J) denir.
6
İş – Kuvvet İlişkisi - 1
Buzdolabına kuvvet uygulayarak onun yerini
değiştirdiğimizde bir iş yapmış oluruz. Ancak aynı
dolaba kuvvet uyguladığımız hâlde onun yerini
değiştiremiyorsak yorulduğumuz hâlde bir iş yapmış
sayılmayız. Niçin?
Buna göre yandaki resimlerden hangisinde bir
iş yapıldığını söyleyebiliriz?
İş yapmış olabilmemiz için uyguladığımız
kuvvetin yönü ile cismin aynı yönde yer değiştirmiş
olması lazımdır. Buna göre kapı hareket ederken iş
yapmış oluruz. 2. durumda kapı kuvvet sonucu yer
değiştirme olmayınca iş yapmış olmayız.
7
İş – Kuvvet İlişkisi - 2
İş formülündeki kuvvet miktarı arttıkça
yapılan iş de artar. Yani, kuvvet ile iş doğru
orantılıdır.
Bu bilgi ile aşağıdaki resmi yorumlayalım.
Hangi durumda iş daha fazladır?
8
İş – Kuvvet İlişkisi - 3
İş formülümüzdeki kuvvet ile yol arasındaki ilişki de önemlidir. İş
yapılabilmesi için cisme uygulanan kuvvetin hareketle aynı
doğrultuda olması gerekir. Aksi takdir de fizikte ki anlamıyla bir işten
bahsedemeyiz. Bu durumu aşağıdaki resimlerle yorumlayalım.
A resminde kuvvet yukarı doğru iken hareket farklı yöne
doğrudur. Diğer 1 ve 2 numaralı resimlerde ise çocuk kitabı alıp yukarı
doğru kuvvet uygularken, kitabı da üst rafa koymaktadır Yani hareket
ve kuvvet yönü aynıdır.
Dolayısıyla, A resminde işten bahsedemezken; 12 numaralı resimlerde işten bahsedebiliriz.
9
İş – Enerji - Sürtünme
10
İş (Soru)
Sürtünmesiz yatay düzlemde durmakta olan cisim
şekildeki kuvvetlerin etkisiyle x kadar yol alıyor.
Buna göre, kuvvetlerin yaptığı toplam iş kaç F.x’tir?
A) 2
B) 3
C) 4
D) 6
11
Enerji
İş yapabilme yeteneğine enerji denir. İş yapabilmek için
enerji harcamak gerekir. Yaptığımız işin sonunda kendimizi
yorgun hissetmemizde enerji harcadığımızın belirtisidir.
İş birimleri ile enerji birimleri aynıdır. Yani “joule”dur.
Enerji skaler bir büyüklüktür.
Bazı enerji çeşitleri:
• Mekanik enerji
(Kinetik ve potansiyel enerjinin toplamıdır.)
• Elektrik enerjisi
• Nükleer enerji
• Kinetik enerji
• Potansiyel enerji
12
Kinetik Enerji
Cismin hareketinden (hızından) dolayı sahip
olduğu enerjiye kinetik enerji denir. Cismin
kütlesi (m) ve hızının karesi (v2) ile doğru
orantılıdır. Kinetik enerji Ek ile gösterilir.
13
Kinetik Enerji (Soru)
5 m/s hızla hareket eden 4 kg kütleli cismin
kinetik enerjisi kaç joule’dür?
A) 20
B) 40
C) 50
D) 100
14
Potansiyel Enerji
Potansiyel enerjiye durum enerjisi de denir.
Dalda duran elmanın, çatıda duran kiremitin,
gerilmiş ya da sıkışmış yayın potansiyel enerjisi
vardır.
Bu potansiyel enerji
iki kısımda incelenir:
1. Çekim Potansiyel
2. Esneklik Potansiyel
15
Çekim Potansiyel Enerjisi
Yerçekimi
kuvvetinin
cisimlerde meydana getirdiği
enerjidir.
Cisimlerin bulundukları
yükseklikten dolayı sahip
oldukları
depolanmış
enerjiye çekim potansiyel
enerjisi denir.
Potansiyel enerji Ep ile
gösterilir.
16
Esneklik Potansiyel Enerjisi
Gerilen ya da sıkıştırılan
yayda da enerji depolanır. Bu
enerji esneklik potansiyel
enerjisidir.
17
18
19
20
Enerjinin Korunumu
Bir cisme dışarıdan etki eden kuvvet yoksa
cismin mekanik enerjisi değişmez.
Günlük dilde enerjinin harcanması ve
tüketilmesi sıkça kullanılır. Aslında enerji yok
olmayıp başka bir enerjiye dönüşmektedir.
Yani, yukarıda duran elma potansiyel enerjiye
sahipken, aşağı düştüğünde potansiyel enerjisi
azalır, kinetik enerjisi artar.
21
Verim
Bir makine genelde ürettiğinden
daha fazla güç tüketir. İdeal bir
sistemde sisteme harcanan enerji,
elde edilen enerjiye eşittir.
Bir sistemin verimi sistemden
elde edilen enerjinin, sistemin
harcadığı enerjiye oranıdır.
22
BASİT MAKİNELER
Günlük hayatta bir işi daha kolay yapmak için tasarlanmış
aletlere basit makineler denir. Birden fazla basit makine
birleşerek birleşik makineleri oluşturur.
– Basit makineler kuvvetin yönünü, büyüklüğünü ve
uygulama noktasını değiştirerek iş yapma kolaylığı sağlar.
– Hiçbir basit makine işten kazanç sağlamaz.
– İdeal bir basit makinede kuvvetin yaptığı iş, yükün
kazandığı enerjiye eşittir.
23
Basit Makineler
1. Kaldıraçlar
a)
b)
Çift taraflı kaldıraç
Tek taraflı kaldıraç
2. Makaralar
a)
b)
3.
4.
5.
6.
7.
8.
Sabit makaralar
Hareketli makara
Eğik düzlem
Vida
Çıkrık
Dişli
Kasnak
Kama
24
1. Kaldıraçlar
Sabit bir destek etrafında dönebilen çubuklardan
oluşmuş sistemlere kaldıraç denir.
Desteğin ortada, yük ve kuvvetin iki uçta olduğu
kaldıraçlara çift taraflı kaldıraç denir.
Desteğin uçta olduğu; yükün ortada, kuvvetin
diğer uçta ya da kuvvetin ortada, yükün diğer uçta
olduğu kaldıraçlara da tek taraflı kaldıraç denir.
25
Kaldıraç Çeşitleri
26
Kaldıraçlar (Soru)
Ağırlığı önemsiz çubukla kurulan şekildeki
kaldıraçta P yükü F kuvvetiyle dengelenmiştir.
Buna göre F kuvveti kaç N’dur?
A) 25 B) 50 C) 100 D) 200
27
2. Makaralar
Makaralar sabit ve hareketli olmak üzere
ikiye ayrılırlar.
28
Sabit makara
Sabit makaralar kuvvetten
kazanç sağlamaz, sadece kuvvetin
yönünü değiştirir.
İp h kadar çekildiğinde yük h
kadar yükselir. Yani doğru orantılı
bir ilişki vardır.
Özellikle inşaatlarda
malzemeyi yukarı almak
için kullanılır.
29
Sabit makara (Soru)
Şekilde
verilen
makarada
yük
dengededir.
Makaranın ağırlığı 4N olduğuna göre,
makarayı tavana bağlayan ipte oluşan
gerilme kaç N’dur?
A) 20
B) 24
C) 32
D) 36
30
Hareketli makara
Hem dönebilen hem de
yükselip alçalabilen makaradır.
Makara yükle birlikte hareket eder.
Yükün h kadar yukarı çekilmesi için
2h kadar ipin çekilmesi gerekir.
Makara ağırlığı ve sürtünmeler
önemsiz ise;
31
Hareketli makara (Soru)
Makara ağırlıklarının 2N olduğu
şekildeki sistemde F kuvveti kaç
N’dur?
A) 5
B) 5,5
C) 6
D) 6,5
32
Palangalar
Bu gördüğümüz sabit ve hareketli
makaralardan oluşan karma sistemlere de
palangalar denir. Kuvvet yönüne göre 2 çeşittir.
Kuvvet yönü
aşağı doğru ise,
Kuvvet yönü
aşağı doğru ise,
F = P / Yukarı
doğru
İp sayısı
F = P / Yukarı
doğru
İp sayısı
33
3. Eğik düzlem
Ağır yükleri belli yüksekliğe kaldırmak zor olduğu zaman
eğik düzlem yardımıyla yükten daha az bir kuvvet ile cisimler
istenilen yüksekliğe çıkarılabilir.
Sürtünmeler önemsiz ise, eğik
düzlemde iş prensibi geçerlidir.
Kuvvet . Kuvvet yolu = Yük . Yük yolu
F.S = P.h
Kuvvet yolu, kuvvete paralel
olan S yolu, yük yolu ise, yüke paralel
olan h yoludur. Kuvvetten kazanç
sağlanır. Fakat aynı oranda yoldan kayıp
olur.
34
35
Eğik düzlem (Soru)
Şekildeki eğik düzlemde
taşıyabilen F kuvveti kaç N’dur?
A) 20
B) 25
C) 30
D) 45
45N’luk
yükü
36
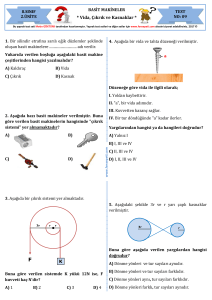
4. Vida
Vida, iki yüzeyi birbirine birleştirirken, en çok
kullanılan, basit makinelerden birisidir. Vidada iki diş
arasındaki uzaklığa vida adımı denir.
Vida başı bir tam dönüş yaptığında vida, vida
adımı (a) kadar yol alır. N kez döndüğünde ise N . a
kadar yol alır.
Vidayı döndürmek için uygulanan F kuvvetinin
yaptığı iş, vida tahtaya girerken R direngen kuvvetinin
yaptığı işe eşittir.
Vidanın baş kısmı daire olduğu için bir turda
kuvvet yolu dairenin 2πr çevre uzunluğu kadar olur.
İş prensibinden,
Kuvvet . Kuvvet yolu = Yük . Yük yolu
F . 2πr = R . a
Kuvvet kazancı = P/F
= 2πr/a
37
Vida (Soru)
Vida adımı 4 mm olan bir vida 8 tam dönüş
yaptığında saplandığı yüzeyde kaç cm ilerler?
A) 1,2
B) 2,2
C) 3,2
D) 6,4
38
5. Çıkrık
Merkezleri çakışık ve merkezlerinden
geçen eksen etrafında dönen iki silindir ya
da ortak eksenli bir silindir ve bir koldan
oluşan düzeneklerdir.
Yükün aldığı yol (h), çıkrığın devir sayısı
(N) ile çıkrık silindirinin çevresine (2πr)
bağlıdır.
h = N. 2πr
Çıkrığın çalışma prensibi kaldıracın ki
ile aynıdır.
Kuvvet . Kuvvet kolu = Yük . Yük kolu
F.R = P.r
39
Çıkrık (Soru)
Büyük silindirin yarıçapı küçük
silindirinkinin dört katı olan
şekildeki çıkrıkta 5N’luk kuvvet ile
taşınabilecek en büyük yük kaç
N’dur?
A) 5
B) 10
C) 15
D) 20
40
6. Dişliler
Dönme yönünü ve
dönme hızını değiştiren,
üzerinde dişer bulunan
basit makinelerdir.
41
Dişliler (Soru)
Yarıçapları sırasıyla r,3r,2r olan
X, Y, Z dişlilerinden X ok yönünde 4
tur dönerse Z dişlisi hangi yönde kaç
tur döner?
A) 1 yönünde, 4 tur
B) 1 yönünde, 6 tur
C) 2 yönünde, 3 tur
D) 2 yönünde, 6 tur
42
7. Kasnaklar
Dişliler gibi dönme yönünü ve hızını değiştiren, birbirine
kayışlarla bağlanan basit makinelerdir.
Bağlanma yönü ters de olsa düz de olsa dişlilerde olduğu gibi
tur sayısı (n), yarıçapla (r) ters orantılıdır.
n1 . r1 = n2 . r2
Eş merkezli (en sağdaki) kasnaklarda ise tur sayıları ve dönüş
yönleri aynıdır.
n1 = n2
43
Kasnaklar (Soru)
Şekildeki düzenekte X
kasnağı ok yönünde 3 tur
dönerse Y kasnağı hangi
yönde kaç tur döner?
A) 1 yönünde, 1tur
B) 1 yönünde, 2 tur
C) 2 yönünde, 3 tur
D) 2 yönünde, 4 tur
44
8. Kama
İki tane eğik düzlemin
tabanlarından birleşmesiyle
elde edilen düzenek kama
olarak adlandırılır.
Balta, bıçak, çivi ucu
kamaya örnek gösterilebilir.
Kamanın eğik düzlemden
farkı,
cisim
duruyorken
kamanın hareket etmesidir.
45
Ünitenin Kavram Haritası
46