Elektrik Devrelerinin Temelleri

Elektrik Devrelerinin Temelleri
Neslihan Serap Şengör
Devreler ve Sistemler A.B.D.
oda no:1107 tel no:0212 285 3610
[email protected]
Ders Hakkında
• 1 Yarıyıl içi sınavı
•
3 Kısa sınav
25 Kasım 2012
% 30
21 Ekim
11 Kasım
9 Aralık
• 1 Ödev
% 30
+5
• Yarıyıl Sonu Sınavı
% 40
Ders notlarına ve ders ile ilgili bazı dökümanlar erişmek için
Ninova – ELE 211 - Dersin kaynakları
http://ninova.itu.edu.tr/tr/dersler/elektrik-elektronik-fakultesi/897/ele-211/ekkaynaklar?u266985/ust-klasor
FİNAL SINAVINA GİRMEYE HAK KAZANMAK İÇİN YARIYIL İÇİ
DEĞERLENDİRMELERİNDEN EN AZ 15 ALMAK GEREKMEKTEDİR.
Kaynaklar:
Yılmaz Tokad, “ Devre Analizi Dersleri” Kısım I, Çağlayan
Kitabevi, 1986.
Cevdet Acar, “Elektrik Devrelerinin Analizi” İ.T.Ü. Yayınları,
1995.
L.O. Chua, C.A. Desoer, S.E. Kuh. “Linear and Nonlinear Circuits”
Mc.Graw Hill, 1987, New York ( İşlenen Bölümler: 1-8, 12)
Elektrik Devrelerinin Temelleri dersinde ne yapacağız?
Amaç: Fiziksel devrelerin elektriksel davranışlarını öngörme
akım ve gerilim
http://homepages.wmich.edu/~miller/
http://sinhardware.com/index.php/site-map/motherboards/gigabyte/lga1155-z77/97-g1-sniper-3/g1-sniper-3-review/78-g1-sniper-3review?showall=&start=3
http://fog.ccsf.org/~wkaufmyn/ENGN20/ENGN20.html
Uygulama alanı: boyut bir fikir verebilir
gerilim μV
MV
akım fA
MA
frekans 0 Hz
güç 10-14 W
http://vertikahelio.com/About.html
1GHz
109 W
http://www.sandc.com/news/index.php/2004/01/turnkey
-circuit-switcher-and-trans-rupter-ii-installations-improvesystem-reliability/
Fiziksel Devre ...
http://www.drchaos.net/drchaos/Papers/io_7.pdf
... ve modeli
Teori oluştururken işe nasıl başlarız?
Tanımlanmamış büyüklükler
Aksiyomlar
Sonra ne yaparız?
Yeni büyüklükler için: Tanımlar
Yeni sonuçlar için: Teoremler
Elektrik Devre Teorisi
Tanımlanmamış büyüklükler
Akım
Gerilim
i(t) [A]
Uyarma
Devresi
v(t) [V]
+
_
A
+
_
V
Nasıl ölçeceğimize dikkat etmemiz gerekiyor
uyumlu çift tanımlanacak
akım ve gerilim
1
+
1
İ1 (t)
v1 (t)
2
_
+
V2
İ1 (t)
İ2 (t)
3- uçlu
eleman
_
Kaç ucu var?
iki uçlu eleman
i1(t0)=2A
i1(t1)=-5A
v1(t0)=2A
v1(t1)=-32V
İ3 (t)
_
+
3
+_
2
Aksiyomlar
Ne demek?
1. Toplu Parametreli Devre
Fiziksel devrede her aletin uçlarındaki akım i(t) ve gerilim v(t)
her t anında tam olarak tanımlanmışsa, devre toplu parametreli devredir.
Kirchhoff’un Gerilim Yasası (1845)
Önce biraz hazırlık
• n düğümü olan toplu parametreli, birleşik bir devrede
herhangi bir düğümü referans düğümü olarak seç.
• seçilen referans düğümüme göre n-1 tane düğüm gerilimi
tanımla
1
3
+
+
e1 e2
e3
. . . k
+.
ek
__ _
__
en=0 n
Vkn-1
1824-1887
Königsberg Üniversitesi
Berlin Üniversitesi
Breslau Üniversitesi
Heidelberg Üniversitesi
+
2
. .
+
en-1
• k. düğüm ile j. düğüm
arasındaki gerilim farkı: vkj
n-1
2. Kirchhoff’un Gerilim Yasası (KGY)
Tüm toplu parametreli birleşik devrelerde referans düğümü keyfi
seçilmek üzere tüm k, j düğüm çiftleri için, her t anında
vkj (t )  ek (t )  e j (t )
bağıntısı geçerlidir.
2. Kirchhoff’un Gerilim Yasası (KGY)
Tüm toplu parametreli birleşik devrelerde tüm kapalı düğüm
dizileri için, her t seçilen kapalı bir düğüm dizisi için düğümden
düğüme gerilimlerin cebirsel toplamı sıfırdır.
Burada ters olan bir şey var, nedir?
Teorem:
Tanıt:
Düğüm gerilimleri cinsinden
KGY
Kapalı düğüm dizileri cinsinden
KGY
 Düğüm gerilimleri cinsinden KGY
Kapalı düğüm dizileri cinsinden KGY ?
Bir düğüm dizisi oluşturalım
a-b-c-d-a
Her hangi bir t anında seçilen kapalı düğüm dizisi için
düğümden düğüme gerilimlerin cebirsel toplamını yazalım
vab  vbc  vcd  vda
vab  ea  eb
Bu nasıl yazıldı?
vbc  eb  ec
vcd  ec  ed
vda  ed  ea
 Düğüm gerilimleri cinsinden
KGY
ea  eb  eb  ec  ec  ed  ed  ea  0
 Kapalı düğüm dizileri cinsinden KGY
p-q-r-p
v pq  vqr  vrp  0
r düğümünü referans seçelim
Bu nasıl yazıldı?
vqr  eq
vrp  e p
v pq  eq  (e p )  0
v pq  e p  eq
Kirchhoff’un Akım Yasası (KAY)
+
_
Gauss Yüzeyi
içi ve dışı tanımlı, sadece devre elemanlarını
birleştiren bağlantıları kesecek şekilde çizilmiş
yüzey
3. Kirchhoff’un Akım Yasası (KAY)
Tüm toplu parametreli devrelerde, tüm Gauss yüzeyleri için her t
anında Gauss yüzeyini kesen akımların cebirsel toplamı sıfırdır.
3. Kirchhoff’un Akım Yasası (KAY) (Düğümler için)
Tüm toplu parametreli birleşik devrelerde, her t anında, herhangi
bir düğümden çıkan akımların cebirsel toplamı sıfırdır.
Burada da ters olan bir şey var, nedir?
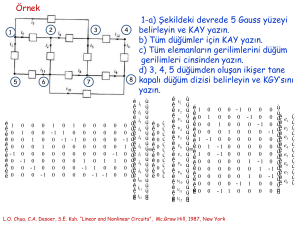
Örnek
2
1
5
6
3
7
4
8
1-a) Şekildeki devrede 5 Gauss yüzeyi
belirleyin ve KAY yazın.
b) Tüm düğümler için KAY yazın.
c) Tüm elemanların gerilimlerini düğüm
gerilimleri cinsinden yazın.
d) 3, 4, 5 düğümden oluşan ikişer tane
kapalı düğüm dizisi belirleyin ve KGY’sını
yazın.
L.O. Chua, C.A. Desoer, S.E. Kuh. “Linear and Nonlinear Circuits”, Mc.Graw Hill, 1987, New York