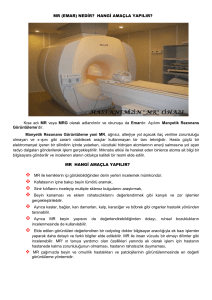
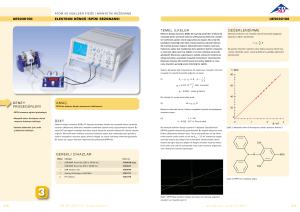
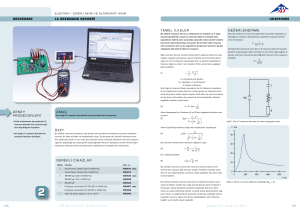
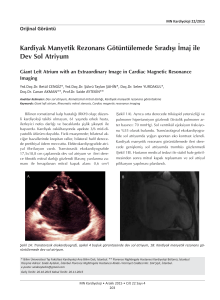
𝐼2 = 𝐼1 (
𝑗𝐿𝑚 𝜔
𝑗𝐿2 𝜔+(
1
)+𝑍0 +𝑅
𝑗𝜔𝐶
)
1
𝑉1 = 𝐼1 . (𝑅 + 𝑗𝐿1 𝜔 + (𝑗𝜔𝐶 )) − 𝐼1 (
𝑗𝐿𝑚 𝜔
𝑗𝐿2 𝜔+(
𝑗 2 𝐿𝑚 2 𝜔 2
1
𝑉1 = 𝐼1 . [(𝑅 + 𝑗𝐿1 𝜔 + (𝑗𝜔𝐶 )) − (
𝑗𝐿2 𝜔+(
1
1
)+𝑍0 +𝑅
𝑗𝜔𝐶
𝐿𝑚 2 𝜔 2
1
𝑍𝐸ş = 𝑍𝐺𝑖𝑟𝑖ş = 𝑅 + 𝑗𝐿1 𝜔 + (𝑗𝜔𝐶 ) + (
𝑍𝐸ş = 𝑅 + 𝑗𝐿1 𝜔 + (𝑗𝜔𝐶 ) + (
1
)+𝑍0 +𝑅
𝑗𝜔𝐶
𝑗𝐿2 𝜔+(
𝐿𝑚 2 𝜔 2
𝑗𝐿2 𝜔+(
1
𝑍𝐸ş = 𝑅 + (𝑗𝜔𝐶 ) + 𝑗(𝐿1 − 𝐿𝑚 )𝜔 +
1
𝑍𝐸ş = 𝑅 + (𝑗𝜔𝐶) + 𝑗(𝐿1 − 𝐿𝑚 )𝜔 +
1
)+𝑍0 +𝑅
𝑗𝜔𝐶
)
) + 𝑗𝐿𝑚 𝜔 − 𝑗𝐿𝑚 𝜔
−𝑗 2 𝐿𝑚 2 𝜔 2 +𝑗 2 𝐿𝑚 𝐿2 𝜔 2 +𝑗𝐿𝑚 𝜔(𝑍0 +𝑅)+𝑗𝐿𝑚 (
𝑗𝐿2 𝜔+(
(𝑗𝐿𝑚 𝜔)(𝑗(𝐿2 −𝐿𝑚 )𝜔+(
𝑗𝐿2 𝜔+(
1
)+𝑍0 +𝑅
𝑗𝜔𝐶
1
)+𝑍0 +𝑅)
𝑗𝜔𝐶
1
)+𝑍0 +𝑅
𝑗𝜔𝐶
1
1
𝑗𝐿2 𝜔+(
)+𝑍0 +𝑅+𝑗𝐿𝑚 𝜔−𝑗𝐿𝑚 𝜔
𝑗𝜔𝐶
1
(𝑗𝐿𝑚 𝜔)(𝑗(𝐿2 −𝐿𝑚 )𝜔+(
)+𝑍0 +𝑅)
𝑗𝜔𝐶
1
𝑍𝐸ş = 𝑅 + (𝑗𝜔𝐶 ) + 𝑗(𝐿1 − 𝐿𝑚 )𝜔 +
)]
1
)+𝑍0 +𝑅
𝑗𝜔𝐶
1
𝑍𝐸ş = 𝑅 + (𝑗𝜔𝐶 ) + 𝑗(𝐿1 − 𝐿𝑚 )𝜔 +
)(𝑗𝐿𝑚 𝜔)
1
1
1
+
𝑗𝐿𝑚 𝜔 𝑗(𝐿2 −𝐿𝑚 )𝜔+(1/𝑗𝜔𝐶)+𝑍0 +𝑅
Tekrar düzenlenirse,
1
𝑉1 = 𝐼1 . (𝑅 + 𝑗𝐿1 𝜔 + (𝑗𝜔𝐶 )) − 𝐼2 . (𝑗𝐿𝑚 𝜔)
1
0 = 𝐼2 . (𝑗𝐿2 𝜔 + (𝑗𝜔𝐶 ) + 𝑍0 + 𝑅) − 𝐼1 . (𝑗𝐿𝑚 𝜔)
𝐼2 = 𝐼1 (
𝑗𝐿𝑚 𝜔
𝑗𝐿2 𝜔+(
1
)+𝑍0 +𝑅
𝑗𝜔𝐶
idi. Buna göre;
)
𝑍𝐸ş = 𝑍𝐺𝑖𝑟𝑖ş = 𝑅 + 𝑗𝐿1 𝜔 + (
1
𝐿𝑚 2 𝜔2
)+(
)
1
𝑗𝜔𝐶
𝑗𝐿2 𝜔 + (𝑗𝜔𝐶 ) + 𝑍0 + 𝑅
1
)𝜔
𝑗𝜔𝐶
Burada IÇıkış akımı alıcıdan gecen akıma I2’ye eşit, IGiriş akımı vericiden geçen akıma I1’e eşit, ZÇıkış
empedansı ZYük empedansına eşittir. Çıkış akımının giriş akımına oranı için;
𝐼Ç𝚤𝑘𝚤ş
𝐼𝐺𝑖𝑟𝑖ş
=
𝑗𝐿𝑚 𝜔
𝑗𝐿2 𝜔+(
1
)+𝑍0 +𝑅
𝑗𝜔𝐶
(6)
Verim denkleminde yerlerine yazılırsa;
𝐼2
𝑃
∗𝑍Ç𝚤𝑘𝚤ş
ɳ = 𝑃Ç𝚤𝑘𝚤ş = 𝐼Ç𝚤𝑘𝚤ş
2
∗𝑍
𝐺𝑖𝑟𝑖ş
ɳ=(
𝐺𝑖𝑟𝑖ş
𝑗𝐿𝑚 𝜔
𝐺𝑖𝑟𝑖ş
1
𝑗𝐿2 𝜔+(
)+𝑍0 +𝑅
𝑗𝜔𝐶
)2
𝑍0
1
𝐿𝑚 2 𝜔2
(𝑅+𝑗𝐿1 𝜔+(
)+(
))
1
𝑗𝜔𝐶
𝑗𝐿2 𝜔+(
)+𝑍0 +𝑅
𝑗𝜔𝐶
Görüldüğü gibi sistemin verimi; iç direnç, alıcı ve verici bobinlerin endüktansları ile karşıt
endüktasa bağlıdır. Maksimum verim için Lm karşıt endüktans, L alıcı ve verici endüktans, Z0
karakteristik empedans ve R endüktans ve kapasite iç direncini tanımlar. (1) numaralı eşitlik
durumu altında verimin maksimum olması mümkündür. (2) numaralı eşitlik durumunda sistem
çift rezonans frekansına sahiptir. (3) numaralı eşitlik durumunda ise sistem düşük bir verimle tek
rezonans frekansına sahiptir.
𝐿2𝑚 =
𝐿2𝑚 >
𝐿2𝑚 <
𝑍02 −𝑅 2
(1)
𝜔02
𝑍02 −𝑅 2
(2)
𝜔02
𝑍02 −𝑅 2
(3)
𝜔02
𝑍𝐸ş = 𝑍𝐺𝑖𝑟𝑖ş = 𝑅 + 𝑗𝐿1 𝜔 + (
1
)+(
𝑗𝜔𝐶
𝐿𝑚 2 𝜔2
1
𝑗𝐿2 𝜔+(𝑗𝜔𝐶)+𝑍0 +𝑅
) idi.
Verim denklemini kullanarak verimin frekansa göre değişimini incelersek bir verim-frekans grafiği
elde ederiz. ZEş eşdeğer empedans denklemini kullanarak eşdeğer empedansın frekansa göre
çizdirirsek bir eşdeğer empedans-frekans grafiği elde ederiz. Bu iki grafiği karşılaştırmak adına iki
grafiği üst üste çizdirdiğimizde üç rezonans frekansı durumu elde ederiz.
Üç rezonans frekanslı KET sisteminin verim-frekans ve eşdeğer empedans-frekans grafiği
Tek rezonans frekanslı KET sisteminin verim-frekans ve eşdeğer empedans -frekans grafiği
İlk grafik incelendiğinde verimin maksimum olduğu 3 adet rezonans frekansı vardır. 1. ve 3.
rezonans noktaları bizim kullandığımız rezonans noktalarıdır. Ama 2. rezonans noktası istenilen
bir rezonans frekansı noktası değildir. Bunun sebebi ise 2. rezonans frekansının eşdeğer
empedansına bakıldığında Zeş2>Zeş1=Zeş3 olduğu görülmektedir. Pgiriş (𝑃𝑔𝑖𝑟𝑖ş =
2
𝑉𝑔𝑖𝑟𝑖ş
𝑍𝐸ş
) ZEş eşdeğer
empedans ile ters orantılı olduğundan 2. rezonans frekansı noktasında (ZEş büyük olduğundan
Pgiriş küçülür) yüksek güçte bir enerji aktarımı olmaz. Bu yüzden 2. rezonans frekansı istenilen bir
çalışma değildir. İlk grafikte 1. ve 3. rezonans frekanslarına ikinci grafikte ise tek olan rezonans
frekansı noktasına bakıldığında, bu noktaların sistemin veriminin en yüksek ve eşdeğer
empedansın en düşük olduğu noktalar olduğu görülmektedir. Eşdeğer empedansın minimum
olması demek bu çalışma için eşdeğer empedansın endüktif yada kapasitif değil sadece omik
bileşeni olduğu anlamına gelmektedir. Bu kuraldan yola çıkarak sistemi omik yapan rezonans
frekansı yakalanmaya çalışılır.
M
Cs
Rg
Ls
Cd
Ld
RL
Vg
Rs
Rd
Şekil 3.2 Bağlantılı rezonatör sisteminin eşdeğer devresi
Burada kaynak Rg iç dirençli, ω frekansında, Vg genlikli sinüsoidal gerilim kaynağıdır. Kaynak ve
cihaz rezonatör bobinleri Ls ve Ld, karşıt endüktans M (𝑀 = 𝑘√𝐿𝑠 𝐿𝑑 ) ile gösterilir. Bir rezonatör
oluşturmak için her bir bobine seri bir kapasitör vardır. Rs ve Rd dirençleri, her bir rezonatör için
bobinlerin ve rezonans kondansatörlerinin istenmeyen (omik ve ışınım kayıplarını içeren)
dirençleridir. Yük AC direnç RL ile gösterilir.
Bu devrenin verimi, kaynak ve cihaz rezonanstayken yük direncine gönderilen gücün kaynakdaki
maksimum mevcut güce oranı ile bulunur.
𝑃𝐿
𝑃𝑔,𝑚𝑎𝑥
𝑈=
4𝑈 2
=
[(1+
𝜔𝑀
√𝑅𝑠 𝑅𝑑
𝑅𝑔
𝑅𝑠
𝑅𝑔 𝑅𝐿
𝑅𝑠 𝑅𝑑
𝑅
)(1+ 𝐿 )+𝑈 2 ]
𝑅𝑑
= 𝑘√𝑄𝑠 𝑄𝑑
2
En iyi sistem performansı sağlamak için yük ve kaynak dirençleri uygun seçilebilir ya da empedans
dönüşüm bağlantısı kullanılarak diğer direnç değerleri yakalanabilir. Eğer dirençler denklem
(3.5)’teki gibi seçilirse,
𝑅𝑔
𝑅𝑠
=
𝑅𝐿
𝑅𝑑
= √1 + 𝑈 2
güç aktarımı verimi denklemi
ɳ𝑜𝑝𝑡 =
𝑈2
(1+√1+𝑈 2 )
2
U fonksiyonuna bağlı enerji aktarımının optimum verimi grafiği
Burada U değerleri büyük olan sistemlerde yüksek verimle enerji aktarımının mümkün olduğu
görülmektedir. Mümkün olan en iyi kablosuz enerji aktarımı sistemi verimi, sistemin
performansını belirleyen fakörler olan; rezonatörler arasındaki magnetik kuplaj katsayısı k ve
yüksüz rezonatörlerin kalite faktörüne Qs (kaynak) ve Qd (cihaz) bağlıdır.
Bir kablosuz güç aktarım sisteminin başarımı başlıca iki parametre ile belirlenir: Primer akımı (Ip)
nedeniyle sekonderde (alıcı endüklenen ω frekanslı açık devre gerilimi V OC. Bir diğeri ise, bu
gerilimin yarattığı kısa devre akımı Isc. Bu akım, sargıdan akabilecek en büyük akımdır.
Sargıdan alınan güç ise aşağıdaki eşitlik ile bulunabilir.
Bu aktif gücün en yüksek değeri, yük direnci sargı empedansına eşitken elde edilir:
Bu durumda gücün en yüksek değeri:
Sargı gücü ise aşağıdaki şekilde olur.
Maksimum güç için Voc, Isc ve R eşitlikleri kullanılarak;
yazılabilir. Maksimum gücün aktarılması isteniyorsa sargının kompanze edilmesi gerekir.
Sekonder tarafın bir kondansatör yardımıyla kompanzasyonun gerçekleştirilmiş olduğu
varsayıldığında, eşitlikler aşağıdaki şekilde yeniden yazılabilir.
Eğer kondansatör değeri uygun bir şekilde seçilirse reaktif elemanlar birbirlerinin etkilerini yok
edeceğinden,
olur.
Voc, Isc Isargı ve Vsargı eşitlikleri güç eşitliğinde yerine yazılırsa güç aşağıdaki biçimde bulunur.
Reaktif elemanların kalite katsayısı, elamanda depolanan enerjinin, elemanın aktif gücüne oranı
olarak tanımlanır. Örneğin iç direnci Rs olan bir endüktans için bu katsayı
olur. Seri bağlı sekonder devresi için kalite katsayısı aynı biçimde tanımlanabilir. Sargının iç
direncinin yük direnci yanında ihmal edilebilecek kadar küçük olduğu kabul edilirse, sekonder
sargısının kalite katsayısı (Qs ) şu biçimde tanımlanır.
Seri kompanzasyonlu sekonder sargısı için güç kalite faktörü cinsinden
Buna göre maksimum aktif güç:
olur.
Görüldüğü üzere, sargıdan alınabilecek aktif güç, kalite faktörüne bağlı olarak artabilmektedir.
Açık devre gerilimi ve kısa devre akımı yerine konulursa, seri kompanzasyonlu devre için
maksimum güç ifadesi aşağıdaki gibi olur.
Hareketsiz bir sistemde M ve L sabit olduğundan, aktarılacak gücün en yüksek yapılması için ωIp
değerinin yüksek olması gerekir. Sistemin maliyetini ve karmaşıklığını etkileyen bir diğer faktör
çalışma frekansıdır. Belirli Ip M Ls değerleri için aktarım oranı doğrudan frekansa bağlıdır.
Günümüz güç elektroniği sistemlerinde kilowattlar mertebesindeki güçler için çalışama frekansı
10kHz-100kHz aralığındadır. Bu frekans aralığında deri etkisi ve yakınlık olayının dikkate alınması
gerekir. Bu nedenle Litz sargılar kullanılır.