T.C
ERZURUM TEKNİK ÜNİVERSİTESİ
MÜHENDİSLİK ve MİMARLIK FAKÜLTESİ
İnşaat Mühendisliği Bölümü
MMF-201
MALZEME BİLİMİ
DERS NOTLARI
Yrd. Doç. Dr. Türkay KOTAN
ERZURUM - 2016
1
Hafta
Konular
1
Giriş, atomik yapı, atomlararası bağlar, malzemelerin sınıflandırılması
2
Kristal yapı, miller indisleri
3
Kristal kusurları ve katılarda yayınım
4
Faz dönüşümleri ve faz diyagramları
5
Malzemelerin fiziksel özellikleri
6
Malzemelerin mekanik özellikleri
7
Malzemelerin mekanik özellikleri
8
Mekanik deneyler
9
Malzemelerin elektriksel ve manyetik özellikleri
10
Malzemelerin optik ve ısıl özellikleri
11
Aşınma ve korozyon
12
Mühendislik malzemeleri, metaller (demir ve demir dışı)
13
Seramikler, camlar, plastikler
14
Polimerler, kompozitler
Sayı
Kaynaklar
1
Malzeme Bilimi, Bilim ve Teknik Yayınevi, Prof. Dr. Kaşif ONARAN, 1995.
2
Malzeme Bilimi ve Mühendisliğine Giriş, Çeviri: Prof. Dr. Kenan Genel
3
Materials Science and Engineering an Introduction, W.D. Callister Jr.
2
MALZEME BİLİMİ
Giriş, Atomik Yapı
MALZEMENİN ÖNEMİ ve MALZEME BİLİMİ
MALZEME; genel anlamda, doğada canlıların ihtiyacına yönelik bir amaç için kullanılan, doğal yada
yapay olarak üretilmiş maddelerdir. Teknik anlamda ise, mühendislik uygulamalarında kullanılan katı
maddelere malzeme adı verilir.
Örneğin; insanların enerji ihtiyacını karşılamak için inşa edilen bir dolgu baraj yapımında doğal toprak
ve kaya malzemeleri kullanılırken, insanların barınma ihtiyacını karşılamak için inşa edilen bir bina
inşaatında beton, çelik, ahşap, cam ve plastik gibi yapay olarak üretilen malzemeler kullanılabilir.
Malzeme, insanoğlunun tarihsel gelişiminde hep önemli bir yere ve etkiye sahip olmuştur. Öğle ki, her
dönemin teknolojisi ve bir anlamda uygarlığı o dönemde kullanılan malzemelerle sınırlanmıştır. Tarih
öncesinde yaşanan taş, bakır, bronz (tunç) ve demir çağları buna örnek olarak verilebilir. Nitekim
malzeme kullanıldığı çağa adını verecek kadar insanlık tarihinde önemli bir yer tutmaktadır.
MALZEME BİLİMİ; insanların yararlanabileceği malzemelerin yapısını, özelliklerini ve davranışlarını
inceleyen, doğal veya yapay hammaddelerden seramik, polimer ve metal alaşımları gibi yeni
mühendislik malzemelerinin üretimini araştıran ve çeşitli sanayi dallarında kullanımını sağlayan bilim
dalıdır.
Malzeme ve malzeme biliminin mühendisler için önemini kavramak için mühendislik mesleğinin
tanımına ve mühendisin sorumluluklarına değinmek gerekir.
Mühendislik mesleğinin tanımından bilindiği üzere; mühendisler, insanlar için toplumsal yaşamın
gerektirdiği beslenme, barınma, korunma, ulaşım, enerji ve iletişim gibi somut ihtiyaçları karşılamak
amacıyla, bilimin ve fennin ışığında ekonomik ve fonksiyonel çözümler, teknikler ve yöntemler
geliştirerek, bunların hayata geçirilmesinde hizmet veriler.
Bu hizmetlerin araştırma veya tasarım sürecinde karar verici, uygulama sürecinde ise organizasyon ve
kontrol sorumluluklarını üstlenen çeşitli mühendislik dalları için malzemeler, kimi zaman incelenen,
çoğu zaman da kullanılan ortak bir materyaldir.
Örneğin, insanların barınma, ulaşım ve enerji gibi ihtiyaçlarını karşılamak için binalar, yollar ve barajlar
gibi yapıları inşa etmekle sorumlu inşaat mühendisleri, bu yapıları toprak ve kaya malzemelerinden
oluşan zemin üzerine inşa ederken, yapıların inşasında da beton, agrega, çelik, taş, ahşap ve çelik
gibi daha birçok malzemeyi kullanırlar.
Dolayısıyla, diğer mühendislik dallarında olduğu gibi inşaat mühendisleri de, çözümlerini
gerçekleştirmek için yararlanmak zorunda oldukları çeşitli yapı malzemelerinin özelliklerini tanımak ve
davranışlarını bilmek zorundadırlar.
Öğle ki, mühendislik yapılarından beklenen; güvenlik, ekonomiklik, işlevsellik, estetiklik ve kalıcılık
nitelikleri, ancak doğru tasarım ve yöntemler yanında, amaca uygun malzemelerin kullanılması ve
gerekli tedbirlerin alınmasıyla sağlanabilir. Bu da, mühendislerimizin yeterli düzeyde malzeme bilgisine
sahip olmasıyla mümkündür.
1
MALZEME BİLİMİ
Giriş, Atomik Yapı
MALZEMELERİN İÇYAPISI (ATOMİK YAPI)
Doğadaki tüm maddeler gibi, malzemeler de atom veya atom gruplarından (molekül) oluşur. Nitekim
malzemeleri öğrenmek için önce atomun yapısını, özelliklerini ve davranışlarını anlamak gerekir.
MADDE; uzayda yer kaplayan, belirli bir hacmi ve kütlesi olan tanecikli yapılardır.
ATOM; maddelerin en küçük yapıtaşıdır.
MOLEKÜL; Aynı veya farklı tür en az iki atomun birleşmesiyle oluşmuş atom kümeleridir.
ELEMENT; kimyasal çözümlemeyle ayrıştırılamayan veya bireşim yoluyla elde edilemeyen aynı cins
atomlardan meydana gelmiş saf maddelerdir.
Bir atomun yapısı, proton ve nötronları barındıran bir çekirdek ile bu çekirdek etrafındaki yörüngelerde
hareket halindeki elektron parçacıklarından oluşur.
Bir atomun ağırlığı, çekirdeğini oluşturan pozitif elektrikle yüklü protonlar ve yüksüz (nötr) olan
nötronların ağırlıkları toplamına eşittir. Negatif elektrikle yüklü elektronların kütleleri ise atomun
ağırlığına katkıları ihmal edilecek kadar küçüktür.
Nötr bir atomda elektronların sayısı protonların sayısına eşittir, yani toplam elektriksel yük sıfırdır.
Bir atomda bulunan protonların sayısı o atomun atom numarasını belirler. Atomun kütle numarası ise
proton ve nötronların toplam sayısına eşittir.
Örneğin; SODYUM (Na) atomunun çekirdeğinde 11 proton ile 12 nötron ve çevresindeki 3 yörüngede
toplam 11 elektron bulunduğundan atom numarası 11, kütle numarası ise 11p+12n=23 dür.
Malzemeyi oluşturan atom veya atom kümelerinin, aralarında var olan bağ kuvvetleri etkisinde bir
araya gelerek, uzayda üç boyutlu olarak dizilmeleri şeklindeki oluşum İÇYAPI yada ATOMİK YAPI
olarak adlandırılır.
Malzemelerin özellikleri içyapılarına büyük ölçüde bağlıdır. Malzemelerin içyapıları ise içerdikleri
atomların cinsine, dizilişine ve birbirlerine bağlanış biçimlerine göre değişir.
Öğle ki bir cismin kimyasal bileşimi aynı kaldığı halde atomik diziliş biçimi değişirse özellikleri de büyük
ölçüde değişir.
Örneğin; %0,8 karbonlu çelik 800 oC sıcaklıkta ısıtıldıktan sonra 1 günde 1 saatte ve 1 saniyede olmak
üzere üç farklı hızda soğutulacak olursa, mukavemetler yaklaşık 1/2/3 oranında farklı değerler alır.
Bunun nedeni, üç farklı soğuma hızında atomların değişik biçimde dizilmesi, dolayısıyla üç değişik
içyapı oluşmasıdır. Mikroskopla incelendiğinde bu farklar açık bir şekilde görülebilir.
2
MALZEME BİLİMİ
Giriş, Atomik Yapı
Atomun yapısında elektronlar atom çekirdeği çevresinde belirli yörüngeler üzerinde sürekli hareket
halindedirler ve belirli bir enerji düzeyine sahiptirler.
Elektronlar çekirdek çevresindeki yörüngelere yerleşirken önce en düşük enerji düzeyini doldururlar.
Ancak tek yörüngeli atomlarda bir enerji düzeyinde en fazla iki elektron, çok yörüngeli atomlarda ise
en dış yörüngede en fazla 8 elektron bulunabildiğinden, elektronların sayıları arttıkça sırasıyla daha
dıştaki bir enerji düzeyine (yörüngeye) geçerler. Bir enerji düzeyinde bulunan bir elektrona yeterli
enerji verilirse boş olan bir üst enerji düzeyine atlayabilir. Nitekim her atom türünün elektron yapısı ve
enerji düzeyleri farklıdır.
Atomların bir arada tutularak maddeleri oluşturması atomlararası bağlar tarafından sağlanır.
ATOMLARARASI BAĞLAR
Atomlararası bağ kuvvetleri atomları bir arada tutarak içyapıyı oluşturur. Atomlararası bağ
kuvvetlerinin oluşmasındaki ana etken ise atomların elektron yapılarıdır.
Özellikle en dış yörüngede bulunan valans elektronları cisimlerin mekanik, fiziksel ve kimyasal
özelliklerini belirler.
Atomlararası bağlar kuvvetli olursa malzemenin elastisite modülü, mukavemeti ve ergime sıcaklığı
yüksek, ısıl genleşme oranı ise düşük olur.
Birarada bulunan atomlar, dış kabuğundaki valans elektronları etkileşerek daha düşük enerjili,
dolayısıyla daha kararlı bir yapıya sahip olma eğilimi gösterirler ve bu etkileşim sonucunda
atomlararası bağ kuvvetleri doğar.
Atomlararası bağ kuvvetleri zıt elektriksel yüklü parçacıklar arası elektrostatik veya Coulomb çekme
kuvvetlerinden kaynaklanır.
Öğle ki, atomlar birbirlerine elektron vererek, alarak yada elektron paylaşarak elektriksel yüklü hale
gelirler, işte bu durumda aralarında Coulomb çekme kuvvetleri doğar.
Atomlar bireysel halde belirli bir potansiyel enerjiye sahiptir. Aralarında bağlar oluşurken potansiyel
enerji azalır ve denge halinde minimuma erişir, bu durumda karalı yapı meydana gelir.
Atomlararası bağlar iki türdür;
1. Kuvvetli Bağlar
2. Zayıf Bağlar
Kuvvetli bağlar genellikle atomlararası elektron alışverişi veya elektron paylaşılması, zayıf bağlar ise
atomlar veya moleküller içerisinde elektronların asimetrik dağılışından kaynaklanan elektriksel
kutuplaşma sonucu oluşur. Her ikisinde de elektrostatik çekme kuvvetleri etkili olur. Ancak büyüklükleri
dolayısıyla enerjileri çok farklıdır. Zayıf bağları koparmak için gerekli ortalama enerji, kuvvetli bağalara
kıyasla yaklaşık 10 kat daha küçüktür.
Atomlararası Kuvvetli Bağlar (primer veya birincil bağlar) üç gruba ayrılır;
1.1. İyonik Bağlar
1.2. Kovalent Bağlar
1.3. Metalik Bağlar
3
MALZEME BİLİMİ
Giriş, Atomik Yapı
1.1. İyonik Bağlar; genellikle metalik elementler ile metalik olmayan (ametal) elementler arasında
valans elektronlarının alışverişinden kaynaklanan iyonlaşma sonucu oluşur. Elektron alan element
eksi yüklü iyon (anyon), veren element ise artı yüklü iyon (katyon) olur. Zıt yüklü bu atomlar arasında
elektrostatik Coulomb çekme kuvvetleri nedeniyle iyonik bağlar oluşur.
İyonik bağlar küresel nitelikli olup, üç boyutta etkilidir ve yönsüz bağlar olarak nitelendirilir.
Bir iyon çevresizdeki zıt yüklü iyonları kendine çeker, denge halinde potansiyel enerji minimum olur,
dolayısıyla kararlı yapı meydana gelir. Ancak kütle içinde artı yük sayısı eksi yük sayısına eşit olması,
diğer bir değişle net elektriksel yükün sıfır olması kararlı yapı için zorunludur.
Genellikle artı yüklü iyonlarla eksi yüklü iyonlar üç boyutlu uzayda ardışık dizilerek düzenli bir yapı
oluşturma eğilimi gösterirler. Bu nedenle NaCl, MgO, CaO ve Al2O3 gibi arı iyonik bağlı cisimler
çoğunlukla düzenli kristal yapıya sahiptirler.
Sodyum klorürde (NaCl) iyonik yapı oluşumu;
1.2. Kovalent Bağlar; ametaller ile ametaller arasında olup, genellikle gazlarda meydana gelir (H2,
NH3, O2, CH4). Bu bağ türünde Valans elektronlarının ortak kullanımı söz konusudur. Periyodik tabloda
birbirlerine yakın ve elektronegatiflikleri arasında az fark bulunan elemanların atomları veya aynı
elemanın kendi atomları valans elektronlarını çiftler halinde paylaşabilirler. Paylaşılan eksi yüklü
elektronlar artı yüklü iki komşu arasında sürekli titreşim halinde kalarak bir köprü oluştururlar. Bu
şekilde kovalan bağ oluşurken atomlar birbirlerine yaklaşır, potansiyel enerji azalarak minimuma erişir
ve kararlı bir yapı elde edilir.
Kovalent bağlar aynı tür atomlar arasında oluşabildiği gibi (H2, F2, O2), farklı tür atomlar arasında da
oluşabilir (H2O, CH4, CCl4). Bir atom valans kabuğunda her boş enerji düzeyine karşı bir çift elektron
alarak bir kovalent bağa sahip olur.
4
MALZEME BİLİMİ
Giriş, Atomik Yapı
Farklı ve aynı tür atomlar arasında Valans elektronlarının ortak kullanımı ile Kovalent bağ oluşumu:
1.3. Metalik Bağlar ise; valans enerji kabuğunda az sayıda
elektron (≤3) içeren atomlar arasında oluşur. Metaller son
yörüngelerindeki valans elektronlarını serbest bırakarak iyon
haline gelirler. Serbest kalan elektronların metal çekirdeği ile
bağları çok zayıftır ve hiçbir atoma bağlı kalmadan metal
çekirdekleri etrafında serbestçe dolaşırlar. Metal atomları
birbirine yaklaştığında son yörüngelerindeki enerji bantları
birbirinin içine girer ve serbest elektronlar bu bantlarda hareket
edebilirler. Metallerin valans elektronlarını serbest bırakmaları
özelliği, iyi elektrik iletimi sağlamalarına sebep olur. Bu bantlar içinde hareket eden negatif yüklü
elektronlar ile pozitif yüklü çekirdek arasındaki elektrostatik çekim kuvvetleri metalik bağı oluşturur.
Atomlararası Zayıf Bağlar (sekonder veya ikincil bağlar);
Atomlar veya moleküller içinde elektronlar asimetrik
dağılırsa artı ve eksi elektriksel yük merkezleri
çakışmaz, bunun sonucu elektriksel kutuplaşma
meydana gelir (dipol oluşumu), Zayıf bağlar diğer
bir deyimle Van der Waals kuvvetleri zıt işaretli iki
kutup
arasındaki
çekme
kuvvetlerinden
kaynaklanır.
MALZEMELERİN SINIFLANDIRILMASI
Endüstride çok çeşitli malzeme türleri vardır, ayrıca gün geçtikçe bunlara yenileri eklenmektedir.
Bunları ayrı ayrı ele alarak incelemek imkânsızdır. Bunun yerine yapı ve özellikleri benzer olanları
sınıflara ayırarak ortak yanlarını tanıtmak daha uygundur.
Eski kaynaklarda değişik sınıflandırmalara rastlanır. Ancak yakın yıllarda malzeme bilimindeki önemli
gelişmelerden yararlanarak ileri sürülen en tutarlı ve en uygun sınıflandırma atomlararası bağ türlerine
dayanır. Buna göre malzemeler;
1. METALİK MALZEMELER,
2. SERAMİK MALZEMELER ve
3. PLASTİK MALZEMELER (Polimerler) olmak üzere 3 sınıfa ayrılır.
5
MALZEME BİLİMİ
Giriş, Atomik Yapı
1. METALİK MALZEMELER; Metalik bağa sahip metallerde aynı veya benzer tür atomlar düzenli bir
biçimde dizilerek kristal yapı oluştururlar. Çelik, alüminyum, magnezyum, çinko, dökme demir,
titanyum, bakır gibi malzemelerdir.
Metalik malzemelerin karakteristik özellikleri,
Hacimsel atom yoğunlukları yüksektir,
Bu nedenle özgüI ağırlıkları diğer sınıflara göre büyüktür, çoğunlukla 7 Mg/m3’ün üstündedir.
Metaller serbest elektron içerdiklerinden ısıl ve elektriksel iletkenlikleri yüksektir.
Saydam olmayıp opaktırlar, ışığı iyi yansıtırlar,
Metallerin mukavemetleri ve elastisite modülleri yüksektir.
Çoğunlukla sünektirler ve plastik şekil vermeye elverişlidirler.
Ayrıca alaşımlandırma, soğuk şekil verme ve ısıl işlemle sertlik ve mukavemetleri artırılabilir.
2. SERAMİK MALZEMELER; metal ve metal olmayan elementlerin aralarında oluşturduğu iyonik
bileşiklerdir. Elektropozitif elementler (Na, Mg, Fe ve Al) elektronegatif elementlerle (Cl ve O) kolayca
iyonik bağlar kurarak NaCl, FeO, SiO2 ve MgO gibi çok çeşitli türde seramik malzemeler meydana
getirirler.
Beton, taş, tuğla, cam ve kiremit gibi seramik türden malzemeler, yapı üretiminde yaygın olarak
kullanılan yapı malzemeleridir.
Ayrıca ileri teknoloji seramik diye adlandırılan oksitler, karbürler ve nitrürler üstün mekanik
özelliklerinden dolayı son yıllarda büyük önem kazanmıştır.
Seramik malzemelerin karakteristik özellikleri,
Doğada çoğunlukla kristalli ve kısmen amorf yapıda bulunurlar.
Özgül ağırlıkları metallerden az, plastik malzemelerden çok olup 2 – 3 Mg/m3 arasındadır.
Seramikler plastik şekil değiştirmezler, sert ve gevrek olurlar.
Yüksek sertlikleri dolayısıyla (Al2O3 gibi), aşındırıcı (abrazif) olarak kullanıma elverişlidirler.
Ergime sıcaklıkları yüksektir.
Elektriksel iletkenlikleri düşüktür. Elektrikli ısıtıcılarda yalıtım malzemesi (refrakter malzeme) ve
elektrik hatlarında elektrik izolatör malzemesi olarak kullanılırlar.
Yüksek sıcaklık ve korozyonlu ortamlara dayanıklılıkları mükemmeldir.
Saydamdırlar, ışığı kötü yansıtırlar. Çekme mukavemetleri düşük olmakla beraber,
Basınç mukavemetleri yüksek ve dış etkilere dayanıklılıkları iyidir.
3. PLASTİK MALZEMELER (Polimerler); genellikle metal olmayan elementlerden oluşan kovalent
bağlı malzemelerdir. Ana element C (karbon) olup, bunun yanında çoğunlukla H (hidrojen), bazılarında
ise Cl, F, O, N ve S bulunabilir.
Monomer denilen molekül bireyleri birbirine kovalent bağlarla eklenerek çok büyük dev moleküllere
dönüştürülür ve dolayısıyla polimer adını alırlar.
Bu tür malzemeler üretiminin belirli aşamasında yumuşayarak plastik kıvam aldıktan ve sonra bir
kalıba enjekte edilerek şekil verilebildiklerinden plastik olarak anılırlar.
6
MALZEME BİLİMİ
Giriş, Atomik Yapı
Plastikler kovalent bağın sürekliliği ve atomların dizili biçimine göre iki faklı tür molekül yapısına
sahiptirler;
3.1. Lineer Polimerler (Termoplastikler)
3.2. Uzay Ağı Polimerleri (Termoset Plastikler)
3.1. Lineer Polimerler, kovalent bağlarla bir boyutta zincir şeklinde dizilirler, moleküller arası bağlar
zayıf türdendir. Isıtılınca bu zayıf bağlar koptuğundan kolayca yumuşarlar, soğuyunca sertleşerek
tekrar kullanılabilirler.
Polietilen (PET), polivinilklorür (PVC) ve polistren (EPS, XPS) gibi malzemeler örnek gösterilebilir.
3.2. Uzay Ağı Polimerleri ise, üç veya daha fazla reaksiyon bağına sahip merler üç boyutlu uzayda
sürekli kovalent bağ ağı oluştururlar. Bu tür polimerler üretim sürecinde sertleştikten sonra ısıtılma ile
yumuşamazlar, aşırı sıcaklıkta kovalent bağlar koparak parçalanır, dolayısıyla tekrar kullanılmaları söz
konusu değildir.
Bakalit, epoksi ve poliyester gibi malzemeler örnek gösterilebilir.
7
MALZEME BİLİMİ
Giriş, Atomik Yapı
Plastik malzemelerin karakteristik özellikleri,
Hacimsel atom yoğunlukları küçüktür, bu nedenle özgül ağırlığı düşük ve hafif malzemelerdir.
Polimerlerin ısıl ve elektriksel iletkenlikleri çok düşüktür, yalıtım malzemesi olarak kullanıma
elverişlidirler.
Arı halde genellikle saydamdırlar, ışığı geçirirler, bununla beraber en kötü yansıtıcıdırlar.
Mukavemetleri ve elastisite modülleri düşüktür.
Lineer polimerler yumuşak ve sünek olup kolay şekil değiştirirler,
Uzay ağı polimerleri ise sert ve gevrektir, plastik şekil değiştirmezler.
8
MALZEME BİLİMİ
Kristal Yapılar, Miller İndisleri
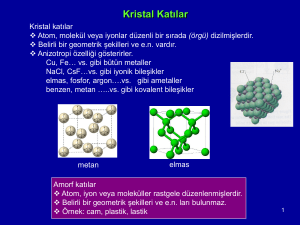
KRİSTAL YAPILAR
Malzemelerin içyapısı, atomlararası bağ kuvvetleri etkisinde atomların diziliş biçimine bağlıdır.
Atomların dizilişi düzenli ise KRİSTAL YAPI, düzensiz ve rastgele ise AMORF YAPI oluşur.
Düzenli yani kristal yapılı bir malzemede herhangi bir doğrultu boyunca atomlararası uzaklıklar eşit ve
çevreleri özdeştir.
Metallerin tümü, seramiklerin önemli bir kısmı ve bazı polimerler kısmen kristal yapılıdır.
Sıvı halde rastgele dağılmış olan atomlar katılaşırken düzenli biçimde dizilerek kristal yapıyı
oluştururlar. Ancak gerçekte kristal malzemelerin atomik yapılarında bazı içyapı kusurları da bulunur.
Bu bölümde öncelikle kusursuz kristallerin yapısı ve geometrik özellikleri ele alınacak, daha sonra
doğada bulunan gerçek kristallerin içerdikleri kusurlar tanıtılacaktır.
1. KRİSTAL YAPI VE TÜRLERİ
1832 yılında bir İngiliz mineralog olan William Hallowes Miller minerallerini incelerken, kristal yapıların
belirli bir oryantasyonda olduğunu ve belirli bir ufacık yapının sürekli tekrar ederek maddeleri
oluşturduğunu fark etmiştir. Bu en küçük tekrarlayan düzenli yapı birimine Birim Hücre denmiştir.
9
MALZEME BİLİMİ
Kristal Yapılar, Miller İndisleri
Kristal yapı, koordinat sisteminde eksenlere paralel düzlemler ile uzayın eşit hacimlere bölündüğü
basit bir geometrik şekille modellenirse, eş hacimlerden her biri de birim hücreyi temsil eder.
Genel koordinat sisteminde kristal yapı modeli ve birim hücre
Geometrik bir kural olarak, uzayı 7 farklı şekilde eşit hacimlere bölebiliriz. Gerçekten de doğada 7
farklı kristal türü veya kristal sistemi vardır.
Koordinat sisteminden görüldüğü gibi; x, y, z eksen takımlarını kesen düzlemlerin ayırdığı eşit
hacimlerden her biri eğik genel prizmalar şeklindedir. Birim hücre olarak adlandırılan bir prizmanın
açılarına ve kenarlarına özel değerler verilerek aşağıdaki 7 kristal sistemin ve türünün birim hücreleri
elde edilir.
Kristal Türleri
10
MALZEME BİLİMİ
Kristal Yapılar, Miller İndisleri
Kristal Türleri
11
MALZEME BİLİMİ
Kristal Yapılar, Miller İndisleri
Metallerin büyük çoğunluğu kübik kristal, yalnız Zn ve Mg hegzagonal kristal yapıya sahiptir. Diğer
kristal türlerine endüstriyel metallerde rastlanmadığından burada ele alınmayacaktır.
Ancak, birim hücrelerin biçimi içyapıyı tanıtmaya yetmez, ayrıca atomların diziliş biçimini içeren kafes
yapıları da bilmek gerekir.
2. KAFES YAPILAR
Atomların kristal sistemindeki diziliş biçimi Kafes Yapı olarak adlandırılır. Belirli bir kristal türüne
atomları birden fazla biçimde dizme olanağı vardır. Yedi kristal türü için toplam 14 farklı kafes yapı
(atomsal diziliş) olasılığı vardır. Burada yalnız kübik kafes yapılar ele alınacaktır.
2.1. Kübik Kafes Yapılar
Geometrik yönden kübik kristale atomlar 3 ayrı şekilde dizilerek içyapıyı oluşturur.
1. Basit Kübik (BK) Kafes
2. Hacim Merkezli Kübik (HMK) Kafes
3. Yüzey Merkezli Kübik (YMK) Kafes
2.1.1. Basit Kübik (BK) Kafes
Basit kübik kafes yapıda, küpün her köşesinde bir atom bulunur ancak kararsız bir diziliş türü
olduğundan doğada bu yapıya sahip bir element yoktur.
12
MALZEME BİLİMİ
Kristal Yapılar, Miller İndisleri
2.1.2. Hacim Merkezli Kübik (HMK) Kafes
Küpün her köşesinde birer atom ve merkezinde de bir atom bulunur ve köşe atomları merkez atoma
teğettir. Atomun yarıçapı R olduğuna göre birim hücrenin kenarı a’nın R cinsinden ifadesi, 4R/√3 tür.
Gerçekte her köşedeki atom 8 komşu birim birim hücre arasında paylaşılmaktadır. Küpün merkezinde
bulunan 1 atom ve her bir köşede bulunan 1/8 atomla birlikte birim hücredeki toplam atom sayısı 2 dir.
Hacim merkezli kübik (HMK) kafes
Birim hücredeki atomların diziliş sıklığını ifade etmek için Atomsal Dolgu Faktörü (ADF) kullanılır. Buna
göre (HMK) kafesin atomsal dolgu faktörü;
Bu sonuca göre hacim merkezli kübik kafese sahip bir yapıda hacmin %68’i dolu, %32’si boştur.
2.1.3. Yüzey Merkezli Kübik (YMK) Kafes
Yüzey merkezli kübik kafeste, birim hücrenin köşelerinde birer ve yüzeylerin merkezinde de birer atom
vardır. Birim hücrede, biri köşelerde üçü yüzey merkezlerinde olmak üzere toplam 4 atom vardır. Birim
hücrenin bir kenarı bir kenarı a’nın R cinsinden ifadesi, 4R/√2 tür.
13
MALZEME BİLİMİ
Kristal Yapılar, Miller İndisleri
(YMK) kafesin atomsal dolgu faktörü;
Metaller çoğunlukla YMK kristal yapıya sahiptir. Ayrıca iyonik bileşiklerin önemli bir kısmı da YMK
kristal yapılıdır. Şekilde birim hücresi görülen NaCl bunlara bir örnektir.
2.2. Hegzagonal Kafes Yapılar
Hegzagonal sık düzen kafesinin (HSD) birim hücresinde; köşelerde 12x1/6= 2, alt ve üst tabanda
2x1/2 = 1 ve içinde de 3 olmak üzere birim hücrede toplam 6 atom bulunur.
Hegzagonal sık düzenin (HSD) atomsal dolgu faktörü hesaplanırsa 0,74 olup (YMK) ile aynıdır.
Doğada bu tür kafes yapıya sahip element bulunmamaktadır.
3. POLİMORFİZM (Allotropizm)
14
MALZEME BİLİMİ
Kristal Yapılar, Miller İndisleri
Aynı bileşimde iki molekül değişik atomsal dizilişe sahipse bunlara İZOMER denir.
Buna benzer şekilde aynı kimyasal bileşime sahip fakat değişik kristal yapılı cisimlere polimorflar ve bu
özelliğe de POLİMORFİZM denir.
Bunun en ilginç örneği demirdir. Demir oda sıcaklığında (HMK) 910 oC’nin üstünde (YMK) 1400 oC’nin
üstünde de (HMK) kristal yapılıdır.
Yüksek sıcaklıkta sık dizili YMK yapılı demir, soğurken seyrek dizili HMK yapılı demire dönüşürken
hacmi artar.
Bu özelliğe sahip malzemelerin hangi kristal yapıda bulunduğu, sıcaklığa ve dış basınca bağlıdır.
4. KRİSTAL GEOMETRİSİ
Kristallerde atomların merkezlerini birleştiren doğrular uzatılarak uzayda
kafes görünümünde bir yapı elde edilir, bundan dolayı buna kafes yapı
denilmektedir.
Değişik doğrultularda ve değişik düzlemlerde aynı atomsal diziliş
görülebileceği gibi farklı atomsal dizilişler de görülebilir. Bu nedenle,
malzeme özellikleri de değişik düzlemlere ve doğrultulara göre farklılık
gösterebilir.
Malzemelerin tüm özelliklerinin doğrultudan bağımsız olması özelliği İzotropi, özelliklerin doğrultuya
bağlı olarak değişiklik göstermesi özelliği ise Anizotropi olarak tanımlanır.
Çelik izotrop malzemelere, ahşap ise anizotrop malzemelere örnek gösterilebilir.
Nitekim kristal yapılı malzemelerin özelliklerini ortaya koymak için içyapılarını geometrik yönden de
incelemek ve kristal doğrultularını belirlemek gerekir.
4.1. Kristal Doğrultuları
Kristallerin birçok özelliği kristal doğrultularına
bağlı olarak değişir. Kristal doğrultularını
belirtmek için Miller İndisleri kullanılır.
Bir kafes yapıda herhangi bir doğrultuya paralel
sonsuz sayıda doğru vardır. Kristal yapıyı
tanıtmak için ana doğrultulara paralel bir o-xyz
eksen takımı seçilir. Miller indisleri, belirlenecek
doğrultuya paralel olup, orijinden başlayarak bir
sonraki kafes köşesinde sona eren doğrultu
vektörü tanımlanır. Bu doğrultu vektörünün
eksenler üzerindeki izdüşümleri, kafes sabiti
cinsinden, [hkl] şeklinde ifade edilen en küçük
tam sayılar dizisi o doğrultunun Miller indisleridir.
15
MALZEME BİLİMİ
Kristal Yapılar, Miller İndisleri
Örneğin şekilde görüldüğü gibi; ox doğrultusunun (1) doğrultu vektörünün bu eksen üzerindeki bileşeni
a, diğerleri üzerindeki bileşenleri sıfırdır. Bu bileşenler a kafes sabitine bölünür ve bulunan 1,0,0
boyutsuz tam sayıları, bu doğrultunun miller indisleri olarak [100] şeklinde ifade edilir.
4.2. Kristal Düzlemleri
Kristallerde atomlar düzlemler üzerinde dizilirler. Atomların diziliş biçimi ve diziliş sıklığı, üzerlerinde
bulundukları düzlemlere göre değişir, dolayısıyla özellikler de kristal düzlemlerine bağlı olarak değişir.
Kafes yapıdaki belirli bir düzlemi belirtmek için (hkl) şeklinde tam sayılardan oluşan Miller indisleri
kullanılır.
Şekilde verilen düzlem xyz eksenlerini orijinden
başlayarak a, 2a ve a mesafelerinde kesmektedir.
Bu doğru kesitleri, kafes sabiti a’ya göre boyutsuz
hale getirilir; 1,2,1. Sonra bu sayıların tersleri alınır;
1/1, 1/2, 1/1. Bu sayılar uygun bir ortak çarpanla
çarpılarak en küçük tam sayılar grubu elde edilir;
2x(1,1/2,1)=2,1,2. Bunlar bu düzlemin Miller indisleri
olup tırnak içinde virgül koymadan verilir; (212).
16
MALZEME BİLİMİ
Kristal Kusurları, Atomsal Yayınım
KRİSTAL YAPI KUSURLARI
Önceki bölümlerde kusursuz kristallerin yapısı tanıtıldı. Bu yapılırken genellikle küp veya prizma
şeklinde tek kristaller ele alındı ve kristal içinde bütün kafes köşelerinin aynı tür atomlar (arı metal)
tarafından doldurulduğu, bütün kristal düzlemlerinin ve doğrultularının kristal boyunca uzandığı
varsayıldı.
Ancak gerçekte kusursuz kristal yok sayılır. Kristallerin içinde değişik boyutta yabancı atomlar
bulunabilir, bazı kafes köşeleri boş (eksik atom), bazı atomlar yerinden kaymış ve bazı kristal
düzlemleri yarım olabilir. Bunlardan başka cisim tek yerine çok kristalden oluşabilir.
Yukarıda sözü edilen tüm etkenler ve çok kristalli cisimlerde sınır bölgeleri kütlenin düzenli yapısını
bozar ve kusurlu hale getirir. Bu kusurların biçimi, boyutu ve miktarı toplam kütleye göre çok az olsa
da özellikleri büyük ölçüde etkiler. Malzemelerin gerçek davranışını açıklayabilmek için bu kusurları
yakından tanımak gerekir.
Bu bölümde yalnız arı kristallerdeki kusurlar ele alınacak, yabancı atomların neden olduğu içyapı
kusurlarını içeren gerçek malzemelerin davranışı ise ayrı bir bölümde tanıtılacaktır.
Kristal kusurları üç çeşittir;
1. NOKTASAL Kusurlar
2. ÇİZGİSEL Kusurlar (Dislokasyonlar)
3. DÜZLEMSEL Kusurlar
Noktasal Kusurlar; birkaç eksik veya yer değiştirmiş atomdan kaynaklanır. Bunların mekanik
özelliklere etkisi önemsizdir.
Çizgisel Kusurlar; kristalde boydan boya bir çizgi boyunca uzanan şekildeki kusurlardır. Bu tür kusur
özellikle metallerin mekanik özelliklerini büyük ölçüde etkiler.
Yüzeysel Kusurlar; iki boyutlu olup, kristallerin yüzeyleri ve çok kristalli yapılarda kristal bireyleri
arasındaki tane sınırlarıdır.
1. NOKTASAL Kusurlar
Bir atomun eksik olduğu boş kafes köşesidir ve simgesi ile belirtilir.
Noktasal kusurların oluşum nedenleri;
Sıvı metal katılaşırken, plastik şekil değiştirme ve yüksek sıcaklıkta ısıl titreşim gibi etkilerle
atomların yer değiştirmesi
Kafes yapıda atomlar arası yeterli boşluk varsa araya giren fazla atom (arayer atomu)
Kafes köşesinde bulunan farklı büyüklükteki atomlar
Noktasal kusurlar çevrelerinde gerilme alanı yaratırlar. Mekanik özelliklere etkileri az, elektriksel
özelliklere etkileri büyüktür.
17
MALZEME BİLİMİ
Kristal Kusurları, Atomsal Yayınım
Noktasal kusur nedenleri ve türleri;
2. ÇİZGİSEL Kusurlar (Dislokasyon)
Çizgisel kusurlar kristallerde atomsal dizilişin bir çizgi boyunca bozulması sonucu oluşur. Atomlar
denge konumundan ayrıldıklarından çizgi çevresinde artık gerilmeler doğar.
Dislokasyonlar çoğunlukla katılaşma sürecinde oluşmakla beraber plastik şekildeğiştirme sırasında
sayıları artar.
Kenar Dislokasyonu ve Vida Dislokasyonu olmak üzere başlıca iki tür basit dislokasyon vardır.
18
MALZEME BİLİMİ
Kristal Kusurları, Atomsal Yayınım
2.a) Kenar Dislokasyonu
Kenar dislokasyonu kristal yapıda kısmen eksik bir atom düzleminin kenarı olarak tanımlanır. Kenar
dislokasyonları ┴ simgesi ile belirtilir.
Düzlemin ucundaki atomlar sıkışık durumda olup basınç bölgesi, altındakiler de açılmaya
zorlandıklarında çekme bölgesi meydana gelir.
Aşağıda, kuvvet etkisiyle bir kenar dislokasyonun ilerleyişi sembolik olarak gösterilmiştir.
2.b) Vida Dislokasyonu
Vida dislokasyonu kristalde bir düzlem boyunca kısmen kayma şeklinde ötelenme sonucu oluşur.
Şekilde görüldüğü gibi; kristalin ön üst kısmı, alt kısmına göre bir atom mesafesi büyüklüğünde sağa
doğru kaymıştır. Göreli olarak kayan (renkli) yüzeylerin sınırındaki kırmızıçizgi Dislokasyon Çizgisi
olarak isimlendirilir ve hareket dolayısıyla bu çizgi boyunca kayma gerilmeleri doğar, dolayısıyla
potansiyel enerji artar.
Vida dislokasyonu ismini, atom düzlemlerinin dislokasyon çizgisi etrafında spiral veya helisel bir yol
izlemesinden alır. Vida dislokasyonları U sembolü ile gösterilir.
Gerçekte kristallerde karışık türden dislokasyonlar vardır. Elektron mikroskobu ile elde edilen
görüntülerde dislokasyonların çok karışık ve sürekli uzay ağı şeklinde oldukları saptanmıştır.
19
MALZEME BİLİMİ
Kristal Kusurları, Atomsal Yayınım
3. DÜZLEMSEL Kusurlar (Yüzeyler ve Tane Sınırları)
Kristallerin yüzeyleri ile çok kristalIi yapılarda kristal bireyleri arasındaki tane sınırları iki boyutlu kusur
sayılırlar.
Yüzeyler:
Bir kristal bireyinin yüzeyinde bulunan atomlar içinde bulunan atomlarla eşdeğer değildir. Yüzey
atomlarının yalnız bir tarafında kusurları vardır. Bundan dolayı yüzey atomlarının enerjileri daha
yüksek ve içindekilere göre daha zayıf bağlıdırlar.
Tane Sınırları:
Kristal yapılı malzemeler sıvı halden katılaşırken aynı anda birçok kristal çekirdeği oluşmaya başlar ve
bunlar kütleyi doldururlar, sonuçta çok kristalli bir yapı elde edilir.
Çok kristalli bir malzemede kristal bireylerine TANE denir. Tanelerdeki kristal doğrultular rasgele
dağılmıştır. Şekilde görüldüğü gibi kristaller büyürken sıvı içindeki atomlar sürekli olarak kristallere
katılarak düzenli hale geçerler. Tanelerin biçimi ve büyüklüğü komşuları tarafından sınırlanır,
birbirlerine değdikleri yerde tanelerin büyümesi durur. Kristal bireyleri kalan atomlar komşu tanelerle
uyum sağlayamazlar, dolayısıyla rasgele düzensiz halde dağılmış durumda kalırlar. Taneler
arasındaki bu düzensiz amorf bölgeye TANE SINIRI denir.
Tane sınırları kimyasal etkilere karşı daha duyarlıdırlar. Atomsal yayınım daha kolay olur ve korozyon
daha hızlı ilerler. Diğer taraftan komşu tanelerle uyum sağlayamadıklarından dislokasyon
hareketlerine engel olurlar.
Nitekim bir metalde, taneler küçüldükçe tane sınırı alanı büyür, dolayısıyla engeller artar. Bunun
önemli bir sonucu olarak, plastik şekil değiştirme kısıtlanır ve mukavemet artar.
20
MALZEME BİLİMİ
Kristal Kusurları, Atomsal Yayınım
Metallerin içyapısını inceleyen bilim dalına metalografi denir. Metalin içyapısını incelemek için, önce
incelenecek metal numunenin yüzeyi parlatılır, sonra uygun bir ayıraç dağlanır. (Örneğin demir için %2
nitrik asit içeren etil alkol dağlama ayıracı olarak kullanılır.) Metalin yüzeyine pamukla sürülen ayıraç
tane sınırlarındaki atomları kolaylıkla eriterek uzaklaştırır ve böylece ağ şeklinde belirgin dağlama
çukurları oluşur. Metal mikroskobunda, tane sınırlarındaki çukurlara düşen ışık demeli dağılır ve bu
bölgeler koyu, tanelerin yüzeyi ayıraçtan daha az etkilendiğinden ışık yansıyarak geri döner,
dolaysıyla daha açık renkte görünür.
ATOM HAREKETLERİ VE ATOMSAL YAYINIM
Malzemelerin üretim ve uygulama süreçlerinde görülen katılaşma, çökelme, yeniden kristalleşme ve
tane büyümesi gibi olaylarla kaynak ve sementasyon gibi işlemler büyük ölçüde atomların kütle
içindeki hareketlerine bağlı olarak meydana gelir.
Isıl enerji etkisinde oluşan bu hareketler iki farklı aşamada gerçekleşir.
İlki; ısıl etki ile atomların kendi denge konumları çevresindeki küçük titreşim hareketleri,
İkincisi ise; yine ısıl etki ile bir denge konumundan diğerine atlayarak yaptıkları uzak mesafe
hareketleridir. Bu ikinci davranış Atomsal Yayınım veya Difüzyon olarak adlandırılır.
Atomsal yayınım sonucu cismin yapısı ve bunun sonucu olarak da özellikleri değişir. Katı
malzemelerde meydana gelen difüzyon gaz ve sıvılardaki difüzyondan çok daha yavaştır.
21
MALZEME BİLİMİ
Kristal Kusurları, Atomsal Yayınım
1. ATOMSAL YAYINIM MEKANİZMALARI
Sıcaklık yükseldikçe atomların ısıl titreşimleri artar ve bir kısmı içinde bulunduğu yapıda bir konumdan
diğer konuma atlayarak yer değiştirir. Atomsal yayınım veya difüzyon denen bu olayda, önce atomun
çevresi ile bağları kopar, sonra atomlararası boşluklardan geçer ve yeni konumunda çevresi ile yeni
bağlar kurar.
Kütle içinde atomların yayınımı üç farklı şekilde gerçekleşebilir;
1.1. Boşluk Yayınımı: bir atomun yanındaki boşluğu doldurmak için kendi kafesindeki yerini terk
etmesidir (bu nedenle orijinal kafes yerinde yeni bir boşluk oluşturur).
Boşluk
2. Durum
1. Durum
1.2. Arayer Yayınımı: kristal yapıda mevcut bulunan küçük bir arayer atomunun bir arayerden
diğer bir arayere hareketidir. Bu mekanizmanın gerçekleşmesi için boşluklara gerek yoktur.
Arayer
Atomu
Arayer
1. Durum
2. Durum
1.3. Halka Yayınımı: olasılığı düşük olmakla beraber, birbirine değen atomlar aynı anda ve aynı
yönde hareket ederek birbirlerinin yerini alabilirler. Bu tür yayınım çok büyük enerji
gerektirdiğinden ancak ergime sıcaklığına yakın bölgelerde oluşabilir.
Yayınımların çoğu boşluk ve arayer mekanizmalarıyla gerçekleşir.
22
MALZEME BİLİMİ
Kristal Kusurları, Atomsal Yayınım
2. YAYINIM İÇİN AKTİVASYON ENERJİSİ
Atomlar, mutlak sıfır sıcaklıkta (0 oK) statik haldedir ve potansiyel enerjileri minimumdur. Isıl enerji
vererek sıcaklık arttırıldığı zaman atomlar kendi denge konumları çevresinde titreşmeye başlarlar,
aralarındaki bağıl uzaklık sürekli değişir ve dolayısıyla sahip oldukları kinetik ve potansiyel enerjiler de
değişir.
Katı yapı içinde yeterli düzeyde yüksek enerjiye sahip atomlar bir denge konumundan diğerine
atlayarak atomsal yayınımı oluştururlar. Hareket eden bir atom yeni yerine ulaşmak için çevre
atomların sıkıştırma engelini geçmek zorundadır. Bu enerji engelini aşmak için atoma enerji
sağlanmalıdır. Bunun için atom ısıtılır.
Yayınan bir atomun bir enerji engelini aşması için gerekli enerjiye Aktivasyon Enerjisi (Q, kal/mol)
denir. Yayınımın oluşabilmesi için aktivasyon enerjisi enerji engeline eşit olmalıdır.
Genellikle yeralan atomların yayınımı için arayer atomlarından daha fazla aktivasyon enerjisine ihtiyaç
vardır.
3. ATOMSAL YAYINIM KURALLARI
Bir yayınım sistemi genellikle bir anafaz (eriten sistem) ile o fazın yapısında hareket eden yabancı
atomlardan (eriyen sistem) oluşur.
Şekilde, Ni kaplanmış Cu kristali görülmektedir. Başlangıçtaki yüzeyde bütün atomlar Ni ‘dir. Yüksek
sıcaklıkta yeterince uzun beklenirse bakır ve nikel atomları bütün metal boyunca düzenli olarak dağılır.
23
MALZEME BİLİMİ
Kristal Kusurları, Atomsal Yayınım
3.1. Yayınım Hızı (1. Fick Kanunu)
Bir malzeme içinde atomların yayınım hızı, birim zamanda birim düzlem alanı boyunca geçen atom
sayısı olarak tanımlanan akı “J” ile ölçülebilir. 1. Fick kanunu net atom akısını açıklar.
J
Atomsal yayınım akısı (atom/(m2s))
D
Yayınım katsayısı (m2/s)
c
Atom konsantrasyonu
Δc / Δx
Konsantrasyon gradyanı
Konsantrasyon gradyanı yüksek iken başlangıçtaki akısı da yüksektir ve gradyan azalırken düzenli bir
şekilde düşer. Yayınım katsayısı sıcaklığa, yayınım sisteminin türüne ve yapısına bağlıdır. Yayınım
olayı hacim yayınımı, yüzey yayınımı ve tane sınırı yayınımı olmak üzere üç çeşittir.
D
Yayınım katsayısı (m2/s)
Q
Aktivasyon enerjisi (kal/mol),
R
Gaz sabiti (8,314 J / molK)
T
Mutlak sıcaklık
D0ve Q yayınım sistemine bağlı sabitler olup deneysel yolla ölçülebilirler.
Bazı metallerde yayınım sabiti ve aktivasyon enerjisi
24
MALZEME BİLİMİ
Kristal Kusurları, Atomsal Yayınım
Küçük atomlar daha kolay yayınır.
Belirli bir atom ergime sıcaklığı düşük dolayısıyla atomlararası bağ daha zayıf olan ortamda daha
kolay yayınır.
Atomsal dolgu faktörü düşük ortamlarda yayınım daha az enerjiyi gerektirir.
Düzensiz yapıya sahip ve atom sıklığı tanelere göre daha az olan tane sınırları boyunca yayınım
daha kolay oluşur. Bu nedenle faz dönüşümleri ve korozyon olayları tane sınırlarında başlar ve
daha hızlı oluşur.
3.2. Kompozisyon Profili (İkinci Fick Kanunu)
İkinci Fick kanunu ise, atomların dinamik veya durağan olmayan hallerini tanımlar.
Şeklinde bir diferansiyel eşitliktir. Denklemin çözümü belirli bir durum için sınır
kurallarına bağlıdır.
D terimi sabit kaldıkça değişik şartlarda aynı konsantrasyon profili elde edilebilir. Bu özellik, belirli bir
ısıl işlemin uygulanması için gerekli zaman üzerine sıcaklığın etkisini belirlemeyi sağlar.
4. ATOMSAL YAYINIMIN OLUŞTUĞU BAZI ENDÜSTRİYEL UYGULAMALAR
4.1. Sementasyon İşlemi
Az karbonlu çelik yumuşak ve sünektir, işlenmesi kolaydır. Ancak aşınma mukavemeti düşüktür.
Çeliğe şekil verdikten sonra sürtünmeye maruz kalacak yüzeylere sementasyon işlemi uygulayarak
yüzeysel karbon oranı artırılır, sonra su vererek sertleştirilir, böylece aşınmaya daha dayanıklı olur.
Sementasyon işleminde az karbonlu çelik aktif karbon atomları içeren bir ortamda yüksek sıcaklıkta
(800 oC’ın üzerinde) ısıtılır. Karbon atomlarının yayınması sonucu yüzeyde ince bir tabaka boyunca
yüksek karbonlu bir yapı oluşur. Bu şekilde semente esilmiş çeliğe su verilirse yüzeyi sert ve
aşınmaya dayanıklı içi yumuşak ve tok bir malzeme (motorların krank mili için uygun) elde edilir.
4.2. Galvanizasyon İşlemi
Demirin korozyona karşı mukavemetini artırmak için ergimiş çinko banyosuna daldırılır. Çinko
yüzeysel yayınım sonucu demir yüzeyinde ince bir tabaka oluşturur. Bu şekilde elde edilen galvanizli
saçlarda ve borulardaki çinko tabakası ana metali korozyona karşı korur.
4.3. Kaynak ve Lehim İşlemi
Metal parçalarını birleştirmek için uygulanan bu işlemler yayınım olayı ile gerçekleşir. Kaynak
işleminde; iki metal parçası yüksek sıcaklıkta ergitilerek aralarında uzak mesafeli bir yayınım sağlanır.
Ergitme için gaz alevi veya elektrik arkı kullanılır. Yüksek sıcaklıkta basınç altında iki metal parçası
arasında yayınım sonucu kaynak oluşur. Buna basınç veya demirci kaynağı denir. Ergime sıcaklığı
1500 oC olan demire basınç kaynağı 800 oC civarında uygulanır. En iyi bileşim ergitme kaynağı ile
sağlanır ve kaynak bölgesinin mukavemeti ana metalden daha yüksektir.
25
MALZEME BİLİMİ
Kristal Kusurları, Atomsal Yayınım
Lehimde ise dolgu metalinin ergime sıcaklığı birleştirilecek ana metalinin çok altındadır. Dolgu
metalinin ergime sıcaklığı 400 oC’nin altında ise yumuşak lehim denir. Sert lehimde pirinç veya gümüş
alaşımları, yumuşak lehimde ise kurşun-kalay alaşımları kullanılır. Lehim metalinin ergime sıcaklığı
yükseldikçe yayınım derinliği artar ve daha mukavim bir birleşim sağlanır.
4.4. Sinterleme ve Toz Metalurjisi
Sinterleme
(pişirme)
;
malzeme
parçacıklarının birbirleriyle birleşmesini
sağlayan ve kademeli bir şekilde
parçacıklar arasındaki gözenek hacmini
azaltan bir yüksek sıcaklık işlemidir.
Sinterleme esnasında difüzyon işlemleri.
Temas noktalarında atomlar difüz eder,
körüler oluşturur ve sonunda boşlukları
doldurur.
İnşaat endüstrisinde dolgu duvar ve çatı örtü malzemesi olarak yaygın şekilde kullanılan tuğla ve
kiremitin üretim sürecinde, mukavemet kazandırmak için uygulanan pişirme işlemi, atomsal yayınımla
gerçekleşen sinterleme uygulamalarına iyi bir örnektir.
26
MALZEME BİLİMİ
Faz Dönüşümleri ve Faz Diyagramları
FAZ DÖNÜŞÜMLERİ VE FAZ (DENGE) DİYAGRAMLARI
Önceki bölümlerde cisimlerin içyapıları tanıtıldı. Bu bölümde ise içyapıların nasıl oluştuğu ve içyapı
oluşumunu hangi etkenlerin ne şekilde etkilediği ele alınmıştır.
Bir cisim, bağ kuvvetleri etkisi altında en düşük enerjili denge konumunda bulunan atomlar grubundan
oluşur. Homojen olarak dizilmiş bu atomlar kararlı denge halinde belirli bir faz meydana getirirler.
Ancak koşullar değişirse enerji içeriği değişir, denge bozulur, atomlar daha düşük enerji gerektiren
başka bir denge konumuna geçerek değişik biçimde dizilirler ve sonuçta yeni bir FAZ oluşur. Fazların
oluşumunda ve dönüşümünde ana etken enerji içeriğidir.
Enerji içeriğini değiştiren 3 ana etken;
Sıcaklık,
Basınç ve
Bileşim dir.
Arı cisimler tek bileşenli en basit yapılı sistemlerdir, sıcaklık ve basınca bağlı olarak KATI, SIVI ve
GAZ halinde bulunurlar. Birden fazla tür atom içeren çok bileşenli sistemlerin dengesi ise çok daha
karışıktır.
Bu değişkenler etkisinde oluşacak fazların türlerini ve bunların özelliklerini bilmek uygulama yönünden
çok önemlidir. Böylece amaca uygun özelliklere sahip malzeme üretimi olanakları sağlanabilir. Bunun
için gerekli bilgiler de ancak denge diyagramları yardımıyla elde edilebilir.
Denge diyagramları yardımı ile belirli bir malzeme sisteminde sıcaklık ve bileşime bağlı olarak
oluşacak fazların türleri, bileşimleri ve miktarları hatta içyapılar da tahmin edilebilir. Endüstride
malzeme üretiminde ve mekanik özellikleri değiştirmek için uygulanacak ısıl işlemlerde denge
diyagramlarından büyük ölçüde yararlanılır.
Fazların Dengesi
Cisimlerin içyapı oluşumunda en önemli ana etken enerjidir. Doğanın temel fiziksel özelliklerinden
birisi, enerjisi azalan bir cisimde kararlılığın artmasıdır. Cisimler iki tür enerjiye sahiptir;
Potansiyel enerji
Kinetik enerji
Potansiyel enerji iki kaynaktan doğar, birincisi yer çekimi, diğeri ise zıt işaretli elektriksel alanlar
arasındaki Coulomb çekme kuvvetidir.
Cisme verilen ısıI enerjinin bir kısmı ısıl genleşmeye sarf edilir, dolayısıyla potansiyel enerji artar.
Diğer önemli bir kısmı ise ısıl titreşimleri artırarak kinetik enerjiye dönüşür.
Cismin yaklaşık olarak ısı içeriği de diyebileceğimiz ENTALPİ (H), iki kısımdan oluşur, biri; serbest
enerji (F) ve diğeri; içyapı düzensizlik derecesine bağlı karışım enerjisi (TS) dir. Yani; [ H = F + TS ]
Serbest enerji (F), faz dönüşümlerinde kararlı denge yapısının oluşmasında önemli rol oynar. Daima
serbest enerjisi minimum olan yapılar kararlı olur.
0oK sıcaklığında atomlar statik haldedir ve entropi (bir atomik sistemin düzensizliğinin ölçüsü) sıfırdır,
entalpi (H) ise minimumdur ve serbest enerjiye eşittir. Entalpi sıcaklıkla sürekli artar, serbest enerji ise
sıcaklıkla sürekli azalır.
27
MALZEME BİLİMİ
Faz Dönüşümleri ve Faz Diyagramları
Örneğin, su buharlaşırken sıcaklık sabit kalır, verilen bütün ısıl enerji içyapı düzensizliğine sarfedilir ve
entalpisi artar. Buharlaşma noktasından sonraki serbest enerji değişimi (ΔF = Fbuhar – Fsu) görüldüğü
gibi ΔF<0 dır. Buradan 100°C’nin üstünde düşük serbest enerjili buhar fazının kararlı olacağı
sonucuna varılır.
Entalpi ve Serbest enerjinin
sıcaklıkla değişimi
Suyun serbest enerjisinin sıcaklıkla değişimi
Fazlar Kuralı
Bir sistemdeki fazların denge halinde bulunması için gerekli koşulları belirler. Fazların dengesini
etkileyen üç temel etken; bileşim, sıcaklık ve basınçtır. Laboratuvar deneyleri genellikle sabit
basınçta uygulandığından bileşim ve sıcaklık olmak üzere iki değişken vardır.
Bir malzeme sisteminde fazlar ve dönüşümleri bileşim ve sıcaklığa bağlı olarak değişir, bu değişmeler
denge veya faz diyagramları ile gösterilir.
F + D = B +1
B
Mevcut bileşenlerin sayısı
D
Değişken sayısı
F
Fazların sayısı
kkl
Soğuma Diyagramları
Denge diyagramlarını elde etmek için soğuma diyagramlarından yararlanılır. Birden fazla bileşenli
sistemlerde değişik bileşimde bir seri alaşım hazırlanarak ergitilir, sonra soğuma süresince sıcaklığın
zamanla değişimi ölçülür. Elde edilen sonuçlar sıcaklık-zaman eksenleri üzerinde işaretlenerek
soğuma eğrileri elde edilir.
28
MALZEME BİLİMİ
Faz Dönüşümleri ve Faz Diyagramları
Arı metallerde katılaşma süresinde sıcaklığın sabit kalma zorunluluğu fazlar kuralı ile kanıtlanır.
Eğrideki 2 noktasında sıvı ve katı olmak üzere iki faz vardır, dolayısıyla F=2 dir. Arı metal olduğundan
bir bileşenlidir ve B=1 dir. Bu değerler fazlar kuralı denklemine konursa; 2+D=1+1 gereğince bağımsız
değişken sayısı D=0 elde edilir. Bu sonuca göre; iki faz bir arada bulunduğu sürece bağımsız
değişken yoktur, yani sıcaklık sabit kalmak zorundadır.
Denge (Faz) Diyagramları
Bir malzeme sisteminde fazların bileşimine ve sıcaklığa bağlı olarak değişimini gösteren diyagramlara
Denge Diyagramları veya Faz Diyagramları denir.
Bu diyagramlar malzeme üretiminde, içyapıları ve kararlılık bölgelerini saptamada ve ayrıca çeşitli ısıl
işlemlerde kullanılır. Faz diyagramları soğuma diyagramları yardımı ile elde edilirler.
Katı
( Likidüs: sıvılık, Solidüs: katılık )
Denge diyagramlarının soğuma diyagramları yardımıyla elde edilişi
(Birbirini sınırsız oranda eriten [Cu-Ni] gibi iki bileşenli bir sistemin faz diyagramı)
29
MALZEME BİLİMİ
Faz Dönüşümleri ve Faz Diyagramları
Şekil (b) deki diyagramda düşey eksen sıcaklık, yatay eksen B atomlarının ağırlık yüzdesi cinsinden
bileşimi gösterir. TA; A metalinin ergime, TB ise; B metalinin ergime sıcaklıklarıdır. Bu şekilde bir
alaşım için elde edilen üst ve alt noktalar birleştirilirse bu sistemin faz diyagramı elde edilmiş olur.
Liküdüs denen üst eğrinin üstünde yalnız sıvı faz, Solidüs denen alt eğrinin altında da yalnız katı faz
ve bu ikisinin arasında da (sıvı+katı) faz bulunur.
Faz Diyagramlarının Çeşitleri
1. Sıvı halde sınırsız çözünen sistem
a) Katı halde sınırsız çözünen
b) Katı halde kısmen çözünen
c) Katı halde hiç çözünmeyen
2. Sıvı halde kısmen çözünen sistem
a) Katı halde kısmen çözünen
b) Katı halde hiç çözünmeyen
3. Sıvı halde hiç çözünme olmayan sistem
a) Katı halde hiç çözünme olmaz
Denge Diyagramlarından Elde Edilen Bilgiler
a) Fazların türü
Bir alaşım sisteminde verilen bir sıcaklıkta mevcut fazların türü sıvı, sıvı+katı veya katı şeklinde
belirlenebilir.
A ve B metallerinden oluşan bir sistemde bileşimi
%B0 olan bir alaşım, şekilde görüldüğü gibi;
(1) noktasında sıvı,
(2) noktasında sıvı ve katı ve
(3) noktasında da yalnız katı faz içerir.
CC
30
MALZEME BİLİMİ
Faz Dönüşümleri ve Faz Diyagramları
b) Fazların bileşimi
Tek fazlı bölgede, mevcut fazın bileşimi göz önüne alınan alaşımın bileşimine eşdeğerdir. Yani,
%B0’lık alaşımda, (1) noktasındaki sıvı faz %B0, (3) noktasında katı faz da %B0 bileşimindedir.
Bu sıcaklıklarda mevcut A atomlarının yüzdesi: %Ao = %100 - %B0 şeklinde belirlenebilir.
Ancak iki fazlı bölgede, fazların bileşimi alaşımın bileşiminden farklıdır. Bunu açıklamak için, %B0
oranında B içeren alaşımı T 1 sıcaklığına karşı gelen (2) noktasında inceleyecek olursak;
(2) den çizilen T 1 sıcaklık yatayı sınır çizilerini a
ve b noktalarında keser.
T1 yatayının sıcaklık eksenini kestiği c
noktasında arı A metali sıvı halde bulunur.
A metaline bu sıcaklıkta B metal katılırsa sıvı
eriyik oluşur,
T1 sıcaklığı sabit tutularak B nin miktarı
arttırılırsa likidüs eğrisi üzerindeki a noktasına
kadar yalnız sıvı faz bulunur ve
a noktasında %B1 bileşimine ulaşınca sıvı faz B
atomlarınca doymuş hale gelir. Daha fazla B
katılırsa sıvı fazın yanında katı faz oluşmaya
başlar.
Sıvı faz varlığını solidüs eğrisi üzerindeki b
noktasına kadar sürdürür ve iki fazlı (a-b) aralığında sıvı fazın bileşimi yalnız %B1 olur.
Aynı düşünce ile hareket edilirse T1 sıcaklığında katı faz en az %B2 kadar B, yada en çok %A2
kadar A, atomu içerebilir.
O halde (a-b) bileşim aralığındaki katı fazın bileşimi daima %B2 olur.
İşte iki fazlı bu bölgede çizilen sabit sıcaklık yatayının sınır eğrileri arasında kalan (a-b) parçasına Bağ
Çizgisi denir.
Bağ çizgisinin sıvılık eğrisini kestiği noktanın bileşimi (%B1) sıvı fazın bileşimini, katılık eğrisini
kestiği noktanın bileşimi de (%B2) katı fazın bileşimini verir. Bu yönteme Bağ Çizgisi Kuralı denir.
c) Fazların Miktarı
Bir fazlı bölgede mevcut fazın miktarı alaşımın miktarına eşittir. İki fazlı bölgedeki fazların miktarları ise
aşağıda açıklanan Levye (Kaldıraç) Kuralı yardımı ile bulunur. Bu kurala göre;
Yukarıdaki şekilde gösterilen %Bo bileşiminde Po gr alaşım ele alınsın. Bu alaşımda T 1 sıcaklığında
(2) noktasında bulunan sıvı fazın ağırlığı Ps, ile katı fazın ağırlığı Pk nın saptanması isteniyor.
Bu iki bilinmeyeni hesaplamak için iki denkleme ihtiyaç vardır. Birinci bağıntı alaşımın toplam
ağırlığının sıvı ve katı fazın ağırlıklarının toplamına eşitliğidir. (Po = Ps + Pk) ……………..………… (1)
İkinci bağıntı ise, alaşım içinde bulunan A ve B atomlarının fazlara göre dağılımı göz önüne alınarak
elde edilir.
31
MALZEME BİLİMİ
Faz Dönüşümleri ve Faz Diyagramları
(2) alaşım noktasında uygulanan bağ çizgisi kuralı ile sıvı fazın bileşiminin %B 1, katı fazın bileşiminin
%B2 olduğu saptanır.
Po gr alaşımda bulunan B atomlarının toplam ağırlığı : (% B0/100) x Po,
Ps gr sıvıda bulunan B atomlarını ağırlığı ……….…... : (% B1/100) x Ps,
Pk gr katıda bulunan B atomlarının ağırlığı ………….. : (% B2/100) x Pk dır.
Sıvı ve katı fazda bulunan B atomların ağırlıklarının toplamı alaşımdaki B atomlarının toplam ağırlığına
eşit olduğuna göre;
……………..……………...… (2)
Elde edilen bu iki denklemin ortak çözümü ile sıvı fazın miktarı;
………….…..…………………..…...… (3)
Belirlenen bu sıvı fazın miktarı Po dan çıkarılırsa geriye katı fazın miktarı Pk bulunur.
Faz diyagramında yatay eksen doğrultusundaki uzaklıklar bileşimle orantılı olduğuna göre;
X
X2 = (B2 – B0)
X = (B2 – B1) olduğundan (3) denkleminde yerine koyularak,
X1
X2
Belirli bir fazın bağıl miktarının bağ çizgisi üzerindeki (2) alaşım noktasının karşı tarafındaki kolunun
toplam boya oranına eşit olduğu sonucu çıkarılır ve buna Levye Kuralı denir.
Örnek: Bir bakır (Cu) – Nikel (Ni) alaşımının, 1250 oC sıcaklıkta sıvı
faz bileşimi %32 ve katı faz bileşimi %43 olarak soğuma
diyagramları yardımıyla belirlenmiştir. Bu sıcaklık ve %35 bileşimde
alaşımın sıvı ve katı fazın oranlarını levye kuralına göre belirleyiniz.
bu
Ps = (43-35)/(43-32) = %0,73
Pk = (35-32)/(43-32) = %0,27
Po = Ps + Pk,
Pk = Po – Ps = 1,00 – 0,73 = %0,27
32
MALZEME BİLİMİ
Malzemelerin (Mekanik) Özellikleri
MALZEMELERİN ÖZELLİKLERİ
Malzeme biliminin amacı; önce malzemelerin içyapısını incelemek, sonra içyapılarla özellikler
arasındaki ilişkileri araştırarak, geliştirilecek temel ilke ve kavramlar ışığında uygulamada kullanılan
malzemeleri tanımaktır.
Bu bölüme kadar malzemelerin içyapı özellikleri ele alındı, bu bölümde ise malzemelerin uygulama
yönünden önemli özelliklerine ayrıntılı olarak yer verilecektir.
Malzemelerin mühendislik özellikleri 3 ana grupta incelenebilir. Bunlar;
1. ELEKTRİKSEL Özellikler (İletkenlik, yarı-iletkenlik, di-elektrik, manyetik, optik ve ısıI özellikler)
2. FİZİKSEL Özellikler (Birim ağırlık, boşluk oranı, geçirimlilik, akustik özellikler gibi)
3. MEKANİK Özellikler (Dayanım, birim şekil değiştirme, E-modülü, poisson oranı gibi)
Elektriksel özellikler, malzemelerin elektron yapısına, bağ türüne ve içyapı özelliklerine büyük ölçüde
bağlı olup, özellikle elektronik endüstrisi uygulamalarında büyük önem arz etmektedir.
Fiziksel özellikler, diğer birçok alanda olduğu gibi inşaat mühendisliği uygulamalarında da yapı
malzemelerinin birim ağırlık, boşluk oranı ve geçirimlilik gibi özellikleri yapı fiziği ve kalıcılık konularını
ilgilendiren önemli özelliklerdir.
Mekanik özellikler ise, uygulamada zorlamaya (kuvvete) maruz kalacak malzemelerde aranan en
önemli özelliklerdir. Yapı sistemlerinin mukavemet hesaplarında dayanım, birim şekildeğiştirme ve
elastisite modülü gibi mekanik özelliklerin iyi bilinmesi gerekir.
MALZEMELERİN MEKANİK ÖZELLİKLERİ
Bir malzemenin kendisine uygulanan kuvvetlere karşı gösterdiği tepkiler mekanik davranış olarak
tanımlanabilir. Bu davranış, malzemelerin değişik türden zorlamalar altında oluşan gerilme ve şekil
değiştirmelerin ölçülmesi ve incelenmesiyle saptanır. Öyle ki, cisimler artan dış zorlamalar (kuvvetler)
altında önce şekil değiştirir, sonra dayanımını yitirerek kırılırlar. Kırılma sınırına kadar malzemelerde
elastik ve plastik türden farklı şekil değiştirme davranışları görülebilir.
Düşük gerilmeler altında meydana gelen şekil değiştirmeler elastik, yani yük kaldırıldığında tümüyle
geri dönebilen (tersinir), bir başka değişle yük kaldırıldığında cismin yük uygulanmadan önceki şekline
aynen dönebildiği türdendir.
Gerilmeler elastik sınırı aşarsa şekil değiştirmeler plastik, yani kalıcı, bir başka değişle yük
kaldırıldığında cismin yük uygulanmadan önceki şekline aynen dönemediği türdendir.
Bu farklı karakterli şekil değiştirme davranışları, mühendislik uygulamalarında bilinmesi gerekli Rijitlik
ve süneklik gibi diğer bazı mekanik özellikleri ortaya çıkarır.
Elastik davranışla ilgili Elastisite (Young) Modülü veya Rijitlik özellikleri; malzemenin elastik şekil
değiştirmeye karşı gösterdiği direnci ifade ederken, plastik davranışla ilgili süneklik özelliği;
malzemenin plastik şekil değiştirebilme yeteneğini gösterir.
Bunun yanında, malzemelerin hem elastik hemde plastik şekil değiştirme davranışıyla ilgili olan
mukavemet (bir başka değişle dayanım) özelliği; dış kuvveler altında malzemede kırılma oluşturan bir
gerilme sınırı olarak tanımlanabilir.
33
MALZEME BİLİMİ
Malzemelerin (Mekanik) Özellikleri
Genel olarak malzemelerin mekanik özelliklerinde atomlararası bağlar belirleyici rol oynamakla
beraber, elastik davranışla ilgili olan Elastisite Modülü veya Rijitlik özelliği içyapıya ve deney
koşullarına bağlı olmayıp, atomlararası bağlar tarafından belirlenir. Ancak plastik davranışa ilişkin
süneklik, mukavemet ve sertlik özellikleri içyapıya ve deney koşullarına büyük ölçüde bağlıdır.
Malzemelerin mekanik özellikleri arasındaki büyük farklılıkları açıklayabilmek için, şekildeğiştirme
sürecinde atomların nasıl davrandıkları ve içyapıda ne gibi değişmeler oluştuğunu bilmek gerekir. Öğle
ki, içyapıyı değiştiren etkenler malzeme özelliklerini de değiştirir. Nitekim bu etkenler ve bunların
uygulama yöntemleri iyi bilinirse içyapıda gerekli değişiklikler yapılarak, özellikler malzemenin kullanım
amacına uygun olarak ayarlanabilir. Ancak bu ayarlamalar doğal olarak sınırlıdır.
Malzemelerin mekanik özellikleri iki farklı yaklaşımla incelenebilir. İlk yaklaşımda; malzemenin
uygulanan kontrollü dış kuvvetler altında tepkisi uygula-gözle yöntemiyle deneysel olarak saptanır. Bu
yöntemde içyapıdaki davranış ve değişiklikler dikkate alınmaksızın, uygulanan kuvvetlerin malzemede
neden olduğu gerilmelere karşılık oluşan şekildeğiştirmeler ölçülür. Bu şekilde, belirli koşullar altında
deneylerle elde edilen gerilme-şekil değiştirme bağıntılarına Bünye Denklemleri denir. Bu
denklemler, dış kuvvetler altında oluşacak gerilme ve şekildeğiştirme analizlerinde kullanılır.
Gerçekte bu yaklaşımla mekanik davranışlar incelenirken malzemenin içyapısını bilmeye gerek yoktur,
ancak gerilme, şekildeğiştirme, mukavemet, sertlik ve süneklik gibi mekanik özelliklerin içyapı ile
ilişkilerini (Örneğin, kristal yapılı malzemelerde tane büyüklüğü artarsa sertlik ve mukavemet yükselir,
süneklik azalır) açıklayabilmek için bu kavramları bilmek gerekir.
İkinci yaklaşımda ise; şekildeğiştirme ve kırılma süreçlerinde atomların nasıl davrandığı, içyapıda
mikro düzeyde ne tür değişikliklerin oluştuğu, içyapılarla mekanik özellikler arasında ne gibi ilişkilerin
bulunduğu, diğer bir deyimle şekildeğiştirme ve kırılmanın mekanizmaları ele alınır.
MEKANİK DAVRANIŞ
Mekanik davranış incelenirken, malzemelerin homojen ve sürekli ortam oldukları varsayılır. Mekanik
davranışı parça boyutlarından soyutlayarak genelleştirmek için; kuvvet yerine gerilme, boyutlarda
oluşan değişmeler yerine ise birim şekildeğiştirme (veya şekildeğiştirme oranı) kavramları kullanılır.
Gerilme; parçaya etkiyen toplam kuvvetin enkesitte birim alana düşen miktarını,
Birim Şekildeğiştirme; ise toplam şekildeğiştirmenin birim boya karşı gelen miktarını, ifade eder.
Deneysel çalışmalarla elde edilebilen ve malzemelerin bu iki önemli mekanik davranış özelliği
arasındaki ilişkiyi gösteren gerilme-birim şekildeğiştirme (σ–ε) eğrileri, malzemelerin mekanik
davranışlarıyla ilgili çok yararlı bilgiler sağlarlar.
Gerilme Kavramı
Dış kuvvetlerin etkisi altındaki bir malzeme parçasında, denge halindeki dış kuvvetlerin oluşturduğu iç
kuvvet, yani gerilmeler, herhangi bir hayali enkesit düzlemi üzerinde denge denklemleri yardımıyla
şekildeki gibi gösterilebilir.
34
MALZEME BİLİMİ
Malzemelerin (Mekanik) Özellikleri
Enkesit Alanı
A=bxc
c
b
Malzeme parçasına etkiyen (F) toplam dış kuvvet, (N) normal bileşen ve (T) teğetsel bileşenine
ayrılabilir. (N) normal bileşenin yönü içeriye doğru ise basınç, dışarıya doğru ise çekme etkisi
(gerilmeleri) oluştururken, (T) teğetsel bileşen enkesit yüzeyine paralel olup kayma yada kesme etkisi
(gerilmeleri) oluşturur.
Eksenel ve teğetsel kuvvetleri etkiledikleri enkesit alanına bölerek, bu kuvvetleri parça boyutlarından
bağımsız olarak normal (σ) ve kayma (δ) gerilmeleri şeklinde ifade edebiliriz.
=
ve
=
(
kgf
N
(MPa) gibi birimlerde)
veya
cm
mm
Malzemeler uygulama koşullarında çoğunlukla lineer elastik davranış gösterirler. Bu tür davranışta,
aynı anda uygulanan iki farklı gerilmenin (normal ve kayma) birlikte oluşturduğu etki, bu gerilmeler ayrı
ayrı uygulandıklarında oluşturdukları etkilerin toplamına eşittir. Bu ilkeye göre bileşik zorlama,
şekildeki basit çekme ile basit kayma hallerinin süperpozisyonu şeklinde ifade edilebilir.
Şekil Değiştirme Kavramı
Gerilmeler etkisinde malzemelerin boyutları değişir; çekme halinde boy uzar ve en daralır, basınç
halinde ise boy kısalır ve en genişler. Kayma etkisinde ise yalnız açılar değişir. Boyutlardaki bu
değişmeler, birim şekildeğiştirme veya şekildeğiştirme oranı olarak ifade edilir. Bunun için, son boy
(L)’den ilk boy (Lo) çıkarılır ve bu fark ilk boya bölünerek, sonuç yüzde (%) olarak ifade edilir.
35
MALZEME BİLİMİ
Malzemelerin (Mekanik) Özellikleri
L
Şekil Değiştirmeler
Çekme etkisinde (a)
Basınç etkisinde (b)
Eksenel birim şekil değiştirme
εa = (L – Lo) / Lo = ΔL / Lo, (+)
εa = (h – ho) / ho = Δh / ho, (–)
Yanal birim şekil değiştirme
εy = (d – do) / do = Δd / do, (–)
εy = (d – do) / do = Δd / do, (+)
Kayma etkisinde şekil değiştirmeler (c)
Kayma birim şekil değiştirmesi
= Δx / h = tan
Lineer elastik malzemelerde küçük gerilmeler altında yanal şekil değiştirme (εy), eksenel şekil
değiştirme (εa) ile orantılıdır ve bu orantı katsayısına Poisson Oranı ( ) denir.
= εy / εa
Basit kayma etkisinde ana boyutların değişmediği, yalnız açıları değiştiği varsayılır. Kayma şekil
değiştirmesi dik açılardaki değişmenin tanjantı ile belirtilir.
Gerilme-Şekil Değiştirme İlişkisi ve Bağıntıları
Malzemeler düşük gerilmeler altında çoğunlukla lineer elastik davranış gösterirler. Lineer elastik
davranışta gerilmeler ile şekildeğiştirmeler orantılıdır ve şekildeğiştirmeler elastik tersinirdir (yani geri
dönebilir). Bu davranış aşağıdaki Hooke Kanunu ile ifade edilir;
σ=Exε
Burada, E; Elastisite Modülü, yani malzemenin elastik şekil değiştirmeye karşı gösterdiği direnç veya
Rijitlik anlamına gelir. Örneğin çeliğin elastisite modülü alüminyumunkinin 3 katı kadardır. Buna göre
aynı boyutta alüminyum ve çelik çubuğa elastik bölgede eşit yük uygulanırsa alüminyum çelikten 3 kat
daha fazla uzar, kiriş halinde ise 3 kat daha fazla çöker.
Lineer elastik malzemelerde (δ) kayma gerilmesi ile (γ) kayma şekil değiştirmesi orantılıdır ve G orantı
katsayısına Kayma Modülü (G) denir.
δ=Gxγ
Normal ve kayma gerilme durumları için ayrı ayrı verilen bu iki bağıntı;
(Gerilme = Modül x Birim Şekil Değiştirme) ifadesi ile genelleştirilebilir.
36
MALZEME BİLİMİ
Çelik Çekme Deneyi ve Çekme Etkisinde Davranış
Çelik Çekme Deneyi ve Çekme Etkisinde Malzemelerin Davranışı
Yapı elemanlarının mukavemet hesaplarında malzemelerin gerekli
dayanım, birim şekil değiştirme, elastisite modülü ve poisson oranı
gibi mekanik özelliklerini belirlemek amacıyla, genelde daire kesitli
veya dikdörtgen kesitli çubuklar üzerinde Çekme Deneyi yapılır.
Bir hidrolik çekme aletinde konik çeneler arasına tespit edilen deney
çubuğu basınçlı yağ etkiyen bir piston yardımı ile çekilir. Yağ
basıncından pistona etkiyen yük ölçülür. Ayrıca parçanın üstüne
tespit edilen bir ekstansometre yardımıyla da uzamalar ölçülür.
Yükü kademe kademe arttırarak uygulanan gerilmelerle (σ), oluşan
şekil değiştirmelerin (ε) değişimi şekildeki gibi bir (σ–ε) diyagramı
halinde gösterilir. Bu gerilme-birim deformasyon (σ–ε) grafikleri,
malzemelerin mekanik özellikleri ve davranışı hakkında önemli
bilgiler sağlar.
N yükü etkisinde oluşan gerilme
Numunenin enkesit alanı
N yükü altında (ilk boy) Lo boyunda oluşan uzama miktarı
Şekil değiştirme oranı (birim boydaki uzama miktarı)
σ = N / Ao
Ao = π x do2 / 4
ΔL = L - Lo
εa = (L - Lo) / Lo = ΔL / Lo
e
E=tan
%0.2
Gerilme – Birim Deformasyon (σ–ε) Grafiği
37
MALZEME BİLİMİ
Sembol
Çelik Çekme Deneyi ve Çekme Etkisinde Davranış
Notasyonlar
σ
Normal veya eksenel gerilme (basınç veya Çekme gerilmesi)
δ
Kayma (kesme veya makaslama) gerilmesi
E
Normal gerilme durumunda Elastisite Modülü
G
Kayma gerilmesi durumunda Kayma Modülü
ε
Birim şekil değiştirme (şekil değiştirme oranı)
εa
Eksenel şekil değiştirme
εy
Yanal şekil değiştirme
γ
Kayma şekil değiştirmesi
σp
Orantılılık sınır gerilmesi
σe
Elastik sınır gerilmesi
σa
Akma sınır gerilmesi (akma dayanımı)
σç
Çekme sınır gerilmesi, maksimum gerilme (çekme dayanımı)
σk
Kopma sınır gerilmesi (kopma dayanımı)
Çekme deneyine başlandığında, numuneye uygulanan kuvvet (çekme) arttırıldıkça oluşan gerilmeler
ve deformasyonlar da artmaya başlar. Elastik sınıra (orantılılık sınırı) kadar, gerilmeler ve şekil
değiştirmeler orantılı olarak artar, grafik doğrusal olur ve dolaysıyla bu bölgede Hooke Kanunu
(E = σ / ε) geçerlidir. Elastik sınıra kadar oluşan şekil değiştirmeler (uzamalar), numunenin çeneler
arasındaki tüm boyunda homojen olarak meydana gelir.
Cisimlerin büyük bir çoğunluğunda düşük gerilmeler altında şekil değiştirmeler elastik, yani tersinirdir.
Bu bölgede yük uygulanınca deformasyonlar oluşur, yük kalkınca geri döner. Başlangıçta grafik bir
doğruya çok yakın şekildedir, yani gerilmelerle şekil değiştirmeler orantılıdır. Bu oranı sabitine
Elastisite Modülü (E) denir ve lineer bölgede eğriye çizilecek teğetin eğimine eşittir (E = σ / ε = tanα).
Orantılık sınır gerilmesine kadar oluşan şekil değiştirmeler lineer elastiktir ve bu sınıra kadar
malzemenin yük altındaki davranışı lineer elastik davranış olarak nitelendirilebilir.
Gerilmeler orantılık sınırı olan (σ p)’yi aşarsa, gerilmeler ile şekil değiştirmeler artık orantılı ilerlemez,
aralarındaki sabit oran bozulur ve Hooke Kuralı geçerli olmaz. Ancak elastik sınır (σe)’ye kadar olan
dar bölgede oluşan şekil değiştirmeler yine elastik yani geri dönebilir türdendir, dolayısıyla non-lineer
elastik davranış söz konusudur.
Gerilmeler elastik sınır (σe)’yi aşacak olursa, plastik (kalıcı) şekil değiştirmeler oluşmaya başlar.
Malzemede oluşan toplam şekil değiştirmenin bir kısmı elastik olup yük boşaltılınca kaybolur, fakat bir
kısmı ise kalıcıdır. Bu plastik bölgede, yük kaldırılıp tekrar yüklenecek olursa, oluşan boşaltma ve
tekrar yükleme eğrisi yine bir doğrudur ve diyagramın başlangıçtaki kısmına paralel olur. Buradan
çıkan sonuca göre; plastik bölgede de elastik şekil değiştirmeleri karakterize eden elastisite modülü
aynıdır ve elastik bileşen için de Hooke Kuralı geçerlidir.
Bu bölgede toplam şekil değiştirme (ε)’nin iki bileşeni vardır. Biri elastik bileşen (εe), diğeri ise plastik
bileşen (εp) dir. Elastik bileşen εe = σ / ε bağıntısı ile hesaplanabilir. Buna göre; ε = εe + εp olur.
38
MALZEME BİLİMİ
Çelik Çekme Deneyi ve Çekme Etkisinde Davranış
Elastik sınır, yükleme-boşaltma deneyleri ile saptanabilse de pratik olmadığından bu yöntem
kullanılmaz. Bunun yerine plastik bölgenin başlangıcı olarak Akma Sınırı alınır. Akma Sınırı veya
Akma Dayanımı yada Mukavemeti %0,2 plastik şekil değiştirme oluşturan gerilme olarak tanımlanır.
Bu tanımdan yararlanılarak, akma sınırını bulmak için sürekli yükleme ile elde edilen (σ-ε)
diyagramının şekil değiştirme ekseni üzerinde %0,2 noktası işaretlenir ve bu noktadan diyagramın
doğrusal kısmına paralel çizilir. Bu paralelin eğriyi kestiği noktaya karşı gelen gerilme akma sınırıdır.
Kuvvet arttırılmaya devam edilirse bir (Nm) maksimum değere ulaşınca artış durur, sonra azalmaya
başlar ve bu anda çubuğun bir bölgesinde kesitin daraldığı yani büzüldüğü (boyun verme) görülür.
Maksimum kuvvete kadar olan uzamalar üniformdur, silindir biçimindeki parça boyca artıp çapça
daraldığı halde silindir biçiminde kalır. Büzülmeye başladıktan sonra yalnız bu bölgede ek uzamalar
oluşur, kesit gittikçe daralır, diğer bölgelerde ise uzama olmaz, dolayısıyla uzamalar üniform değildir.
Büzülen bölgedeki uzamaları oluşturmak için daha az kuvvet gerektiğinden kuvvet ibresi düşmeye
başlar, oysa gerçekte gerilmeler sürekli artar ve sonunda Nk kopma kuvvetinde parça koparak ikiye
bölünür.
Çekme mukavemeti (σç), çubuğun taşıyabileceği maksimum Nm kuvvetini ilk kesite bölerek elde edilir;
σç = Nm / Ao
Kopma mukavemeti (σk), kopma anındaki Nk kuvvetini ilk kesit alanına (Ao) bölerek elde edilir.
σk = Nk / Ao
Gerçek kopma mukavemeti (σgk) ise, Nk kopma kuvvetini en dar kesit alanına (As) bölerek elde edilir.
σgk = Nk / As
Yukarıdaki şekilde dolu çizgi ile gösterilen (σ-ε) eğrisi görünen (mühendislik) gerilme-birim şekil
değiştirme eğrisi olup, gerilme ve şekil değiştirmeler ilk boyutlara göre hesaplanmaktadır. Oysa
gerçekte bu değerlerin anlık boyutlara göre hesaplanması gerekir ve şekilde kesikli çizgi ile gösterilen
gerçek gerilme-birim şekil değiştirme eğrisi elde edilir. Nitekim gerçek kopma mukavemeti (σgk),
görünen kopma mukavemeti (σ k)’dan çok daha büyüktür.
Süneklik, Tokluk ve Rezilyans Kavramları
Bir malzemenin plastik şekil değiştirme yeteneğine SÜNEKLİK denir. Bu özellik çekme deneyinde,
kopma anında oluşan toplam plastik şekil değiştirme veya kopma uzama oranı ile belirtilir.
Çekme deneyinde çubuğun sünekliği (εk), çubuğun deney öncesinde ölçü boyu (Lg) ile deney
sonundaki son boyuna (Ls) bağlı olarak;
bağıntısı yardımıyla hesaplanır ve % olarak ifade edilir.
Büzülme başlamadan önce oluşan şekil değiştirmeler üniformdur ve şekil değiştirme oranı ölçü boyu
Lo’dan bağımsızdır. Ancak büzülme başladıktan sonra uzamalar yalnız büzülme bölgesinde yerel
olarak üniform olmayan bir biçimde artmaya devam eder ve bu bölge dışında durur. Bu durumdan
dolayı, malzemede hesaplanacak süneklik değerini numune boyutlarından bağımsız hale getirmek için
dairesel kesitli deney parçasının Ölçü Boyu; uzun çubukta Lg = 10.do, kısa çubukta Lg = 5.do alınır.
39
MALZEME BİLİMİ
Çelik Çekme Deneyi ve Çekme Etkisinde Davranış
Uygulamada kolaylık için, çubukların üzeri şekildeki gibi birer santim ara ile işaretlenir. Kopmadan
sonra iki parça uç uca getirilir. Lg ölçü boyuna karşı gelen çizgi sayısının yarısı kadarı kopma
bölgesinin solunda, yarısı kadarı da sağda sayılır, bu şekilde elde edilen iki sınır çizgisinin arası
ölçülerek Son Boy Ls bulunur.
Malzemelerin gerilme-birim deformasyon eğrilerinden elde edilebilecek bir diğer mekanik özellik olan
TOKLUK; malzemelerin kırılma anına kadar sönümleyebildiği toplam enerji yada birim hacimdeki
herhangi bir cismi kırmak için gerekli olan enerji miktarı olarak tanımlanabilir.
Bu enerji, (σ-ε) eğrisin in kırılma noktasına kadar altında kalan bütün alana eşittir ve kuvvet etkisinde
şekil değiştirme işi yapan cisim için iş-enerji bağıntıları yardımıyla aşağıdaki gibi ifade edilebilir.
Çubuğa (P) kuvvetinin uygulandığı ve (ΔƖ) uzamasının oluştuğu bir durumda, çubuğun boyunu küçük
(δƖ) kadar arttırmak için yapılacak iş (P- δƖ) dikdörtgeninin taralı alanına eşittir.
dw = P. δƖ
Başlangıçtan itibaren (ΔƖ) kadar bir uzama sağlamak için yapılan toplam iş;
∆
=
.
40
MALZEME BİLİMİ
Çelik Çekme Deneyi ve Çekme Etkisinde Davranış
(P = σ . A) ve (δl = l . dε) ifadeleri integralde yerine konursa;
=
. . .
Deney öncesi ve sonrası numune hacminin değişmediği kabulünden hareketle (Vo = Ao . lo = A . l);
=
. .
Denklemin her iki tarafı Vo sabiti ile bölünürse birim hacimde yapılan iş;
=
.
Bu bağıntıdan anlaşıldığı gibi; bir cismin birim hacminde (ε) uzama oranı için oluşturulan şekil
değiştirme enerjisi gerilme-şekil değiştirme eğrisinin altında kalan alana eşittir ve aşağıdaki bağıntı
yardımıyla hesaplanabilir.
=
.
Aşağıda, endüstriyel çeliklerde (σ-ε) eğrilerinin karbon (C) oranına bağlı olarak değişimleri
görülmektedir. Yumuşak çeliğin (%0,1 karbonlu) mukavemeti düşük olmakla beraber tokluğu çok
büyüktür, bu nedenle karayollarında emniyet bariyerlerinde ve taşıtların tamponlarında kullanılmaya
elverişlidir. Çünkü çarpma halinde büyük enerji yuttuktan sonra kırılırlar.
Yüksek karbonlu çeliklerin mukavemeti büyük, fakat tokluğu çok azdır, çarpma etkisinde az enerji
yutarak kırılır. Bu çelikler aşırı zorlanmaya ve aşınmaya maruz parçaların üretimine elverişlidir.
Malzemelerin gerilme-birim deformasyon eğrileri yardımıyla elde edilebilen REZİLYANS özelliği ise;
kısaca bir malzemenin elastik şekil değiştirme yeteneği veya bir cisimde plastik şekil değiştirme
oluşturmaksızın birim hacimde depo edilebilecek maksimum elastik şekil değiştirme enerjisi olarak
ifade edilebilir.
Bu enerji ise, (σ-ε) eğrisinde elastik deformasyon sınırına kadar eğrinin altında kalan alana eşittir ve
yine iş-enerji bağıntıları yada daha basitçe eğrinin bu bölgede lineere yakın olması kabulüyle oluşan
dik üçgenin alan bağıntılarıyla hesaplanabilir.
41
MALZEME BİLİMİ
Çelik Çekme Deneyi ve Çekme Etkisinde Davranış
Lineer-elastik bölgede oluşan dik üçgenin alanı için;
=
.
=
Lineer-elastik bölgede geçerli Hooke Kanunu gereğince;
σ=E.ε
Gerilme ve E-Modülüne bağlı olarak Rezilyans aşağıdaki
bağıntı yardımıyla hesaplanabilir.
=
=
( .
)
Çekme Etkisinde Malzemelerin Davranışı
Mekanik davranış yönünden malzemeler iki sınıfa ayrılırlar;
a) GEVREK Malzemeler
b) SÜNEK Malzemeler
a) Gevrek Malzemeler
Elastik bölge sonunda plastik şekil değiştirmeden aniden kırılırlar, gerilme-şekil değiştirme eğrileri eğik
doğru biçimindedir. Bu tür malzemelerde elastik sınır, akma gerilmesi ve çekme mukavemeti eşittir.
Belirgin bir büzülme (boyun verme) veya genişleme olmadan az bir enerji ile kırılırlar, toklukları çok
azdır.
Aşağıda farklı mekanik davranışlar gösteren çeşitli malzemelere ait gerilme-birim deformasyon eğrileri
gösterilmiştir. Şekildeki Cam ve Al2O3 gibi dökme demir (pik) beton, taş ve tuğla gevrek malzemelere
gösterilebilecek örneklerdir.
42
MALZEME BİLİMİ
Çelik Çekme Deneyi ve Çekme Etkisinde Davranış
b) Sünek Malzemeler
Önemli ölçüde plastik şekil değiştirme yaptıktan sonra büzülerek kırılırlar, kırmak için oldukça büyük
enerjiye gerek vardır, yani toklukları yüksektir.
Sünek malzemelerin gerilme-şekil değiştirme diyagramları, başlangıçtaki elastik davranışlarını
gösteren tipik bir doğrusal kısımdan sonra yatıklaşarak eğri biçimini alır.
Yukarıdaki (σ-ε) eğrilerinden göreceli olarak daha iyi anlaşılacağı gibi; arı alüminyum plastik şekil
değiştirdikten sonra belirgin şekilde büzülür ve kopma noktasında kesit sıfıra yaklaşır. Bu %100’e
yakın büzülme davranışından dolayı tam sünek malzeme sayılan arı alüminyumdan başka, bakır ve
alaşımları, alüminyum alaşımları ile çeliklerin çoğu (yapı çelikleri de), tipik olarak önce plastik şekil
değiştirip sonra biraz büzüldükten sonra kopan sünek malzeme örnekleridir.
Öte yandan, az karbonlu S220 yumuşak çeliğin (σ-ε) diyagramında, şekil (c) de görülen belirgin bir
akma basamağı (akma sahanlığı) dikkati çeker. Öğle ki gerilme, akma sınırına ulaşınca önce biraz
azalır, akma sürecinde yaklaşık sabit kalır ve akma bitince tekrar artmaya devam eder.
Plastik deformasyonların oluşumuyla birlikte içyapıda ilerleyen dislokasyon hareketlerinin (kusurların
ilerleyişinin) tane sınırlarında bir miktar engellenmesi nedeniyle gerçekleşen bu dayanım artışı
Pekleşme Olayı olarak bilinir.
Basit çekme halinde akmayı oluşturan maksimum kayma gerilmeleri eksenle 45° açı yapan eğik
düzlemler boyunca etkir ve kırılma yüzeyi koni-çanak biçiminde olur. Akmadan sonra gerilmeler artar,
eğri yükselerek yatıklaşır, bir maksimuma erişince büzülme başlar ve gerilme azalarak eğri kopma
noktasında sona erer.
Lineer polimerler (Termoplastikler) çoğunlukla sünek davranış gösterirler. Yukarıda, polietilen (PE) ve
Polivinil klorürün (PVC) gerilme-birim deformasyon eğrileri şekil (d)’de görülmektedir.
Uzay ağı polimerleri (Termoset plastikler) ise sürekli kovalent bağ yapıları nedeniyle plastik şekil
değiştirmezler, dolayısıyla gevrek niteliktedirler. Yukarıdaki şekil (d)’de tipik bir Termoset plastik olan
bakalitin (σ-ε) diyagramı görülmektedir.
Endüstriyel malzemelerin büyük bir çoğunluğu lineer elastik olduğu gibi plastik bölgede de şekil
değiştirmenin elastik bileşeni bu niteliğini korur ve elastisite modülü değişmez, ancak bazı malzemeler
lineer olmayan elastik davranış gösterirler. Bu tür malzemelerin en ilginç örneği; (σ-ε) diyagramı şekil
(e)’de gösterilen doğal kauçuktur. Kauçuk, kuvvet etkisinde büyük ölçüde elastik şekil değiştirir ve şekil
değiştirme arttıkça elastisite modülü yükselir.
43
MALZEME BİLİMİ
Basınç, Kesme ve Eğilme Etkisinde Davranış
Basınç Etkisinde Davranış
Malzemelerin yüzeyinden içeriye doğru etkiyen kuvvetler basınç gerilmeleri oluşturur. Basınç kuvveti
altında parçanın boyu azalır, yanal doğrultuda ise genişler. Başlangıçtaki şekil değiştirmeler elastik
yani tersinirdir ve gerilmelerle orantılıdır. Çekme ve basınçta elastik sabitler (E-Modülü gibi) genellikle
eşittir.
Ancak yük arttıkça orta bölgeler serbestçe genişlerken, uç kısımlarda tabla ile numune arasındaki
sürtünme kuvvetleri yanal genişlemeyi kısıtlar. Orta kısımlarda genişleme dolayısıyla atomlararası
uzaklık artmaya zorlanır, bu da yanal çekme gerilmeleri doğurur. Bu durumda basit basınç hali,
eksenel yönde basınç ve yanal yönde çekme gerilmelerinden oluşan çok eksenli gerilme haline
dönüşür. Bu karmaşık gerilme hali nedeniyle numunenin biçimi ve boyutları mekanik davranışı önemli
ölçüde etkiler.
İzotrop sünek malzemelerde basınç altındaki davranış çekmedekine benzer, elastisite modülleri ve
akma sınırları eşittir. Gerçekte akma olayı maksimum kayma gerilmesi etkisinde oluşur. Eksenel
yüklemede maksimum kayma gerilmeleri eksenle 45° açı yapan düzlemler boyunca etkir ve değeri
eksenel gerilmenin yarısına eşittir.
Akmadan sonra deney parçasının orta kısmı belirgin olarak genişler, uçlar sürtünme etkisiyle dar kalır,
sonuçta fıçı biçimini alır. Kesit büyüdüğünden taşıyabildiği yük, yani gerilme de sürekli artar.
Basınç etkisinde gerilme-şekil değiştirme diyagramı çekmedekinin orijine göre yaklaşık simetriği olur.
İzotrop yapılı metallerde akma gerilmeleri çekme ve basınçta eşittir. Sünek malzemelerde basınç
deneyine gerek yoktur. Gevrek malzemelerde ise çekme ve basınç mukavemetleri arasında büyük
fark vardır.
44
MALZEME BİLİMİ
Basınç, Kesme ve Eğilme Etkisinde Davranış
Gevrek malzemelerde düşük basınç gerilmeleri altında şekil değiştirmeler tersinirdir ve gerilmelerle
orantılıdır, elastisite modülü çekmedekine eşittir, ancak elastik sınırlarla, kırılmanın oluştuğu
mukavemet değerleri çok farklıdır. Basınç etkisinde kırılma ya kayma etkisinde veya çekme etkisinde
oluşur. Malzemenin türü, deney parçasının biçimi ve boyutları kırılma türünü ve basınç mukavemetini
çok etkiler. Parçanın boyu kısa ise, yukarıdaki şekilde (b) görüldüğü gibi kayma etkisinde kırılır, uzun
ise orta kısımda yanal doğrultuda oluşan çekme gerilmelerine dik yönde yarılma şeklinde olur.
Çağımızda, yapı üretiminde sağladığı önemli avantajları nedeniyle çok yaygın bir şekilde kullanılan ve
gevrek bir malzeme olan betonun en önemli özelliği basınç dayanımıdır. Nitekim betonun basınç
dayanımını tespit etmek veya kontrol etmek amacıyla beton basınç deneyi yapılır. Beton basınç
deneylerinde genellikle çapı 10 cm, yüksekliği 20 cm yada çapı 15 cm, yüksekliği 30 cm olan standart
silindir veya 15 cm yada 20 cm boyutlu standart küp numuneler kullanılmaktadır. Yukarıda
bahsedildiği gibi, numunelerin boyut özelliklerinin bir sonucu olarak; narinlik oranı
(λ=yükseklik/genişlik) 1 olan küp numuneler, yük ekseniyle yaklaşık 45o açıda oluşan kırılma
yüzeylerinde etkili kayma gerilmeleri nedeniyle kırılırken, narinlik oranı 2 olan silindir numuneler,
kırılma yüzeylerinin oluşturduğu konik kama kısımları arasında yarılmaya zorlanan orta bölgede etkili
yanal çekme gerilmeleri etkisinde kırılır. Betonun en zayıf özelliği olan çekme dayanımı kayma
dayanımından daha küçük olduğundan, aynı beton yığınından hazırlanan silindir numunelerde
belirlenen dayanım silindir numunelerden daha küçük olur. Öğle ki, bu konuda yapılan bilimsel
çalışmalarla, aynı betonun karakteristik silindir numune dayanımı, karakteristik küp numune
dayanımının yaklaşık 0,85’i (yani %85’i) olduğu şeklinde bir ilişki tespit edilmiş ve kabul görmüştür.
Hatta, ülkemizde beton dayanım sınıflarını tanımlayan C25/30 veya C30/37 gibi beton dayanım
sınıflarında, ( / ) işaretinin solundaki ilk sayılar silindir numune dayanımını, ( / ) işaretinin sağındaki
sayılar ise küp numune dayanımını ifade etmektedir.
Kayma (Kesme) Etkisinde Davranış
Basit kayma etkisinde, parça ana boyutlarının değişmediği, yalnız açıların değiştiği önceki bölümlerde
belirtilmişti. Sünek malzemelerde ( ) kayma gerilmeleri ile ( ) kayma şekil değiştirmeleri arasındaki
( - ) ilişki grafiği ve ilgili bağıntılar aşağıdaki gibidir.
Düşük gerilmeler altında davranış lineer elastiktir, yani Hooke kuralı geçerlidir ve ( - ) eğrisinin eğimi
kayma modülünü verir. Fakat akma başladıktan sonra eğri yatıklaşır, kırılma oluşuncaya kadar
gerilmeler sürekli artar. Kırılma, kayma gerilmeleri etkisinde kesilme şeklinde oluşur, büzülme ve
daralma gibi davranışlar oluşmaz.
45
MALZEME BİLİMİ
Basınç, Kesme ve Eğilme Etkisinde Davranış
Akma, maksimum kayma gerilmesi etkisinde oluştuğuna göre, sünek malzemelerde basit çekmede ve
basit kaymada aynı değerde oluşur. Buna göre; kaymadaki akma kayma gerilmesi ( A) basit
çekmedeki (σA) akma gerilmesinin yarısına eşittir. Diğer taraftan, basit çekme deneyi ile elde edilen
elastisite modülü ve poisson oranı, G = E / [ 2 x (1+ ) ] denklemine koyularak kayma modülü
hesaplanabilir. Tasarım hesaplarında gerekli olan (G) kayma modülü ile ( A) akma kayma gerilmesi
basit çekme deneyinin sonuçlarına göre saptanabileceğinden ayrıca kayma deneyine gerek kalmaz.
Gerçekte kayma deneyleri silindir biçimindeki numunelere burma etkisi uygulayarak yapılır.
Eğilme Etkisinde Davranış
Mühendislik yapıları, kendi ağırlıklarından kaynaklanan sabit yükler, kullanımlarından kaynaklanan
hareketli yükler ve ayrıca deprem, rüzgar gibi doğal dış yüklerin etkisinde zorlanırlar. Yapıları bu
yüklere karşı ayakta tutan taşıyıcı sistemleri, kolon ve kiriş gibi çubuk türü elemanlar ile döşeme gibi
plak türü elemanlardan oluşur. Bu taşıyıcı elemanlar, kendileriyle aynı doğrultudaki eksenlerine paralel
yönde etkiyebilen yükler (kuvvetler) nedeniyle çekme veya basınç etkilerine, eksenlerine dik yönde
etkiyebilen yükler nedeniyle ise kesme ve eğilme etkilerine maruz kalırlar.
Elemanda eğme momenti şeklinde etkiyen dış zorlamalar malzeme içinde çekme, basınç ve kayma
gerilmeleri oluşturur. Örneğin pozitif eğilme momentine maruz kalan bir basit kirişte, alt-orta kısımda
çekme gerilmeleri oluşurken, üst-orta kısımda basınç gerilmeleri doğar. Dış yükler etkisiyle artan bu
gerilmelerden biri, o malzemenin kritik (yani küçük) olan dayanım gerilmesine ulaşınca eleman kırılır.
Bu kritik değerler, sünek malzemelerde akma dayanımı, gevrek malzemelerde ise çekme dayanımı
olabilir.
Eğme deneylerinde iki ucundan mesnetlenmiş (basit kiriş) dikdörtgen veya dairesel kesitli çubuk veya
kiriş numuneler kullanılır. Aşağıdaki şekilde görüldüğü gibi; orta noktasında düşey yönde etkiyen P
kuvvetinin doğurduğu eğilme momenti kiriş kesitinde yayılı normal gerimeler oluşturur. Başlangıçta
düşük yükler altında gerilmelerin yayılışı lineerdir. Kirişin en alt lifinde (+σm ) en büyük çekme gerilmesi,
üst lifinde (-σm) en büyük basınç gerilmesi oluşur. Kesitte, düşey doğrultuda gerilmelerin yön
değiştirdiği (çekme-basınç) noktadan boyuna yönde geçen tarafsız eksen üzerinde normal gerilmeler
(basınç veya çekme) sıfır, kesme gerilmeleri ise maksimum olur. Kesit yüksekliğince tarafsız
eksenden daha uzaktaki liflerde daha büyük basınç veya çekme gerilmeleri oluşur. Nitekim en büyük
gerilmeler kesit üst ve alt kenarında olur. Bu gerilmelerin dağılışı, malzemenin lineer elastik davranış
bölgesinde şekil (b)’deki gibi lineer, akma sınırından sonra şekil (c)’deki gibi eğriseldir.
Deneyin yapıldığı basit kiriş durumunda bu tarafsız eksenin numune kesit yüksekliğinin tam ortasında
(h/2) olduğu kabulüyle, alt kenar üzerindeki en büyük çekme veya üst kenar üzerindeki en büyük
basınç gerilmeleri aşağıdaki bağıntılar yardımıyla hesaplanabilir.
46
MALZEME BİLİMİ
Basınç, Kesme ve Eğilme Etkisinde Davranış
Tek (yada üç) noktalı eğilme deneyi
Sünek malzemelerde (σm ) gerilmesi akma sınırı (σ A)’ya eşit olunca akma başlar, gerilme yayılışının
lineerliği bozulur ve şekil (c)’deki eğrisel biçimi alır. Bu bölgede Hooke kuralı geçersizdir, gerilme
hesapları için yukarıdaki denklem kullanılamaz. Kesitin basınç veya çekme bölgesinde oluşan gerilme
bloku eşdeğer kuvvetinin tarafsız eksene göre momenti alınıp dış kuvvetin oluşturduğu momente
eşitlenerek dış lifleri zorlayan maksimum gerilmeler elde edilebilir.
Gevrek malzemelerde genellikle kırılma oluncaya kadar lineer elastik davranış geçerlidir. Bu durumda
kirişi kırmak için uygulanan (Pk) kırma kuvveti ölçülür ve yukarıdaki denklemde yerine koyarak kırmayı
oluşturan maksimum çekme gerilmesi elde edilir. Bu gerilme malzemenin çekme mukavemetine
oldukça yakındır, ancak doğrudan çekme mukavemeti sayılmaz, uygulamada “Eğilmede Çekme
Dayanımı” olarak adlandırılır.
Betonun eğilmede çekme dayanımı tayini, yukarıdaki gibi tek noktadan yükleme yapılabildiği gibi,
numune mesnet açıklığının L/3’lik eşit noktalarında bulunan 2 noktadan yükleme şeklinde de
yapılabilir.
47
MALZEME BİLİMİ
Basınç, Kesme ve Eğilme Etkisinde Davranış
İki (yada dört) noktalı eğilme deneyi
Özelikle beton ve ahşap numunelere uygulanan iki noktalı eğilme deneyinde elde edilen eğilme
dayanımı tek noktalı eğilme deneyinde elde edilen eğilme dayanımından biraz daha küçük olduğu
gözlenmiştir. Öğle ki, tek noktalı eğilmede maksimum eğilme momenti ve maksimum çekme gerilmesi
yalnız kuvvetin altındaki tek bir kesitte oluşur, oysa iki noktalı eğilmede maksimum moment ve çekme
gerilmesi açıklık ortasındaki L/3’lük bir uzunluk boyunca geniş bir alanda etkili olduğundan, kırılmaya
neden olacak kritik kusurun bulunma olasılığı daha büyüktür ve dolayısıyla daha düşük bir gerilme
kırılma oluşturabilir. uygulama yönünden iki noktalı eğilme deneyi sonuçları daha güvenilir sayılır.
Eğme etkisinde malzemenin şekil değiştirmeye karşı direnci veya eğilme rijitliği kirişin orta noktasında
oluşan (f) çökmesini (sehim) ölçerek saptanabilir. Eğme rijitliği malzemenin (E) elastisite modülü ile
doğru, (f) çökmesi ile ters orantılıdır. Nitekim eğilme deneyi sonuçlarından yararlanarak aşağıdaki
bağıntı ile elastisite modülü hesaplanabilir;
Eğilme deneyleri genellikle gevrek malzemelere uygulanır, deney düzeneği basit olmakla beraber
kolay uygulanır ve az bir kuvvetle parça kırılır. Bu tür malzemelere çekme deneyi uygulamak oldukça
zordur. Bu nedenle betonun çekme dayanımı için direkt çekme deneyi yerine eğilmede çekme veya
silindir numunelere uygulanan yarmada çekme deneyleri yaygın şekilde kullanılır.
48
MALZEME BİLİMİ
Basınç, Kesme ve Eğilme Etkisinde Davranış
KAYNAKLAR
1.
2.
3.
4.
Malzeme Bilimi, Kâşif Onaran, Bilim Teknik Yayınevi, 2009.
İnşaat Mühendisleri için Malzeme Bilgisi, Bülent Baradan, Dokuz Eylül Üniversitesi, 2003.
Malzeme Bilgisi ve Muayenesi, Temel Savaşkan, Karadeniz Teknik Üniversitesi, 2004.
Malzeme Bilgisi Ders Notları, Hayri Ün, Pamukkale Üniversitesi
49