2
Elektrik Akımı Test Çözümleri
1
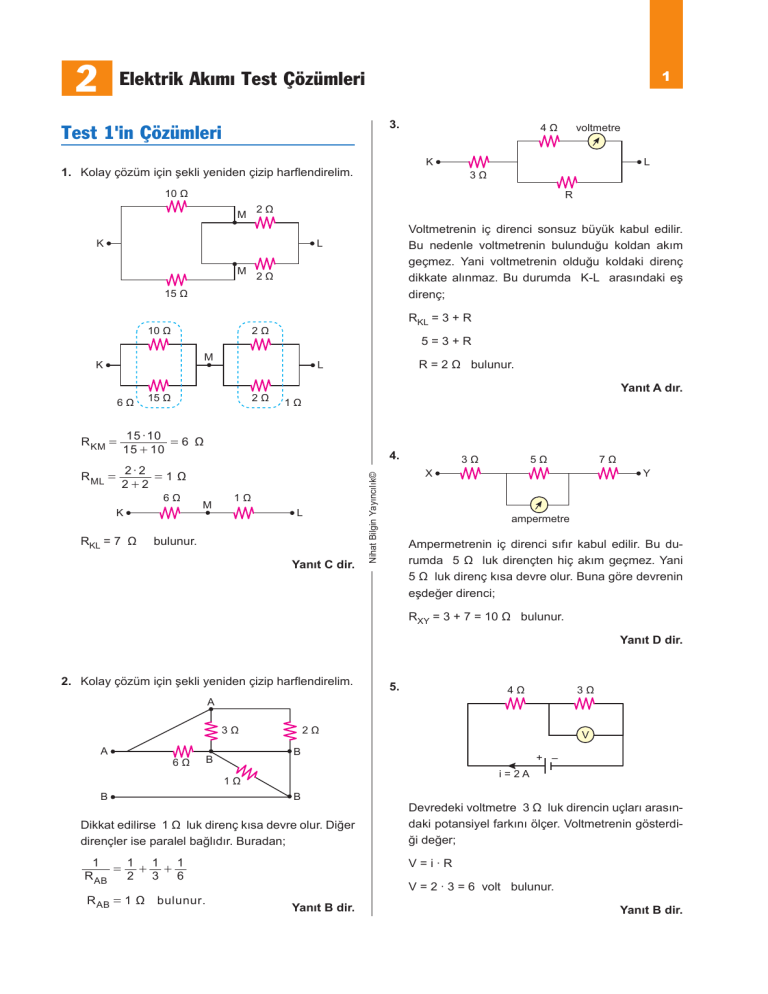
3.
Test 1'in Çözümleri
4Ω
K
1. Kolay çözüm için şekli yeniden çizip harflendirelim.
L
3Ω
10 Ω
R
M
2Ω
K
L
M
2Ω
15 Ω
10 Ω
K
L
2Ω
R KM =
2·2
R ML =
=1Ω
2+2
6Ω
RKL = 7 Ω
R = 2 Ω bulunur.
4.
M
1Ω
K
5=3+R
Yanıt A dır.
15 · 10
=6 Ω
15 + 10
1Ω
L
bulunur.
Yanıt C dir.
Nihat Bilgin Yayıncılık©
15 Ω
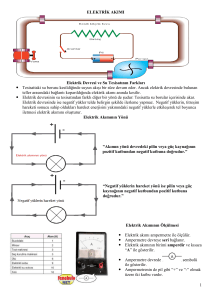
Voltmetrenin iç direnci sonsuz büyük kabul edilir.
Bu nedenle voltmetrenin bulunduğu koldan akım
geçmez. Yani voltmetrenin olduğu koldaki direnç
dikkate alınmaz. Bu durumda K-L arasındaki eş
direnç;
RKL = 3 + R
2Ω
M
6Ω
voltmetre
3Ω
5Ω
7Ω
X
Y
ampermetre
Ampermetrenin iç direnci sıfır kabul edilir. Bu durumda 5 Ω luk dirençten hiç akım geçmez. Yani
5 Ω luk direnç kısa devre olur. Buna göre devrenin
eşdeğer direnci;
RXY = 3 + 7 = 10 Ω bulunur.
Yanıt D dir.
2. Kolay çözüm için şekli yeniden çizip harflendirelim.
5.
4Ω
3Ω
A
3Ω
A
2Ω
V
B
6Ω
+ –
B
i=2A
1Ω
B
B
Devredeki voltmetre 3 Ω luk direncin uçları arasındaki potansiyel farkını ölçer. Voltmetrenin gösterdiği değer;
V=i·R
V = 2 · 3 = 6 volt bulunur.
Dikkat edilirse 1 Ω luk direnç kısa devre olur. Diğer
dirençler ise paralel bağlıdır. Buradan;
1
1 1 1
= + +
R AB
2 3 6
R AB = 1 Ω
bulunur .
Yanıt B dir.
Yanıt B dir.
2
ELEKTRİK AKIMI
6. Voltmetrenin iç direnci sonsuz büyük olduğundan
voltmetrenin üzerinden akım geçmez. Bu nedenle
soru çözümlerinde önce voltmetre devrede yokmuş
gibi düşünebiliriz.
7. Voltmetrenin direnci sonsuz olduğu için soru çözümlerinde voltmetreleri kaldırabiliriz.
K
2R
R
L
M
3R
N
3Ω
K
i
M
i2
+ –
2Ω
6Ω
L
K
M
i1
i
+ –
K
V1 voltmetresi K-M arasına bağlı olduğu için bu
noktalar arasındaki potansiyel farkını ölçer.
M
24 volt
Şekildeki dirençler seri olduğu için hepsinden aynı i
akımı geçer.
V1 = i · RKM
K-M noktaları arasındaki potansiyel farkı 24 volt olduğundan;
V1 = i · (2R + R)
V = i · RKM
V1 = 3iR
24 = i1 · (2 + 6)
V2 voltmetresi L-N arasına bağlı olduğu için bu
noktalar arasındaki potansiyel farkını ölçer.
i1 = 3 amper bulunur.
V2 = i · RLN
Nihat Bilgin Yayıncılık©
3Ω
V
6Ω
K
L
2Ω
i
+
–
24 volt
Voltmetre K-L noktaları arasındaki potansiyel farkını ölçer. Buna göre;
VKL = i1 · RKL
VKL = 3 · 2 = 6 volt
bulunur.
Yanıt A dır.
V2 = i · (R + 3R)
V2 = 4iR
Bu durumda
V1
V2
=
3
4
bulunur.
Yanıt D dir.
3
ELEKTRİK AKIMI
8.
10.Voltmetrenin direnci sonsuz kabul edilir. Bu nedenle voltmetrenin olduğu koldan akım geçmez.
2A K 7A
2A
2A
3A
i2
i2
L
i1
+ –
anahtar
K noktasına gelen akımlar, çıkan akımlara eşit olmalıdır. Buna göre;
i2 + 2 = 7
olur. L noktasına gelen akımlar, çıkan akımlara eşit
olmalıdır. Buna göre, i1 = 2 A olacaktır. Buradan;
i1
2
=
5
i2
3Ω
V
2Ω
A
i + –
10 volt
Bu durumda voltmetrenin üretecin uçlarına bağlı olduğunu düşünebiliriz.
Yani voltmetre 10 voltluk değer gösterir.
Ampermetrenin gösterdiği değer ise;
V=i·R
10 = i · 2
i=5 A
bulunur.
Yanıt A dır.
bulunur.
Yanıt E dir.
Nihat Bilgin Yayıncılık©
i2 = 5 A
Ampermetrenin direnci
sıfır kabul edilir. Bu yüzden 3 Ω luk dirençten
hiç akım geçmez. Akımın tamamı ampermetrenin olduğu koldan geçer.
11.
X
R
Y
2i1
K
i2
R
R
L
M
R
M
R
i1
9.
R
+ –
2i2
i1
+ –
Y direncinden 2i kadar akım geçiyor olsun. Bu durumda i1 = i ve i2 = 3i olur. Ohm Kanununa göre;
VLM = 2i · R = 2 volt ise
i2
2R
R ve 2R dirençleri birbirine paralel bağlıdır. Bu nedenle 2R direncinden i2 akımı geçerse R direncinden 2i2 akımı geçer. Bu durumda i1 = 3i2 olur.
i1
Buradan,
= 3 bulunur.
i2
Yanıt C dir.
VKL = 3i · R = 3 volt olur.
Buna göre;
VKM = VKL + VLM
VKM = 5 volt
bulunur. X direnci K-M noktalarına bağlı olduğu için
X direncinin uçları arasındaki potansiyel farkı 5 volt
olur.
Yanıt A dır.
4
ELEKTRİK AKIMI
14.Ampermetrenin iç direnci sıfır kabul edilir. Bu durumda devre aşağıdaki gibi çizilebilir.
,
12.Bir iletkenin direnci R = t ·
dır. Ayrıca Ohm KaA
V
nununa göre R =
dir. Bu iki bağıntı eşitlenip
i
özdirenç yalnız bırakılırsa;
t
4i
2R
, =V
A
5i
i
8i
t=
A
,
·
R
9i
R
3R
3i
V
i
+ –
metre 2
volt
t=
·
metre amper
t=
metre · volt
amper
Yanıt A dır.
bulunur .
K
R
R
R
K
L
K
R
R
K
8A
+ –
K
12i = 12 A olur.
Yanıt E dir.
15.Şekildeki dirençler birbirine paralel bağlıdır. Bu nedenle 3R direncinden i2 akımı geçerse R direncinden 3i2 akımı geçer.
3R
24 volt
Ohm Kanununa göre;
V = i · Reş
R
24 = 8 ·
3
R = 9 Ω bulunur.
L
5i = 5 A ise
Nihat Bilgin Yayıncılık©
13.Şekil incelendiğinde sol taraftaki dirençlerin kısa
devre olduğu, sağ taraftaki dirençlerin de birbirine
paralel olduğu görülür. Devreyi aşağıdaki gibi yeniden çizelim.
3R direncinden 3i akımı geçerse R direncinden
9i akımı geçer. Çünkü paralel bağlı dirençlerde
akım dirençle ters orantılıdır. Bu durumda 2R direncinden 4i akımı geçer. Buna göre, A1 ampermetresinin bulunduğu koldan 5i, A ampermetresinden de 12i akımı geçer.
R
3R
R
K
i2
i2
R
L
3i2
+ –
R
8A
i1
+ –
24 volt
Yanıt C dir.
Buna göre;
i1 = i2 + i2 + 3i2
i1 = 5i2
i1
i2
=5
bulunur.
Yanıt A dır.
5
ELEKTRİK AKIMI
3. Devreleri besleyen üreteçlerin potansiyel farkı V
olsun.
Test 2'nin Çözümleri
1.
(1)
+
+2q
+
– 4q
–
A
Şekil I deki devre elemanlarının
hepsi birbirine paralel bağlı olduğu için uçları arasındaki potansiyel farkları eşit olup V kadardır.
K
V
+ –
V
+ –
V
Şekil I
–4q yükünün (2) yönünde gitmesi +4q yükünün
(1) yönünde gitmesi gibi etki yapar. Buna göre;
yük
Akım şiddeti = zaman
2q + 4q
6q
i=
=
t
t
bulunur.
Yanıt C dir.
2.
i1
Şekil II deki dirençler birbi-
rine seri bağlıdır. Her bir di1
rence
V potansiyel farkı
2
V
düşer.
L
+
Bir iletkenin kesitinden birim zamanda geçen yük
miktarına akım şiddeti denir. Akım şiddetinin yönü
pozitif yüklerin hareket yönü olarak kabul edilir. Bu
durumda akım şiddeti (1) yönünde olmalıdır.
–
V
—
2
V
—
2
Şekil II
Yanıt D dir.
Nihat Bilgin Yayıncılık©
R1
R3
i
R2
4. Bir dirençten geçen akım ile direnç ters orantılıdır.
i2
3i
R1 ve R2 dirençlerinin uçları arasındaki potansiyel
farkları birbirine eşittir. Küçük dirençten çok akım
geçeceğinden R1 > R2 olur. I. yargı yanlıştır.
L
2i
+ –
Verilen bilgilerle R2 ve R3 dirençlerini karşılaştıramayız. Bu nedenle II. yargının doğruluğu kesinlik
taşımaz.
K
i
M
+ –
i = i1 + i2 olduğundan III. yargı kesinlikle doğrudur.
M direncinden i akımı geçerse L direncinden 2i
akımı geçer. Bu durumda K direncinden 3i akımı
geçer.
Yanıt C dir.
Yanıt A dır.
6
ELEKTRİK AKIMI
5.
7. Şekildeki gibi harflendirme yapalım.
+ –
K
+
i1
R1 = R
R2
R1
R2 = R
/
/
R3
L
K
i·R
V = i1 · R1
Aynı kuralı devrenin en dışına uygularsak;
/ V = / i·R
L
– +
Kirşof'un 2. kuralını üstteki kapalı devreye uygulayalım.
V=
–
L
K
i2
K
Dikkat edilirse tüm dirençlerin bir ucu K noktasına
öteki ucu da L noktasına bağlıdır. Buna göre, dirençlerin tümü birbirine paralel bağlıdır. Birbirine
paralel bağlı özdeş dirençlerden geçen akım şiddetleri eşit olur.
Yanıt E dir.
V + V = i2 · R2
2V = i2 · R2
bulunur .
Nihat Bilgin Yayıncılık©
Yanıt D dir.
6.R1 = R2 = R3 = R, V1 = V2 = V alalım.
R2 = R
i2
R
—
2
i1 R1 = R
8. Şeklimizi aşağıdaki gibi yeniden çizebiliriz.
i1 = 3 A
R
2V
—–
3
V
R1 = 4 Ω
V
—
3
+ –
V1 = V
Üreteçlerin potansiyeli dirençlere, şekildeki gibi bölüşülür.
2V
3
2V
i1 =
=
R
3R
V
3
V
i2 =
=
R
3R
V
2
V
i3 =
=
R
2R
i1 > i3 > i2
i3
V
—
2
V
—
2
+ –
V2 = V
Yanıt C dir.
i2 = 1 A
R2 = 12 Ω
i3 = 4 A
R3 = 3 Ω
Direnci R1 = 4 Ω olan koldan i1 = 3 A lik akım geçerse, direnci R2 = 12 Ω olan koldan i2 = 1 A lik
akım geçer. Voltmetrenin iç direnci sonsuz büyük
olduğunan voltmetrenin bulunduğu koldan akım
geçmez. Bu nedenle R3 = 3 Ω luk dirençten;
i3 = i1 + i2 = 4 A
lik akım geçer. Voltmetre R3 direncinin ucundaki
potansiyel farkını ölçeceği için;
V = i3 · R3
V = 4 · 3 = 12 volt
bulunur.
Yanıt C dir.
7
ELEKTRİK AKIMI
9.
11.
12 volt
2Ω
i1
6Ω
Y
X
i
Z
2A
3Ω
i
6Ω
1A
i
i2 = 1 A
6Ω
2A
3A
12 Ω
6Ω
Y-Z noktaları arasındaki potansiyel farkının 12 volt
olması için bu kollardan sırasıyla 2 A ve 1 A lik
akımların geçmesi gerekir. Bu durumda X-Y noktaları arasındaki 6 Ω luk dirençlerden de 1,5 A lik
akımlar geçer. Buradan;
VXY = 1,5 · 6 = 9 volt bulunur.
3Ω
Şekildeki devrede alt koldaki 6 Ω luk dirençten geçen akımın i2 = 1 A olduğunu varsayalım. Bu durumda 3 Ω luk paralel durumdaki dirençten geçen
akım 2 A olur. Böylece alt kolun tamamından 3 A
lik bir akım geçer.
Alt kolun eşdeğer direnci 5 Ω ve bu koldan 3 A lik
akım geçtiğine göre, bu kolun potansiyel farkı 15
volttur. üst kolun potansiyel farkının da 15 volt ol15
ması için 2 Ω luk dirençten i1 =
amperlik akım
2
geçmelidir. Buradan;
Yanıt B dir.
i1
Nihat Bilgin Yayıncılık©
i2
=
15
15
=
2
2
1
bulunur.
Yanıt E dir.
12.
– +
12 Ω
10.
3i
3R
2R
3Ω
5R
K
i1
1Ω
i2
R
9R
6R
L
i
15R
4Ω
Alt koldaki eşdeğer direnç 15R, üst koldaki eşdeğer direnç 5R dir. Bu nedenle alt koldan i akımı
geçerse üst koldan 3i akımı geçer. V1 , V2 voltmetrelerinin gösterdiği değerler;
V1 = 3i · 3R = 9iR
V2 = i · 6R
olur. Bu durumda 2V1 = 3V2 dir.
Yanıt A dır.
Devreden geçen i1 ve i2 akımlarının eşit olması
için akımların geçtiği kolların dirençlerinin eşit olması gerekir.
Alt koldaki direnç 4 Ω olduğuna göre orta koldaki
dirençlerin eşdeğeri de 4 Ω olmalıdır.
K direnci 1 Ω ise kesikli çizgi içine alınan kısım 3
Ω olmalıdır. Bu nedenle R = 4 Ω olur.
Yanıt B dir.
8
ELEKTRİK AKIMI
13.
15.
R
V3
R2
V1
X
i
K
Y
R1
i
i1
R3
i2
R5
i3
R
2i
R
3
R
2
R
R4
V5
K direncinden geçen akım şiddeti i ise alt koldan
3
2i akımı geçer. Alt kolun eşdeğer direnci
R ol2
duğundan bu kolun potansiyel farkı;
i3 anakol akımı olduğundan hem i1 den hem de i2
den büyüktür. i1 = i3 olamaz.
Yanıt B dir.
3
R · 2 i = 3 iR
2
olur. iR = 1 volt ise 3iR = 3 volt bulunur. X-Y arasındaki potansiyel farkı da 3 volt olur.
Yanıt B dir.
14.
2
A
A
A
i1
2A
i2
r=0
r=0
+ –
+ –
V
V
Şekil I
Şekil II
Uzunluğu , , kesit alanı A olan bir iletkenin direnci;
R=t
2R
R
2
r=0
i1 =
V
V
V
2V
=
1
R
R
2
2V
– +
i2 =
3V
– +
C
D
+ –
B
3V
– + 3V
r=0
+ –
3V 6V
+ –
VAB = 4V olur.
2R
3
R
i2
3V
+ –
Potansiyel farkı 3V olan iki üreteç seri bağlı olup
bu iki üretecin toplam potansiyel farkı 6V dir. Potansiyel farkı 2V olan diğer üreteç, potansiyel farkı
6V olan üretece ters bağlıdır. Bu nedenle;
R
R
i1
2V
– +
A
,
R
16.
A
bağıntısıyla bulunur. Metaller aynı cins olduğuna
göre t lar aynıdır. Buna göre uzunluğu ,, kesit
alanı A olan iletkenin direncini R alarak devreleri
aşağıdaki gibi yeniden çizelim.
Nihat Bilgin Yayıncılık©
2
A
Potansiyel farkı 3V olan iki üreteç birbirine paralel
bağlı olduğundan bu iki üretecin toplam potansiyel
farkı yine 3V olur. 2V lik üreteç ile 3V lik üreteç
seri bağlı olduğundan;
VCD = 5V
3V
V
=
5
5R
R
3
i1
2V 5R
=
·
i2
R
3
VCD
VAB
=
5
4
bulunur.
Yanıt E dir.
Yanıt E dir.
9
ELEKTRİK AKIMI
3.
Test 3'ün Çözümleri
1.
V
– +
L
4
– +
M
2
4
1
N
L
3
2
M
1
K
3
K
L lambasının sönmesi için 1 numaralı anahtar kapatılmalıdır.
M lambasından akım geçmesi için
anahtar kapatılmalıdır.
K lambasının ışık vermesini istemediğimiz için 3 numaralı anahtarın açık kalması gerekir.
Akımın N lambasından geçmesi için 4 numaralı
anahtarın açık olması gerekir.
2 ve 3 numaralı anahtarlar kapatılırsa yalnız K lambası ışık verir.
Yanıt B dir
2 numaralı
3
Z
i
2
1
4
X
Y
+
Nihat Bilgin Yayıncılık©
Yanıt B dir.
4.
–
5
Yalnızca 3 numaralı anahtarı kapatırsak yalnız Y
lambası ışık verir.
Yanıt B dir.
2.
– +
Y
A2
K
X
A1
L
A1 açık, A2 kapalıyken K lambası kısa devre olmaktadır. A1 kapatılıp A2 açıldığında L lambası kısa devre olmaktadır. Her iki durumda da X ve
Y lambalarına düşen gerilim değişmez. Bu nedenle her iki lambanın parlaklığı değişmez.
Yanıt C dir.
5. Anahtar ister açık
olsun ister kapalı olsun her durumda N
ve L lambaları kısa
devre olur. Anahtarların her konumunda
ışık veren lamba M
lambasıdır.
V
– +
N
M
L
K
Yanıt B dir.
10
ELEKTRİK AKIMI
6.
+
8.
–
K
X
K
P
A1
L
Y
Z
A2
A3
X
N
+ –
M
Anahtarların açık ya da kapalı olması durumları şekillerdeki gibidir. Her iki şekilde de akım K, M ve X
lambalarından geçer.
+
–
K
II. A3 anahtarı kapatıldığında üreteç kısa devre
olur. Bu durumda devredeki lambalar ışık vermez.
L
III. A1 anahtarı açıldığında X, P ve Y lambalarından oluşan kısmın direnci artar. Böylece bu
kısma düşen gerilim de artar. Gerilim artarsa
lambaların parlaklıkları da artar.
X
M
Yanıt D dir.
Nihat Bilgin Yayıncılık©
N
I. Z lambası devreye seri bağlıdır. Bu nedenle
A2 anahtarı kapatılırsa Z lambası kısa devre
olacağından X ve Y lambalarına düşen gerilim
artar. Bunun sonucunda X ve Y lambalarının
parlalığı artar.
Yanıt C dir.
9.
7.
V
3V
+ –
+ –
+ –
+ –
+ –
+ –
+ –
+ –
+ –
V
+ –
K
L
2V
i1
+ –
+ –
V
2V
Üreteçlerin gerilimleri dağı-
tıldığında K lambasının gerilimi V, L ninki 2V, M ninki
V dir. Buna göre lambaların
parlaklık sırası L > K = M
biçimindedir.
V
R
+ –
+ –
i2
M
i1 =
V
1
i2 =
= i
R
3
+ –
+ –
3V
Yanıt A dır.
V
3V
= i ise
R
V
R
Şekil II
Şekil I
V
– +
i3 =
V
1
= i
R
3
i3
R
Şekil III
Yanıt A dır.
11
ELEKTRİK AKIMI
10.
12.
V
– +
Y
Y
Y
X
X
r=0
M
K
N
i1
X
i2
A
B
+ –
+ –
L
V
X
X
Şekil II
X
Üretecin bir ucu X, diğer ucu Y olsun. N lambasının da bir ucu X, öteki ucu Y dir. Bir başka ifadeyle, N lambası üretece paralel bağlıdır. Anahtar ister
açık olsun ister kapalı olsun bu durum değişmez.
Bu nedenle N lambasının gerilimi her iki durumda
da V olup parlaklığı değişmez.
Özdeş lambalardan birinin direnci R olsun. Bu durumda Şekil I deki eşdeğer direnç 2R, Şekil II deki
R
olur. Devrelerin anakol akımları;
2
i1 =
Buna göre Şekil I deki lambalardan i akımı geçerse Şekil II deki her bir lambadan 2i akımı geçer.
Geçen akımın büyüklüğüne göre, Y lambasının
ışık şiddeti X inkinden daha büyüktür.
Üreteçlerin ömrü, devreye sağladıkları akımın büyüklüğüyle ters orantılıdır. A üreteci devreye i akımı sağlıyorken, B üreteci 4i akımı sağlıyor. Buna
göre A üretecinin ömrü B ninkinden uzundur.
Nihat Bilgin Yayıncılık©
Yanıt B dir.
11.
–
V
Şekil I
A2
+
–
+
A1
–
+
V
=i
2R
V
ise i 2 =
= 4i
R
2
Yanıt C dir.
13.Şekil I de kısa devreden
dolayı M lambası ışık L
vermez. K ve L lambaları
eşit şiddette ışık verir.
+
–
Vtop = 0
L
K
M
+
K
Şekil I
M
K
A3
+
i
–
i
–
+
2i
–
+
V
2V
L
L
i
i
V
+
+
+
M
–
–
V
M
–
olur.
–
2i
A1 anahtarı kapatıldığında kısa devreden dolayı K
lambası ışık vermez. A2 anahtarı kapatıldığında
ters bağlamadan dolayı bu devrede toplam gerilim
sıfır olur. Bu nedenle L lambası ışık vermez. A3
anahtarı kapatıldığında M lambası ışık verir.
Yanıt A dır.
Şekil II
K
Şekil III
Şekil II ve Şekil III te görüldüğü gibi K lambası ana
kol üzerindedir. L ve M lambalarından i akımı geçtiğinde K lambasından 2i akımı geçer ve bu lamba diğer ikisinden daha şiddetli ışık verir.
Yanıt A dır.
12
ELEKTRİK AKIMI
14.X lambası üretece paralel bağlıdır. Anahtar açık
da olsa kapalı da olsa X
lambasının gerilimi V kadardır. Bu nedenle anahtar kapatıldığında X lambasının
parlaklığı
değişmez.
II. Anahtarların kapatılmasıyla önceki üretece
paralel olarak yeni bir üreteç daha devreye
girer. Bu da L üretecinin ömrünü uzatır.
X
V
, Şekil II de
2
V
olduğundan M lambasının ışık şiddeti azalır.
3
Yanıt E dir.
III. Şekil I de M lambasının gerilimi
K
r=0
+ –
V
Anahtar
kapatıldığında
paralel bir lamba daha devreye gireceğinden eşdeğer direnç önceki duruma göre küçülür. Eşdeğer
direncin küçülmesi sonucu üreteçten çekilen akım
miktarı artar. Üreteçlerin ömrü, devreye verdikleri
akımın şiddetiyle ters orantılıdır. Akım şiddeti artınca üretecin ömrü azalır.
15.Her iki anahtar açık iken devre Şekil I deki gibidir.
Her iki anahtar kapalıyken devre Şekil II deki gibidir.
V
– +
L
Şekil I
V
2
V
2
K
Nihat Bilgin Yayıncılık©
Yanıt B dir.
16.Şekilde I deki paralel diR
rençlerin eşdeğeri
seri
2
üreteçlerin eşdeğeri 2V olduğundan;
V
– +
L
Şekil II
2V
V
olur.
=4
R
R
2
V
3
2V
3
I. Şekil I deki devrede üretecin V olan gerilimi K
V
ve L lambaları arasında
şer olarak payla2
şılır. Şekil II deki devrede K lambasına düşen
2V
gerilim
olur. Bu nedenle her iki anahtar
3
birlikte kapatıldığında K lambasının ışık şiddeti
artar.
+ –
+ –
V
V
2V
Şekil II de iki seri di2R
R
R
rencin eşdeğeri 2R,
iki paralel üretecin eş- 2i
2
+ –
değeri V dir. Ayrıca
i2
akımın geçtiği yere
V
i2
dikkat edilirse
ana
+ –
koldan geçen akım 2i2
V
V
olur. Buradan;
V
2i2 =
2R
i2 =
i1
Şekil II
K
M
R
Şekil I
M
– +
i1 =
R
2
R
V
4R
bulunur .
Şekil III te eşdeğer direnç 2R, eşdeğer gerilim
2V olduğundan;
2V
V
i3 =
=
2R
R
bulunur. Buna göre;
R
R
2R
i3
+ –
+ –
V
V
2V
Şekil III
i1 > i3 > i2 dir.
Yanıt C dir.
ELEKTRİK AKIMI
2.
Test 4'ün Çözümleri
1. Anahtar açık iken devre Şekil I deki gibi, anahtar
kapatılınca devre Şekil II deki gibidir.
V
2
13
V
+ –
V
+ –
10 volt
V 15 volt
+ –
V
– +
V
+ –
V
+ –
V
+ –
V
2
15 volt
K
M
R = 10 Ω
R
Şekil I
R
i1
+ –
En sağdaki üreteç diğerlerine ters bağlıdır. Bu nedenle tüm devrenin toplam gerilimi 10 volttur. Buna
göre, direnci 10 Ω olan lambanın gücü;
P=
V2
R
P=
10 2
= 10 watt bulunur .
10
V
V
3
2V
3
R
2
K
Yanıt B dir.
M
Şekil II
L
R
S
i2
V
V
V
değerini, Şekil II de
2
3
değerini ölçer. Şekil I de eşdeğer direnç 2R, Şekil
3
II de R dir. Buna göre;
2
Şekil I de voltmetre
V
i1 =
2R
V
2V
i2 =
=
3
3R
R
2
Nihat Bilgin Yayıncılık©
+ –
3.A1 anahtarı kapalı, A2 anahtarı açık iken devre
Şekil I deki gibidir. A2 kapatılıp A1 açılınca devre
Şekil II deki gibi olur.
V2
– +
L
A1
K
Şekil I
i1
V1
– +
A2
olup, i2 > i1 dir.
V2
– +
Yanıt D dir.
Şekil II
K
i2
Şekil II de birbirine seri bağlı iki üreteç devreye akım
verir. K lambasına daha önce yalnızca V2 gerilimi
düşerken Şekil II de V1 + V2 gerilimi düşer. Yani K
lambasının ışık şiddeti artar. I. yargı doğrudur.
i2 > i1 olduğundan potansiyel farkı V2 olan üretecin ömrü öncekine göre kısalır. II. yargı doğrudur.
Şekil II de L lambası ışık vermez. III. yargı yanlıştır.
Yanıt C dir.
14
ELEKTRİK AKIMI
4.
X
Y
6.
Z
B
K
A
A
A
+ –
A
L
A
+ –
B
A
A
M
+ –
Bütün lambaların ve üretecin (+) ucu A noktasına,
diğer uçları da B noktasına bağlıdır. Buna göre lambaların tamamı üretece paralel bağlı olup ışık şiddetleri eşittir.
L lambasının iki ucu da A noktasına bağlı olduğu
için bu lamba kısa devre olur ve ışık vermez. K ve
M lambaları ise ışık verir.
5.
K
L
V
–
–
+
–
V
V
+
3V
2V
K lambasının uçları
M
arasındaki potansiyel
farkı 2V dir. L lambaV –
sının uçları arasındaV
V
–
ki potansiyel farkı 3V
V
dir. Şekil III te üreteç+ –
lerden biri ters bağlı
ters bağl
olduğu için M lambasının uçları arasındaki potansiyel farkı V olur.
7.
X
Y
+
V
+
–
–
+
–
+
V
V
+
V
Yanıt E dir.
Nihat Bilgin Yayıncılık©
Yanıt D dir.
reosta
+
Özdeş lambaların ışık şiddetleri uçları arasındaki
potansiyel farkıyla doğru orantılıdır. Bu nedenle;
IL > IK > IM olur.
Yanıt A dır.
+ –
X lambası üretece paralel bağlı olduğu için bu lambanın parlaklığı değişmez.
Reostanın sürgüsü ok yönünde çekildiğinde Y lambasının bulunduğu kolun direnci azalır. Bu durumda
bu koldan geçen akım şiddeti artar. Böylece Y lambasının parlaklığı artar.
Yanıt D dir.
15
ELEKTRİK AKIMI
8.
10.
K
A
ters bağl
9V
+ –
+ –
1,5V
9V
+ –
– +
3V
+ –
+
+
L
4,5V
12V
3V
–
–
M
B
El feneri 12 voltluk gerilimle çalıştığı için pilerin eşdeğer gerilimi 12 volt olmalıdır.
Devreyi aşağıdaki gibi yeniden çizelim.
Yanıt B dir.
L
B
A
K
2i
– +
11.Bağımsız değişken, deney sırasında bizim bilinçli
olarak değiştirdiğimiz değişkendir. Bu deneyde iletkenin cinsi bağımsız değişkendir.
i
M
– +
i
Bu durumda K ve M lambalarında i akımı geçerse L lambasından 2i akımı geçer. Yani lambaların
ışık şiddetleri arasındaki ilişki IL > IK = IM olur.
Yanıt A dır.
Nihat Bilgin Yayıncılık©
V
bakr
A3
demir
A2
gümüş
A1
Bağımlı değişken, bağım+ –
sız değişkene bağlı olarak
değişen değişkene denir.
Bu deneyde ampermetrede okunan akım şiddeti
bağımlı değişkendir.
Kontrollü değişken, deneyde sabit tutulan değişkendir. Bu deneyde kontrollü değişken iletkenlerin
boyu ve kesit alanıdır.
Yanıt B dir.
9.
P
R
N
2i
12.
i
M
i
2i
3i
i
S
+ –
L
+
R lambasından i akımı geçerse N lambasından
2i akımı geçer. Bu durumda S lambasından da 3i
akımı geçer.
Özdeş lambaların parlaklığı üzerlerinden geçen
akım şiddetiyle doğru orantılı olduğundan lambaların ışık şiddetleri arasında IP = IR < IS ilişkisi bulunur.
Yanıt E dir.
–
K
+ –
+ –
K lambasından i akımı geçerse L lambasından
da i akımı geçer. Bu durumda M lambasından 2i
akımı geçer. Özdeş lambaların ışık şiddetleri lambadan geçen akım şiddeti ile doğru orantılıdır. Buna
göre IK = IL < IM olur.
Yanıt C dir.
16
ELEKTRİK AKIMI
13.
14.
3
M
R
V
K
Z
X
1
Y
A
V
2
–
r=0
+
L
P
A
4
Ampermetreler, akım şiddetinin ölçüleceği yere seri
bağlanır. İç dirençleri önemsenmeyecek kadar küçük olduğundan bağlandığı kolda ek bir direnç oluşturmaz.
Voltmetreler potansiyel farkının ölçüleceği iki nokta
arasına paralel bağlanır. Voltmetrelerin iç dirençleri
çok büyüktür. Bu nedenle elektrik devrelerine bağlandıklarında üzerlerinden akım geçmez.
Başlangıçta tüm lambalar ışık vermektedir. Ölçü
aletleri bağlandıktan sonra Y lambası artık ışık vermediğine göre 2 numaralı ölçüm aracı voltmetredir.
O hâlde 1 ve 4 numaralı ölçüm araçları ampermetre, 2 ve 3 numaralı ölçüm araçları ise voltmetredir.
Yanıt C dir.
Reostanın sürgüsü ok yönünde kaydırılırsa, şekildeki R direnci büyür. Bu da, R direncine seri bağlı L
ve M lambalarına düşen gerilimin azalması demektir.
K lambası üretece paralel bağlı ve üretecin iç direnci önemsiz olduğundan, K nın gerilimi reostanın hareketinden etkilenmez.
Yanıt D dir.
Nihat Bilgin Yayıncılık©
V