İNTEGRAL ALMA KURALLARI
Çözüm
5
ÖRNEK
ı
f (x) = 4x + 1 ise bu türev fonksiyonu integre edilirse
f(x) bulunur.
a ∈ Z+ olmak üzere
ı
xadx ve f (2) = 4 ise
f(x) =
ı
f (x)dx =
f(x) =
(4x + 1)dx =
a kaçtır?
f(x) = 2x2 + x + c
Çözüm
f(x) =
4x2
+x+c
2
f(0) = 5
xadx
ise
c = 5 olmalıdır.
O halde
f(x) = 2x2 + x + 5
bulunur.
ı
ı
f (x) =
xadx
ı
f (x) = xa
bulunur.
8
ÖRNEK
ı
ı
f (2) = 4 ise f (2) = 2a = 4
olduğundan a = 2 bulunur.
Her x reel sayısı için
dy
= 2xy
dx
f(x) =
ve f(1) = 1 olduğuna göre, y = f(x) fonksiyonu neye
eşittir?
6
ÖRNEK
(3x2 + 2x)dx
Çözüm
ve f(0) = 12 olduğuna göre f(1) kaçtır?
Çözüm
f(x) =
3 x 3 2x 2
+
+c
(3x2 + 2x)dx =
3
2
f(x) = x3 + x2 + c
f(0) = 0 + 0 + c = 12
ise
c = 12
dy
= 2xy
dx
ise
dy
= 2xdx dir.
y
Bu eşitliğin her iki tarafına integral alma işlemi uygulanırsa
dy
=
y
2xdx
Iny + c1 = x 2 + c 2
O halde
f(x) = x3 + x2 + 12 olur.
f(1) = 1 + 1 + 12 = 14 bulunur.
Iny = x 2 + c 2 − c1
C
Iny = x 2 + c
olur.
Buradan y yi yalnız bırakırsak;
ÖRNEK
7
2
f(x) = y = ex
+c
bulunur.
f(1) = 1 olduğuna göre,
ı
f (x) = 4x + 1, f(0) = 5
1 = e1+c ise c = –1 olmalıdır.
ise f(x) fonksiyonu neye eşittir?
O halde
2
f(x) = ex
12
–1
bulunur.
İntegral
İNTEGRAL ALMA KURALLARI
5.
y
ADIM GÜÇLENDİRME TESTİ-5
(ÇÖZÜMLÜ)
f(x)
d(e x .x )
x2
d + x
2
1. x
3
1
–1
işleminin sonucu nedir?
A) ex
B) exdx
C) xdx
D) x
E) 1
Yukarıdaki grafik 3. dereceden f(x) polinom fonksiyonuna aittir.
2. x +1
f(x) =
x x
x4
+ ax 3 + bx 2 + cx
4
f(x)dx =
olduğuna göre, 11a + 2b + c kaçtır?
dx
3
B) - 2
A) -9
C)
1
2
D) 2
5
2
E)
fonksiyonu veriliyor.
f(1) = 0 olduğuna göre, f(2) kaçtır?
A) -2
B) 0
C)
2
2
D)
2
E) 2 2
6. m ve n sıfırdan farklı reel sayılardır.
e2 x - 4 x
dx
e - (2e)x
3. f(x) =
sin (mx) dx +
fonksiyonu veriliyor.
π
f(0) = f = 2
n
cos (nx) dx
m
aşağıdakilerden hangisine eşit
olduğuna göre
n
olabilir?
2x
işleminin sonucu nedir?
x
2
B) x − + c e
A) x + ex + c
D) x +
C)
2x
x
e In2
+c
A) -2
1
B) - 2
E) 3
dx
x2
1+ 2
y
işleminin sonucu nedir?
cos2 x - 1
dx
sin4 x
A) sinx + c
B) –cosx + c
D) –cotx + c
32
3
2
2x
ex
+ c E) x −
+c
e ((In2) − 1)
(1− In2)
işleminin sonucu nedir?
1) A
D)
x
7. 4. C) 1
2) D
C)cotx + c
B) y.arctanx + c
x
C) y.arctan + c
y
x
D) 1 .arctan + c
y
y
E) tanx + c
3) D
A) arctanx + c
4) C
5) A
E) y.arctan(xy) + c
6) A
7) C
İntegral
BELİRLİ İNTEGRAL
ADIM
3
ÖRNEK
2
t2
d
dt
BELİRLİ İNTEGRALDE LEİBNİTZ TEOREMİ
0
x3 dx
dt işleminin sonucu nedir?
1
u(x)
f(x) =
h(t) dt
Çözüm
Öncelikle köşeli parantezin içindeki ifadeyi çözümleye-
v(x)
fonksiyonunun türevi Leibnitz Teoremine göre şu
şekilde hesaplanır.
lim.
t2
d
dt
d
(f ( x )) = f ′( x ) = u′( x ).h(u( x )) − v ′( x )h(v( x ))
dx
x3 dx
integralin t değişkenine bağlı türevi
1
sorulmakta. Leibnitz teoremini uygulayabiliriz.
t2
ADIM PEKİŞTİRME
1
ÖRNEK
x2
f(x) =
d
dt
t3
dt
t +1
ı
olduğuna göre, f (1) kaçtır?
0
Çözüm
f ′(1) =
0
1
2
x
f ′( x ) = 2x ⋅
= ( t 2 )′ .( t 2 )3 − (1)′
.(
1)3 = 2t.t6 = 2t7
Bulduğumuz bu sonucu soruda yerine yazalım.
2
f ′( x ) = ( x 2 )′
x3 dx
t2
d
dt
2
2
2t 8
dt = 2t7 dt =
8
x3 dx
0
1
=
0
2.28
− 0 = 64
8
bulunur.
2t7
( x 2 )3
x3
− ( x )′ ⋅ 2
2 2
(x ) + 1
x +1
4
ÖRNEK
x
x6
x3
− 1⋅ 2
x +1
x +1
e2t dt
4
2 1 1
− =
2 2 2
ÖRNEK
2
lim
bulunur.
işleminin sonucu nedir?
x2 – 4
x®2
a
Çözüm
2
Hatırlatma :
f(x) dx = 0
a
x
sinx
d
dx
et dt
e2t dt
işleminin sonucu nedir?
0
lim
x®2
Çözüm
Soruda integralin x değişkenine bağlı türevi sorulmaktadır. Leibnitz Teoremini uygulayabiliriz.
et dt
′ . e0
= (sin x)′ .esin x − (0)
0
0
= cosx.esinx
İntegral
bulunur.
e2t dt
2
x2
=
–4
2
22 – 4
=
0
0
0
ı
belirsizliği L Hospital kuralını uygulayabiliriz.
0
x
e2t dt
sinx
d
dx
2
2
lim
x®2
ı
(x2 – 4)
e2 x − 0 e 4
=
x→2
2x
4
lim
= lim
x→2
( x )′ .e2 x − (2)′ .e2
2x
bulunur.
117
BELİRLİ İNTEGRAL
ADIM GÜÇLENDİRME TESTİ-1
7
1. 7
5. -10
dx +
5
dx
-7
B) – 3
5
fonksiyonunun türevi aşağıdakilerden hangisine
eşittir?
A) 5x + 1 B) 12x
işleminin sonucu nedir?
A) – 5
x +1
dx
x2
f(x) =
C) – 1
D) 1
C) x + 3
D) x E) 0
E) 5
p
2
6. 5
0
2
2. 2
ex dx +
0
5
B) e5
A) ln2
C) 5
D) 0
x7
dx +
D) –ln(1 – ln2)
E) ln(2 + ln2)
3
x7
10
dx
(2x + 3)2
7. dx
1
işleminin sonucu nedir?
işleminin sonucu nedir?
B) 229
C) ln(1 + e)
E) –5
10
0
A) 232
B) –ln2
16
10
3. p
6
işleminin sonucu nedir?
(ex + 1) dx
işleminin sonucu nedir?
A) e25
cot x
dx
1+ In(sin x )
C) 224
D) 212
E) 28
A) 2
9
B) 1
3
C) 4
9
D) 7
9
2
3
E) p
3
4. d
dx
(sinx.cosx + 1)2 dx
3
8. 0
işleminin sonucu nedir?
1
x +1
dx
x 2 + 2x
işleminin sonucu nedir?
A) 3
2
1) C
124
B) 1
2
2) E
C) 1
4
D) 0
3) B
E) -
1
2
4) D
1
1
1
A) In5 B) In3 C) In2 D) 1
2
2
2
5) E
6) D
7) C
E) 0
8) A
İntegral
ALAN HESABI
ADIM
ALAN HESABI
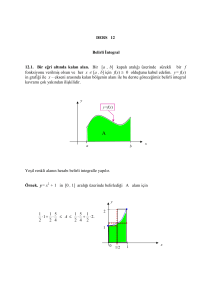
Bir eğrinin altında kalan bölgenin alanı belirli integral yardımıyla hesaplanabilir.
Alanın hesaplanabilmesi için eğrinin altında kalan bölge sonsuz adet küçük dikdörtgenlere bölünür. Elde edilen bu dikdörtgenlerin alanlarının limit
durumda hesaplanması belirli integral yardımıyla
yapılarak oluşan bölgenin alanı bulunur. Bir grafik
üzerinde bu anlattıklarımızı örnekleyelim.
(*) f(x) fonksiyonu x ekseni altında negatif değerlidir. B alan değeri pozitif olduğundan eşitlik için
integralin sonucu (–1) ile çarpılmalıdır
.
c
b
f(x) dx =
a
c
f(x) dx +
a
f(x) dx = A – B olur.
b
Çünkü x ekseni üstündeki bölgede f(x) pozitif
değerli, x ekseni altındaki bölgede f(x) negatif değerlidir.
Şekilde çizilen dikdörtgenin alanı:
dA = f(x) dx
Bu şekilde sonsuz adet dikdörtgenin toplam alanı
ADIM PEKİŞTİRME
b
f(x) dx
ÖRNEK
1
a
integraliyle hesaplanarak eğrinin altında a ile b sınırları arasında kalan bölgenin alanı bulunur.
BİR EĞRİNİN OX EKSENİ İLE ARASINDA
KALAN BÖLGENİN ALANINI BULMA
Yukarıdaki grafikte taralı bölgenin alanı 3 br2 oldu4
ğuna göre
f(x) dx işleminin sonucu nedir?
0
Taralı bölgenin büyüklüğü A ise
Çözüm
b
A =
f(x) dx dir.
a
Şekilde A ve B bölgelerinden oluşan dikdörtgenin alanı
8 br2 dir. A = 3 br2 olduğuna göre, B = 5 br2 olmalıdır. O
halde
b
B =–
f(x) dx ... (*)
a
İntegral
4
B=
f(x) dx = 5 bulunur.
0
137
HACİM HESABI
5. y = x2 + 1 eğrisi, x ≥ 0 ve y = 3 doğrusunun sınırladığı bölgenin y ekseni etrafında döndürülmesi ile
oluşan cismin hacmi kaç br3 tür?
ADIM PEKİŞTİRME TESTİ
1.
A)
Yukarıdaki grafikte gösterilen taralı bölgenin x
ekseni etrafında döndürülmesi ile oluşan cismin
hacmi kaç p br3 tür?
A) e2 –1
B) 2(e2 – 1)
D) e2(e2 – 1)
B)
211
5 4p
3 B)
8p
3 3p
2 D) 2p 5p
3
E)
E) e(e2 – 1)
C)
243
10
D)
Yukarıdaki grafikte gösterilen taralı bölgenin x ekseni etrafında döndürülmesi ile oluşan cismin hacmi kaç br3 tür?
C) 4p D)
A)
221
211
E)
10 10
3. y = 4 − x 2 eğrisinin y ekseni etrafında 180°
döndürülmesi ile oluşan cismin hacmi kaç br3 tür?
A)
C)
C) 2e2(e2 – 1)
parabolü, x = 2 ve x = 3 doğruları ile sınırlı
2. y
=
bölgenin x ekseni etrafında 180° döndürülmesi ile
oluşan cismin hacmi kaç p br3 tür?
243
5 B) p 6.
x2
A)
2p
3 B) 2p C)
11p
6 D) 3p E)
13p
2
7. y = –8x + 8 ve y = –8x + 16 doğruları ile y = 0 doğrusu arasında kalan bölgenin y ekseni etrafında döndürülmesi ile oluşan cismin hacmi kaç br3 tür?
16p
32p
E)
3 3
4.
3p
2 A)
8p
3 B) 4p C)
16p
3 D) 8p 56p
3
E)
8.
Yukarıdaki grafikte gösterilen taralı bölgenin x
ekseni etrafında döndürülmesi ile oluşan cismin
hacmi kaç br3 tür?
A)
8p
5 1) C
158
B)
16p
15 2) E
C)
32p
15 D)
3) D
24p
128p
E)
5 5
4) B
Yukarıdaki grafikte gösterilen taralı bölgenin x ekseni etrafında 90° döndürülmesi ile oluşan cismin
hacmi kaç br3 tür?
A)
5) D
p
120 B)
p
24
6) C
C)
p
15 D)
13p
64p
E)
12
15
7) E
8) B
İntegral
MARATON TESTLERİ
13.
2
2
x
y
+
=4
1
4
9. elipsi tarafından sınırlanan bölgenin alanı kaç br2
dir?
A) p
B) 2p
C) 3p
D) 4p
E) 8p
3t
10.
1
dx
x
lim
t→∞
t
Yukarıdaki grafikte gösterilen taralı bölgenin alanı
kaç br2 dir?
A) p – 3
işleminin sonucu nedir?
A) 0
B) 1
C) ln2
D) ln3
B) p – 2
işleminin sonucu nedir?
y = k. Inx
x
A) sinx – ln |x| + c
B) tanx + c
C) cotx + c
D) ln |sinx| – cosx + c
x
e
E) p + 1
sin2 x + cos x
dx
sin x
y
1
D) p
E) e2
14.
11.
C) p – 1
Yukarıdaki grafikte gösterilen taralı bölgenin OX
ekseni etrafında döndürülmesi ile oluşan cismin
hacmi, sayıca taralı bölgenin alanına eşit olduğuna
göre k kaçtır?
E) ln |sinx| + x + c
p
15.
(x2 + x) cos x dx
0
işleminin sonucu nedir?
2e
A)
3π(e − 2)
D) e
B) π(e − 2)
2e
π(e − 2)
π
C) e(e − 2)
E) πe
3(e − 2)
A) –2p – 2
B) –2p
C) 2p
D) 0
E) 1
16.
12.
y=2ax3
y=3a x
Yukarıdaki grafikte y = 2ax3 , y=3a x eğrileri ve x = a
doğrusu verilmiştir.
Buna göre (S1 – S2) farkının en büyük değerini alması için a nın değeri kaç olmalıdır?
3
A) 2
9) E
182
B)
3
2
10) D
C)
5
3
2
D) 1
11) A
1
E)
2
12) D
Yukarıda gösterilen taralı bölgenin y ekseni etrafında döndürülmesi ile oluşan cismin hacmi kaç
p birim küptür?
A) e4 – e2
13) C
D)
B) e4 + e2
e4
2
14) D
C)
E) e2 + e
15) A
e 4 + e2
2
16) C
İntegral
MARATON TESTLERİ
8.
12.
Yandaki
grafikte
gösterilen taralı bölgenin x ekseni etrafında döndü­rülmesi
ile olu­şan cismin
hacmi kaç p birim
küptür?
Yandaki grafikte
y = ax2 parabolü,
x = a doğrusu ve d
doğrusu verilmiştir.
S1 ve S2 pozitif olmak
üzere üzerin­de yazılı oldukları bölgenin
alanlarını göstermektedir.
S1 – S2 farkının en küçük değerini alması için a kaç
olmalıdır?
A)
1
2
B) 1
C)
3
2
D) 2
E)
5
2
A)
129
5 B)
64
5 C) 24
D) 32
13.
Yandaki
grafikte
gösterilen
taralı
bölgenin x = 3 doğ­
rusu etrafında dön­
dürülmesi ile olu­şan
cismin hacmi kaç
birim küptür?
9.
Yandaki grafikte gösterilen taralı bölgenin alanı
10 br2 olduğuna göre,
A)
2
3p
2 B) 4p C) 5p kezi Oy ekseni üze-
işleminin sonucu nedir?
B) – 10
rinde
C) –8
D) 6
E) 12
sin x
dx
1+ sin x
0
B) 0
çember,
A ve B noktalarına
x2
y=
parabolüne
4
te­ğettir.
B) 10 3 −
A) 10 3
işleminin sonucu nedir?
A) –p
olan
Çemberin yarıçapı 4 br olduğuna göre taralı bölgenin alanı kaç birim karedir?
p
10.
16p
19p
E)
3 6
Yandaki grafikte mer-
0
A) –14
D)
14.
ı
x .f (x) dx
E) 36
D) 9 3p C) 1
D) p – 2
E) p + 1
7π
16π
C) 12 3 −
3
3
E) 16 3 15.
Yandaki grafikte gösterilen taralı bölgenin alanı
p
4
11.
A(x), OABC dikdörtgeni-
(tan3x + 1) (cot2x + 1) dx
nin alanı B(x) olduğuna
A( x )
işleminin
göre, xlim
→∞ B( x )
p
6
işleminin sonucu nedir?
A)
3
1
- 2 B)
2
2
8) C
192
9) D
C)
3-
1
2
D)
2
3
10) D
sonucu kaçtır?
E)
3 +2
A)
11) C
1
4
12) A
B)
1
3
13) E
C)
2
5
D)
14) C
2
3
E) 1
15) B
İntegral