ç alı ş manotları

Sinyaller & Sistemler - Sinyaller
VEKTÖRLER
I
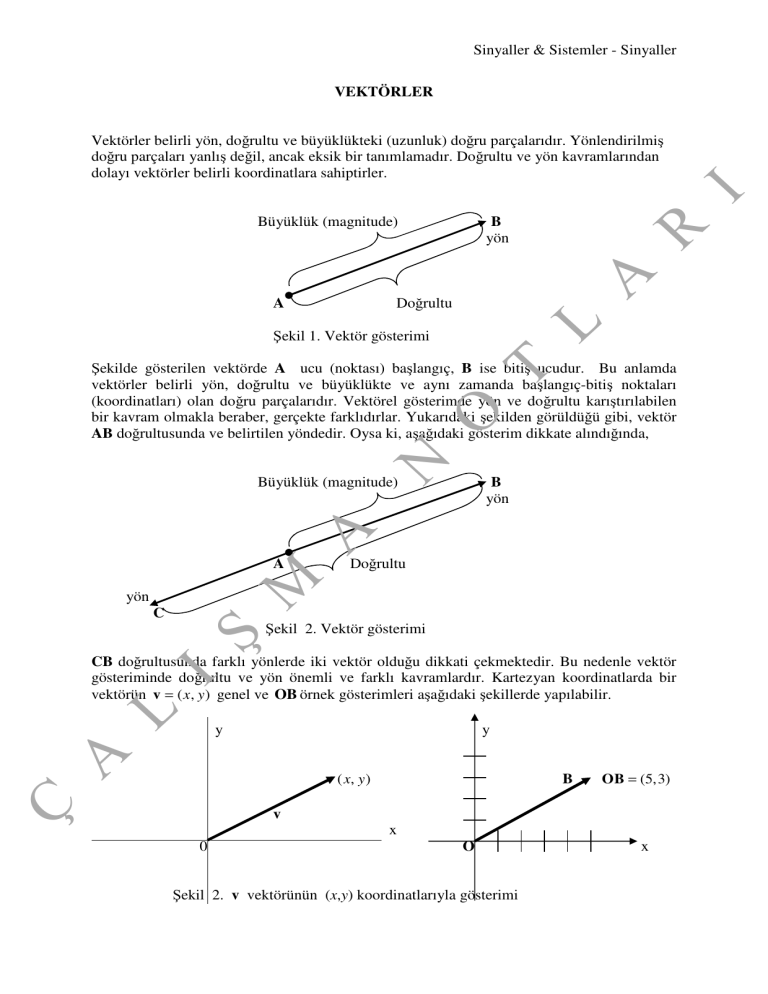
Vektörler belirli yön, doğrultu ve büyüklükteki (uzunluk) doğru parçalarıdır. Yönlendirilmiş
doğru parçaları yanlış değil, ancak eksik bir tanımlamadır. Doğrultu ve yön kavramlarından
dolayı vektörler belirli koordinatlara sahiptirler.
A
A
R
B
yön
Büyüklük (magnitude)
L
Doğrultu
Şekil 1. Vektör gösterimi
N
O
T
Şekilde gösterilen vektörde A ucu (noktası) başlangıç, B ise bitiş ucudur. Bu anlamda
vektörler belirli yön, doğrultu ve büyüklükte ve aynı zamanda başlangıç-bitiş noktaları
(koordinatları) olan doğru parçalarıdır. Vektörel gösterimde yön ve doğrultu karıştırılabilen
bir kavram olmakla beraber, gerçekte farklıdırlar. Yukarıdaki şekilden görüldüğü gibi, vektör
AB doğrultusunda ve belirtilen yöndedir. Oysa ki, aşağıdaki gösterim dikkate alındığında,
B
yön
Doğrultu
M
A
A
Büyüklük (magnitude)
yön
Ş
C
Şekil 2. Vektör gösterimi
L
I
CB doğrultusunda farklı yönlerde iki vektör olduğu dikkati çekmektedir. Bu nedenle vektör
gösteriminde doğrultu ve yön önemli ve farklı kavramlardır. Kartezyan koordinatlarda bir
vektörün v = ( x, y ) genel ve OB örnek gösterimleri aşağıdaki şekillerde yapılabilir.
y
A
y
B
Ç
( x, y )
OB = (5,3)
v
x
0
O
Şekil 2. v vektörünün (x,y) koordinatlarıyla gösterimi
x
Vektörlerin Matrisyel Gösterimi
Örneğin ( x1 , x2 ) koordinatlarından oluşan iki boyutlu bir nokta x vektörü ile klasik
I
 x1 
x = ( x1 , x2 ) biçiminde veya x =  
 x2 
R
gibi sütun matrisi formunda gösterilebilir, diğer bir deyişle
A
 x1 
x = ( x1 , x 2 ) =  
 x2 
L
Vektörlerin skalerle çarpımı
Eğer vektörümüz v = (v1 , v 2 , v3 ) ise, bir “ c “ sabiti (skaler) ile çarpımı,
−2v
N
O
T
c v = c (v1 , v 2 , v3 ) = (cv1 , cv 2 , cv3 )
3v
v
A
½v
M
Şekil 3. Vektörlerin skalerlerle çarpımı
x2
I
Ş
Norm : Vektör uzunluğu
Ç
A
L
( x1 , x2 )
0
x1
2
Şekil 4. Gerçek vektörlerin R deki uzunluğu
Burada x1 ve x 2 R 2 de yani iki boyutlu gerçek sayılar için tanımlıdırlar. Şekilden görüldüğü
gibi x1 ve x 2 vektörlerinden oluşan R 2 deki x vektörünün uzunluğu norm olarak anılır ve
x ile gösterilir. Buna göre x = ( x1 , x 2 ) ∈ R 2 olarak verilen x in uzunluğu :
2
Sinyaller & Sistemler - Sinyaller
x = x12 + x 22 = x
I
Norm görüldüğü kadarıyla bir vektörün büyüklüğünü gösteren kavramdır. Bu anlamda bir
vektörün büyüklüğünü gösteren bu kavramın, işaret analizde işaretin enerjine karşılık
gelmektedir.
Skaler çarpım olarak anılan bu işlemde eğer iki gerçek vektör,
x = ( x1 , x 2 , , x n )
ve
A
y = ( y1 , y 2 , , y n ) iseler, x, y ∈ R n olmak üzere bunların içsel çarpımları x ⋅ y ,
L
x ⋅ y =< x, y >= x1 y1 + x 2 y 2 + + x n y n
Buna göre , x.x = x 2
2
T
x.x = x 2 = x
R
Gerçek vektörlerin içsel çarpımı (skaler çarpım)
O
Kompleks Değerli Hilbert Space’in (Inner product Space) Özellikleri
N
Şimdi vektörleri daha genel olacak şekilde kompleks değerlikli Hilbert vektör uzayında
kompleks vektörlerin içsel çarpımını yani skaler çarpımını ele alacağız. x ve y vektörleri
kompleks olduklarından,
x = ( x1 , x2 , , xn ) ve y = ( y1 , y2 , , yn )
∑x
k
A
n
x, y ∈ C n olmak üzere,
⋅ y k = x1 y1 + x 2 y 2 + + x n y n
k =1
M
Bu nedenle
Ş
x⋅y ≠ y ⋅x
L
I
olduğundan, gerçek sayılardaki R n , x ⋅ y = y ⋅ x ifadesi ile karıştırılmamalıdır.
İki Vektör Arasındaki Açı
Ç
A
x
θ
y
Şekil 5. x ve y vektörleri
x.y = < x, y > = x y cosθ
vektör uzunluklarını norm olarak da ifade edebiliriz.
x.y = < x, y > = x y cosθ
I
x.y
x y
x.y
x y
A
θ = cos −1
R
cos θ =
2
T
x⋅x = x
L
Görüldüğü gibi, iki vektörün içsel çarpımları bir sayı olup vektör değildir. Buradan eğer iki
vektör x ve x ise, içsel çarpımları,
O
biçiminde vektörün uzunluğunu gösteren norm olarak hesaplanabilir. İçsel çarpımın diğer bir
faydası da seçilen vektörlerin ortogonal olmalarıyla ilgilidir. İki vektör birbirlerine dik iseler
(aralarındaki açının cos’u 90 0 )
N
x ⋅ y = x y cos 90
x⋅ y = y⋅x = 0
A
Bu yaklaşım vektörlerin birbirlerine benzerliklerini inceleme açısından önemlidir.
cosθ =
< x, y >
x y
M
Ortogonal Vektörler
π
2
I
Ş
cosθ = 0 veya θ = 90 0 =
L
Bu durumdaki x ve y vektörlerinin ortogonal olduğu kabul edilir. Verilen bağıntıdan
yararlanarak alternatif olarak ortogonallik koşulunun θ = 90 0 yanısıra
A
< x, y >= 0
Ç
Sonuç 1 : Vektörler ortogonal iseler aralarındaki açı θ = 90 0 ve içsel çarpımları sıfır (
< x, y >= x.y = 0 ) olmalıdır.
Ortonormal Vektörler
x ve y vektörleri ortogonal, birbirlerine dik, aralarındaki açı θ = 90 0 , ve de içsel çarpımları
x y = 0 ve uzunlukları “1” ise x = 1 ve y = 1 vektörler ortonormal olarak anılırlar.
.
4
Sinyaller & Sistemler - Sinyaller
Örnek
x = (9,−2)
, y = ( 4,18)
, ise θ = ?
x = 9 2 + (−2) 2 = 85
I
y = 4 2 + 18 2 = 340
R
x.y = < x, y > = x y cosθ
x.y
x.y (9.4 + (-2)18)
0
=
=
=0
x y
x y
85 340
85.340
cos θ = 0
π
θ = = 90 0
2
L
A
cosθ =
T
Bu durumda x ve y vektörleri ortogonaldir.
O
Orthogonal projeksiyon (grafik yaklaşım)
→
N
u
→
A
v2
M
→
→
→
→
v1
a
→
Pr oj → u = v1
a
→
Şekil 6. u vektörünün a üzerine projeksiyonu
→
→
→
→
u ≅ca
→
I
→
Ş
u = v1 + v 2
→
L
v1 = c a
→
→
→
Ç
A
u = c a + v2
→
her iki tarafı a ile çarparsak,
→ →
→
→
→
→ →
→ →
u . a = (c a + v 2 ). a = c a . a + v 2 . a
0
→ →
= c a.a
→ →
=
u .a
→ →
=
a.a
u .a
u . a < u, a >
=
a . a < a, a >
2
a
I
c=
→
R
Bu durumda aranan projeksiyon,
→
Pr oj→ u = v1 = Pr ojau = v1 = c a
a
u.a
a =
2
a
< u, a >
< u, a >
a =
a
2
< a, a >
a
A
=
,
a = (7,2) ise, Pr ojau = ?
T
u = ( −3,1)
L
Örnek
2
= ( 7 2 + 2 2 ) 2 = 53
v1 = Pr ojau =
u .a
a
2
a =
−19
 133 38 
(7, 2) =  −
,− 
53
 53 53 
N
a
O
u . a = (−3.7 + 1.2) = −19
1 3 2 

 matrisinin ortogonal özelliğini araştırın.
13 2 − 3
M
A=
A
Örnek
Çözüm
Ş
Öncelikle verilen matrisin A1 ve A 2 vektörlerini yazalım.
I
1  3
1 2
 2 , A 2 =
 
13  
13 − 3
L
A1 =
Ç
A
Şimdi bu vektörlerin ortogonalliklerini test edelim.
A1A 2 =
1
13
3 
1 2 1
2  ×
  = (3.2 + 2.(−3)) = 0
13 − 3 13
 
Vektörlerin ortogonal oldukları görülmektedir. Ancak bunun A matrisinin de ortogonal
olacağı anlamına gelemeyeceğini bir önceki örnekten biliyoruz. Bunun için verilen vektörlerin
bu kez ortonormalliğini test edelim. Eğer vektörler ortogonal ve uzunlukları “ 1 “ ise,
vektörler ortonormal olacaklardır. Bunun için sırasıyla iki vektörün uzunluklarını
hesaplayalım.
6
Sinyaller & Sistemler - Sinyaller
3 2
2 2
9
4
13
) +(
) =
+
=
=1
13 13
13
13
13
A2 = (
2 2
−3 2
4
9
13
) +(
) =
+
=
=1
13 13
13
13
13
Buradan her iki vektörün uzunluklarının da “ 1 “ olduğunu ,
A1 = A 2 = 1 olduğu
I
A1 = (
L
ÖZDEĞER – ÖZVEKTÖR (eigenvalue – eigenvector)
A
R
görülmektedir. Vektörler hem ortogonal ( A1 A 2 = 0 ), hem de birim uzunlukta olduklarından,
sonuçta vektörler ortonormaldirler.
T
Ax = λ x
O
Örnek
N
− 7 
− 5 7 
x =   Vektörünün A x = λ x işlemi gereğince A = 
 matrisinin öz vektörü
 4
 4 − 2
olabileceğini gösterin.
Çözüm
M
A
− 5 7  − 7  − 5.(−7) + 7.4  35 + 28   63 
− 7 
Ax = 
=
=
=
= −9  






 4 − 2  4  4.(−7) + (−2).4 − 28 − 8 − 36
4 
Ax=λx
I
Ş
olduğundan, x vektörü A matrisinin öz vektörüdür.
Ax = λ x
Ç
A
L
λIx−Ax=0
(λ I − A ) x = 0
det(λ I − A) = 0 = λ I − A
λI−A =0
Kare matrisin öz değerleri
λI−A =
− a1n
λ − a 22 − a2n
− a12
− a 21
− a n1
− an2
λ − a nn
I
λ − a11
R
= λ n + a1λ n −1 + + a n −1λ + a n = 0
Örnek
L
A
 −8 4 
A=
 Matrisinin öz değer ve öz vektörlerini hesaplayın.
 5 −9 
Çözüm
T
(λ I − A ) x = 0
O
İlk bölümde ( A − λ I)x = 0 ile elde edilen öz değerler ve öz vektörler şimdi (λ I − A)x = 0
kullanılarak teyit edilmeye çalışılacaktır.
λ 0 

0 λ 
λI=
N
1 0
 −8 4 
A=
, I=
 ve

 5 −9 
0 1 
A
(λ I − A ) x = 0
 λ 0   −8 4  λ + 8 −4 
−
=

 0 λ   5 −9   −5 λ + 9 
λ +8
−4
−5
λ +9
= (λ + 8)(λ + 9) − [ −4.(−5)] = λ 2 + 17λ + 72 − [ 20] = λ 2 + 17λ + 72 − 20
Ş
λ I−A =
M
λ I−A =
I
λ I − A = 0 için
λ1 = −4 , λ2 = −13
L
λ 2 + 17λ + 52 = 0 →
Ç
A
Öz değerler ayrı ve farklı elde edilmiştir. Bunların ardından, λ1 = −4 öz değerine karşılık
gelen öz vektörü hesaplayalım. Bunun için öz değeri (λ I − A)x = 0 matrisinde yerine
koyalım.
−4   x1   0 
λ + 8
(λ1 I − A )x =  1
  = 
 −5 λ1 + 9   x2   0 
−4   x1   0   4 −4   x1  0 
 −4 + 8
(−13I − A ) x = 0 → 
=
→
=
−4 + 9   x2   0   −5 5   x2  0 
 −5
8
Sinyaller & Sistemler - Sinyaller
4 x1 − 4 x2 = 0
−5 x1 + 5 x2 = 0
→ x1 = x2 → x2 = a → x1 = a
I
 x  a 
1 1
x1 =  1  =   = a   =  
1 1
 x2   a 
R
Şimdi λ2 = −13 öz değerine karşılık gelen öz vektörü hesaplayalım. Bunun için öz değeri
(λ2 I − A ) x 2 = 0 matrisinde yerine koyalım.
L
A
−4   x1  0 
λ + 8
(λ2 I − A ) x = 0 →  2
=
λ2 + 9   x2  0 
 −5
−5 x1 − 4 x2 = 0
→ x1 = −
4 x2
→ x2 = 5a → x2 = −4a
5
O
−5 x1 − 4 x2 = 0
T
−4   x1   0   −5 −4   x1  0 
 −13 + 8
(−13I − A ) x = 0 → 
=
→
=
−13 + 9   x2   0   −5 −4   x2  0 
 −5
N
 x   −4 a 
 −4   −4 
x2 =  1  = 
=a  = 

5 5
 x2   5a 
A
Buna göre verilen sistemin λ1 = −4 ve λ2 = −13 reel ve farklı öz değerlerine karşılık gelen
öz vektörleri,
M
1
 −4 
x1 =   ve x 2 =  
1
5
Ş
Örnek
I
 −4 5 
A=
 Matrisinin öz değer ve öz vektörlerini hesaplayın.
 −5 4 
L
Çözüm
Ç
A
1 0
 −4 5 
A=
, I=
 ve

 −5 4 
0 1 
λ 0 

0 λ 
λI=
(λ I − A ) x = 0
 λ 0   −4 5   λ + 4 −5 
−
=
λ − 4 
 0 λ   −5 4   5
λ I−A = 
λ I−A =
λ+4
−5
5
λ −4
= (λ + 4)(λ − 4) − [ −5.5] = λ 2 − 16 − [ −25] = λ 2 − 16 + 25
λ I − A = 0 için
λ1 = j 3 , λ2 = − j 3
I
λ2 + 9 = 0 →
R
Öz değerler tam kompleks olarak elde edilmiştir. İlk olarak λ1 = j 3 öz değerine karşılık gelen
öz vektörü hesaplayalım. Bunun için öz değeri (λ I − A)x = 0 matrisinde yerine koyalım.
L
5 x2
→ x2 = (4 + j 3)a → x1 = 5a
4 + j3
O
x1 =
(4 + j 3) x1 − 5 x2 = 0
−5   x1  0 
= →



j 3 − 4   x2  0  5 x1 + (−4 + j 3) x2 = 0
T
 j3 + 4
( j 3I − A )x = 0 → 
 5
A
−5   x1   0 
λ + 4
(λ1 I − A )x = 0 →  1
  x  = 0
5
−
4
λ

1
  2  
N
 x   5a 
 5   5 
x1 =  1  = 
= a

=

 4 + j 3   4 + j 3
 x2  (4 + j 3)a 
A
Şimdi λ2 = − j 3 öz değerine karşılık gelen öz vektörü hesaplayalım. Sonuçta öz değerlerin
kompleks ve eşlenik olması durumunda öz vektörlerde eşlenik olacağından,
M
 x   5a 
 5   5 
x2 =  1  = 
=a

=

 4 − j 3  4 − j 3
 x2  (4 − j 3)a 
Ş
Örnek
I
2 0 
A=
 Matrisinin öz değerlerini ve öz vektörlerini hesaplayın.
0 2 
L
Çözüm
Ç
A
A matrisi 2 x 2 boyutlu olduğundan, üç öz değer ve bunlara karşılık gelen iki lineer bağımsız
öz vektörün elde edilmesini bekliyoruz.
 2 0  λ
A− λI = 
−
0 2   0
2−λ
0
A− λI =
0
2−λ
0  2 − λ
=
λ   0
0 
2 − λ 
= (2 − λ ).(2 − λ ) = (2 − λ ) 2
A − λ I = 0 → (λ − 2) 2 = 0 , λ1 = λ2 = 2
10
Sinyaller & Sistemler - Sinyaller
Sistemin karakteristik denkleminden λ1 = λ2 = 2 olarak katlı öz değerlerin söz konusu
olduğunu görmekteyiz Bu doğrultuda söz konusu katlı öz değere karşılık gelen öz vektörleri
elde etmeye çalışalım. λ1 = λ2 = 2 öz değeri için,
( A − λ I)x = 0
A
R
I
0   x1  2 − 2
0   x1 
2 − λ
0 0  x1 
A− λI = 
=
→






 
2 − λ   x2   0
2 − 2  x2 
 0
 0 0  x 2 
0 0   x1  0  0.x1 + 0.x2 = 0
0 0   x  = 0  → 0.x + 0.x = 0

  2  
1
2
T
L
Son yazılan 2x2 lineer bağımsız denklem sisteminde katsayılar sıfır olduğundan x1 ve x2 ne
alınırsa alınsın sonuç (sıfır) değişmeyecektir. Bu durumda x1 ve x2 keyfi seçilebilir. Birinci
1 
öz vektör için x1 = 1 ve x2 = 0 , x1 =   , ikinci öz vektör için ise x1 = 0 ve x2 = 1 olarak
0 
0 
2 0 
x 2 =   alınabilir. Buna göre A = 
 tipindeki diyagonal matrislerin öz vektörleri
1 
0 2 
N
O
1 
0 
x1 =   ve x 2 =   tipindeki standart vektörlerdir. Diğer bir deyişle x1 ve x 2 , A
0 
1 
matrisinin öz vektörleridir.
A
Öz Değerlerin Lineer Sistem Davranışının Belirlenmesine Etkisi
M
Lineer sistemlerde y (t ) sistem çıkışı genellikle karekteristik mod olarak anılan eλi t tipli
exponensiyellerin ci katsayılarından içeren lineer kombinasyonlarından oluşmaktadır.
y (t ) = c1eλ1 t + c2 eλ2 t + c3eλ3 t + + cn eλn t
I
Ş
Bu gösterimdeki λi öz değerlerin, genel olarak λi = ai ∓ jωi yapısında olmasına göre öz
değerler farklı tiplere ayrılırlar.
Ç
A
L
1 Reel öz değerler : λi = ai ( ωi = 0 için)
2.Kompleks öz değerler ( λi = ai + jωi )
3. Katlı öz değerler : λi = λi +1 ( ωi = 0 için)
Bu noktadan itibaren göz önüne alınacak örneklerde, öz değerlerin sistem etkisi de ayrıca
değerlendirilecektir.
Örnek
7 − 1
A=
 Matrisinin öz değerlerini ve öz vektörlerini hesaplayın.
6 2 
I
Çözüm
7 − 1
1 0
A=
, I=

 ve
6 2 
0 1 
λ 0 

0 λ 
R
λI=
A
(λ I − A ) x = 0
1 
λ 0  7 − 1 λ − 7
−
=



 0 λ  6 2   − 6 λ − 2 
λ −7
1
−6
λ −2
T
λI−A =0=
L
λI−A=
= (λ − 7)(λ − 2) − [− 6.1] = λ2 − 9λ + 14 + 6 = λ2 − 9λ + 20 = 0
O
λ2 − 9λ + 20 = 0
N
λ1 = 4 , λ2 = 5
Not : Lineer zamandan bağımsız (Linear Time Invariant, LTI system) sistem için iki öz
değerin pozitif oluşu, sistemi kararsızlığa götürmektedir.
M
A
Bunların ardından, λ1 = 4 öz değerine karşılık gelen öz vektörü hesaplayalım. Bunun için öz
değeri (λ I − A ) x = 0 matrisinde yerine koyalım.
Ç
A
L
I
Ş
1   x1  0
λ − 7
(λ I − A ) x = 
 = 
 − 6 λ − 2   x 2  0 
1   x1  0
4 − 7
 − 3 1  x1  0
(λ I − A ) x = 
= →



 = 
 − 6 4 − 2   x 2  0 
 − 6 2   x 2  0 
− 3 x1 + x2 = 0
x
→ x1 = 2 → x2 = 3a olsun
− 6 x1 + 2 x2 = 0
3
x1 = a
 x1  a 
1 
1 
x1 =   =   = a   → x1 =  
3
3
 x2  3a 
Şimdi λ2 = 5 öz değerine karşılık gelen ikinci öz vektörü hesaplayalım. Bunun için öz değeri
(λ I − A)x 2 = 0 matrisinde yerine koyalım.
1   x1  0
λ − 7
(λ I − A ) x 2 = 
 = 
 − 6 λ − 2   x 2   0
12
Sinyaller & Sistemler - Sinyaller
 x  a 
1 
x2 =  1  =   = a  
 2
 x2   2a 
I
1   x1  0
5 − 7
− 2 1  x1  0
(λ I − A ) x 2 = 
=
→
   
− 6 3  x  = 0
 − 6 5 − 2   x 2  0 

  2  
− 2 x1 + x2 = 0
x
→ x1 = 2 → x2 = 2a
− 6 x1 + 3 x2 = 0
2
x1 = a
R
1 
→ x2 =  
2
A
Reel öz değerler ve sistem davranışı :
L
Lineer sistemin öz değerleri reel ise sistemin davranışı aşağıdaki çıkış denkleminden
belirlenir.
T
y (t ) = c1eλ1 t + c2 eλ2 t + c3eλ3 t + + cn eλn t
O
Bu genel ifadenin ışığında örnekteki lineer sisteme ait öz değerleri ( λ1 = 4 , λ2 = 5 ), reel ve
pozitif olduğundan, kararsız davranacaktır. Bu durumda sistem çıkışının sonsuz uzun bir
sürede sükûnete yani başlangıç koşullarına varamayacağı, sonsuza/belirsizliğe gideceği
düşünülür ( y (t ) → ∞ ). Bu durumdaki y(t ) sistem çıkışı aşağıdaki değişimleri gösterir.
N
t →∞
y (t ) = y1 (t ) + y2 (t ) = c1e4 t + c2 e5 t
A
Not : c1 ve c2 sistem katsayıları başlangıç koşullarıyla hesaplanır.
M
SONUÇ : Öz değerler reel ve pozitif ise sistem kararsız davranır ( λi > 0 )
y2 (t ) = c2 e5 t
I
Ş
y1 (t ) = c1e 4 t
λ1 = 4 > 0
λ2 = 5 > 0
L
c1
Ç
A
0
c2
t
t
0
Şekil 17 Poziitif öz değerlerin ( λ1 = 4 , λ2 = 5 ) sistem kararlılığı üzerindeki etkisi
Örnek
5
6
A=
 Kare matrisinin öz değerlerini hesaplayın.
− 8 − 6
I
Çözüm
R
Bunun için (λi I − A) x i = 0 gereği, λ I − A karakteristik polinomundan, λ I − A = 0
karakteristik denklemini oluşturalım. Köşegen matris I,
A
λ −6
−5
8
λ +6
L
λI−A =
5  λ − 6 − 5 
λ 0 
λ 0   6
Z=λI=
−
→ λI−A=


=
λ + 6
0 λ 
 0 λ  − 8 − 6  8
= (λ − 6).(λ + 6) − [− 5.8] = λ2 − 36 + 40 = λ2 + 4
T
1 0 
I=
 ve
0 1 
λ I − A = 0 için öz değerler,
ve λ2 = −2 j
N
λ1 = 2 j
O
λ2 + 4 = 0 → λ2 = −4 = 4 j 2
(λ1 I − A ) x1 = 0 için
A
Öz değerler kompleks (imajiner) olarak elde edilmiştir. İlk olarak λ1 = 2 j kompleks öz
değerine karşılık gelen kompleks öz vektörü hesaplamaya çalışalım.
Ş
M
−5   x1  0 
λ − 6 −5   x1   2 j − 6
(λ1 I − A ) x1 = 
=
=



2 j + 6   x2  0 
λ + 6   x2   8
 8
−5   x1  0 
( j − 3) x1 − 5 x2 / 2 = 0
2 j − 6
= →


 8

4 x1 + ( j + 3) x2 = 0
2 j + 6   x2  0 

I
5 x2
5(− j − 3) x2
−5( j + 3) x2 −5( j + 3) x2 −5( j + 3) x2 (3 + j ) x2
→ x1 =
=
=
=
=
2( j − 3)
2( j − 3)( j + 3) 2( j 2 − 32 )
2(−1 − 9)
2(−10)
4
L
x1 =
Ç
A
 x1 
(3 + j ) x2 / 4 
 (3 + j ) / 4  (3 + j ) / 4 
x1 =   = 
=
x
2


=

x2
1
1

 

 x2 


Şimdi λ2 = −2 j kompleks öz vektörüne karşılık gelen ikinci kompleks öz vektörü
hesaplayalım.
(3 + j ) / 4 
 −(3 + j ) / 4 
x1 = 
ve x 2 = 


1
1




Kompleks öz değerlere karşılık gelen öz vektörlerde kompleks ve eşleniktir.
14
Sinyaller & Sistemler - Sinyaller
Tam kompleks öz değerler ve sistem davranışı :
Sistemin öz değerleri kompleks ise sistemin davranışı aşağıdaki çıkış denkleminden belirlenir.
I
y (t ) = c1e j λ1 t + c2e j λ2 t + c3e j λ3 t + + cn e j λn t
y (t ) = e ± j ω t = cos ωt ± j sin ωt
;
Buna göre ele aldığımız örnekte elde edilen
Euler eşitlikleri
λ1,2 = ±2 j kompleks öz değerlerini dikkate
e j 2 t − e− j 2 t
sin ωt = sin 2t =
2j
N
;
O
aldığımızda aslında ω = 2 rad/sn olduğundan,
e j 2 t + e− j 2 t
cos ωt = cos 2t =
2
A
e j α + e− j α
2
jα
e − e− j α
sin α =
2j
cos α =
L
e− j α = cos α − j sin α
Euler denklemi
T
e j α = cos α + j sin α
R
y (t ) = eλ t = e± j ω t
A
Denklemde yer alan cos ωt ,sin ωt gibi sinusoid fonksiyonlardan dolayı sistemde
dalgalanma/osilasyon oluşması, kararlılığı engellemektedir. Bu durumda sistemde kararlılık
ve kararsızlık arasında bir karekter olarak marjinal kararlı davranacaktır. Sistem için riskli
olan bu durumda sistemin dalgalı yani osilasyonlu/titreşimli olması kararlılığı tehdit
etmektedir. Sistem ne tam anlamıyla sükûnete ( y (t ) → 0 ) ne de sonsuza ( y (t ) → 0 )
t →∞
t →∞
M
gitmemekle beraber yine de oluşturmaktadır.
Ş
Örnek
L
I
 4 10 
A=
 Matrisinin öz değerlerini hesaplayın.
 −2 8 
Çözüm
Ç
A
Bunun için ( A − λi I ) xi = 0 gereği, A − λ I karekteristik polinomundan, A − λ I = 0
karakteristik denklemini oluşturalım. Köşegen matris I,
1 0
λ 0 
 4 10  λ 0   4 − λ 10 
I=
ve Z = λ I = 
→ A−λ I = 


−
=

 −2 8   0 λ   −2 8 − λ 
0 1 
0 λ
4 − λ 10
A−λ I =
= (4 − λ ).(8 − λ ) − [10.(−2) ] = λ 2 − 12λ + 32 − [ −20] = λ 2 − 12λ + 32 + 20
−2 8 − λ
A − λ I = 0 için,
ve λ2 = 6 − j 4
Öz değerler reel kısmından dolayı yarı kompleks olarak elde edilmiştir. İlk olarak λ1 = 6 + j 4
için öz vektörü hesaplamaya çalışalım.
R
( A − λ1 I ) x1 = 0 için
I
λ 2 − 12λ + 52 = 0 → λ1,2 = 6 ± j 4 → λ1 = 6 + j 4
L
A
10
 4 − λ 10   x1   4 − (6 + j 4)
  x1  0 
=
( A − (6 + j 4) I ) x1 = 



  x  = 0 
−
−
−
−
+
x
j
2
8
2
8
(6
4)
λ

  2 
  2  
10   x1  0   −2 − j 4
10   x1  0 
4 − 6 − j 4
=
= →
=



8 − 6 − j 4   x2  0   −2
2 − j 4   x2  0 
 −2
T
−(2 + j 4) x1 + 10 x2 = 0
−2 x1 + (2 − j 4) x2 = 0
O
(1 + j 2) x1
(1 + j 2)(1 − j 2)a (12 − (− j 2)2 )a (1 + 4)a 5a
x1 → x1 = (1 − j 2)a için x2 =
=
=
=
=a
5
5
5
5
5
x 
 (1 − j 2) a 
1 − j 2  1 − j 2 
x1 =  1  = 
= a

=

a


 1   1 
 x2 
N
x2 =
A
Öz değerler reel kısmından dolayı yarı kompleks olarak elde edilmiştir. İlk olarak λ2 = 6 − j 4
için öz vektörü hesaplamaya çalışalım.
M
x 
 (1 + j 2) a 
1 + j 2  1 + j 2 
x2 =  1  = 
= a

=

a


 1   1 
 x2 
1 − j 2 
1 + j 2 
, λ2 = 6 − j 4 için x 2 = 


 1 
 1 
I
Ş
λ1 = 6 + j 4 için x1 = 
L
y (t ) = y1 (t ) + y2 (t ) = c1e(6+ j 4) t + c2 e (6 − j 4) t = c1e 6 t e j 4 t + c2 e6 t e − j 4 t
Ç
A
= c1 (cos 4t + j sin 4t )e6 t + c2 (cos 4t − j sin 4t )e6 t
c1 ve c2 sistem katsayıları başlangıç koşullarıyla hesaplanır.
Öz değerler yarı kompleks ve reel kısmı pozitif ise sistem kararsız davranır
( λ = a ± jω , a > 0 )
16
Sinyaller & Sistemler - Sinyaller
y(t ) = e λ t = e (σ + jω) t
e6 t
0
R
I
6 > 0, eλ t → ∞
A
t
ej 4t
T
L
λ = 6 ± j4
O
Şekil 24 REZONANS : Sabit frekanslı, genliği zamanla monoton artan sönümsüz/kararsız
sinusoidal olan kararsız sistem : y (t ) = e λ t = e(σ ± jω) t = e(6 ± j 4) t
N
Örnek
A
 3 −18
A=
 Matrisinin öz değerlerini ve öz vektörlerini hesaplayın.
 2 −9 
Çözüm
M
A matrisi 2 x 2 boyutlu olduğundan, üç öz değer ve bunlara karşılık gelen iki lineer bağımsız
öz vektörün elde edilmesini bekliyoruz.
I
Ş
−18 
 3 −18 λ 0  3 − λ
A−λ I = 
−
=


−9 − λ 
 2 −9   0 λ   2
3− λ
−18
A−λ I =
= (3 − λ ).(−9 − 3) − [ −18.2] = λ 2 + 6λ − 27 − [ −36] = λ 2 + 6λ − 27 + 36 = λ 2 + 6λ + 9
2
−9 − λ
L
A− λI =0
Ç
A
λ 2 + 6λ + 9 = (λ + 3)2 = 0
λ1 = λ2 = −3
Sistemin karakteristik denkleminden λ1 = λ2 = −3 olarak katlı öz değerlerin söz konusu
olduğunu görmekteyiz Bu durumda bu öz değere karşılık gelen öz vektörleri elde etmeye
çalışalım. λ1 = λ2 = −3 öz değeri için,
( A − λ I)x = 0
3 − λ
A−λ I = 
 2
−18   x1  3 − (−3)
−18   x1  3 + 3 −18   x1   6 −18  x1 
=
→
→
−9 − λ   x2   2
−9 − (−3)   x2   2
−9 + 3  x2   2 −6   x2 
6 x1 − 18 x2 = 0
→ x1 = 3 x2
I
2 x1 − 6 x2 = 0
3  3 
1 = 1
   
A
3a 
x1 =   = a
a
R
x2 → a , x1 = 3a
L
A matrisinin iki (katlı) öz değeri olmasına karşın lineer bağımsız tek öz vektörünün
x1 = (3,1)T olduğunu görmekteyiz. Bu öz vektörün A matrise ait olduğunu
T
( A − λ1I )x1 = 0 veya Ax1 = λ1x1
3 3.3 + (−18).1 9 − 18  −9 
1  =  2.3 + (−9).1  =  6 − 9  =  −3 = −3.
  
 
  
N
 3 −18
 2 −9 


O
bağıntılarından gösterebiliriz.
3 
1 = λ1x1
 
A
A matrisinin ikinci bir öz vektörü olmadığından bunu, genelleştirilmiş öz vektör yaklaşımıyla
hesaplamamız gerekiyor.
( A − λ I )x k +1 = x k
M
bağıntısından elde edebiliriz.
Ş
( A − λ I )x k +1 = x k → ( A − λ2 I )x 2 = x1
I
( A − λ2 I)x 2 = x1
Ç
A
L
−18   x1  3 3 − (−3)
−18   x1  3 3 + 3 −18   x1  3
3 − λ
= →
=
→
=


 2

−9 − λ   x2  1  2
−9 − (−3)   x2  1  2
−9 + 3  x2  1

6 x1 − 18 x2 = 3
 6 −18  x1  3
1 + 6 x2
1
, x2 = 0 (keyfi) → x1 =
 2 −6   x  = 1 → 2 x − 6 x = 1 → x1 = 2
2

  2  
1
2
 x1  1/ 2
x2 =   = 

 x2   0 
Verilen örnekte katlı öz değerler katlı ve negatif ( λ1 = λ2 = −3 < 0 ) olduğundan, genel çıkış
ifadesi aşağıdaki gibi olacaktır.
18
Sinyaller & Sistemler - Sinyaller
  3
 3
1/ 2  −3 t 
y (t ) = c1x1eλ t + c2 (t x1 +x 2 )eλ t = c1   e−3 t + c2    t e−3 t + 
e 
1 
 0 
 1 

I
Çıkış ifadesindeki t e −3 t teriminin zaman sonsuz geniş iken ( t → ∞ ) sıfıra gideceğini
biliyoruz. Çünkü sistemdeki öz değer negatif ( λ1 = λ2 = −3 < 0 ) durumdadır. Bu durumda
t e −3 t → 0 olacağı söylenebilir.
t →∞
A
t →∞
1
1
= ∞ ×0 → 0
∞ = (∞ ) ×
∞
e
R
t e −3 t = ( ∞ ) e −3 ∞ = ( ∞ ) e −∞ = ( ∞ )
L
Negatif öz değere sahip e λ t exponensiyeli, zamanın sonsuz olmasından önce ( t → ∞ ) daha
kısa sürede kendisini sıfırlayacağından sistemin toplam çıkışıda sonsuz değil, sıfır olur
( t e −3 t → 0 ). Bu genel ifadenin ışığında sistem katlı öz değerlerinin negatif veya pozitif
t →∞
T
olması halinde sistem davranışı olarak y(t ) çıkışı aşağıdaki değişimleri gösterir.
O
y (t ) = c1x1e −3 t + c2 (x1t + x 2 )e −3 t
N
λ1 = λ2 = −3 < 0
t
0
A
Şekil 25 Negatif katlı reel öz değerlerin ( λ1 = λ2 = −3 ) sistem üzerindeki etkisi
Ç
A
L
I
Ş
M
Sonuçta, öz değerler katlı, reel ve negatif ise sistem kararlı davranır ( λi < 0 )