EME 3117 SİSTEM SİMÜLASYONU

9.1.2016
1
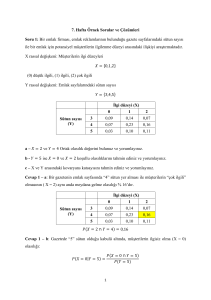
Rassal Sayı ve Rassal Değer Üretimi
EME 3117
2
SİSTEM SİMÜLASYONU
Girdi Analizi bölümünde gözlemlerden elde edilen
verilere en uygun dağılımı uydurmuştuk. Bu günkü
derste bu dağılımlardan simulasyonda kullanmak için
nasıl rassal değişken üretileceği üzerinde durulacaktır.
Rassal Sayı ve Rassal Değer
Üretimi
Örneğin bir eczaneye müşteri gelişleri arasında geçen
sürenin
Ders 10
dağılımı
belirlenmiş
olsun.
Arena’da
Bu
EXPO(30
dağılımdan
dk.)
olarak
simulasyonda
kullanacağımız gelişler arası süreler nasıl üretilebilir?
Rassal Sayı Üretimi
Rassal Sayı ve Rassal Değer Üretimi
3
4
Herhangi
bir
dağılımdan
rassal
bir
değişken
Bir simulasyonda kullanılan
gerçekte rassal değildir!
rassal
sayılar,
üretebilmek için U(0,1) rassal değişkenleri gereklidir.
Rassal sayılar, birbirinden bağımsız ve görülme
olasılıkları eşit olan sayıların oluşturduğu dizilerdir.
Bu sayı dizileri eşit olasılık gereği, Düzgün
Tanım:
Bir sözde rassal sayılar dizisi U(i), gerçek rassal
sayılar dizisi U(0,1)’deki bazı ilgili istatistiksel
özelliklere sahip deterministik sayılar dizisidir.
(Uniform) olasılık dağılımı gösterir.
1
9.1.2016
√Rassal Sayıların Özellikleri
Rassal Sayıların Dağılımı
6
Düzgün ve bağımsızlık özelliğinin iki sonucu;
1)(0,1) aralığı, eşit uzunlukta k sınıfa bölünürse, N;
gözlemlerin toplam sayısı olmak üzere, her
aralıktaki gözlemlerin beklenen değeri:
B=
N
k
2) Bir aralıkta bir değerin gözlemlenme olasılığı,
elde edilen bir önceki değerden bağımsızdır.
Rassal Sayı Üreteçlerinde İstenen Özellikler
7
1) Orta Kare Yöntemi
8
Bu yöntemde
i) (m) basamaklı ve genellikle tek olan bir sayı
başlangıç değeri (seed) olarak alınır.
ii) Bu sayının karesi alınarak bulunan sayının ortasındaki
m kadar basamaklı sayı alınır.
iii)Alınan bu sayı rassal sayı olarak kaydedilir.
iv)İstenen sayıda rassal sayı elde edene dek ii, iii, iv
tekrar edilir.
2
9.1.2016
2) Doğrusal Eşlik Üreteci
(Linear Congruential Generator)
Örnek
9
10
Tanım: Bir LCG aşağıda verilen tekrarlanan ilişkiye göre
belirlenen 0 ve m-1 arasındaki ( R0 , R1 , ) tam sayılar dizisi tanımlar:
X 0  5497 (Seed)
X 02   5497   30217009 ise X 1  2170
2
Ri 1   aRi  c  mod m
U1  0.2170
i  0,1, 2,...
R0 :
dizinin başlangıc değeri
: sabit çarpan katsayısı
: artış miktarı
m :modulus
X 12   2170   04708900 ise X 2  7089
2
a
c
U 2  0.7089
.
.
m, a, c, R0  tamsayı ve a  0 , c  0 ,
.
0  Ri  m  1
m  0,
ma,
mc
m  R0 ,
U i  Ri m
Çözüm
LCG Örnek
Ri +1 = ( aRi + c) mod m
i = 0,1,2,
( m= 8,a = 5,c = 1, R0 = 5)
12
(m = 8, a = 5, c = 1, R0 = 5) parametreli Doğrusal Eşlik Üreteç
(LCG) düsünün. Tanımlanan diziden ilk 9
hesaplayın.
Ri
ve
Ui
R1  (5 R0  1) mod 8  26 mod 8  2  U 1  0.25
değerlerini
• Rassal sayıların Ui=Ri/m R 2  (5R1  1) mod 8  11 mod 8  3  U 2  0.375
olduğuna dikkat edin.
R3  (5 R 2  1) mod 8  16 mod 8  0  U 3  0.0
R  (5 R  1) mod 8  1 mod 8  1  U 4  0.125
3
• Sayıların
çevrim 4
dizilerinde tekrarlanıp R5  6  U 5  0.75
tekrarlanmadığına
R6  7  U 6  0.875
dikkat edin.
R 7  4  U 7  0 .5
M od operatorü:
ê yú
z = y mod m Û z = y - mê ú
ë mû
ëxû , en büyük tamsayı
R8  5  U 8  0.625
• Uzun cevrim periyoduna
sahip a, m ve c R9  2  U 9  0.25
belirlenmesi amaçlanır.
£x
17
Örneğin, z = 17 mod 3 Û z = 17 - 3êê úú = 17 - 3 ´ 5 = 2 .
ë3û
3
9.1.2016
Rassal Sayı Dizileri
Rassal Sayılar Tablosu
13
14
R 0  5  R8
• Örneğin R1 =2 gibi bir çekirdek
(seed), bir rassal dizisinde
başlangıç yerini tanımlar.
• Rassal sayı dizisi, farklı
çekirdeklerle tanımlanan dizileri
gösterir.
• Farklı görevlerde bağımsız rassal
sayıları kullanabilmek için çevrimi
ayrı dizilere bölmek isteriz.
R7  4
R1  2
R6  7
R2  3
R3  0
R5  6
R4  1
16
Rassal Sayı Üreteçlerinin Testleri
EME 3105
15
• Kolmogorov-Smirnov Testi
SISTEM SIMÜLASYONU
• Ki-Kare Testi
• Bagimsizlik testleri
 Koşu
(run) testi
 Otokorlasyon
 Poker
Rassal Değer Üretimi
Ders 11
(Autocorrelation) testi
testi
4
9.1.2016
Amaç
Dağılımlardan Örneklem Alınması
• Bir simulasyon modelinde girdi olarak
kullanılmak üzere belirli bir dağılımdan
örneklem üretilmesi
• Tahmin edilemeyen yada belirsiz faaliyetlerin
modellenmesinde istatistiksel dağılımlar kullanılır.
• Yaygın olarak kullanılan rassal değer üretim
yöntemlerinin öğrenilmesi
• Gerçek yaşam problemlerindeki gelişler arası süre,
servis süreleri, talep vb. değişkenler genellikle
tahmin edilemezdir.


Ters dönüşüm tekniği
Kabul-ret tekniği
• Bu tür değişkenler, belli bir istatistiksel dağılıma
sahip rassal değişkenler olarak modellenebilir.
17
Rassal Değer Üretme Teknikleri
Ters Dönüşüm Tekniği
• Rassal değer üretme tekniklerinin tümü [0,1]
aralığında Düzgün dağılmış rassal sayıların elimizde
mevcut olduğunu varsayar.
Üstel, Düzgün, Weibull ve deneysel sürekli
Her bir Ri rassal sayı için:
dağılımların yanı sıra bir çok kesikli dağılımdan
örneklem almaya uygun bir yöntemdir.
Hesaplama yönünden basit ve direk bir yöntem
olmasına karşın, her zaman etkin değildir.
5
9.1.2016
Ters Dönüsüm Tekniği (Devam)
Uygulamalar
• Tekniğin temel mantığı:
r = F(x) birikimli dağılım fonksiyonu için
[0,1] düzgün dağılımından r rassal sayısını üret
 x’i hesapla.

• [a,b] aralığında Düzgün Değer Üretimi

F(x)
x=
F-1(r)
r = F(x)
• Üstel Değer Üretimi
r1
x1
x
22
[a,b] Aralığında Düzgün Değer Üretimi
[a,b] Aralığında Düzgün Değer Üretimi (Devam)
(Ters Dönüşüm)
(Ters Dönüşüm)
Düzgün dağılmış X rassal değişkenine ait f(x) olasılık
yogunluk fonksiyonu aşağıda verilmiştir.
ì 1
ï
f(x) = í b - a
ïî0
• X rassal değişkeninin Birikimli Dağılım Fonksiyonu
F(x), Olasılık Yogunluk Fonksiyonu f(x)’in integrali
alınarak bulunur.
a£ x£b
Aksi Halde
f(x): Olasılık Yoğunluk Fonksiyonu (Probability density function, pdf):
F(x) = ò
ì0
ïï x - a
f(x)dx = í
ïb - a
ïî1
x<a
a£ x£b
x>b
F(x): Birikimli (Olasılık) Dağılım Fonksiyonu (Cumulative density function, cdf)
6
9.1.2016
[a,b] Aralığında Düzgün Değer Üretimi
Üstel Dağılım (Ters Dönüşüm)
(Devam) (Ters Dönüşüm)
26
• Düzgün dağılımdan değerler üretmede ters dönüşüm
metodunu kullanmak için Fx(x) = R alınır ve x aşağıdaki
gibi çözülür:
ìl e- l x
f (x) = í
î0
xa
 R  x  F 1 ( x)  (b  a )  R  a
ba
ì0
F(x) = í
-lx
î1- e
• Artık, [a,b] aralığında Düzgün rassal değer üretebiliriz:
 [0,1] aralığında Düzgün R üret
 x = a + R (b -a)
E[X] =
1
l
25
Üstel Dağılım (Devam)
Üstel Dağılım (Devam)
(Ters Dönüşüm)
27
(Ters Dönüşüm)
28
1- İstenilen X rassal değişkeni için kümülatif yoğunluk fonksiyonu
hesaplanır.
Üstel Dağılım İçin:
üstel
7
x³0
A ksi Halde
x<0
0 £ x£¥
l=
1
E[X]
9.1.2016
Üstel Dağılım (Devam)
Üstel Dağılım (Devam)
(Ters Dönüşüm)
(Ters Dönüşüm)
29
30
Deneysel Kesikli Dağılım
Üstel Dağılım (Devam)
(Ters Dönüşüm)
(Ters Dönüşüm)
31
Üstel Dağılım için:
Üstel Birilimli Dağılım:
R
xi
1
2
3
f  xi  0.4 0.3 0.2
0.4 0.7 0.9
F x i 
if x  1
0
0.4 if 1  x  2

F ( x)  0.7 if 2  x  3
0.9 if 3  x  4

 1
if 4  x
4
1.0
X=4 (0.9 < R ≤ 1)
0.1
1.0
.8
X=3 (0.7 < R ≤ 0.9)
.6
X=2 (0.4 < R ≤ 0.7)
.4
X=1 (0 ≤ R ≤ 0.4)
.2
0
0
ters dönüşüm
8
1
2
3
4
xi
9.1.2016
Deneysel Kesikli Dağılım (Devam)
Rassal Normal Değer Üretme
(0,5<Rassal Sayı<1)
(Ters Dönüşüm)
Eğer Ri aralıktaysa
0 £ Ri £ 0.4
0.4 < Ri £ 0.7
0.7 < Ri £ 0.9
0.9 < Ri £ 1.0
xi
1
2
3
4

r = F(x) birikimli dağılım fonksiyonu için

[0,1] düzgün dağılımından r rassal sayısını üret

x’i hesapla.
s 2 = 100
Örnegin m =25,s 2 = 100 parametreli
Normal Dagilimdan rassal deger uretelim.
R=0.919 olsun.
F(x) = 0,919
Kesikli Ters Dönüşüm Algoritması
m = 25
(0,1) Düzgün dağılımdan rassal sayı ri üret.
x
z=
for i=1 to n
if ri  F(xi)
Rassal Değer=xi
end
end
x- m
s
x = m + zs
F(z) = 0,919
z
Rassal Normal Değer Üretme
Rassal Normal Değer Üretme
(0,5<Rassal Sayı<1)
(0<Rassal Sayı<0,5)
P( Z £ 1, 4 ) = 0,919
f(z)
Üretilen rassal sayının 0.5’ten küçük olması normal dağılımdan üretilecek
değerin ortalamadan küçük olduğunu gösterir.
z = 1, 4
z
s 2 = 100
x = m + zs
= 25 + 1, 4.10
= 39
Örnegin m =25,s 2 = 100 parametreli
Normal Dagılımdan rassal deger uretelim.
R=0.35 olsun.
m = 25
x
z=
x- m
s
F(x) = RS = 0, 35
s2 =1
F(z) = RS = 0,35
x = m - zs
9
-z
0
9.1.2016
Rassal Normal Değer Üretme
Rassal Normal Değer Üretme
(0<Rassal Sayı<0,5)
(0<Rassal Sayı<0,5)
P( Z £ 0.39 ) = 0,65
f(z)
P(Z £ -0.39) = 0, 35
s2 =1
-z
0
Þ
x = m - zs
0
z
P(Z < -z) = P(Z > z) = 0, 35
z
z = 0, 39
s2 =1
= 25 - 0, 39.10
z
= 21,1
0, 35
P(Z < z) = 1- 0, 35
= 0,65
Rassal Weibull Değer Üretme

Weibull Dağılımı için Birikimli Dağılım Fonksiyonu: F(x)=1-e
x
 
 

R=F(x)=1-e
x
 
 

e
x
 
 
 1 R

x
   ln e  ln 1  R 
 

x
    ln 1  R 
 
1/
  x  
  
   


   ln 1  R  
1/
1/
x
     ln 1  R  
 
x     ln 1  R  
1/
10