11 Nisan 2013 ITAP Resmi Sınavı
1. Kütlesi m=100g, hacmi V=200cm3 ve su ile dolu olan bir bardak, altı üste olarak ve açık
tarafı suya deyerek şekilde bir dinamometreye bağlıdır. Su bardaktan neden akmıyor ve
dinamometre kaç Newton göstermektedir?
A)1N
B)3N C)5N D)4N E)2N
2. Yüksekliği h, taban alanı S, kütlesi M olan bir silindir yoğunlukları ρ1 ve ρ2 ( ρ1 > ρ 2 ) olan
ρ − ρ2
M
h; ρ =
ρ1 − ρ 2
Sh
ρ / 2 − ρ2
M
E)
h; ρ =
Sh
( ρ1 − ρ2 )
ρ − ρ2
M
h; ρ =
ρ1 − ρ 2
Sh
ın
a
1 ρ − ρ2
M
h; ρ =
2 ρ1 − ρ 2
Sh
2ρ − ρ2
M
D)
h; ρ =
ρ1 − ρ 2
Sh
A)
vı
iki karışmayan sıvının sınırında yüzmektedir. Silindirin tabanı sıvıların yatay sınır yüzeyine
paraleldir. Silindir alt sıvıda ne kadar derinliğe batıyor?
C) 2
m
is
B)
⎛ 2m ⎞
D) ⎜1 +
⎟l
M ⎠
⎝
13
m ⎞
⎛
C) ⎜ 2 +
⎟l
2M ⎠
⎝
m ⎞
⎛
E) ⎜1 +
⎟l
⎝ 2M ⎠
20
m⎞
m⎞
⎛
⎛
A) ⎜ 2 + ⎟ l B) ⎜1 + ⎟ l
M⎠
⎝
⎝ M⎠
_2
.R
es
3. Kütlesi M olan bir lokomotif, doğrusal bir demir yolunda kütlesi m olan bir vagonu sabit
hızı ile çekmektedir. Bilinen bir anda vagonla lokomotif arasındaki bağlantı kopuyor ve vagon
bu andan duruncaya kadar l kadar yol alıyor. Bu sürede ise lokomotif ne kadar yol (L)
alacaktır? Lokomotifin uyguladığı kuvvet ve sürtünme kuvvet sabittir.
_F
O
O
_
4. Kütleleri m1 ve m2 ve hafif kütleli mükemmel bir iple bağlı olan iki cisim pürüzlü yatay bir
masa üstünde bulunmaktadır (şekildeki gibi). 1.cisimle
düzlüm arasındaki sürtünme kat sayısı m1, 2. ile ise m2
dir.1. cisme yatay bir dış kuvveti (F) uygulanmaktadır. İpin
gerilme kuvvetinin değerini bulunuz.
m1
mm
F + ( μ2 − μ1 ) 1 2 g
m1 + m2
m1 + m2
m2
mm
C) T =
F − ( μ1 − μ2 ) 1 2 g
m1 + m2
m1 + m2
m1
mm
F + ( μ1 − μ2 ) 1 2 g
E) T =
m1 + m2
m1 + m2
IT
AP
A) T =
m2
mm
F + ( μ1 − μ2 ) 1 2 g
m1 + m2
m1 + m2
m1
2m1m2
D) T =
F + ( μ1 − μ2 )
g
m1 + m2
m1 + m2
B) T =
5. Kütlesi M, uzunlu ise l olan bir tahtanın ucunda kütlesi m olan küçük bir kübik cisim
bulunmaktadır. Tahta ise pürüzsüz yatay bir masa üstündedir. Cisim, yönü tahtanın diğer
ucuna doğru, büyüklüğü ise F olan yatay bir kuvvet ile itilmektedir. Küp tahtanın diğer ucuna
ne kadar süre sonra varacaktır? Tahta ile cisim arasındaki sürtünme kat sayısı μ dur, küp
hareket sürecinde devrilmeyecektir.
A)
D)
2l
⎛F
m ⎞⎞
⎛
⎜ m − μ g ⎜1 + M ⎟ ⎟
⎝
⎠⎠
⎝
2l
⎛F
m
⎛
⎜ m + μ g ⎜1 + M
⎝
⎝
2l
B)
⎛F
⎛ 2m ⎞ ⎞
⎜ m − μ g ⎜1 + M ⎟ ⎟
⎝
⎠⎠
⎝
l
⎛F
m ⎞⎞
⎛
⎜ m + μ g ⎜1 + M ⎟ ⎟
⎝
⎠⎠
⎝
2l
E)
⎞⎞
⎟⎟
⎠⎠
C)
⎛ F
⎛ 2m ⎞ ⎞
⎜ 2m − μ g ⎜ 1 + M ⎟ ⎟
⎝
⎠⎠
⎝
is
ın
a
vı
6. Her birin kütlesi m olan 3 ağırlık ve 3 makara bir makara sistemi oluşturuyor (şekildeki
gibi). A ve B makaraları yatay sabit bir ortak dingile sabit olarak
tutturulmaktadır. C makara ve ip hafif kütleli, ip mükemmel, ip ile makaralar
arasında ise sürtünme yoktur. Cisimlerin ivmelerini bulunuz.
ω0 R
1
E;
2
1
Q = E;
4
1
Q = E;
3
1
Q = E;
2
3
Q = E;
4
; Q=
IT
AP
2
ωR
B) v = 0 ;
4
ωR
C) v = 0 ;
3
D) v = ω0 R;
E) v =
ω0 R
8
;
1
E;
4
2
Er = E;
4
2
Er = E ;
9
1
Er = E;
4
1
Er = E;
8
Er =
_F
A) v =
O
O
_
20
13
_2
.R
es
m
2g
2g
2g ⎫
g
g
g⎫
⎧
⎧
; a2 =
; a3 = − ⎬
A) ⎨a1 = ; a2 = ; a3 = − ⎬
B ⎨a1 =
3
3
3 ⎭
2
2
2⎭
⎩
⎩
g
g
g⎫
g
g
g⎫
⎧
⎧
C) ⎨a1 = ; a2 = ; a3 = − ⎬
D) ⎨a1 = − ; a2 = − ; a3 = ⎬
3
3
3⎭
3
3
3⎭
⎩
⎩
2g
2g
2g ⎫
⎧
; a2 = −
; a3 = − ⎬
E) ⎨a1 = −
3
3
3 ⎭
⎩
7. Kütlesi m, yarıçapı R ince bir çembere dikey düzlemde ω0 açısal bir hız kazandırılıyor kütle
merkezin hızı sıfır olar şekilde bir yatay düzlemde bırakılıyor. Çember durgun hareket haline
geldiğinde merkezin hızı ne kadar olacaktır? Çember ile zemin arasında bilinen bir sürtünme
var olduğunu sayınız. Sistemin ilk kinetik enerjisi geçiş sürenin sonunda nasıl bir şekilde
dağılmış olacaktır? Kaçta kaçı ısıya (Q), dönme (Er) ve öteleme (Etr) kinetik enerjisine
dönecektir?
1
E
4
1
Etr = E
4
4
Etr = E
9
1
Etr = E
4
1
Etr = E
8
Etr =
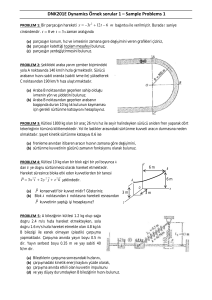
8. Bir araba parabolik şeklinde olan bir köprüde v=54km/h sabit hızı ile hareket etmektedir.
Köprünün yüksekliği h=5m, yatay doğrultuda uzunluğu ise l=60m dir. Araba köprünün tepe
noktasında iken köprüye uyguladığı kuvvet arabanın normal ağırlığının kaç katıdır?
A)0.65
B)0.75
C)0.85
D)0.95
E)0.45
9. Jüpiter gezegenin yarıçapı RJ = 7 ⋅104 km dir. Onun etrafında dönen satelitlerden birinin
yörüngesi neredeyse çembersel ve yarıçapı r = 106 km , periyotu ise T=7.15 gündür. Bu
verilere göre Jüpiter için birinci (v1) ve ikinci (v2) uydu hızını bulunuz (yani bir cismin
Jüpiter’in yer çekim alanından kurtulmak için gereken minimum hız).
B) v1 = 7.4(km / s ); v2 = 10.5(km / s )
D) v1 = 11.4(km / s ); v2 = 16.1(km / s )
ın
a
vı
A) v1 = 38.4(km / s ); v2 = 54.3(km / s )
C) v1 = 28.4(km / s ); v2 = 40.2(km / s )
E) v1 = 18.4(km / s ); v2 = 26.0(km / s )
.R
es
m
is
10. Kütlesi m=100kg olan bir astronot, kütlesi M=10ton olan bir uyduya uzunluğu l=64m olan
hafif kütleli bir halat ile bağlı olup, açık kozmosa çıkıyor. Gerilmiş halat uydunun ve
Dünyanın merkezinden geçen doğrultunun boyuncadır ve uydu astronot ile Dünyanın arasında
bulunmaktadır. Udunun yörüngesi, yarıçapı R=6400km olan bir çember olduğuna göre halatın
gerilme kuvvetinin değeri ne kadardır? Uydunun yörüngesinde yer çekim ivmesini
g = 10m / s 2 olarak alınız. Udunun boyu l’den çok daha küçük olduğunu kabul ediniz.
1 −2
1
⋅10 N E) ⋅10−2 N
2
3
11. Uzunlukları ve yay sabitleri sırasıyla l1, l2, k1 ve k2 olan hafif kütleli yaylardan biri diğer
yayın içinde bulunmaktadır. Yayların uçları bağlıdır (‘paralel’ bağlantı) ve yaylar bir birine
deymemektedir. Olaşan yay sistemin etkin yay sabitini (k) bulunuz.
C) 2 ⋅10−2 N
D)
_2
B) 3 ⋅10−2 N
( k1 + k2 )
20
13
A) 1 ⋅10−2 N
k1k2
2k1k2
E)
D) k1 + k2
k1 + k2
k1 + k2
2
12. Her birinin kütlesi m olan iki küre yay sabiti k olan hafif kütleli bir yayla bağlıdır. Bu
sistem v0 hızı ile şekildeki gibi hareket ederken ona özdeş,
hareketsiz olan başka bir sistem ile çarpışıyor ve çarpışan
küreler merkezi ve esnek çarpışma ediyor. Kürelerin
çarpışmanın hemen ardından ve uzun süre sonra hızlarını
v1,v2,v3 ve v4 (sıralama soldan sağıya doğrudur) bulunuz.
Çarpışma süresi sistemin titreşim periyotundan çok daha düşük, yayın serbest uzunluğu ise
k
l v0
olduğunu varsayınız. Yer çekim yoktur.
m
_
B) 2 ( k1 + k2 ) C)
IT
AP
_F
O
O
A)
v
v
⎧
⎫
Çarpışmanın hemen ardından ⎨ v1 = 0 ; v 2 = 0; v 3 = 0 ; v 4 = 0 ⎬
2
2
⎩
⎭
A)
v
v ⎫
⎧
Çarpışmadan uzun süre sonra ⎨ v1 = 0; v 2 = 0; v 3 = 0 ; v 4 = 0 ⎬
2
2⎭
⎩
Çarpışmanın hemenardından { v1 = v 0 ; v 2 = 0; v 3 = v 0 ; v 4 = 0}
B)
Çarpışmadan uzun süre sonra { v1 = 0; v 2 = 0; v 3 = v 0 ; v 4 = v 0 }
v
v
⎧
⎫
Çarpışmanın hemen ardından ⎨ v1 = − 0 ; v 2 = 0; v 3 = − 0 ; v 4 = 0 ⎬
2
2
⎩
⎭
C)
v
v ⎫
⎧
Çarpışmadan uzun süre sonra ⎨ v1 = 0; v 2 = 0; v 3 = 0 ; v 4 = 0 ⎬
2
2⎭
⎩
Çarpışmanın hemenardından {v1 = 2 v 0 ; v 2 = 0; v 3 = 2 v 0 ; v 4 = 0}
D)
Çarpışmadan uzun süre sonra {v1 = 0; v 2 = 0; v 3 = 2 v 0 ; v 4 = 2 v 0 }
ın
a
vı
v
v
⎧
⎫
Çarpışmanın hemen ardından ⎨ v1 = 0 ; v 2 = 0; v 3 = 0 ; v 4 = 0 ⎬
3
3
E)
⎩
⎭
Çarpışmadan uzun süre sonra { v1 = 0; v 2 = 0; v 3 = v 0 ; v 4 = v 0 }
B)5522m
C)7733m
D)4422m
E)3333m
.R
A)6622m
es
m
is
13.Yatay bir zeminde bulunan bir top, yataya göre 450 açıyla ateş etmektedir. Ateşten 15s
sonra ateş edilen bir gülle yörüngesinin tepe noktasında kütleleri eşit olan iki parçaya patlıyor.
Parçalardan biri zemine tamamen patlama noktasının altında, patlamadan 15s sonra düşüyor.
Güllenin ikinci parçası zemine toptan ne kadar uzaklıkta düşecektir?
20
13
_2
14. Kütleleri aynı olan iki vagon raylar üstünde bulunmaktadır ve bir biriyle ince, hafif kütleli
halatla bağlıdır. Halatın uçları vagonların dingillerine bağlıdır. Her bir dingilin çapı d dir
1.vagonun dingili bir motora bağlıdır. Vagonlar ilk anda hareketsizdir ve bilinen bir anda
motor çalışmaya başlıyor ve halatı sabit ω açısal hızı ile dingile sarmaya başlıyor. Halatın
sarma döngüsünün çapı dingilin çapına eşittir. Vagonlarla raylar arasında kayma yok, halat
esnemez. Bu verilere göre vagonların yere göre hızını bulunuz.
_
g
1 g 2
g
1 g 2
x; y yerli = h0 x
B) yuçaktan = h0 + x; y yerli = h0 x
2
a
a
2v
2 v2
g
1 g 2
g
g
x
D) yuçaktan = 2 x; y yerli = h0 - 2 x 2
C) yuçaktan = - x; y yerli = h0 2
a
a
2v
v
1g
1 g 2
E) yuçaktan = x; y yerli = −h0 x
2a
2 v2
15. 100m arayı 10 saniyede koşan bir sporcu, aranın ilk 10m’sini sabit a ivme ile diğer
kısmını ise sabit v hızı ile koşmaktadır. v ile a’yi bulunuz.
IT
AP
_F
O
O
A) yuçaktan =
A) 13(m / s ) ve 4.05(m / s 2 )
B) 9(m / s ) ve 7.05(m / s 2 )
C) 12(m / s ) ve 4.05(m / s 2 )
D) 11(m / s ) ve 6.05(m / s 2 )
E) 12(m / s ) ve 5.05(m / s 2 )
16. Kesit alanı S olan, yalıtılmış dikey bir silindirde, kütlesi M olan bir piston altında 1mol
miktarda tek atomlu bir ideal gaz bulunmaktadır. Gaz içinde direnci r olan bir ısıtıcı emk’sı ε,
iç derencini ise sıfır olan bir elektrik kaynağına bağılıdır. Piston üstünde hava basıncı p0
eşittir. Pistonun yükselme hızını bulunuz.
A)
E)
2
ε2
3 r ( p0 + Mg )
B)
2
ε2
5 r ( p0 + Mg )
C)
5
ε2
2 r ( p0 + Mg )
D)
3
ε2
2 r ( p0 + Mg )
ε2
r ( p0 + Mg )
17. Su ile dolu olan büyük bir kap içine, sıcaklıkları aynı ve çok büyük, aynı metalden
yapılmış küreler arka arkaya atılıyor. Yarıçapı r1 = 0.5cm olan küre suyun sıcaklığını
A) 4.50 C
B) 5.50 C
C) 3.50 C
D) 6.50 C
E) 2.50 C
ın
a
vı
Δt1 = 0.50 C , yarıçapı r1 = 1cm olan ise Δt2 = 1.20 C kadar artırıyor. Bu verilere göre yarıçapı
r3 = 1.5cm olan küre suyun sıcaklığını ne kadar artıracaktır?
13
_2
.R
q1 q3
1 q2 q3
1 q3 q2 ⎞
T
T
=
=
;
;
⎟
2
3
4πε 0 l12
4πε 0 l12 ⎠
l22
q1 q2
1 q2 q3
1 q3 q1 ⎞
; T2 =
; T3 =
⎟
2
2
4πε 0 l1
4πε 0 l22 ⎠
l3
q2 q3
1 q1 q3
1 q1 q2 ⎞
; T2 =
; T3 =
⎟
2
2
4πε 0 l2
4πε 0 l32 ⎠
l1
20
⎛
1
A) ⎜ T1 =
4πε 0
⎝
⎛
1
B) ⎜ T1 =
4πε 0
⎝
⎛
1
C) ⎜ T1 =
4πε 0
⎝
es
m
is
18. Yükleri q1, q2 ve q3 olan üç noktasal yük bir biriyle iplerle bağlıdır: 1. ve 2. yükü
bağlayan ipin uzunluğu l3, 2. ve 3. l1 ve 3. ile 1. uzunluk l2 dir. Sistem dengededir ve yer
çekim yoktur. İplerin gerilme kuvvetlerini (T) bulunuz.
IT
AP
_F
O
O
_
⎛
1 q2 q3
1 q1 q3
1 q1 q2 ⎞
D) ⎜ T1 =
; T2 =
; T3 =
⎟
2
2
4πε 0 l2
4πε 0 l3
4πε 0 l12 ⎠
⎝
⎛
1 q2 q3
1 q1 q3
1 q1 q2 ⎞
E) ⎜ T1 =
;
T
;
T
=
=
⎟
2
3
2πε 0 l12
2πε 0 l22
2πε 0 l32 ⎠
⎝
19. Yükleri q ve 2q olan iki yalıtılmış metalik cisim ince bir telle bağlanır ve yükleri sırasıyla
2q ve q oluyor. Eğer ilk başta cisimlerin yükleri 5q ve -2q olsaydı, cisimler telle bağladıktan
sonra yükleri ne kadar olacaktı? Deneyde kürelerin konumları aynı kalıyor.
A) ( Q1 = 2q; Q2 = q )
B) ( Q1 = − q; Q2 = 3q )
D) ( Q1 = 6q; Q2 = −3q )
E) ( Q1 = q; Q2 = 2q )
C) ( Q1 = −2q; Q2 = 5q )
20. Uzunluğu l olan metalik bir çubuk, arasındaki mesafe L, yükleri ise +Q ve –Q olan, iki
yüklerin ortasında, yükleri bağlayan doğru boyunca yerleştiriliyor. Düşünerek çubuğu iki
yarıya bölelim. Her bir yarının yükü yaklaşık ne kadardır?
l
A) Q
L
l2
C) Q 2
L
l
B) 2Q
L
D) Q
l2
(L + l)
E) Q
2
l
L+l
C)(a)0.8; (b)0.5J
D)(a)0.5; (b)0.5J
ın
a
B)(a)0.5; (b)0.8J
is
A)(a)0.8; (b)0.8J
E)(a)0.9; (b)0.5J
vı
21. Elimizde, her birinin gerilimi ε=1V, iç direnci ise r=1Ω iki elektrik kaynağı ve her birinin
direnci R=1Ω olan iki direnç bulunmaktadır. (a)Kaynağın verimi en büyük olması için ve
(b)dış dirençlerde açığa en fazla ısı verilmesi için kaynaklar ve dirençler nasıl bir şekilde
bağlanmalıdır?
4
ε;
5
2
ε;
3
1
ε
5
1
ε
3
1
1 1
C) Cε 2 ; ε ; ε
4
2 2
20
13
1 2
34
Cε ; ε ; 0
B) Cε 2 ;
2
25
5
1 2
5
Cε 2 ;
D) Cε 2 ; ε ; ε E)
18
3 3
18
A)
_2
.R
es
m
22 Şekildeki devrede depolanan enerjiyi ve kondansatörlerin
gerilimini bulunuz. İlk başta anahtar K1 kapatılıyor, ardından
anahtar K2 kapatılıyor ve sonrası açılıyor.
O
O
_
23. Sığası C olan bir kondansatör U gerilime kadar yükleniyor, ardından sığası C olan başka
bir kondansatör ilk kondansatörle paralel olarak bağlanıyor. Sistem dengeye geldiğinde
kondansatörlerin gerilimini ve sistemin enerji değişimini bulunuz.
U
U
1
; 0
B) ; − CU 2
2
2
4
U 1
E) ; CU 2
2 4
IT
AP
_F
A)
C)
U 1
; - CU 2
2 8
D)
U 1
; CU 2
2 8