ORTA ÖĞRETİM 9. SINIF GEOMETRİ DERSİ

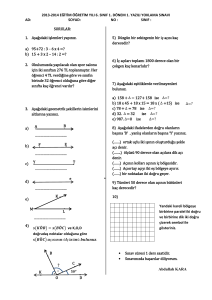
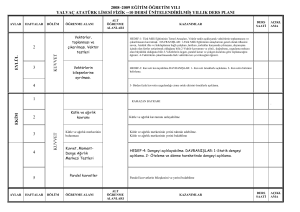
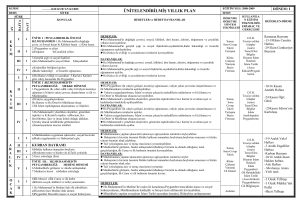
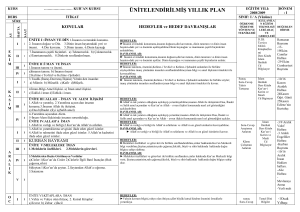
ORTA ÖĞRETİM 9. SINIF GEOMETRİ DERSİ ÖĞRETİM PROGRAMI
1. BÖLÜM : GEOMETRİK KAVRAMLAR
Amaç-1: Nokta, Doğru, Düzlem, Işın ve Uzayı Kavrayabilme.
DAVRANIŞLAR:
1.Nokta, doğru, düzlem ve uzay kavramlarını açıklama.
2.Farklı iki noktadan geçen doğru sayısını söyleme ve yazma.
3.Doğrusal ve düzlemsel noktalar kümesini tanımlama.
6.İki nokta arasındaki uzaklığı tanımlama.
7.Arada olmayı tanımlama.
8.Doğru parçasını tanımlama.
9.Işını tanımlama.
Amaç-2: Nokta, Doğru ve Düzlem ile İlgili Uygulama Yapabilme.
DAVRANIŞLAR:
1. Koordinatları verilen iki nokta arasındaki uzaklığı hesaplama.
2. Koordinatları verilen ve doğrusal olan üç noktadan arada olanı bulma ve yazma.
3. Uç noktalarının koordinatları verilen bir doğru parçası üzerinde bulunan ve verilen
özellikleri sağlayan noktaların koordinatlarını bulma ve yazma.
4. Uç noktalarının koordinatları verilen bir doğru parçasının orta noktasının koordinatını
bulma ve yazma.
5. Uç noktalarının biri ile orta noktasının koordinatı verilen doğru parçasının diğer uç
noktasının koordinatını bulma ve yazma.
6. Verilen bir [AB ışını üzerinde |AX|=k , (k=l,2,3,4,5) olacak biçimde X noktalarını
bulup işaretleme.
Amaç-3: Nokta, Doğru ve Düzlem Arasındaki İlişkileri Kavrayabilme.
DAVRANIŞLAR:
1. Doğrusal (doğrudaş) olmayan farklı üç noktadan geçen düzlem sayısını söyleme ve
yazma.
2.
3.
4.
5.
6.
7.
8.
9.
Bir doğrunun bir düzlemin içinde olmasını tanımlama.
Paralel doğruları tanımlama.
Paralellik aksiyomunu söyleme ve yazma.
Doğru ile düzlemin birbirine göre konumlarını söyleme ve yazma.
Bir doğru ile dışındaki bir noktayı içeren düzlem sayısını açıklama.
Kesişen iki doğruyu içeren düzlem sayısını açıklama.
Kesişen iki düzlemin arakesitini söyleme ve yazma.
İki düzlemin birbirine göre konumlarını söyleme ve yazma.
Amaç-4: Nokta, Doğru ve Düzlem ile İlgili Uygulama Yapabilme.
DAVRANIŞLAR:
1. "İki noktadan bir doğru geçer" aksiyomuna çevreden uygun örnekler söyleme
2. Verilen paralel iki doğruyu içeren düzlem sayısını söyleme ve yazma.
3. "Doğrusal olmayan farklı üç noktadan bir düzlem geçer" aksiyomuna çevreden uygun
örnekler söyleme.
1 Amaç-5: Açı ile İlgili Temel Kavramları Kavrayabilme.
DAVRANIŞLAR:
1. Açıyı tanımlama.
2. Bir açının yönünü açıklama.
3. Açı ölçüsü birimlerinden dereceyi çember yayı yardımı ile tanımlama.
4. Bir açının ölçüsünü tanımlama.
5. Dik açıyı tanımlama.
6. İki doğrunun dikliğini tanımlama.
7. Dar açıyı tanımlama.
8. Geniş açıyı tanımlama.
9. Bir açının dikler (tümler) açısını tanımlama.
10. Bütünler açılan tanımlama.
11. Tam açıyı tanımlama.
12. Eş açıları tanımlama.
13. Paralel iki doğruyu üçüncü bir doğru kestiğinde oluşan açılar arasındaki ilişkiyi
söyleme ve yazma
14. Karşılıklı olarak kenarları paralel iki açının ölçüleri arasındaki bağıntıları söyleme ve
gösterme.
15. Karşılıklı olarak kenarları dik iki açının ölçüleri arasındaki bağıntıları söyleme ve
gösterme.
16.Bir açının açıortayını tanımlama, özelliklerini söyleme ve yazma.
Amaç-6: Açılar ile İlgili Uygulama Yapabilme.
DAVRANIŞLAR:
1. Açı çeşitlerine çevreden uygun örnekler gösterme.
2. Verilen bir açıya eş bir açıyı pergel ve cetvel kullanarak çizme.
3. Verilen bir dar açının dikler açısını bulma.
4. Verilen bir açının bütünler açısını bulma.
5. Komşu bütünler iki açının açıortayları arasındaki ilişkiyi söyleme ve gösterme.
2. BÖLÜM: DOĞRUNUN ANALİTİK İNCELENMESİ
Amaç-1: Analitik Düzlemde Uzaklığı Kavrayabilme.
DAVRANIŞLAR:
1. Analitik düzlemin noktaları ile reel sayı ikilileri arasındaki ilişkiyi söyleme ve yazma.
2. Analitik düzlemin iki noktası arasındaki uzaklığı, bu noktaların koordinatları
cinsinden veren bağıntıyı bulma.
3. Bir doğru parçasının orta noktasının koordinatlarını, uç noktalarının koordinatları
cinsinden veren bağıntıyı bulma.
4. Bir doğru parçasını verilen bir oranda bölen noktaları bulma.
Amaç-2. Analitik Düzlemde Uzaklık ile İlgili Uygulama Yapabilme.
DAVRANIŞLAR:
1. Koordinatları verilen bir noktayı analitik düzlemde bulup işaretleme.
2. Koordinatları verilen iki nokta arasındaki uzaklığı bulma.
4. Verilen bir doğru parçasının orta noktasını bulma.
2 Amaç-3: Analitik Düzlemde Doğru Denklemini Kavrayabilme.
DAVRANIŞLAR:
1. Dik üçgende bir açının tanjantını tanımlama.
2. Eksen çember yardımıyla, geniş açıların trigonometrik oranlarını, dar
açıların trigonometrik oranlan cinsinden hesaplama.
3. Ölçüsü 30° , 45° , 60° , 90° veya bunlardan birisinin herhangi bir katı olan açının
tanjantını söyleme ve yazma.
4. Bir doğrunun eğim açısını ve eğimini tanımlama.
5. Bir noktası bilinen doğrunun eğimini veren bağıntıyı bulma.
6. İki doğrunun paralel olma şartını açıklama.
7. İki doğrunun dik olma şartını açıklama.
8. Eğimi ve bir noktası bilinen doğrunun denklemini bulma.
9. İki noktası bilinen doğrunun denklemini bulma.
10. Koordinat eksenlerine paralel olan doğruların eğimlerini söyleme ve yazma.
11. Koordinat eksenlerine paralel olan doğruların denklemlerini söyleme ve yazma.
12. D={(x,y) | y=mx+n, m,n ∈ R, (x,y) ∈ RxR} kümesini analitik düzlemde gösterme.
13. ax+by+c=0 biçimindeki bir denklemin düzlemde bir doğru temsil ettiğini (a,b,c' nin
alacağı değerlere göre irdeleyerek) gösterme.
14. Eksenleri kestiği noktalar verildiğinde, doğrunun denklemini bulma.
15. İki doğrunun kesişme noktasının koordinatlarını bulma.
16. İki bilinmeyenli denklem sisteminin çözüm kümesini analitik düzlemde yorumlama.
17. Kesişen iki doğrunun oluşturduğu açının ölçüsünü veren bağıntıyı bulma. 18. Bir noktanın bir doğruya olan uzaklığını veren bağıntıyı bulma.
Amaç-4: Doğrunun analitik incelenmesi ile ilgili uygulama yapabilme.
DAVRANIŞLAR:
1. Bir noktası ve eğimi verilen doğrunun denklemini bulma ile ilgili problem çözme.
2. İki noktası verilen doğrunun denklemini bulma ile ilgili problem çözme.
3. Koordinat eksenlerinin denklemlerini söyleme ve yazma.
4. Eğim açısı 30° , 45° , 60° ,90° veya bunlardan birisinin belli bir katı olarak verilen
doğrunun eğimini söyleme ve yazma.
5. Koordinat eksenlerinin oluşturduğu açıların açıortay doğrularını bulma.
6. Verilen bir noktadan geçen ve eksenlere paralel olan doğruların denklemini yazma.
7. Bir doğrunun denklemi verildiğinde eğimini bulma.
8. Denklemleri verilen iki doğrunun birbirine göre durumlarını belirleme ile ilgili
problem çözme.
9. Denklemleri verilen iki doğrunun kesişim noktasını bulma.
10. Verilen iki bilinmeyenli lineer denklem sisteminin çözüm kümesinin varlığını
analitik düzlemde irdeleme ve varsa çözüm kümesini bulma.
11. Köşelerinin koordinatları verilen bir üçgenin kenarlarını ve yüksekliklerini taşıyan
doğruların denklemlerini bulma.
12. Verilen noktalar ve doğrular arasındaki uzaklıkları bulma ile ilgili problem
çözme.
3 3. BÖLÜM: ÜÇGENLER
Amaç-1: Üçgen ile İlgili Temel Kavramları Kavrayabilme.
DAVRANIŞLAR:
1. Çokgeni tanımlama.
2. Özel bir çokgen olarak üçgeni tanımlama.
3. Üçgen çeşitlerini söyleme ve yazma.
4. Bir üçgenin yardımcı elemanlarını tanımlama (Kenarortay, açıortay, yükseklik).
9. Bir üçgende, kenarlar ile açılar arasındaki ilişkiyi söyleme ve gösterme.
10.Bir üçgende kenar uzunlukları arasındaki bağıntıları söyleme ve yazma (üçgen
eşitsizliği).
Amaç-2: Üçgenlerin Elemanları ile İlgili Uygulama Yapabilme.
DAVRANIŞLAR:
1.Verilen bir ikizkenar üçgende tabana ait kenarortayın özelliklerini söyleme ve
gösterme.
3.Kenar uzunlukları verilen bir üçgenin açılarının ölçüleri arasındaki sıralamayı söyleme
ve yazma.
4.İki kenar uzunluğu verilen bir üçgenin, üçüncü kenar uzunluğunun alabileceği değerler
kümesini söyleme ve yazma.
5.Verilen bir dik üçgende hipotenüse ait kenarortay ile hipotenüs arasındaki ilişkiyi
söyleme ve gösterme.
6.Bir açısının ölçüsü 30° olan bir dik üçgende, kenar uzunlukları arasındaki bağıntıyı
söyleme ve yazma.
7.Verilen bir üçgende bir dış açı ile bu dış açıya komşu olmayan iç açılar arasındaki
bağıntıyı söyleme ve gösterme.
8.Bir üçgenin iç açılarının ölçüleri toplamını söyleme ve gösterme.
(Üçgenlerde benzerlik bölümünden )
Amaç-3: Dik Üçgenlerde Metrik Bağıntıları Kavrayabilme.
DAVRANIŞLAR:
1. Bir dik üçgende Pisagor teoremini söyleme ve gösterme.
2. Bir dik üçgen ile bu üçgenin hipotenüsüne ait yüksekliğin oluşturduğu üçgenler
arasındaki ilişkiyi söyleme ve gösterme.
3. Bir dik üçgende yükseklik bağıntısını söyleme ve gösterme.
4. Bir dik üçgende dik kenar bağıntısını söyleme ve gösterme.
Amaç-4: Dik Üçgenlerde Metrik Bağıntılar ile Uygulama Yapabilme.
DAVRANIŞLAR:
1. Bir dik üçgende hipotenüse ait yüksekliğini hipotenüsten ayırdığı doğru parçalarının
uzunlukları verildiğinde, üçgenin diğer elemanlarının uzunluğunu bulma.
2. Bir dik üçgende dik kenarlar, yükseklik ve yüksekliğin hipotenüs üzerinde ayırdığı
parçalardan herhangi ikisinin uzunluğu verildiğinde diğerlerinin uzunluklarını bulma.
4 4. BÖLÜM :ÇEMBER
Amaç-1: Çember ile İlgili Temel Kavramları Kavrayabilme.
DAVRANIŞLAR:
1. Çember, çap, yarıçap, merkez, kesen, kiriş, teğet ve normali tanımlama.
2. Çemberin iç ve dış bölgelerini tanımlama.
3. İki çemberin eşliğini tanımlama.
4. Aynı düzlem içindeki bir doğru ile bir çemberin birbirine göre konumlarını
açıklama.
5. Çemberde kirişin özelliklerini gösterme.
6. Çemberde teğetin özelliklerini gösterme.
7. Aynı düzlemdeki iki çemberin birbirine göre konumlarını açıklama.
Amaç-2: Çembere İlişkin Temel Kavramlarla İlgili Uygulama Yapabilme.
DAVRANIŞLAR:
1. Yarıçap uzunluğu verilen bir çemberin merkezinden belli bir uzaklıktaki
kirişin uzunluğunu bulma.
2. Verilen bir çemberde merkezden aynı uzaklıktaki kirişlerin uzunlukları
arasındaki ilişkiyi gösterme.
3. Dıştan (veya içten) teğet olarak verilen iki çemberin, merkezleri ile değme
noktası arasındaki ilişkileri gösterme.
Amaç-3: Çemberde Yay ve Açılar ile İlgili Temel Kavramları Kavrayabilme.
DAVRANIŞLAR:
1. Merkez açıyı tanımlama.
2. Çemberde küçük yay ve büyük yay ile ölçülerini tanımlama.
3. Çemberde iki yayın eşliğini tanımlama.
4. Çemberde merkez açının ölçüsü ile gördüğü yayın ölçüsü arasındaki bağıntıyı
yazma.
5. Çevre açıyı tanımlama.
6. Çevre açı ile gördüğü yayın ölçüsü arasındaki bağıntıyı gösterme.
7. Teğet-kiriş açıyı tanımlama.
8. Teğet-kiriş açının ölçüsü ile gördüğü yayın ölçüsü arasındaki bağıntıyı gösterme.
9. Aynı yayı gören merkez, çevre ve teğet-kiriş açılar arasındaki bağıntıları gösterme.
10. Tam açıyı tanımlama.
11 . İç açıyı tanımlama.
12.Bir açının ölçüsü ile kolları (kenarları) arasında kalan yayların ölçüleri arasındaki
bağıntıyı gösterme.
13.Dış açıyı tanımlama.
14.Bir dış açının ölçüsü ile kolları (kenarları) arasında kalan yayların ölçüleri arasındaki
bağıntıyı gösterme.
15.Çemberin uzunluğunu yazma.
l6.Bir merkez açının gördüğü yayın uzunluğunu yazma.
5 Amaç-4: Çemberde Yay ve Açılara İlişkin Temel Kavramlarla İlgili Uygulama
Yapabilme.
DAVRANIŞLAR:
1. Aynı yayı gören merkez, çevre, teğet-kiriş açılardan biri verildiğinde diğerlerini
bulma.
2. Merkez (veya çevre) açının gördüğü yayın ölçüsü verildiğinde açının ölçüsünü
yazma.
3. Bir iç açının ölçüsü ile kolları arasında kalan yaylardan birinin ölçüsü verildiğinde
diğer yayın ölçüsünü bulma.
4. Bir dış açının ölçüsü ile kollan arasında kalan yaylardan birinin ölçüsü verildiğinde
diğer yayın ölçüsünü bulma.
5. Yarıçap uzunluğu ile merkez açının gördüğü yayın uzunluğu verildiğinde merkez
açının ölçünü bulma.
5. BÖLÜM: KATI CİSİMLER ALAN VE HACİMLERİ
Amaç-1: Prizmayı, Özelliklerini ve Çeşitlerini Kavrayabilme.
DAVRANIŞLAR:
1. Prizmayı tanımlama.
2. Prizmanın tabanlarını tanımlama.
3. Prizmanın taban ayrıtlarını tanımlama.
4. Prizmanın yan yüzlerini tanımlama.
5. Prizmanın yan ayrıtlarını tanımlama.
6. Prizmanın yüksekliğini tanımlama.
11.Dik prizmayı tanımlama.
13.Düzgün prizmayı tanımlama.
14.Paralelyüzü tanımlama.
15.Dikdörtgenler prizmasına tanımlama.
16. Küpü tanımlama.
17. Tabanlarına göre prizmaları adlandırma.
18. Dikdörtgenler prizmasının cisim köşegeni ile bir köşeden çıkan ayrıtlar
arasındaki bağıntıyı söyleme ve gösterme.
Amaç-2: Prizmaların Alan ve Hacimlerini Kavrayabilme.
DAVRANIŞLAR:
1. Dik prizmanın yanal alanını veren bağıntıyı söyleme ve gösterme.
3. Prizmanın toplam alanını veren bağıntıyı söyleme ve gösterme.
4. Dik prizmanın hacmini veren bağıntıyı söyleme ve gösterme.
Amaç-3: Prizmaların Alan ve Hacimleri ile İlgili Uygulama Yapabilme.
DAVRANIŞLAR:
1. Tabanı yamuk olan bir dik prizmanın taban kenarları ile yüksekliği
verildiğinde yanal alanını bulma.
2. Yüksekliği ile tabanının kenarları verilen bir dik prizmanın yanal alanını
bulma
6 3. Yanal alanı ile tabanının çevresi verilen bir dik prizmanın yüksekliğini
bulma.
4. Tabanının bir kenarı ile yüksekliği verilen eşkenar üçgen dik prizmanın
toplam alanını ve hacmini bulma.
5. Cisim köşegeninin uzunluğu verilen bir kübün toplam alanını ve hacmini
bulma.
Amaç-4: Piramitleri, Alan ve Hacimlerini Kavrayabilme. DAVRANIŞLAR:
1. Piramidi tanımlama.
2. Piramidin tepe noktasını, tabanını; yan ayrıtlarını, yüksekliğini, yanyüz
yüksekliğini tanımlama.
3. Düzgün piramidi tanımlama.
4. Düzgün dörtyüzlüyü tanımlama.
7.Bir dik piramidin hacmini veren bağıntıyı söyleme ve gösterme.
8.Düzgün piramidin yanal alanını veren bağıntıyı söyleme ve gösterme.
Amaç-5: Piramitlerin Alan ve Hacimleri ile İlgili Uygulama Yapabilme.
DAVRANIŞLAR:
2.Tabanının bir kenarı ile yüksekliği verilen düzgün kare dik piramidin yanal alanını,
toplam alanını ve hacmini bulma.
Amaç-6: Dairesel Silindiri, Alan ve Hacmini Kavrayabilme.
DAVRANIŞLAR:
1. Silindiri tanımlama.
2. Dik dairesel silindiri tanımlama.
4.Dik dairesel silindirin yüksekliğini tanımlama.
6.Dik dairesel silindirin yanal alanını veren bağıntıyı gösterme.
7.Dik dairesel silindirin hacmini veren bağıntıyı söyleme ve yazma.
Amaç-7 : Dairesel Silindirin Alan ve Hacmi ile İlgili Uygulama Yapabilme.
DAVRANIŞLAR:
1. İç ve dış çapları ile yüksekliği verilen dik dairesel silindir biçimindeki bir
borunun dolgu kısmının hacmini hesaplama.
2. İç ve dış çaplan ile yüksekliği verilen dik dairesel silindir biçimindeki bir
borunun dolgu kısmının toplam alanını hesaplama.
3. Yanal alanı ile yüksekliği verilen dik dairesel silindirin hacmini ve toplam
alanını bulma.
4.Bir dikdörtgenin kenarları etrafında döndürülmesi ile oluşan silindirin
hacimleri ve alanları arasındaki ilişkiyi bulma.
Amaç-8: Dairesel Koniyi, Alanını ve Hacmini Kavrayabilme.
DAVRANIŞLAR:
1. Koniyi tanımlama.
2. Dik dairesel koniyi tanımlama.
4. Dik dairesel koninin yüksekliğini tanımlama.
5.Dik dairesel koninin ana doğrusunu tanımlama.
7 7.Dik dairesel koninin hacmini veren bağıntıyı yazma.
10. Dik dairesel koninin yanal alanını veren bağıntıyı söyleme ve gösterme.
11. Dik dairesel koninin toplam alanını veren bağıntıyı söyleme ve gösterme.
Amaç-9: Dik Dairesel Koninin Alanı ve Hacmi ile İlgili Uygulama Yapabilme.
DAVRANIŞLAR:
1. Yanal yüksekliği ile tabanının çapı verilen dik dairesel koninin toplam
alanını ve hacmini bulma.
2. Verilen bir dik yamuğun dik kenarı etrafında döndürülmesiyle elde edilen
cismin hacmini ve toplam alanını bulma.
3. Verilen bir yamuğun paralel kenarları etrafında döndürülmesiyle elde
edilen cisimlerin hacimlerini ve toplam alanlarını hesaplama.
Amaç-10: Küreyi, Alanını ve Hacmini Kavrayabilme.
DAVRANIŞLAR:
1.Küreyi tanımlama.
4.Kürenin bir büyük çemberini tanımlama.
7.Kürenin alanını veren bağıntıyı söyleme ve yazma.
8.Kürenin hacmini veren bağıntıyı söyleme ve yazma.
Amaç-11: Kürenin Alanı ve Hacmi ile İlgili Uygulama Yapabilme.
DAVRANIŞLAR:
1. Hacmi alanına sayısal olarak eşit olan kürenin çapını bulma.
2. Verilen bir dik dairesel silindire içten teğet olan bir küre ile silindirin
hacimleri ve alanları arasındaki bağıntıyı gösterme.
3. Yarı çapları verilen iki kürenin alanlarının ve hacimlerinin oranlarını
bulma.
6.BÖLÜM: DÜZLEMDE VEKTÖRLER
Amaç-1: Yönlü Doğru Parçasını ve Vektörü Kavrayabilme.
DAVRANIŞLAR:
1. Yönlü doğru parçasını tanımlama ve sembolle gösterme.
2. Yönlü doğru parçasının uzunluğunu tanımlama ve sembolle gösterme.
3. Yönlü doğru parçasının taşıyıcısını tanımlama.
4. Yönlü doğru parçalarının paralelliğini tanımlama ve sembolle gösterme.
5. Yönlü iki doğru parçasının eşliğini tanımlama ve sembolle gösterme.
6. Düzlemdeki yönlü doğru parçaları kümesinde tanımlanan eşlik bağıntısının bir denklik
bağıntısı olduğunu gösterme.
7. Vektörü tanımlama,
8. Yönlü doğru parçaları ile vektör arasındaki ilişkiyi yazma.
9. Sıfır vektörünü tanımlama.
Amaç-2: Yönlü Doğru Parçaları ile Uygulama Yapabilme.
DAVRANIŞLAR:
1. Verilen bir yönlü doğru parçasının başlangıç noktasını, bitim noktasına
doğrultusunu, yönünü, uzunluğunu belirtme.
2. Verilen bir yönlü doğru parçasının ters yönlüsünü çizme.
8 3. Düzlemde verilen yönlü doğru parçasına, dışındaki bir noktadan eş bir yönlü doğru
parçası çizme.
Amaç-5: Analitik Düzlemde Vektörü Kavrayabilme.
DAVRANIŞLAR:
1. Yer (konum) vektörünü tanımlama.
2. Yer vektörleri ile analitik düzlemin noktaları arasındaki ilişkiyi söyleme.
3. Yer vektörünün bileşenlerini tanımlama ve sembolle gösterme.
4. Vektörü temsil eden yönlü doğru parçasının başlangıç ve bitim noktaları
verildiğinde vektörün bileşenlerini bulma ve bu vektöre eş olan yer vektörü ile ilişkisini
gösterme.
5. Yer vektörünün uzunluğunu bulma.
6. Bir vektörün uzunluğunu bileşenleri cinsinden yazma.
7. Bir vektörün toplamını ve farkını bileşenleri cinsinden bulma.
8. Vektörler kümesinde toplama işleminin özelliklerini bileşenler yardımıyla söyleme ve
gösterme.
9. Bir vektörün bir reel sayı ile çarpımını bileşenleri cinsinden belirleme.
10. Bir vektörün bir reel sayı ile çarpımının özellikleri bileşenleri cinsinden belirleme.
11. Paralel iki vektörün bileşenleri arasındaki ilişkiyi bulma.
Amaç-6: Analitik Düzlemde Vektörlerle İlgili Uygulama Yapabilme.
DAVRANIŞLAR:
1. Verilen bir vektörün bileşenlerinin nasıl bulunacağını açıklama.
2. Bileşenleri ile verilen bir vektörün uzunluğunu bulma.
3. Verilen iki noktanın belirttiği vektörün bileşenlerini bulma.
4. Bileşenleri ile verilen iki vektörün toplamını bulma.
5. Verilen bir vektörün toplama işlemine göre tersini bulma.
6.Sıfırdan farklı olarak verilen iki vektörün paralel olup olmadığını belirleme.
7. Verilen bir vektörün, belirtilen bir reel sayı ile çarpımını bulma.
Amaç-7: Vektörler Kümesinde Vektörlerin Lineer Bileşimini kavrayabilme.
DAVRANIŞLAR:
1. Birim vektörü tanımlama.
2. Bir vektörle aynı yönlü birim vektörü bulma ve yazma.
3. İki vektörün lineer bileşimini tanımlama.
4. İki vektörün lineer bağımlı olmasını tanımlama.
5. İki vektörün lineer bağımsız olmasını tanımlama.
Amaç-8: Vektörler Kümesinde Vektörlerin Lineer Bileşimi ile İlgili Uygulama
Yapabilme.
DAVRANIŞLAR:
1. Bileşenleri ile verilen bir vektörün, birim vektör olup olmadığını söyleme ve yazma.
2. Bileşenleri ile verilen bir vektörü standart taban vektörler kümesi türünden yazma.
3. Bileşenleri ile verilen iki vektörün lineer bağımlı olup olmadığını belirtme.
5.Verilen iki vektörün lineer bağımsız olup olmadığını belirtme.
6.Sıfır vektörünü kapsayacak şekilde verilen her vektör kümesinin lineer bağımlı
olduğunu gösterme.
9 18. GEOMETRİ dersinde; Talim ve Terbiye Kurulu' nun 29.1.1992 tarih ve 14 sayılı kararı ile
kabul edilen Ortaöğretim Geometri 1,2,3 ve Ortaöğretim Analitik Geometri 1,2 dersi öğretim
programlarından,
9. SINIFLARDA;
GEOMETRİ 1 Dersi Öğretim Programından,
GEOMETRİK KAVRAMLAR
Amaç-1/ Davranış-1, 2, 3, 6,7, 8, 9
Amaç-2/ Davranış-1, 2, 3, 4, 5, 6
Amaç-3/ Davranış-1, 2, 3, 4, 5, 6, 7, 8, 9
Amaç-4/ Davranış-1, 2, 3
Amaç-5/ Davranış-1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16
Amaç-6/ Davranış-1, 2, 3, 4, 5
ANALİTİK GEOMETRİ 1 Dersi Öğretim Programından,
DOĞRUNUN ANALİTİK İNCELENMESİ
Amaç-1/ Davranış-1, 2, 3, 4
Amaç-2/ Davranış-1, 2, 4
Amaç-3/ Davranış-1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18
Amaç-4/ Davranış-1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12
GEOMETRİ 1 Dersi Öğretim Programından,
ÜÇGENLER
Amaç-1/ Davranış-1, 2, 3, 4, 9, 10
Amaç-2/ Davranış-1, 3, 4, 5, 6, 7, 8
(Üçgenlerde benzerlik bölümünden )
Amaç-3/ Davranış-1, 2, 3, 4
Amaç-4/ Davranış-1, 2
GEOMETRİ 2 Dersi Öğretim Programından,
ÇEMBER
Amaç-1/ Davranış-1, 2, 3, 4, 5, 6, 7
Amaç-2/ Davranış-1, 2, 3
Amaç-3/ Davranış-1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16
10 Amaç-4/ Davranış-1, 2, 3, 4, 5
GEOMETRİ 3 Dersi Öğretim Programından,
KATI CİSİMLER ALAN VE HACİMLERİ
Amaç-1/ Davranış-1, 2, 3, 4, 5, 6, 11, 13, 14, 15, 16, 17, 18
Amaç-2/ Davranış-1, 3, 4
Amaç-3/ Davranış-1, 2, 3, 4, 5
Amaç-4/ Davranış-1, 2, 3, 4, 7, 8
Amaç-5/ Davranış- 2
Amaç-6/ Davranış-1, 2, 4, 6, 7
Amaç-7/ Davranış-1, 2, 3, 4
Amaç-8/ Davranış-1, 2, 4, 5, 7, 10, 11
Amaç-9/ Davranış-1, 2, 3
Amaç-10/ Davranış-1, 4, 7, 8
Amaç-11/ Davranış-1, 2, 3
ANALİTİK GEOMETRİ 1 Dersi Öğretim Programından,
DÜZLEMDE VEKTÖRLER
Amaç-1/ Davranış-1, 2, 3, 4, 5, 6, 7, 8, 9
Amaç-2/ Davranış-1, 2, 3
Amaç-5/ Davranış-1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
Amaç-6/ Davranış-1, 2, 3, 4, 5, 6, 7
Amaç-7/ Davranış-1, 2, 3, 4, 5
Amaç-8/ Davranış-1, 2, 3, 5, 6
uygulanır.
10. SINIFLARDA; GEOMETRİ 1,
11. SINIFLARDA; GEOMETRİ 2,
12. SINIFLARDA; GEOMETRİ 3
öğretim programları aynen uygulanır.
11