Kopyası vektörler

VEKTÖ
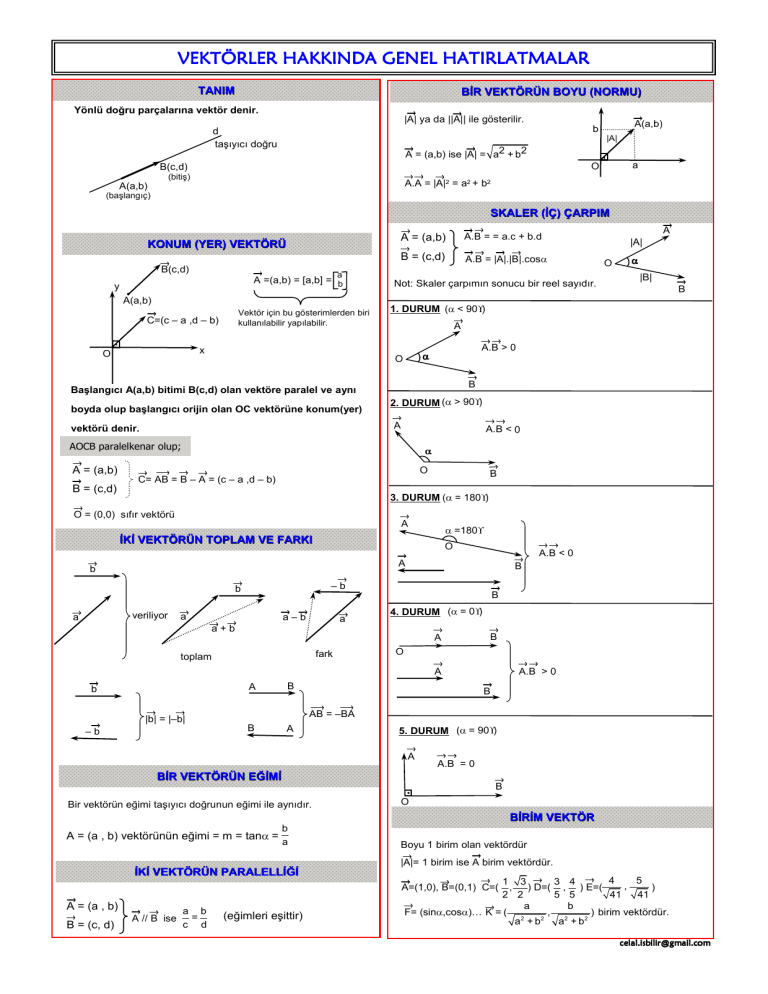
VEKTÖRLER HAKKINDA GENEL HATIRLATMALAR
TANIM
BĐR VEKTÖ
VEKTÖRÜN BOYU (NORMU)
Yönlü doğru parçalarına vektör denir.
|A| ya da ||A|| ile gösterilir.
A(a,b)
b
d
taşıyıcı doğru
|A|
A = (a,b) ise |A| = a2 + b2
.
O
B(c,d)
(bitiş)
a
A.A = |A|2 = a2 + b2
A(a,b)
(başlangıç)
SKALER (Đ
(ĐÇ) ÇARPIM
KONUM (YER) VEKTÖ
VEKTÖRÜ
B(c,d)
y
a
A =(a,b) = [a,b] = b
.
A(a,b)
Vektör için bu gösterimlerden biri
kullanılabilir yapılabilir.
C=(c – a ,d – b)
A = (a,b)
A.B = = a.c + b.d
B = (c,d)
A.B = |A|.|B|.cosα
Not: Skaler çarpımın sonucu bir reel sayıdır.
x
|B|
B
A.B > 0
α
B
Başlangıcı A(a,b) bitimi B(c,d) olan vektöre paralel ve aynı
2. DURUM (α > 90°)
A
vektörü denir.
α
A
O
boyda olup başlangıcı orijin olan OC vektörüne konum(yer)
O
1. DURUM (α < 90°)
.
O
A
|A|
A.B < 0
AOCB paralelkenar olup;
α
A = (a,b)
O
B
C= AB = B – A = (c – a ,d – b)
B = (c,d)
3. DURUM (α = 180°)
O = (0,0) sıfır vektörü
A
α =180°
ĐKĐ VEKTÖ
VEKTÖRÜN TOPLAM VE FARKI
O
b
veriliyor
B
–b
b
a
A.B < 0
A
B
a
a–b
a
4. DURUM (α = 0°)
a+b
A
fark
toplam
B
O
A
A
b
B
B
AB = –BA
|b| = |–b|
B
–b
A.B > 0
A
5. DURUM (α = 90°)
A
BĐR VEKTÖ
MĐ
VEKTÖRÜN EĞĐ
EĞĐM
Bir vektörün eğimi taşıyıcı doğrunun eğimi ile aynıdır.
.
A.B = 0
B
O
BĐRĐM VEKTÖ
VEKTÖR
b
A = (a , b) vektörünün eğimi = m = tanα =
a
Boyu 1 birim olan vektördür
|A|= 1 birim ise A birim vektördür.
ĐKĐ VEKTÖ
VEKTÖRÜN PARALELLĐĞĐ
PARALELLĐĞĐ
4
5
1 3
3 4
,
, ) D=( , ) E=(
)
41
41
2 2
5 5
a
b
F= (sinα,cosα)… K = (
,
) birim vektördür.
a 2 + b2 a2 + b 2
A=(1,0), B=(0,1) C=(
A = (a , b)
B = (c, d)
A // B ise
a b
=
c d
(eğimleri eşittir)
celal.isbilir
celal.isbilir@
[email protected]
gmail.com
DĐK ĐZDÜ
ZDÜŞÜM VEKTÖ
VEKTÖRÜNÜ BULMA
BĐR VEKTÖ
VEKTÖR YÖ
YÖNÜNDEKĐ
NDEKĐ BĐRĐM VEKTÖ
VEKTÖR
A=(a,b) yönündeki birim vektör
a
B=(
2
a +b
2
,
b
2
a +b
OH A vektörünün B
A=(a,b)
2
) vektörüdür
vektörü üzerindeki dik
izdüşüm vektörüdür.
|A|
O
α
.
B
H
|B|
B
B yönündeki birim vektör
olup
|B|
BĐR VEKTÖ
VEKTÖR DOĞ
DOĞRULTUSUNDAKĐ
RULTUSUNDAKĐ BĐRĐM
VEKTÖ
VEKTÖRLER
B
Đzdüşüm vektörü OH =
| OH |
|B|
A=(a,b) doğrultusundaki birim vektörler
B = ±(
a
a2 + b2
,
b
a2 + b2
)
BĐR DOĞ
DOĞRUNUN DOĞ
DOĞRULTMAN VEKTÖ
VEKTÖRLERĐ
RLERĐ
vektörleridir
ax + by + c = 0 doğrusunun doğrultman vektörleri
A=(– b,a) veya B=(b, –a)
TEMEL(BAZ) BĐ
BĐRĐM VEKTÖ
VEKTÖRLER
by+
ax+
A=(– b,a)
e1=(1,0)
Vektörlerine temel (baz ) birim vektörler denir.
c=
0
e2=(0,1)
y
e1= i = (1,0)
e2= j = (0,1)
e1=(0,1)
.
O
e2=(1,0)
B=(b, – a)
Şeklinde de yazılabilir
BĐR DOĞ
DOĞRUYA DĐ
DĐK OLAN VEKTÖ
VEKTÖRLER
x
ax + by + c = 0 doğrusuna dik olan vektörler
A= (a,b) veya
B= (– a, –b)
Temel birim vektörler dışındaki tüm vektörler temel birim
vektörler cinsinden (temel vektörler baz alınarak) yazılabilir.
Yani;
A =(– b,a)
.
A = (a,b) = (a,0) + (0,b) = a.(1,0) + b.(0,1) = a.e1+b.e2
e1
.
c=
by+
ax+
0
B =(b, – a)
e2
A = (a,b) = i.e1 + j.e2
LĐNEER BAĞ
BAĞIMLI VEKTÖ
VEKTÖRLER
|A|
0
| OH | =
.
H
A.B
|B|
a b
=
dir. yani A // B dir.
c d
|OH| A vektörünün B
A(a,b)
α
B = (c,d)
Lineer bağımlı ise
B(c,d)
vektörü üzerindeki dik
I- Lineer bağımlı vektörler bulundukları uzayı germezler.
izdüşüm uzunluğudur.
II- Paralel vektörler bulundukları uzayı germezler.
III- Eğimleri aynı vektörler bulundukları uzayı germezler.
NOT; Bir vektör aynı doğrultuda olmayan herhangi iki
Aynı anlamda 3 cümle
A = (a,b)
DĐK ĐZDÜ
ZDÜŞÜM
vektörün lineer bileşimi olarak yazılabilir
HAZIRLAYAN : [email protected]