det 0 A ≠ det 0

1) Dışardan girilen bir n sayısı için An×n
SORULAR
rasgele matrisini ve bn×1 rasgele vektörürünü (elemanları
− n 2 ile n 2 arasında değişen tamsayılar olarak) üretip Cramer yöntemi ile Ax = b matris
denkleminin ( n bilinmeyenli n denklemden oluşan lineer denklem sistemi) çözümü olan xn×1
vektörünü det ( A) ≠ 0 ise bulduran ve matrisler ile çözüm vektörünü uygun formatta ekrana
yazdıran, det ( A) = 0 ise programın bir daha çalıştırılmasını isteyen program hazırlayınız.
Not:
Cramer yöntemi,
x bilinmeyenler vektörünün her bir elemanı xi ve
A matrisinin i inci sütununun silinip yerine b vektörünün yazılması ile oluşan matris Ai
ile gösterilmek üzere
det ( Ai )
xi =
det ( A )
ile x vektörünün elemanlarını bulan bir yöntemdir.
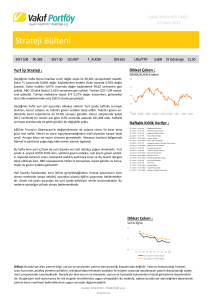
2) Aşağıdaki grafiğin çıkmasını sağlayan editörü hazırlayınız.
3) Bir başlangıç ve bitiş değerini kullanıcıdan alan, bu başlangıç ve bitiş değerleri arasındaki sayılar
için y = x 2 − 3 koşulunun sağlanıp sağlanmadığını kontrol eden; sağlanan sayı buluyorsa bu sayı
ikililerini yazdıran, bulamıyorsa bu aralıkta istenen koşulu sağlayan sayılar yoktur bilgisi veren bir
program hazırlayınız.
4) Bilindiği üzere bir f(x) fonksiyonunun Maclaurin Serisinin genel ifadesi
f ′(0)
f ′′ ( 0 ) 2
f ( x ) = f (0) +
x+
x +⋯
1!
2!
şeklindedir. Dolayısı ile f ( x ) = e x fonksiyonu için bu seri
f ( x ) = ex = 1 +
∞
x x2
xk
+ +⋯ = ∑
1! 2!
k =0 k !
şeklinde olacaktır. Bu seri eğer n inci mertebeye kadar türevleri içerecek şekilde yapılırsa ona n.
mertebeden Maclaurin açılımı denir ve
n
xk
f ( x ) = ex ≅ ∑
k =0 k !
olur. Buna göre kullanıcıdan bir x ve n değeri alıp n inci mertebe Maclaurin açılımı toplamını bulan
ve bunu gerçek e x değeri ile karşılaştıran ve bulduklarını ekrana uygun formatta yazdıran bir
program hazırlayınız.
5) Klavyeden girilen bir h değeri için bir top h metre yüksekten atılıyor. Her defasında %70 i kadar
zıplıyor. 0,00001 metre veya daha az yüksekte ise durdu kabul edilecektir. Toplam kaç kere zıplar?
Durduğunda ne kadar yüksekliktedir?
6) Barındırdığı rakamları toplamına tam olarak bölünebilen sayılara Harshad sayısı denir. Örneğin
24 sayısı rakamları toplamı olan 2+4=6 ya tam olarak bölünür ve bir Harshad Sayısıdır. Buna göre
klavyeden girilen bir sayının Harshad sayısı olup olmadığını belirleyen bir program hazırlayınız.
CEVAPLAR
1)
clear;clc;
n=input('Lineer Denklem sisteminin boyutunu giriniz: ');
A=round(-n^2+2*n^2*rand(n,n))
b=round(-n^2+2*n^2*rand(n,1))
if det(A)~=0
fprintf('Bulunan çözüm vektörü:\n');
fprintf('x= ');
for i=1:n
DegismisA=A;
DegismisA(:,i)=b;
x(i)=det(DegismisA)/det(A);
fprintf('%g ',x(i));
end
fprintf(' dir.\n\n\n');
else
fprintf('Lütfen programı bir daha çalıştırınız.\n');
end
2)
clear;clc;
s(1)=subplot(2,2,1);
s(2)=subplot(2,2,2);
s(3)=subplot(2,2,3);
s(4)=subplot(2,2,4);
[X,Y]=meshgrid(-5:1/5:5 -5:1/5:5)
Z1=X.^3+Y.^4
Z2=sin(X.^2)-Y.^2
mesh(s(1),X,Y,Z1)
title(s(1),'z=x^3+y^4')
xlabel('x')
ylabel('y')
zlabel('z')
mesh(s(2),X,Y,Z2)
title(s(2),'z=-y^2+sinx^2')
xlabel('x')
ylabel('y')
zlabel('z')
x=linspace(-2,2,100)
y=x.^3
plot(s(3),x,y)
title(s(3),'y=x^3')
xlabel('x')
ylabel('y')
t=0:pi/100:10*pi
plot3(s(4),2*cos(t),sin(2*t),5*t.^2)
title(s(4),'x=2cost, y=sin2t, z=5t^2')
xlabel('x')
ylabel('y')
zlabel('z')
3)
%Baslangic ve Bitis değerleri al
%Bu sayılar arasındaki sayı ikilileri için ... koşulunun sağlanıp sağlanmadığını kontrol et
%Her sağlanma işlemi gerçeklendiğinde bu sayıları ekrana yaz
%Eğer hiç sağlayan yoksa böyle sayı ikilisi yok yaz
clear;clc;
a=input('Araya hangi sayıdan başlansın? ');
b=input('Arama hangi sayıda bitirilsin? ');
Toplam=0;
Kontrol=0;
for x=a:b
for y=a:b
if y==x^2-3
fprintf('(%g,%g)\n',x,y);
Kontrol=1;
end
end
end
if Kontrol==0
fprintf('Bu aralıkta koşulu sağlayan sayı yoktur.\n\n');
end
4)
%Klavyeden x ve n sayılarını al
%Toplam değişkenine 0 ata
%k=0 dan 1 er artarak n sayısına gidene kadat ... yı toplam değişkenine ekle
%exp(x) in gerçek ve bulunan değerini karşılararak kullanıcıya yorumla
clear;clc;
x=input('Hangi sayının eksponansiyelini hesaplamak istersiniz? ');
n=input('Açılım kaç terim içersin? ');
Toplam=0;
for k=0:n
Toplam=Toplam+x^k/factorial(k);
end
fprintf('Girdiğiniz x=%g sayısı için %d terimli açılıma göre exp(%g) yaklaşık olarak %g
dir.\n\n',x,n,x,Toplam);
fprintf('Gerçekte exp(%g) değeri %g dir.\n\n',x,exp(x));
fprintf('Dolayısıyla bu açılım %g hatalı sonuç bulmuştur.\n\n',abs(exp(x)-Toplam));
5)
%Klavyeden sayı yüksekliği al
%ziplama değişkenine 0 ata
%Yükseklik 0.00001 veya daha az olana kadar her defasında yüksekliği %70 e
%indir ve ziplama değişkenini 1 artir
%ziplama sayısını ekrana uygun formatta yazdır
clear;clc;
h=input('Lütfen bir yükseklik değeri giriniz: ');
Ziplama=0;
while h>0.00001
Ziplama=Ziplama+1;
h=h*0.7;
end
fprintf('Top toplam %d kez zıplamıştır.\n\n',Ziplama);
6)
%Klavyeden sayı al
%Toplam değişkenine 0 ata
%Sayının her defasında birler basamağını bul ve toplama ekle ayrıca sayının
%birler basamağını sayıdan at
%Oluşan yeni sayı için işleme devam et
%Sayının basamakları toplamı sayıyı tam bölüyorsa 'Harshad sayısıdır'
%Sayının basamakları toplamı sayıyı tam bölümüyorsa 'Harshad sayısı
%değildir'
clear;clc;
Sayi=input('Lütfen bir sayı giriniz: ');
GirilenSayi=Sayi;
Toplam=0;
while Sayi>0
Birler=mod(Sayi,10); %Sayının birler basamağını bulan kod
Toplam=Toplam+Birler;
Sayi=fix(Sayi/10); %Sayinin birler basamağını atan kod
end
if mod(GirilenSayi,Toplam)==0
fprintf('Bu sayı bir Harshad Sayısıdır.\n\n');
else
fprintf('Bu sayı bir Harshad Sayısı değildir.\n\n');
end